梯度域多曝光图像融合*

(中国西南电子技术研究所，成都 610036)

1 引 言

众所周知,普通成像设备是无法捕获场景中的整个亮度动态范围的。即使高端的单反相机具有扩展位宽的记录能力，但是其内部的数字感光器件仍只有有限动态范围的接受能力，这限制了普通消费级别的相机不能在一次曝光中产生真正的高动态范围(High Dynamic Range,HDR)图像[1]。有效的解决办法是利用多张不同曝光的图像融合成高动态范围图像[2]。公认的多曝光图像合成高动态范围图像的过程有3个步骤,即相机的标定、多曝光图像合成、动态范围压缩。遵循这3个传统的步骤，虽然过程清晰、效果好，但是计算太繁琐。首先，相机的标定需要已知相机的一些参数，但是在实际应用中，例如图像是从网上下载的，就无法得知这些参数。另外，多曝光图像合成的目的是为了能够正常显示，第二步得到的高动态范围图像成了中间结果，而最终结果是动态范围压缩的低动态范围(Low Dynamic Range,LDR)图像。因此，本文将讨论如何采用图像融合的方法直接将多曝光图像融合成适合显示的结果图像，以避免繁琐的3个步骤，使计算效率更高，实用性更强。常见的方法是在梯度域融合图像[3]，较像素域加权平均像素值的方法更能突出图像中丰富的边缘和细节信息，更适合人眼观看。本文在梯度域融合多曝光图像的基础上进一步改进算法，使其能够融合含运动景物的图像，消除多曝光图像的不一致处。

在获取多张曝光图像的过程中，有曝光时间和拍摄两幅图像之间的间隔时间，在这段时间内，难免会出现景物移动位置。另一种情况是相机本身有晃动，相机晃动造成图像之间的差别，需要在融合之前对图像进行配准，或者更简单的使用三脚架，消除图像之间的位移。但对于图像内景物的移动，处理更困难。通常的办法是设定标准，选择一幅图像作为参考图像，其他图像中的景物与该参考图像位置有不同，那么在融合中就消除这些不同位置的景物；或者通过估算出相机灰度映射函数(Intensity Mapping Function,IMF)来判断当前像素值是否偏离该映射关系[4],融合时排除那些偏离映射关系的像素值，得到的图像就是一致的，否则,如果不对移动景物采取措施，会得到存在伪影的图像，影响视觉效果，也与真实场景不符。本文采用选择一幅图像作为参考的融合方法，但如何选择参考图像是一件困难的事情，困难在于标准难以确定，或者某些情况下，我们希望结果图像中存在景物在某个位置，但是根据制定的标准而选择的参考图像中，景物却又在另一个位置。针对这个问题，本文提出了一种算法，能够以每一张曝光图像都作为参考图像，分别融合成结果图像，并且结果图像具有相同的高质量，也就是看上去没有曝光的差别。那么对于景物的每一个位置，都有相应的融合图像。

2 算法流程

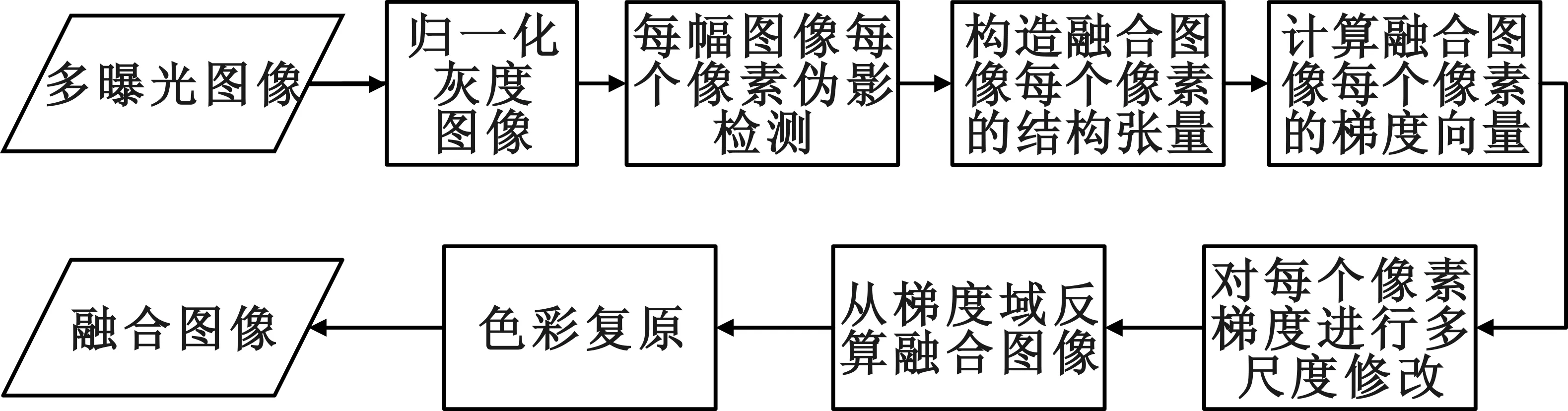
图1 算法流程图Fig.1 The algorithm flow chart

2 基于黎曼几何梯度域融合

一幅HDR图像被看作一个二维曲面，被嵌入到了一个n维空间中。在二维空间中，HDR图像I具有坐标系统(x1,x2)，那么它就是一个黎曼流形，用Ω∈2表示这个二维黎曼流形。HDR图像同样可以用多曝光图像分量表示为(I1,I2,…,In)，每一个分量是一幅曝光图像，同样有坐标系统(x1,x2)，那么在这个n维空间中，HDR图像就被看作是引入了局部坐标系统，因此它也是一个黎曼流形，用M∈n表示。于是就存在一种映射φ:Ω→M，将(Ω,g)嵌入到(M,h)中，其中g和h分别表示各自空间的黎曼度量。

二维空间Ω中HDR图像I的几何性质是由每个像素在各个方向的变化所描述的。首先，每个像素点的全微分可以表示为

(1)

它的平方形式为

(2)

根据映射关系φ，度量g可表示为h的拉回[7]：

g=φ*h=JThJ，

(3)

式中：J是φ的雅可比矩阵：

(4)

通常这个n维特征流形的度量h被假设是欧几里德度量δ，是一个单位矩阵,从而，通过式(3)～(4)就将多幅图像融合得到一个结构张量g。根据公式(2)，g是半正定的，它的最大特征值λ+和特征方向v+，在指定了正负号后，可以构造成一个梯度向量V。通过解如下的泊松方程，得到融合图像f[8]:

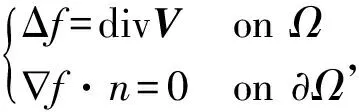
(5)

式中：n是Ω上的单位法向量，∂Ω上的边界条件为诺依曼条件，Δ是拉普拉斯算子，是梯度算子。

3 消除伪影的梯度域融合

由于多幅图像中存在景物运动，造成内容的不一致，直接融合会产生该物体半透明的现象，如图2(f)所示，影响视觉效果。一种简单有效的解决办法是对每幅图像都找到相应的运动物体，在融合过程中消除。

图2 多曝光图像及出现伪影的融合图像Fig.2 Multi-exposure images and their fusion image with ghosts

将式(3)和式(4)合并写为每个像素上的结构张量：

(6)

式中：w是h对角线上的元素。很容易想到，只需要将运动像素位置的w设置为0，其余为1，就可以做到消除运动像素的目的。

3.1 伪影的检测

伪影是由于多幅图像内容不一致造成的，又因为单幅图像相对于自身是一致的[1]，那么选择一幅图像作为参考图像后，就可以选出其他图像的差别之处。但是，这种差别不能用减法来实现，因为所有的像素值在曝光不同的情况下都在变化。理论上，不同曝光图像像素值之间的关系是由如下公式表示的：

Ib=F(Ia)=f(f-1(Ia)·e)。

(7)

式中：f是相机的响应函数，e是与曝光相关的参数。公式(7)表达了像素值之间的关系是通过映射函数F来定义的，其形状可以简单的通过联合直方图估计得到。

联合直方图反映了空间上相应像素的值的概率密度分布，它又是一个矩阵，表示为

对于喂食，如果宝宝已经发出了明显的拒绝信号：不张嘴、扭头等，就应该把他抱下餐椅。这点非常重要，这是在帮宝宝建立良好的用餐习惯，让他知道：吃就在，不吃就要离开。如果你不想两三岁还要每天追在屁股后面喂饭，那么从最开始就应该让孩子知道，这个时间、这个场景，是要来吃饭的。如果不想吃、吃够了，就需要离开，离开之后是不会再吃到食物的。

(8)

式中：Jh就是这个矩阵；M是图像中像素的个数；p是一个像素的位置；T[·]是一个函数，如果括号里面的等式成立，就取值1，否则取值0。联合直方图如图2(g)～(h)所示，图中像素越亮，表示其概率密度越大。

首先假设图像中运动物体所占的面积远远小于背景的面积，一般情况下，这个假设都成立。那么一对图像中大多数相应位置的像素应该符合关系函数F，在联合直方图中，可以通过查找最大概率来确定大多数的像素对应关系。对于图2(g)中竖直方向上搜索找到最大概率的位置，记录下来，描绘如图3(a)所示，这就是函数F形状的估计。为了获得F更准确的估计，需要将其平滑，并且使得它单调递增。在搜索像素对的过程中，采用了三步操作：首先，设置了一个阈值，那些概率低于10-5的像素对被去除；其次，相邻位置Ib的增量不能大于20，如果超过了这个阈值，就强制将增量设置为1；最后，如果Ib在减小，或者增量为负，就设置增量为0。获得的F的估计显示于图3(b)中的蓝色线，而红色线是对反函数F-1的估计。上述两个阈值的精确值很难确定，因此它们被设置得很宽松，设置这两个值是要消除那些明显的错误。

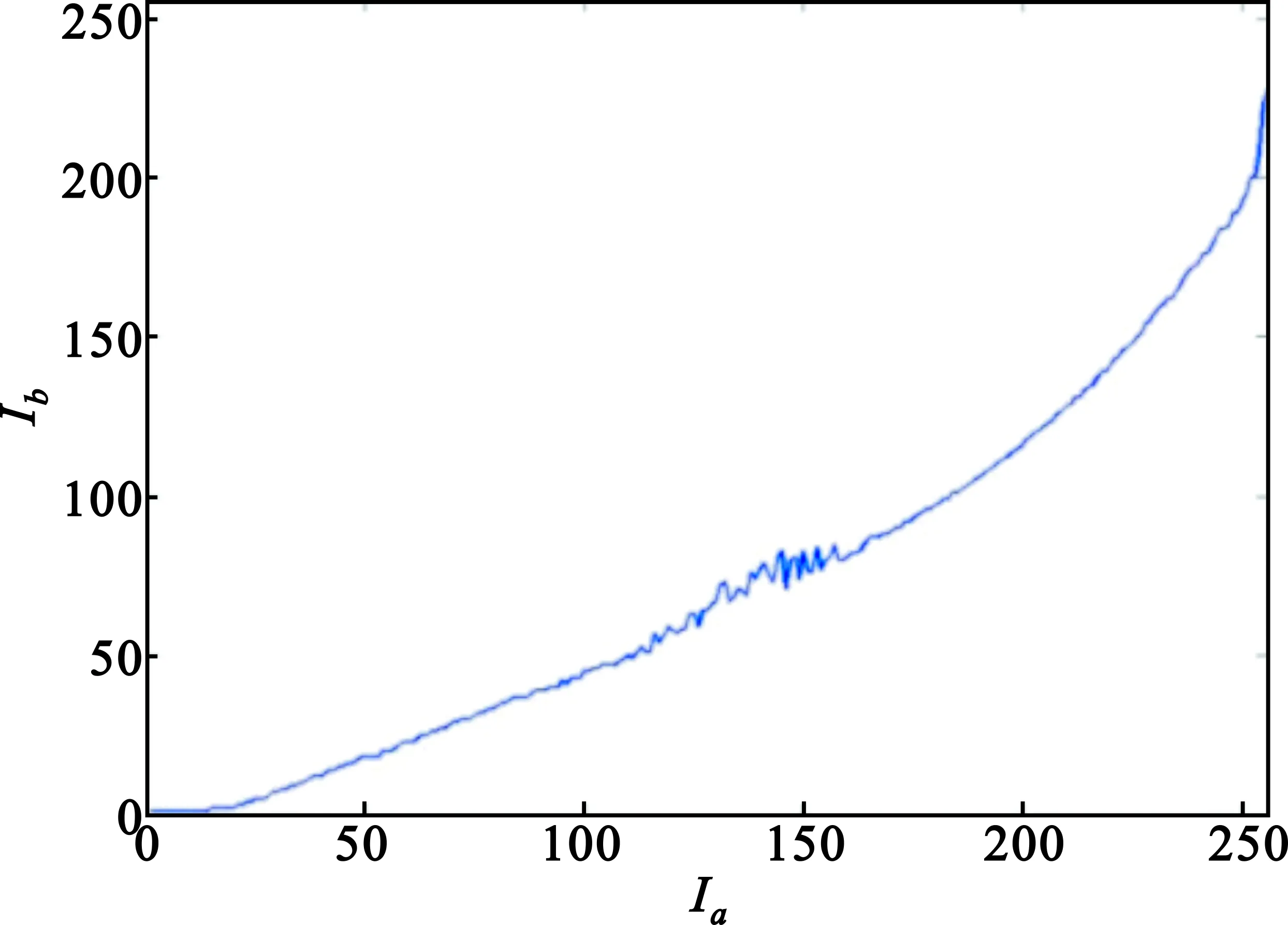
(a)对每一个Ia，具有最大概率的像素对图示

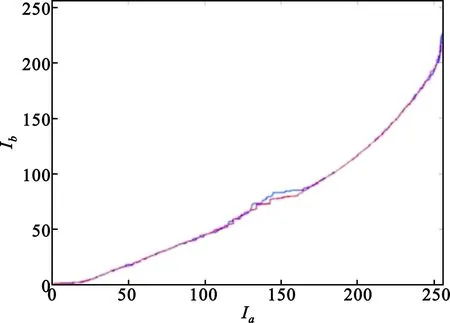
(b)对图(a)的改善图3 多曝光图像间像素值映射关系曲线Fig.3 The mapping curve between pixels in multi-exposure images

因为函数F的输入值是离散的，输出值Ib很可能没有包含所有的像素值。通常的做法是对Ib进行插值，但是插值的方法在这里可能会扩大估计的误差。一种更实用的方法是获取函数F的逆函数：

Ia=F-1(Ib)。

(9)

过程与前面相同，除了它是在图2(g)的水平方向上搜索。获得的F-1估计显示于图3(b)的红色线。这两条线几乎完全一致，这也说明了该估计算法是有效的。

由此建立了任意两张图像的映射关系，如果某像素值违反了这种映射关系，就被认为是伪影像素。许多算法[9-11]提出要选取最佳曝光图像作为参考图像，但是本算法可以选取任意图像作为参考图像，并且结果图像具有相同的高质量，因此更具有鲁棒性。对图2(a)～(e)检测到的伪影区域显示于图4中，图2(c)被选作参考图像。

图4 多曝光图像伪影图Fig.4 The ghost maps of multi-exposure images

3.2 融合算法

为消除伪影，简单的办法是设置式(6)中的融合权值w为0。得到的结构张量g，如第2节所述，可以分解构成梯度向量V：

(10)

3.3 梯度域动态范围压缩

由以上步骤得到的融合图像是HDR图像，不适合正常显示，还需要将它压缩成LDR图像。采用一种直接对梯度进行修改的方法[3]，在多尺度上削减梯度大小来达到压缩动态范围的目的。但是并不像通常的方法那样构造多分辨序列，所有的操作都是在全分辨下完成的，运算效率非常高。

梯度大小可以表示为|V|=|Vx1|+|Vx2|，削减梯度大小的操作在这两个分量独立进行：

(11)

高尺度的梯度从上次修改后的梯度得到：

(12)

式中：N=2l+1，l表示尺度，Avg是均值滤波核，上标T表示转置，*表示卷积运算。

通过迭代运算式(11)和式(12)实现多尺度梯度修改,其中，l=1,2,…,9表示使用了9个尺度。最后解泊松方程(5)，得到融合的LDR图像。图2(a)～(e)的融合图像显示于图5(a)，其中图2(c)被选作参考图像。可以看到，融合图像中没有伪影出现。到目前为止，所有操作都是在图像亮度分量上进行的，下一节将讨论如何恢复色彩信息。

图5 多曝光图像融合结果Fig.5 The fused result of multi-exposure images

4 色彩复原

4.1 色彩的融合

图像的色彩信息是在每个像素上简单地通过输入图像的加权平均得到的。RGB图像的色彩分量是高度相关的，如果每个分量分别采用不同操作，那么很容易造成色彩偏差。因此，对于每个像素的3个色彩分量，它们的权值是相等的。权值计算为

(13)

式中：ω表示权值，Ik是第k幅曝光图像的亮度通道值。ε是一个很小的数，它使得ω非奇，Ik在[0,1]范围上。

色彩融合同样需要避免伪影。在融合计算中，同样使用前面得到的伪影检测图来作为权值。融合色彩图计算为

(14)

式中：C=R,G,B表示输出的3个色彩分类;Cin表示输入;伪影点m=0，其他情况下m=1。

4.2 对融合图像的色彩复原

Fattal等人[12]提出了一种色彩复原的方法，根据每个色彩分量与亮度值的原始比值来恢复色彩值。色彩的复原计算为

(15)

用上式的色彩复原方法会在图像亮度取值范围的高端和低端出现色彩异常。因为在受运动伪影影响的区域中使用了没曝光好的图像信息来融合，然后出现的色彩异常会被式(15)放大。例如，让C等于(1，2，3)表示一个曝光不好区域中记录的像素色彩，这时色彩的偏差还看不出来，因为它几乎是黑色的。如果压缩后的LDR图像的灰度值f=10，并且让β=1，那么计算的输出Cout将等于(25，50，75),这时色彩的偏差就很明显了。

为了控制色彩偏差放大的程度，一种有效的途径是分别用减法和加法来替代除法和乘法。矫正后的色彩复原计算为

Cout=(C-Y)β+f。

(16)

这时，前面所述例子的输出Cout就等于(49，50,51),3个分量之间的差距被保持住了。这个像素呈现灰色，色彩上的偏差仍然保持看不出来。

5 实验结果及分析

图6和图7显示了存在运动物体的不同场景的多曝光图像的融合实验结果。所有实验中，色彩复原使用的参数β都设置为0.7。

图6 与其他算法融合结果对比Fig.6 Results comparison with other methods

图7 分别以图2(a)～(e)作为参考图像得到的融合结果Fig.7 The result images taking Fig. 2(a)～(e) as references respectively

图6显示了本文的结果与其他两种算法[10-11]的对比。Heo[10]同样采用选取参考图的方法，使用联合柱状图设置阈值来选取候选伪影像素点，再使用了一个最小能量方法来提炼和改善伪影区域。本文提出的算法在伪影区域检测之前就要改善像素值映射曲线，避免了耗时的最小能量计算，更重要的是，检测错误会在梯度域融合中得到容忍。Gallo[11]提出选取最佳曝光图像作为参考图，然后将图像进行分块融合。本文方法可以选取任意图像作为参考图，避免了“最佳曝光图像”的定义不明确性。本文结果图6(c)中的天花板看起来要比(b)清楚得多，(c)中的地板砖的纹路、颜色等细节看起来都要比(a)清楚得多。可以说本文算法的结果能清楚地呈现场景中的所有细节，每个位置显示出具有最好的曝光。

本算法的先进之处在于，无论选取哪张源图像作为参考图像，都能获得相同高质量的结果图像，这一点显示于图7中，除了有无运动物体的差别，这些结果图像几乎完全相同。在实际操作中，每张曝光图像都有可能包含我们想要的运动物体，另一方面，要自动或手动地确定一张最佳图像作为参考图像也不是件容易的事情。因此，本算法具有鲁棒性，无论哪幅图像都可以作为参考图像，都能够有效得到高质量的结果。

本算法比Heo等人[10]的方法更有效率，未优化的Matlab程序在装有Intel 3.4 GHz频率CPU的PC条件下处理这些图像中的一幅大约需要20 s，而Heo等人实现其算法的[10]C++程序在相同PC条件下却需要花费6.5 min。

6 结束语

本文提出了一种新颖的融合多曝光动态图像的方法。与现有文献中在像素域选择特定参考图像的融合方法不同，本方法在梯度域融合图像可以选取任意图像作为参考图像，并准确地检测每张图像中运动物体，在融合过程中将其有效移除。本算法实用性较好，使用时所有参数设置为默认值，任意选择一幅图像作为参考图像，都能自动地将输入图像序列转化成一张效果较好的结果LDR图像输出。实验显示结果图像具有较好的质量，适合显示和观看，具备输入图像中所有曝光较好区域的细节信息。

选择参考图像的方法固有一种限制，那些与背景对比度较大的景物容易检测到，而那些与背景相似的景物却难以准确地检测到。进一步可以研究一种不需要选择参考图的方法，认为多幅图像中一致区域的概率较大，而运动区域的概率较小，迭代选取概率较大的区域得到融合图像。这样做的好处是，即使所有图像中都存在运动物体，结果图像中也可以完全消除该物体，而选取参考图像的方法就做不到。如何做到多曝光图像融合达到一致性，目前尚未出现理论和实际应用公认的最佳方法，未来仍然会是高动态范围图像处理领域的重要研究方向。

：

[1] REINHARD E,WARD G,PATTANAIK S,et al.High dynamic range imaging:acquisition,display,and image-based lighting[M].2nd ed. Burlington,MA,USA:Morgan Kaufmann,2010.

[2] DEBEVEC P,MALIK J.Recovering high dynamic range radiance maps from photographs[C]//Proceedings of 1997 International Conference on Computer Graphics and Interactive Techniques.Los Angeles,CA,USA:IEEE,1997:369-378.

[3] GU B,LI W,WONG J,et al.Gradient field multi-exposure images fusion for high dynamic range image visualization[J].Journal of Visual Communication and Image Rrepresentation,2012,23(4):604-610.

[4] MA K,LI H,YONG H,et al.Robust multi-exposure image fusion:a structural patch decomposition approach[J].IEEE Transactions on Image Processing,2017,26(5):2519-2532.

[5] ZENZO S. A note on the gradient of a multi-image[J].Computer Vision,Graphics,and Image Processing,1986,33(1):116-125.

[6] CUMANI A. Edge detection in multispectral images[J].Graphical Models and Image Processing,1991，53(1):40-51.

[7] SOCHEN N,KIMMEL R,MALLADI R. A general framework for low level vision[J].IEEE Transactions on Image Processing,1998,7(3):310-318.

[8] SOCOLINSKY D. A variational approach to image fusion[D].Washington DC:The Johns Hopkins University,2000.

[9] GROSCH T. Fast and robust high dynamic range image generation with camera and object movement[C]//Proceeding of 2006 Vision,Modeling and Visualization Conference. Aachen,Germany:IEEE,2006:277-284.

[10] HEO Y,LEE K,LEE S,et al.Ghost-free high dynamic range imaging[C]//Proceedings of 2010 Asian Conference on Computer Vision(ACCV). Heidelberg，Berlin:Springer,2010:486-500.

[11] GALLO O,GELFAND N,CHEN W,et al.Artifact-free High dynamic range imaging[C]//Proceeding of 2009 IEEE International Conference on Computational Photography(ICCP). Houston,TX:IEEE,2009:1-7.

[12] FATTAL R,LISCHINSKI D,WERMAN M.Gradient domain high dynamic range compression[J].ACM Transactions on Graphics,2002,21(3):249-256.