乘积型指数滤波器及其在多目标时延估计中的应用*
张 路a,季袁冬**
(四川大学 a.数学学院;b.空天科学与工程学院,成都 610065)
1 引 言
时延估计在目标定位、声呐、雷达、地震学、通信系统同步和生物医学工程等方面有着广泛的应用[1-3]。传统的雷达系统通常采用经典的保证最大输出信噪比的匹配滤波器实现目标的时延参数估计[4-5],但是在多目标环境下,利用传统的匹配滤波器的目标时延分辨力较低。
目前,较常用的时延估计改进算法主要有多重信号分类算法[6]和谱估计算法[7],这两类算法在低信噪比情况下容易产生大量的虚假目标。而极大似然估计算法[8]可在高信噪比时逼近克拉美罗界,在低信噪比情况下也具有很好的性能,但其运算涉及搜索算法,计算量较大从而很难直接应用。在匹配滤波器的启发下,文献[9-10]构造了一种具有可变指数的指数滤波器Ha,其指数a∈[-1,1]。匹配滤波器作为其指数a=1的特例,在具有单目标最大输出信噪比的同时具有最低的目标分辨力。指数a<1的指数滤波器则可根据具体情况在充分保证输出信噪比的情况下,产生高于匹配滤波器的目标分辨力,从而实现更高的目标参数估计精度。但是,仅仅采用单个指数滤波器进行多目标时延估计时仍存在输出信噪比和目标时延分辨力均达不到实际需求的情况。
另一方面,针对多项式相位信号,文献[11]提出了一种高阶模糊函数对高阶多项式相位信号进行降级处理,从而实现了多项式相位信号的参数估计。但是由于引入了非线性变换,高阶模糊函数的参数估计性能会随着输入信噪比的降低而快速下降,同时,单个高阶模糊函数在处理多分量多项式相位信号的输出时会出现交叉项干扰引起的较高旁瓣[12]。针对此问题,文献[13-14]又提出将不同阶数的高阶模糊函数相乘得到乘积型高阶模糊函数或改进的乘积型高阶模糊函数,从而在弱化了交叉项的同时增强了自身,进一步抑制了时延旁瓣。
在乘积型高阶模糊函数乘积运算的启发下,本文在指数滤波器的基础上,融合多个指数滤波器分别在输出信噪比和目标分辨力上的优点,构造了一个新的多目标参数估计滤波器——乘积型指数滤波器。该滤波器可以保证较高的单目标输出信噪比,还具有较单个指数滤波器更高的目标时延分辨力。特别地,如果将乘积型指数滤波器中的一个指数滤波器取为匹配滤波器,那么该滤波器较之传统的匹配滤波器具有更理想的多目标时延估计精度,算法主要基于快速傅里叶变换和乘积运算,因此易于实现。
2 信号模型与指数滤波器
设雷达发射的参考信号为r(t),其Fourier变换为R(ω)(幅度|R(ω)|,相位φR(ω)),那么叠加有噪声的K个静止点目标的接收信号可以表示为[3]
(1)
式中:ck和τk分别表示第k个目标的散射系数和时延,n(t)是均值为零、方差为σ的高斯白噪声。
雷达接收机通常采用一个频率响应为H(ω)的线性滤波器处理接收信号,为保证最优的检测和参数估计性能,需要单目标接收信号经过线性滤波器的输出信噪比[9]最大化,这通常是由经典的匹配滤波器实现的[4];另一方面,也需要输出响应的目标分辨力常数最大化[9,15]。事实上,采用逆滤波器可实现目标分辨力常数最大化[9],但是,逆滤波器的输出信噪比较之匹配滤波器的输出信噪比大大恶化[16]。在匹配滤波器和逆滤波器的启发下,文献[9]将雷达接收机线性滤波器的频率响应推广到更一般的形式:
Ha(ω)=|R(ω)|ae-jφR(ω),
(2)
得到指数为a的指数滤波器,a∈[-1,1]。指数滤波器的输出响应在τ=0处取到最大值,其输出信噪比SNR(a)在区间[-1,1]上为增函数,目标分辨力ISL(a)在区间[-1,1]上为减函数。
3 乘积型指数滤波器及其性能分析
3.1 乘积型指数滤波器
从指数滤波器的性质可以看到,单一的指数滤波器无法同时实现输出信噪比和目标分辨力的最优化,如果能将多个指数滤波器进行融合将有望实现比单一指数滤波器更优的目标参数估计性能。事实上,借用乘积型高阶模糊函数[13,17]的思想,本文将多个指数器并联后再串联一个乘法器从而得到乘积型指数滤波器,可以证明其输出幅度平方仍然可以对多目标接收信号实现时延估计,同时由于乘积运算可在弱化旁瓣等杂项的同时增强自项,因此可进一步提高分辨力抑制噪声。
设有N个指数滤波器Hi,i=1,2,…,N,多目标接收信号为x(t),第i个指数滤波器的频率响应为Hi(ω),对x(t)的输出响应为
(3)
式中:ri(t)是指数滤波器Hi对参考信号r(t)的输出响应,ni(t)是Hi对高斯白噪声n(t)的输出响应。则乘积型指滤波器的输出为
(4)
在本文中,将N取定为2。在单目标情况下,两个指数滤波器构成的乘积型指数滤波器的输出为

c1r2(t-τ1)n1(t)+c1r1(t-τ1)n2(t)+
n1(t)n2(t)。
(5)
若没有噪声存在,因为|r1(t-τ1)|、|r2(t-τ1)|均在t=τ1处取得最大值,因此|Y(t)|也在t=τ1处取得最大值,因此最终可以通过对乘积型指数滤波器输出的模进行极大值搜索来实现对多目标时延参数的估计。
3.2 乘积型指数滤波器性能分析
首先假设指数分别为a1和a2的指数滤波器分别对参考信号r(t)的响应为r1(t)和r2(t),这两个指数滤波器构成的乘积型指数滤波器对参考信号r(t)的响应为Y(t)=r1(t)r2(t)。由于|r1(t)|和|r2(t)|均在t=0处取得最大值,则|Y(t)|=|r1(t)||r2(t)|也将在t=0处取得最大值,类似地,它的目标时延分辨力可以定义为
(6)
由于
(7)
因此,ISL12>ISL(a1),同理得ISL12>ISL(a2)。可见乘积型指数滤波器的目标分辨力高于单个指数滤波器的目标分辨力。图1给出了当参考信号为一段相位编码信号时,匹配滤波器、指数为0的指数滤波器以及相应的乘积型指数滤波器对此参考信号的输出响应的归一化模。其中,相位编码采用13位巴克码[1,1,1,1,1,-1,-1,1,1,-1,1,-1,1],采样间隔Δt=10-2μs,采样时长T=2 000Δt。从图1可以看到,乘积型指数滤波器具有更尖锐的主峰和更低的旁瓣。

(a)匹配滤波器
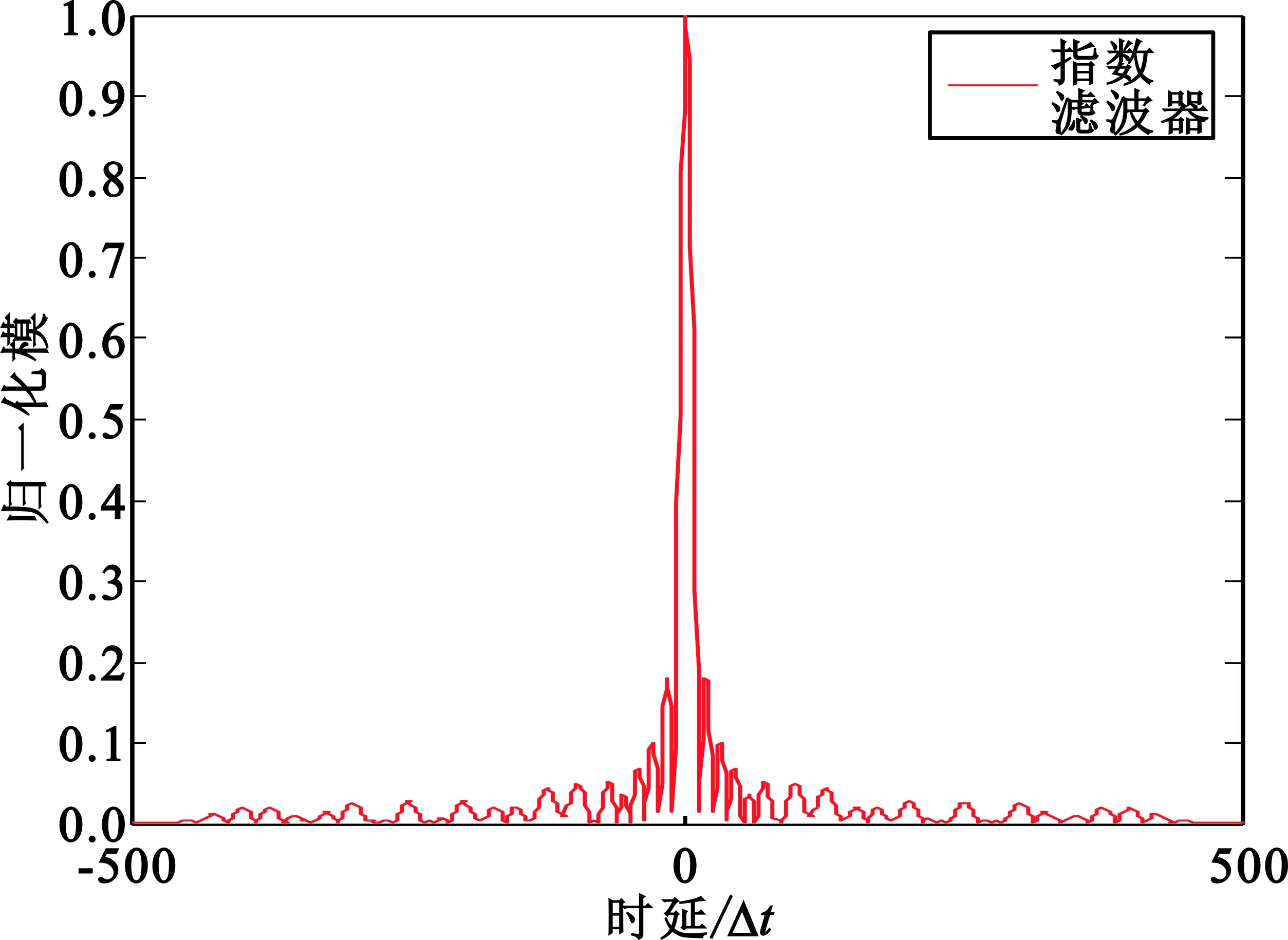
(b)指数为0的指数滤波器
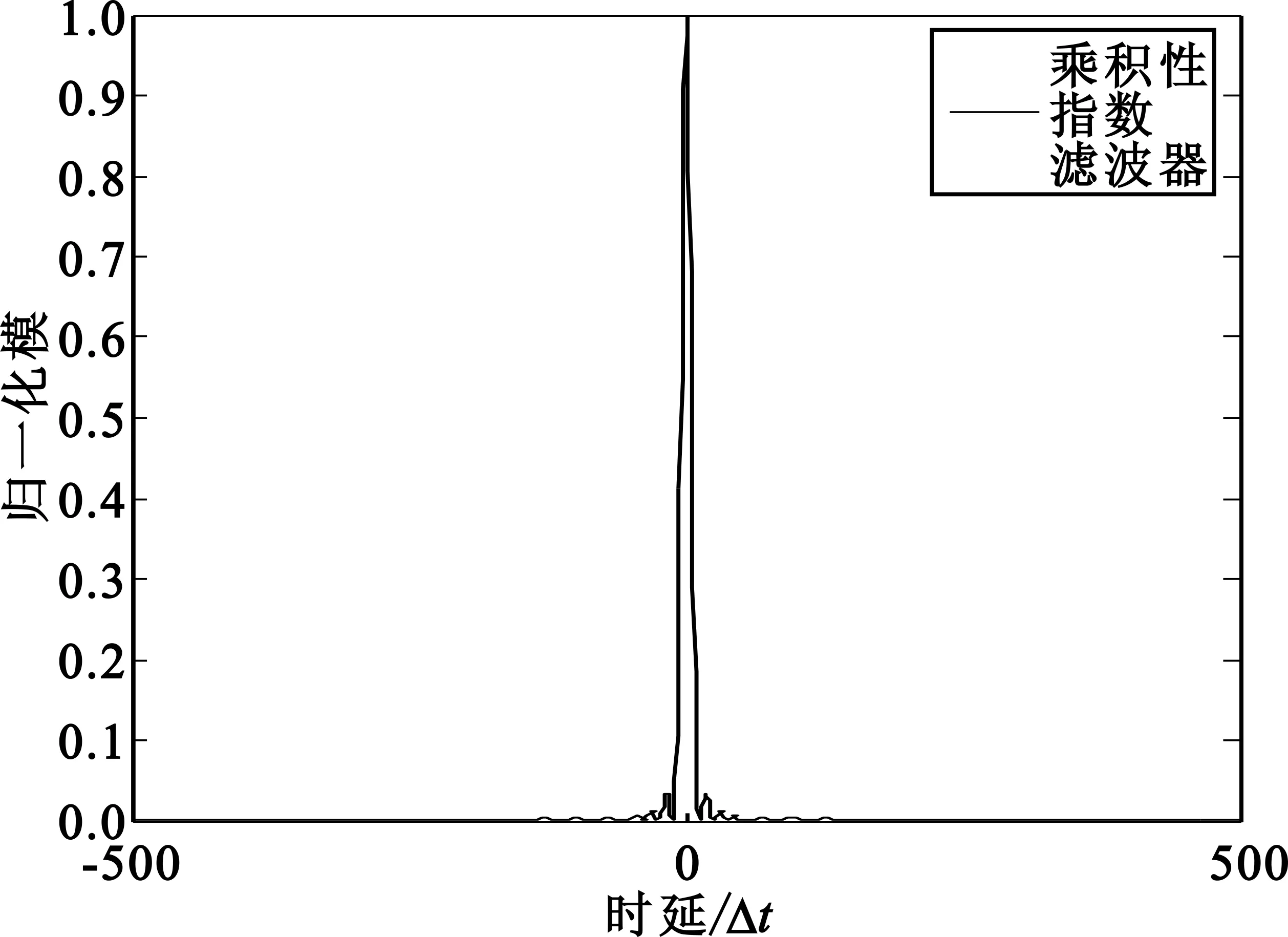
(c)乘积型指数滤波器图1 三种滤波器输出响应的归一化模Fig.1 Normalized modules for the output response of the three filters
在噪声存在的情况下,指数分别为a1和a2的指数滤波器分别对接收信号s(t)=r(t)+n(t)的响应为yn1(t)=r1(t)+n1(t)和yn2(t)=r2(t)+n2(t),这两个指数滤波器构成的乘积型指数滤波器对参考信号s(t)的响应为Yn(t),则有
Yn(t)=yn1(t)yn2(t)=r1(t)r2(t)+r2(t)n1(t)+
r1(t)n2(t)+n1(t)n2(t) 。
(8)
因此,在乘积型指数滤波器的输出Yn(t)中,信号为Y(t)=r1(t)r2(t),噪声为
N(t)=r2(t)n1(t)+r1(t)n2(t)+n1(t)n2(t) 。
(9)
于是输出信噪比可定义为
(10)
当参考信号设置为图1中的相位编码信号时,图2利用数值仿真给出了单个指数滤波器输出信噪比和乘积型指数滤波器的输出信噪比的比较结果。图2(a)给出了当输入信噪比在-10~10 dB之间变化时,匹配滤波器、指数为a=0的指数滤波器以及由匹配滤波器和该指数滤波器得到的乘积型指数滤波器的输出信噪比随着输入信噪比变化的曲线图,可以看到,指数滤波器的输出信噪比较匹配滤波器低8 dB,而乘积型指数滤波器较匹配滤波器的输出信噪比则有7.5 dB左右的提高。图2(b)给出了输入信噪比固定为0 dB时,匹配滤波器、指数为a的指数滤波器以及相应的乘积型指数滤波器的输出信噪比随着指数a变化的曲线图,可以看到,匹配滤波器的输出信噪比为10 dB;指数滤波器的输出信噪比随着指数a的增加而不断增加并逐渐平缓地趋于匹配滤波器(a=1)输出信噪比,这和前面给出结论一致;相应地,乘积型指数滤波器的输出信噪比在指数a较小时低于匹配滤波器输出信噪比;随着指数的不断增加,乘积型指数滤波器的输出信噪比逐渐增加,当a>-0.1时,则超过了匹配滤波器的输出信噪比。
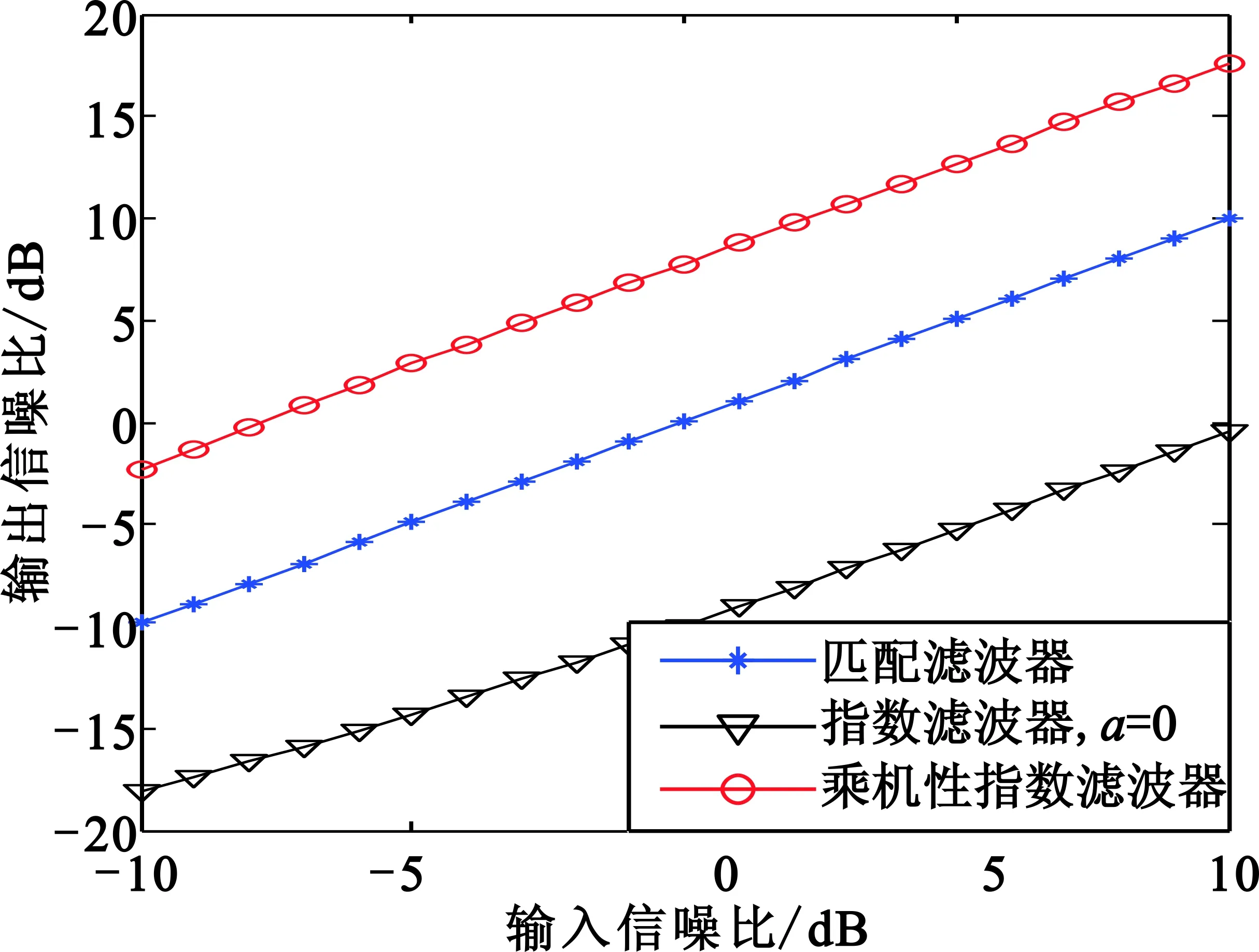
(a)三种滤波器输出信噪比
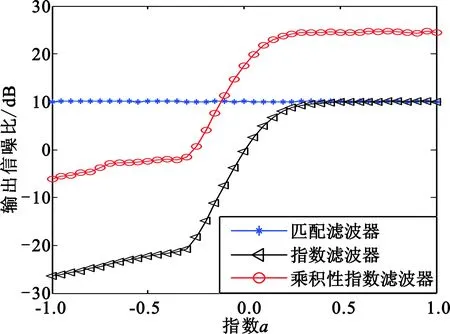
(b)指数滤波器输出信噪比随指数变化的曲线图2 输出信噪比比较Fig.2 Comparison of output SNR
从上面的讨论可以看到,乘积型指数滤波器具有比单个指数滤波器更优的输出信噪比和目标时延分辨力,但是在多目标情况下由于乘法运算将不可避免地引入交叉项,比如,本文考虑具有两个目标的带噪声回波信号s(t)=c1r(t-τ1)+c2r(t-τ2)+n(t),指数分别为a1和a2的指数滤波器分别对接收信号s(t)的响应为yn1(t)=c1r1(t-τ1)+c2r1(t-τ2)+n1(t)和yn2(t)=c1r2(t-τ1)+c2r2(t-τ2)+n2(t),这两个指数滤波器构成的乘积型指数滤波器对参考信号s(t)的响应为Yn(t),则有
Yn(t)=yn1(t)yn2(t)=
|c1|r1(t-τ1)r2(t-τ1)+|c2|2r1(t-τ2)r2(t-τ2)+
c1c2[r1(t-τ2)r2(t-τ1)+r1(t-τ1)r2(t-τ2)]+
[c1r2(t-τ1)+c2r2(t-τ2)]n1(t)+
[c1r1(t-τ1)+c2r1(t-τ2)]n2(t)+n1(t)n2(t)。
(11)
可见乘积型指数滤波器的输出引入了交叉项c1c2[r1(t-τ2)r2(t-τ1)+r1(t-τ1)r2(t-τ2)],由于这一项的存在可能导致输出旁瓣的增加或主瓣的展宽,因此乘积型指数滤波器的性能不能简单地看成优于单个指数滤波器,它应该是一般指数滤波器和匹配滤波器的折中处理器,在一定信噪比情况下会实现比单个指数滤波器以及匹配滤波器更优的参数估计性能。
4 多目标时延估计算法
结合前面的分析推导,下面给出基于乘积型指数滤波器的多目标时延估计算法的具体步骤:
Step1 将接收信号输入匹配滤波器和指数为a的指数滤波器中,得到输出信号。
Step2 将指数滤波器和匹配滤波器的输出输入乘法器,得到乘积型指数阶滤波器的输出。
Step3 对乘积型指数阶滤波器输出的模进行极大值搜索,依次得到各个目标的时延估计量。
5 仿真结果及分析
5.1 仿真实验1
下面的仿真实验中,选定图1中的相位编码信号作为参考信号,利用匹配滤波器和指数为a的指数滤波器构成乘积型指数滤波器来实现具有两个目标的带噪声回波信号的时延参数估计,并将其结果与传统的匹配滤波器以及单个的指数滤波器进行比较。其中,一强一弱两个相邻目标的时延参数分别为τ1=100、τ2=117,单位为采样间隔Δt=10-2μs,散射系数分别为c1=1、c2=0.88,输入信噪比0 dB。图3给出了匹配滤波器、指数为a=0的指数滤波器以及相应的乘积型指数滤波器对此接收信号的响应的归一化模,可以看到,匹配滤波器只检测到了最大的目标,而指数滤波器检测到了两个目标,对两个目标时延估计误差分别为1、0(单位同上);乘积型指数滤波器也检测到了两个目标,对两个目标时延估计误差分别为1、0。
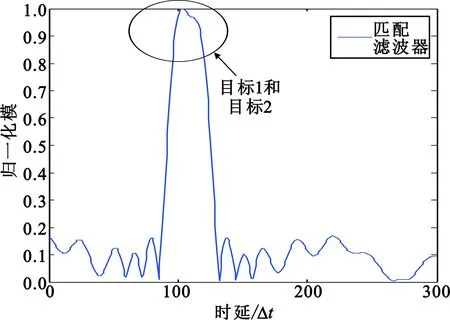
(a)匹配滤波器
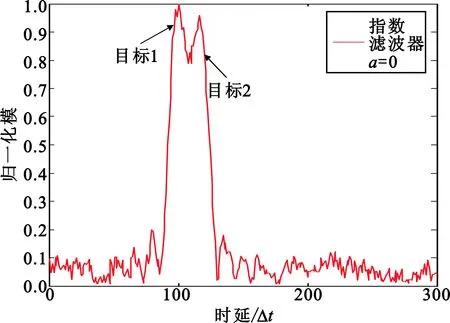
(b)指数a=0的指数滤波器
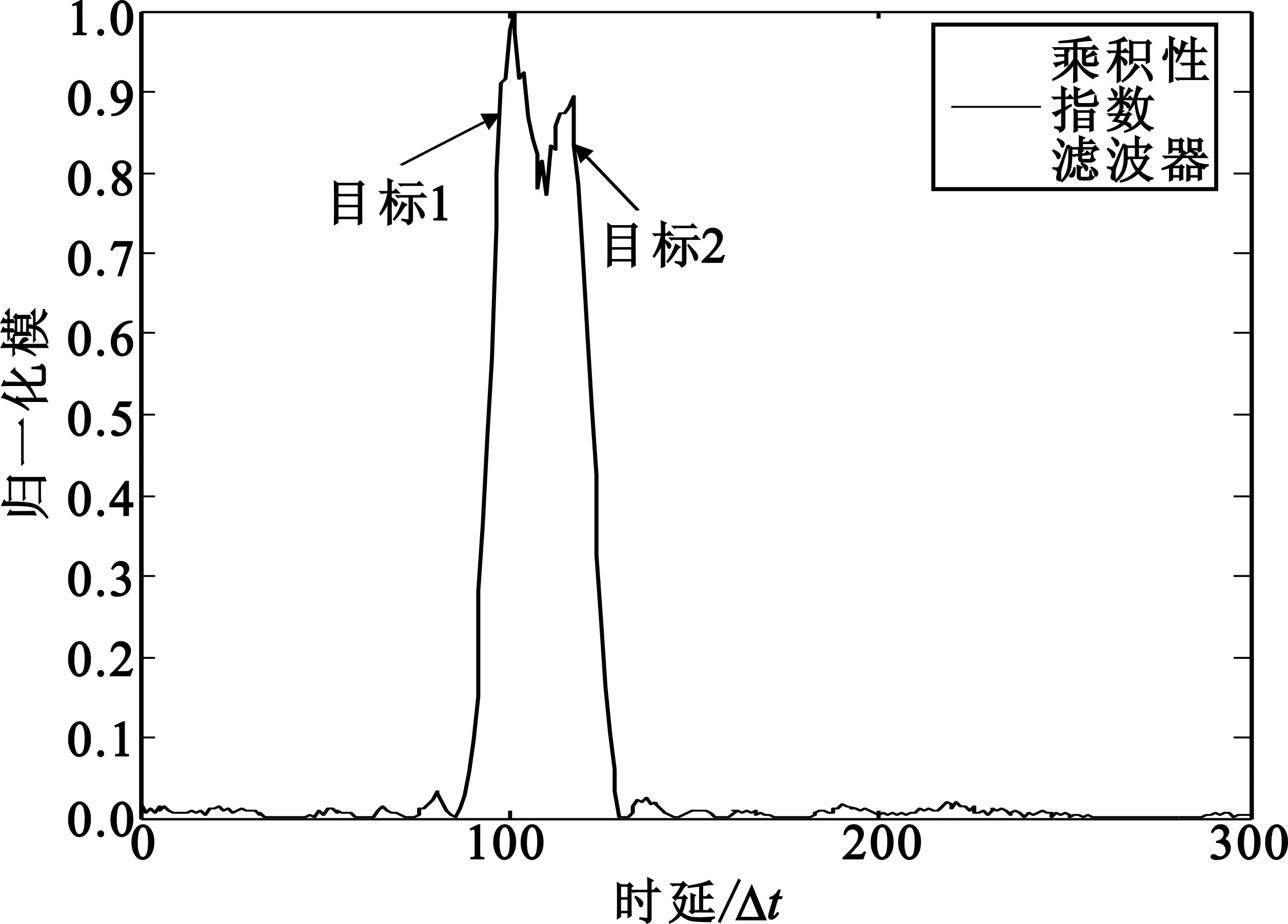
(c)乘积型指数滤波器图3 参考信号为相位编码信号时三种滤波器对两目标接收信号输出响应的归一化模Fig.3 Normalized modules for the output response of the three filters when the reference signal is a phase coded signal
让输入信噪比在[-10,10] dB内变化,图4给出了三种滤波器对最大目标时延估计的均方差误差随着输入信噪比变化的曲线图,其中数值仿真平均次数为5 000次。可以看到,在低信噪比区域([-10,-2] dB),具有最大输出信噪比的匹配滤波器有最低的估计误差;随着信噪比的增加,在中等信噪比区域([-2,5] dB),乘积型指数滤波器具有最低的估计误差,这是因为乘积型指数滤波器较之指数滤波器有更高的输出信噪比,较之匹配滤波器有更高的分辨力,但是由于乘积型指数滤波器交叉项的存在导致其在高信噪比区域([5,10] dB)的估计误差高于指数滤波器。由此可见,乘积型指数滤波器作为匹配滤波器和指数小于1的指数滤波器的折中滤波器,在中等信噪比区域有最低的时延估计误差。
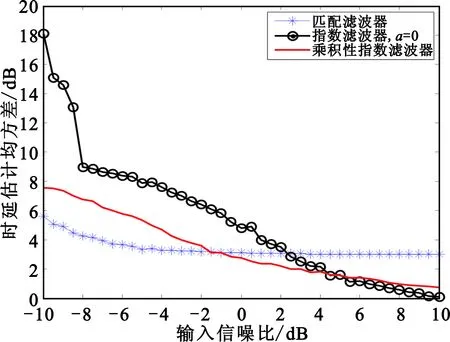
图4 参考信号为相位编码信号时三种滤波器时延估计均方差误差(指数a=0)Fig.4 Mean variance errors of delays of the three filters(a=0) when the reference signal is a phase coded signal
5.2 仿真实验2
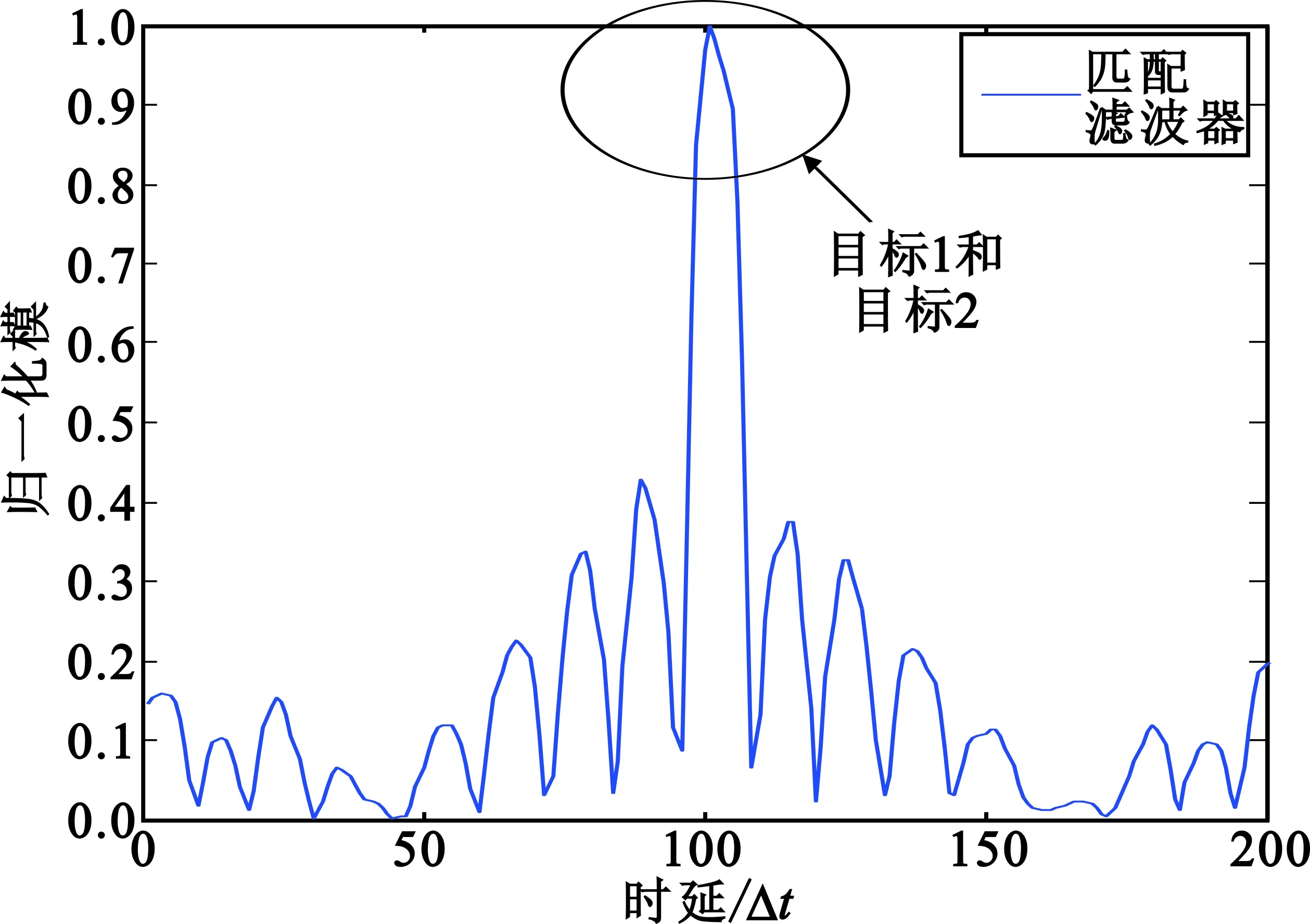
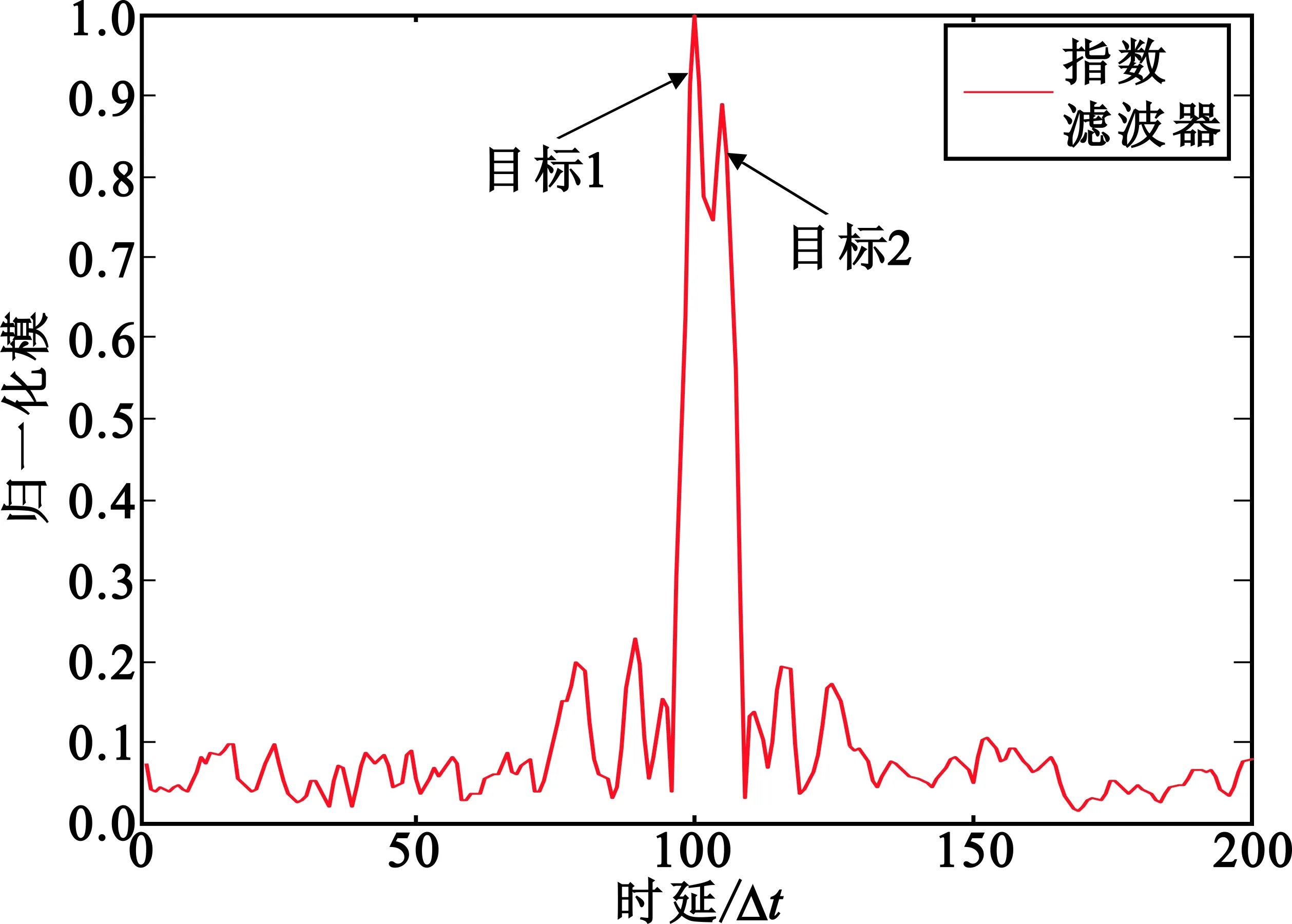
下面的仿真实验中,选定一段FM调频广播信号(带宽5 kHz,采样间隔Δt=10-5s,采样时长T=2 000Δt),利用匹配滤波器和指数为a=0的指数滤波器构成乘积型指数滤波器来实现具有两个目标的带噪声回波信号的时延参数估计,并将其结果与传统的匹配滤波器以及单个的指数滤波器进行比较。其中,一强一弱两个相邻两个目标的时延参数设置为τ1=100、τ2=105,单位为采样间隔Δt=10-5s,散射系数分别为c1=1、c2=0.9,输入信噪比-5 dB。图5分别给出了匹配滤波器、指数为a=0的指数滤波器以及相应的乘积型指数滤波器对此接收信号的响应的归一化模。可以看到,匹配滤波器只检测到了最大的目标,而指数滤波器检测到了两个目标,对两个目标时延估计误差分别为0、0(单位同上);乘积型指数滤波器也检测到了两个目标,对两个目标时延估计误差分别为0、0。
(a)匹配滤波器
(b)指数为a=0的指数滤波器

(c)乘积型指数滤波器图5 参考信号为调频广播信号时三种滤波器输出响应的归一化模Fig.5 Normalized modules for the output response of the three filters when the reference signal is an FM broadcast signal
让输入信噪比在[-20,10] dB内变化,图6给出了三种滤波器对最大目标时延估计的均方差误差随着输入信噪比变化的曲线图,其中数值仿真平均次数为5 000次。图中,指数滤波器和乘积型指数滤波器的估计误差曲线的突然中止表示估计误差减小为0,而取对数结果为负无穷所以无法显示。从图6可以看到,当输入信噪比小于-15 dB时,具有最大输出信噪比的匹配滤波器有最低的估计误差;随着信噪比的增加,当输入信噪比大于-15 dB时,乘积型指数滤波器具有最低的估计误差。
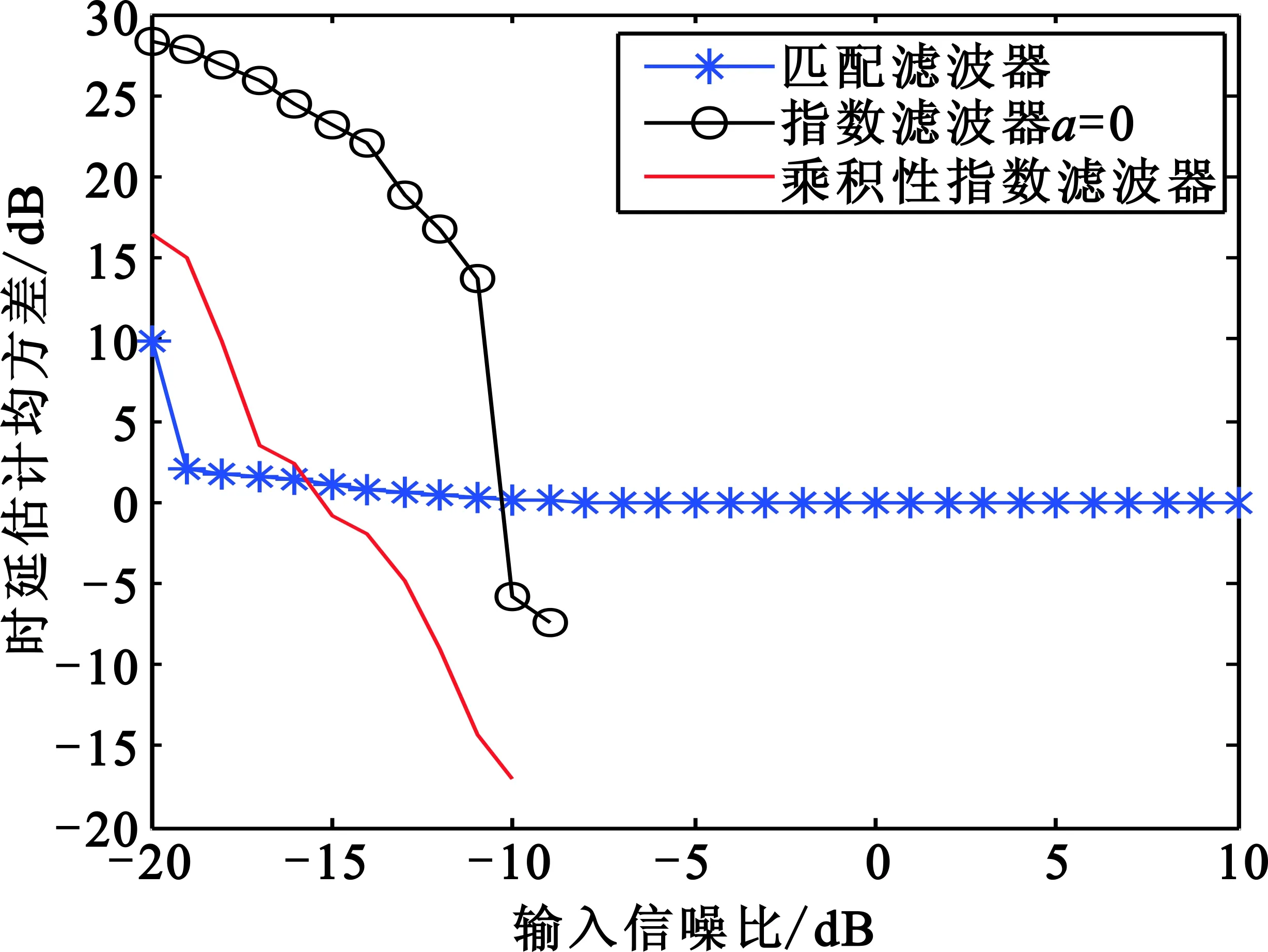
图6 参考信号为调频广播信号时三种滤波器时延估计均方差误差(指数a=0)Fig.6 Mean variance errors of delays of the three filters(a=0) when the reference signal is an FM broadcast signal
6 结束语
本文研究了多目标情况下的目标时延估计问题。指数滤波器是一类新构造的输出信噪比和目标时延分辨力随指数变化的滤波器,在损失一定输出信噪比的前提下可有效提高目标时延分辨力,从而提高目标时延估计精度,但研究表明仅采用单个指数滤波器仍存在输出信噪比和目标时延分辨力达不到实际需求的情况。
本文在乘积型高阶模糊函数乘积运算的启发下,通过乘积运算融合多个指数滤波器分别在输出信噪比和目标分辨力上的优点,构造了一个新的多目标时延估计滤波器——乘积型指数滤波器,并进一步研究了乘积型指数滤波器的输出信噪比和时延分辨力等性能。和指数滤波器不同的是,乘积型指数滤波器在保证较高单目标输出信噪比的同时也具有较单个指数滤波器更高的目标时延分辨力。特别地,如果滤波器中的一个指数滤波器取为匹配滤波器,那么该滤波器较之传统匹配滤波器具有更理想的多目标时延估计精度,并且算法易于实现,可用于实时性要求严苛的多目标参数估计任务。仿真表明,当参考信号为相位编码信号,对于中等输入信噪比,乘积型指数滤波器较之单一的指数滤波器和匹配滤波器有更低的时延估计误差;当参考信号为FM调频广播信号时,对于大于-15 dB的输入信噪比,乘积型指数滤波器具有更低的时延估计误差。为达到更高的目标时延估计精度,下一步的研究可考虑结合CLEAN技术和乘积型指数滤波器来实现多目标时延的逐次估计。
:
[1] GU Y,GOODMAN N A. Information-theoretic compressive sensing kernel optimization and Bayesian Cramér-Rao bound for time delay estimation[J].IEEE Transactions on Signal Processing,2017,65(17):4525-4537.
[2] SUN M,PINEL N,WANG Y,et al.Estimation of time delay and interface roughness by GPR using modified MUSIC[J].Signal Processing,2016,132(C):272-283.
[3] 江雪,刘源源,雷维嘉,等. 低信噪比下互相关时延估计器的FPGA实现[J].电讯技术,2014,54(7),951-957.
JIANG Xue,LIU Yuanyuan,LEI Weijia,et al.FPGA realization of cross-correlation time delay estimator under low SNR[J].Telecommunication Engineering,2014,54(7):951-957.(in Chinese)
[4] RICHARDS M .雷达信号处理基础[M].邢孟道,王彤,李真芳,等,译.2版.北京:电子工业出版社,2017.
[5] VAN H L. Detection,estimation,and modulation theory:radar-sonar signal processing and Gaussian signals in noise[M].New Jersey:John Wiley & Sons,Inc.,2002.
[6] LI X,MA X,YAN S,et al.Super-resolution time delay estimation for narrowband signal[J].IET Radar Sonar and Navigation,2012,6(8):781-787.
[7] 邱天爽,王宏禹. 一种基于最大熵谱估计的高时延分辨力时间延迟估计方法[J].电子科学学刊,1997,19(2):269-273.
QIU Tianshuang,WANG Hongyu. A high resolution time delay estimation based on the maximum entropy power spectrum estimation[J].Journal of Electronics,1997,19(2):269-273.(in Chinese)
[8] 巴斌,郑娜娥,朱世磊,等. 利用蒙特卡罗的最大似然时延估计算法[J].西安交通大学学报,2015,49(8):24-30.
BA Bin,ZHENG Na′e,ZHU Shilei,et al.A maximum likelihood time delay estimation algorithm using Monte Carlo method[J].Journal of Xi′an Jiaotong University,2015,49(8):24-30.(in Chinese)
[9] ZHANG L,DENG K,WANG H Q,et al.Exponential filter based delay estimation algorithm for active systems in the presence of multi-targets[J].IET Radar,Sonar and Navigation,2013,7(3):287-294.
[10] ZHANG L,DENG K,WANG H Q,et al.Time-delay estimation of multiple targets with wavelet based phase-only matched filter[J].International Journal of Electronics,2014,101(7):963-975.
[11] PORAT B,FRIEDLANDER B.Asymptotic statistical analysis of the high order ambiguity function for parameter estimation of polynomial-phase signals[J].IEEE Transactions on Information Theory,1996,42(3):995-1001.
[12] 李琳.低信噪比多项式相位信号的检测与参数估计[D].重庆:重庆大学,2015.
LI Lin. Detection and parameter estimation of polynomial phase signal in low SNR[D].Chongqing:Chongqing University,2015.(in Chinese)
[13] BARBAROSSA S,SCAGLIONE A,GIANNAKIS G B. Product high-order ambiguity function for multi-component polynomial-phase signal modeling[J].IEEE Transactions on Signal Processing,1998,46(3):691-708.
[14] WANG Y,ABDELKADER A C,ZHAO B,et al.Imaging of high-speed manoeuvering target via improved version of product high-order ambiguity function[J].IET Signal Processing,2016,10(4):385-394.
[15] NUNN C J,COXSON G E. Poly phase pulse compression codes with optimal peak and integrated sidelobes[J].IEEE Transactions on Aerospace and Electronic Systems,2009,45,(2):775-781.
[16] NITZBEGE R. Radar signal processing and adaptive systems[M].Boston:Artech House Press,1999.
[17] SCAGLIONE A,BARBAROSSA S. On the spectral properties of polynomial-phase signals[J].IEEE Signal Processing Letters,2016,5(9):237-240.

