一种采用刀切法的单通道信源数估计算法*
(长沙理工大学 电气与信息工程学院,长沙 410114)
1 引 言
信源数的判定是阵列信号处理领域的关键问题[1-2]。准确的信源数信息是其他阵列信号参数进行高分辨估计的前提,若信源数未知或估计不准,势必导致后续相关算法的性能大幅下降,因此准确的信源数估计具有一定的实际意义。
许多学者根据不同的准则提出了不同的估计方法,其中最常见的一种是基于信息论准则的估计算法,包括Akaike信息论(Akaike′s Information Crilertion,AIC[3])和最小长度描述准则(Mininum Description Length,MDL[4])。这些方法都是通过组合特征值分解、最大似然函数和一些罚函数来进行检测,优点是计算简单,不需认为设置门限,但当接收信号包含色噪声时易失效。文献[5]利用接收信号的延时相关信息重构协方差矩阵并结合对角加载技术对信源数进行估计,有效克服了上述缺点。另一种是通过比较盖氏圆半径大小来估计信源数,称为盖氏圆盘估计法(Gerschgorin′s Disk Estimation,GDE[6]),在色噪声环境下能有效实现信源数估计,缺点是低信噪比时检测效果较差。文献[7]直接对宽带信号阵列进行快速傅里叶变换,得到了一种在色噪声环境下估计宽带相干信源数的方法。
由于现有信源数估计算法都是针对阵列信号,不能直接用于单通道接收模型,结合间隔抽样和刀切法,提出了一种改进算法。该算法首先通过间隔抽样实现单通道接收信号空间的矢量化,接着采用刀切法对此矢量化空间重构协方差矩阵以便高效利用现有数据和抑制噪声的影响。实验结果表明,与常规算法相比,该算法在信噪比较低和采样数较少的情况下具有较好的检测性能。
2 信号模型描述
2.1 信号模型
对一个阵列接收信号,假设有p个通道同时接收信号,接收信号中包含q个源信号,那么信号接收模型可表示为[8-10]
x(t)=As(t)+n(t) 。
(1)
式中:x(t)∈p×l为观测信号,A∈p×q为混合矩阵,s(t)∈q×l为源信号,n(t)∈p×l为噪声。
由于噪声与源信号相互独立,且是均值为0的随机过程,则观测信号的协方差矩阵表示为
(2)

(3)
式中:λ1>λ2>…>λq>λq+1=…=λp是R按照降序排列出来的特征值,ui是λi对应的特征向量。
2.2 常规的信源数估计算法
常规的信源数估计算法包括基于AIC、MDL和GDE准则的信源数估计算法。AIC和MDL准则由似然函数和罚函数两部分组成:
AIC(k)=2N(M-k)lbf(k)+2k(2M-k) ,
(4)
MDL(k)=N(M-k)lbf(k)+0.5(2M-k)lbN。
(5)
GDE准则本质是通过比较特征向量来估计信源数。该方法首先对采样协方差矩阵Rj进行酉变换:
RM=THRjT。
(6)
经变换后可得
(7)
矩阵RM中半径非零的盖氏圆盘的个数即为信源数的估计值。在实际工程应用中,采用如下函数来估计信源数:
(8)
式中:D(N)为与快拍数N有关的调整因子,取值在0~1之间。分别计算GDE(k)在1≤k≤p之间的值,当GDE(k)的值首次小于零时停止计算,信源数的估计值取k-1。
在色噪声环境下,基于AIC和MDL的信源数估计算法的检测性能急剧下降,甚至失效。本文引入对角加载技术[11-12],对噪声特征值进行某种修正,即
αi=λi+λD。
(9)
式中:λi(i=1,2,…,p)为采样协方差矩阵原有的特征值,λD为加载量,αi为加载后的特征值。λD的选取是对角技术的关键。文献[13]提出了一种λD选取的经验值:
(10)
2.3 刀切法的基本原理
刀切法(Jackknife)的目的是降低估计的偏差,其基本思想是从样本集中一次删去若干个数据,对一系列剩余样本计算估计值,在估计值中得到最优估计[14]。假设样本X=(x1,x2,…,xn)独立同分布,θ=θ(x1,x2,…,xn)为未知参数θ的一个有偏估计,则θ的偏差为
(11)

(12)
θ的刀切法估计的偏差为[15]

(13)
结合式(11)和式(13)可知,估计偏差由o(n-1)变成o(n-2),复杂度降低,准确性得到提高。所以,刀切法估计可以近似为无偏估计。
3 采用刀切法的单通道信源数估计算法
在单通道接收信号时,只有一个传感器可以利用,观测数据只能获得一个,假设有两个源信号被单个传感器接收,则式(1)可表示为
x(t)=a1(t)s1(t)+a2(t)s2(t)+n(t)。
(14)
式中:a1、a2为比例因子;s1(t)、s2(t)为源信号;n(t)为噪声。
假设输入信号x(t)满足采样条件,忽略噪声的影响,对其进行周期为Δ的采样,则输入信号x(t)的离散形式为
x(kΔ)=a1s1(kΔ)+a2s2(kΔ) 。
(15)
对离散信号x(kΔ)进行周期为T的采样,令t=kT+iΔ,i=1,2,…,M则新序列x(i)(kT)为
x(i)(kT)=x(kT+iΔ) 。
(16)
式中:x(kT+iΔ)=a1s1(kT+iΔ)+a2s2(kT+iΔ),i=1,2,…,M。
由此可知,如果序列x(kΔ)按周期T进行抽样,且新序列的采样周期T是Δ的整数倍,即T/Δ=M(M∈),则通过M倍抽样,可将单通道信号分解为M通道信号,用公式表示为
(17)
将单通道接收信号升维后,可运用现有的阵列信号处理算法对信源数进行估计。为了充分利用接收到的数据,实现更加精准的估计,采用刀切法对信源数目进行估计。在刀切法中,对一个包含N个元素的集合X,X=[X(1),X(2),…,X(N)]从其中随机选取M个元素组成一个新的集合XM:
(18)
式中:XM⊂X,x(t)∈X,t=1,2,…,M且M=rN,0.5≤r<1。重复上述过程k次,得到协方差矩阵Rj:
(19)
对得到的协方差矩阵Rj进行特征值分解:
(20)
(21)
下面从理论上验证采用刀切法重构的协方差矩阵Rj能有效抑制高斯噪声的影响。
证明:当整个样本的信源数检测概率p大于50%时,pj表示采用刀切法后信源数的检测概率,则pj≥p。分两种情况验证。
当Z=2n时,即迭代次数为偶数时,采用刀切法后的检测概率pj为

(22)
式中:p为正确检测的概率,q为错误检测的概率。同理可得当Z=2n+1时,pj≥p。所以不管迭代次数Z取何值,都有pj≥p,得证。
基于以上分析可知,本文提出的算法能够适用于单通道模型,并能有效抑制高斯白噪声和高斯色噪声的影响。图1给出了本文算法流程图。

图1 本文算法的流程框图Fig.1 Flow chart of the proposed algorithm
利用刀切法提高信源数的检测概率是以增加算法复杂度为代价的。设定阵元数M=8,快拍数T=1 000,迭代次数Z=20,采样比例r=0.625。由于在多次采用刀切法和酉变换的过程中,计算相互独立,本文算法可通过并行计算方式处理,此时常规算法的运行时间是0.002 9 s,本文算法的运行时间是0.003 2 s。常规算法GDE和本文算法的算法复杂度如表1所示。

表1 常规GDE算法与本文算法的复杂度分析Tab.1 Complexity analysis of GDE algorithm and improved algorithm
从表1中可知,虽然本文算法需要多次循环迭代处理,但都可以通过增加空间负荷来减少计算时间。对比常规算法和本文算法,除在取最大频次过程中的时间复杂度有所不同外,其余基本一样。
4 实验仿真与分析
为了最大程度模拟真实情况下的信源数检测性能,分别在白噪声和色噪声环境下进行仿真分析。由于常规算法的检测性能会随着快拍数的减少而下降,因此本文取快拍数T=2 000。
实验1:假设单通道接收信号中包含3个信号源,经AD采样后取快拍数T=2 000,采用间隔抽样法构建12个虚拟通道,使得单通道接收信号转换成阵列信号的形式。设定信噪比变化范围为-15~15 dB,以2 dB递增,分别在白噪声和色噪声环境下进行200次蒙特卡洛实验,基于AIC准则和MDL准则方法、GDE方法和本文算法的检测概率如图2所示。

(a)白噪声环境下

(b)色噪声环境下图2 四种算法检测性能与信噪比的关系Fig.2 The relationship between performance and SNR of four algorithms
从图2中可以看出,当信噪比低于-7 dB时,三种常规算法的性能急剧下降,而本文算法的检测概率仍然较高。在色噪声环境下时,基于信息论的AIC准则和MDL准则对信源数失去了准确估计;当信噪比为-7 dB时,GDE方法的检测性能为0.7,而本文算法的检测概率已收敛于1。因此当通道噪声为白或色噪声时,相比其他三种常规算法,本文算法具有良好的检测性能。
王超,范雪冰,佟首峰,等.空间光到少模光纤的耦合效率及影响因素[J].光子学报,2018,47(11):1206001
实验2:假设一单通道接收信号中包含3个复指数信号,设定信噪比为-5 dB,采样快拍数T=2 000,图3表示了本文算法的检测概率与嵌入维数的关系。从图3中可以看出,本文算法的检测概率随嵌入维数的增加呈先上升后下降的趋势。当嵌入维数小于7时,检测概率低于0.5,因为间隔抽样后的协方差矩阵不能完全包括原单通道接收信号的全部信息;当嵌入维数高于12时,检测概率呈下降趋势,因为嵌入维数过多,各分量之间会相互干扰。
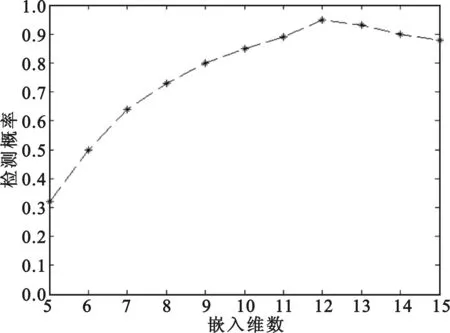
图3 嵌入维数的选择对算法性能的影响Fig.3 The influence of embedding dimension on algorithm performance
实验3:假设一单通道接收信号中包含3个复指数信号,在高斯白噪声环境下设定信噪比为10 dB,采样快拍数由100变换到1 000;在色噪声环境下设定信噪比为-7 dB时,采样快拍数由1 000以200递增到3 000,每种实验进行200次蒙特卡洛实验。图4为四种算法在不同快拍数下的正确检测概率。

(a)SNR=10 dB,白噪声环境下
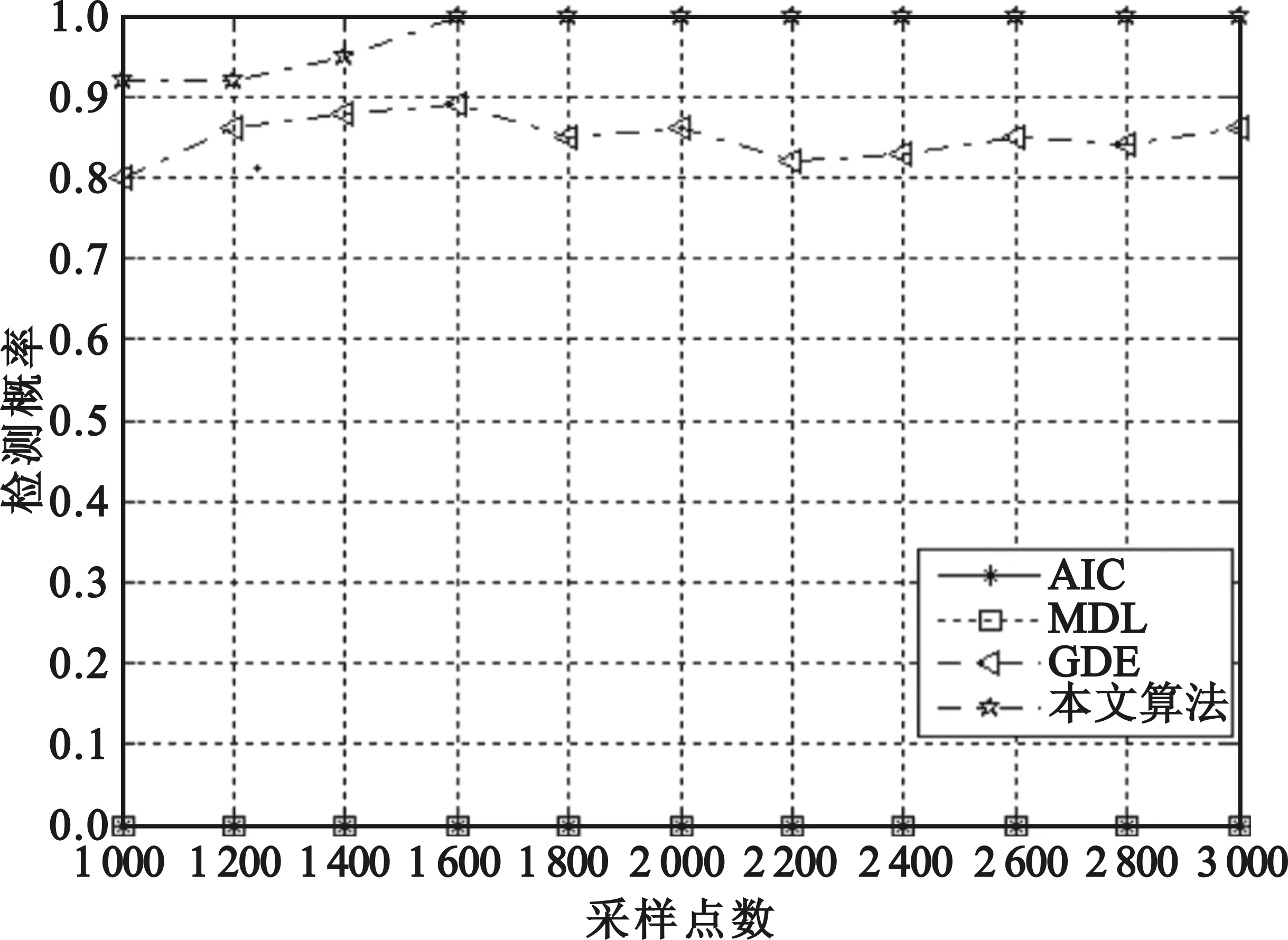
(b)SNR=-7 dB,色噪声环境下图4 四种算法估计性能与采样点数的关系Fig.4 The relationship between the estimation performance of four algorithms and the number of sampling points
由图4的仿真结果可知,当通道噪声为高斯白噪声时,四种算法的检测概率都随快拍数的增大而提高。当快拍数低于200时,AIC方法的检测性能最好,本文算法略低于AIC算法但明显高于MDL和GDE算法;当快拍数高于300时,本文算法的检测概率优先收敛1。当通道噪声为高斯色噪声时,本文算法的检测概率明显优于其他三种算法,保持了良好的检测性能。
实验4:为了获得更加精确的估计结果,选择200组实测数据分别在信号源为2个和3个的情况下采用四种算法对信源数进行估计。表2和表3的数字表示四种算法估计不同信源数的次数。

表2 2个信源的估计结果Tab.2 Estimation results of two signals

表3 3个信源的估计结果Tab.3 Estimation results of three signals
从表2和表3可知,当信源数个数为2时,AIC准则、MDL准则、GDE准则和本文算法的估计正确概率分别为81%、85%、82.5%和92.5%;当信源数个数为3时,四种算法的估计正确概率分别为65%、80%、58%和87%。由此可知,在不同信源数下,本文算法检测的正确概率优于其他三种算法。
5 结束语
本文针对现有信源数估计存在的问题,提出了一种改进算法。该算法首先采用间隔抽样法有效地解决了现有算法无法直接用于单通道信源数估计的问题,然后利用刀切法重构多个协方差矩阵,并多次进行酉变换,充分利用有限信息,避免了因舍去相关的信号分量造成误差。仿真实验表明,与原有算法相比,在低信噪比和低快拍数下,本文提出的改进算法在白噪声和色噪声环境中的检测性能得到了较大改善。本文算法的不足在于只研究了高斯噪声下的单通道信源数估计问题,因此还需要对非高斯噪声的情况进一步探索。
:
[1] PAZOS S,HURTADO M,MURAVCHIK C.On sparse methods for array signal processing in the presence of interference[J].IEEE Antennas & Wireless Propagation Letters,2015,14(5):1165-1168.
[2] LIU W.Antenna array signal processing for quaternion-valued wireless communication systems[C]//Proceedings of 2014 IEEE Benjamin Franklin Symposium on Microwave and Antenna Sub-systems for Radar,Telecommunications,and Biomedical Applications(BenMAS).Philadelphia,PA,USA:IEEE,2014:1-3.
[3] CHAKRABARTI A,GHOSH J K.AIC,BIC and recent advances in model selection[J].Philosophy of Statistics,2011(2):583-605.
[4] NANNEN V.A short introduction to model selection,kolmogorov complexity and minimum description length(MDL)[J].Computer Science,2010,46(2):446-464.
[5] 程晨,韩惠莲,司伟建.基于延时处理的对角加载信源数估计方法[J].云南大学学报(自然科学版),2014(6):823-829.
CHENG Chen,HAN Huilian,SI Weijian.The sources number estimation using delay correlation processing based on diagonal Loading[J].Journal of Yunnan University(Natural Sciences Edition),2014(6):823-829.(in Chinese)
[6] LU Z,GAO M,JIANG H.Source number estimation for minimum redundancy arrays with Gerschgorin disk estimator[C]//Proceedings of 2012 IEEE 11th International Conference on Signal Processing(ICSP).Beijing:IEEE,2012:311-314.
[7] 周围,王新青,闫霄翔,等.空间平滑和盖氏半径变换的宽带相干信源数估计[J].重庆邮电大学学报(自然科学版),2014(3):346-351.
ZHOU Wei,WANG Xinqing,YAN Xiaoxiang,et al.Estimation of wideband coherent source number based on spatial smoothing and transformed Gerschgorin radii[J].Journal of Chongqing University of Posts and Telecommunications(Natural Science Edition),2014(3):346-351.(in Chinese)
[8] CHENG W,LEE S,ZHANG Z,et al.Independent component analysis based source number estimation and its comparison for mechanical systems[J].Journal of Sound and Vibration,2012,331(23):5153-5167.
[9] SHOJAFAR M,ABOLFAZLI S,MOSTAFAEI H,et al.Improving channel assignment in multi-radiowireless mesh networks with learning automata[J].Wireless Personal Communications,2015,82(1):61-80.
[10] SHOJAFAR M,CORDESCHI N,BACCARCLLI E.Energy-efficient adaptive resource management for real-time vehicular cloud services[J].IEEE Transactions on Cloud Computing,2016,2(3):1-14.
[11] 伍警,蒋鸿宇,李兵,等.非均匀天线组阵中引入对角加载的合成算法[J].电讯技术,2017,57(6):710-715.
WU Jing,JIANG Hongyu,LI Bing,et al.A combining algorithm using diagonal loading for non-uniform antenna arraying[J].Telecommunication Engineering,2017,57(6):710-715.(in Chinese)
[12] CHENG Q,PAL P,TSUJI M,et al.An MDL algorithm for detecting more sources than sensors using outer-products of array output[J].IEEE Transactions on Signal Processing,2014,62(24):6438-6453.
[13] 谢纪岭,司锡才.基于协方差矩阵对角加载的信源数估计方法[J].系统工程与电子技术,2008,30(1):46-49.
XIE Jiling,SI Xicai.Determining the number of sources based on diagonal loading to the covariance matrix[J].Systems Engineering & Electronics,2008,30(1):46-49.(in Chinese)
[14] HAN K,NEHORAI A.Improved source number detection and direction estimation with nested arrays and ULAs using jackknifing[J].IEEE Transactions on Signal Processing,2013,61(23):6118-6128.
[15] HANSEN B E,RACINE J S.Jackknife model averaging[J].Journal of Econometrics,2012,167(1):38-46.

