调制方式的动态TOPSIS识别*
(海军航空大学 航空作战勤务学院,山东 烟台 264001)
1 引 言
通信对抗目标的特征选择和提取是通信对抗领域中一个重要的课题。准确识别出截获的通信信号调制方式,既是提取通信对抗目标特征参数,完成解调并获取通信信息的必然要求,也是后续进行针对性的电子干扰所必经途径。随着通信信号传播环境的日益复杂以及通信调制方式的多样化,传统的人工识别方式已经不适用。1969年4月,Waver等人[1]发表了第一篇研究自动调制识别的论文,从而拉开了信号自动调制方式识别研究的大幕。自动调制识别的出现克服了传统人工识别的缺点,能够实时、有效地对通信信号调制方式进行识别。目前,调制识别主要有两种方式,分别是基于似然函数的决策理论方法和基于特征参数的模式识别方法[2]。前者在假设信号满足某种分布条件的前提下,利用统计似然特征进行判决,而后者则先进行信号的特征提取,然后再利用不同的分类器进行判决。因此,对基于特征参数的模式识别方法而言,分类器的设计好坏将直接影响到识别正确率。目前分类器设计的方法主要有基于神经网络的方法[3-5]、基于支持向量机的方法[6-8]和基于判决树的方法[9-11]。其中,基于判决树的难点在于如何正确确定判决门限和判决准则,而基于神经网络和支持向量机的方法不需要人工确定判决门限和判决准则,适应性强,但是计算量相对较高。
针对上述问题,本文提出了基于动态TOPSIS(Technique for Order Preference by Similarity to Ideal Solution)的调制方式识别方法。与目前常用的分类器——判决树的识别流程不同,后者是对提取的特征参数依次进行门限比较,直至分选识别出每一种调制方式。而本文所提方法的思路是将多个特征参数看成一个整体,建立一个系统判决,利用各个特征参数直接对调制方式进行分类,能够有效地避免特征参数的门限选取准确性问题,同时也避免了特征参数多次利用的问题。
2 基于动态TOPSIS的调制识别算法
2.1 算法原理
TOPSIS法是一种多目标决策方法,其基本思路是定义决策问题的正理想解和负理想解,然后在所有的可行方案中找到一个方案。综合来看,该所选方案中,各个评价指标离正理想解最近,而离负理想解最远。一般来说,正理想解即是最理想的方案,要满足它所对应的属性是各方案中最好的;负理想解则是最坏的方案,要满足它所对应的属性是各方案中最差的。之后利用方案排队的决策方式,将实际值和理想解进行比较,离正理想解越近、离负理想解越远越好。
基于动态TOPSIS的调制方式识别方法其主要思路如下:首先,确定多个特征参数为评价指标,然后对每一种调制方式都进行正、负理想解的设定(以该调制方式下的特征参数理想值为正理想解,所有待判决的调制方式下特征参数的理想值中与正理想解差距最大的值为负理想解);其次,让待识别信号依次进入到每一个调制方式的TOPSIS模型中进行打分,得到多个得分;最后,对待判决的各调制方式的得分进行排序,得分最高的则为调制方式的判决结果。
2.2 具体步骤
设待判决的调制方式有M种,确定N个特征参数为评价指标。

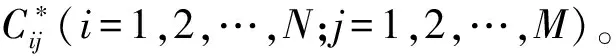
常规的TOPSIS法中,对每一个评价指标来说,其正、负理想解都是固定的,但是考虑到调制方式识别中对应一种评价指标,每一种调制方式的理想解都是不同的,因此,为了满足正理想解和负理想解的定义,将之定义为动态的理想解。
Step2 对待识别信号进行特征参数的提取,得到N个特征参数估计值hi(i=1,2,…,N)。
Step3 计算待识别信号的特征参数到各待判决调制方式的正、负理想解的距离。其中,到正理想解的距离为
(1)
到负理想解的距离为
(2)
Step4 计算待判决调制方式得分fj为
(3)
然后进行排序,得分最高的调制方式即为判决结果。
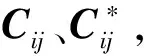

图1 调制识别流程图Fig.1 Flow chart of modulation classification
3 仿真验证
3.1 模拟调制识别
设采样后的待识别信号s(i)为
s(i)=a((i-1)ts)cos[2πfc(i-1)ts+φ((i-1)ts)],
i=1,2,…,Ns。
(4)
式中:fc为载波频率;ts=1/fs,fs为采样频率;Ns为采样点数。S(i)为s(i)的离散傅里叶变换,即
S(i)=FFT(s(i)) 。
(5)
设定待识别的模拟调制种类包括DSB、LSB、USB、AM和FM,那么可以确定幅度谱峰值γmax、谱对称性P、信号包络方差与均值平方之比R这3个特征值为评价指标[12-14]。
(1)幅度谱峰值γmax
(6)
式中:acn(i)表示零中心归一化瞬时幅度。acn(i)的计算公式如下:
(7)
(2)谱对称性P
其计算公式为
(8)
式中:PL表示s(i)的下边带功率,PU表示s(i)的上边带功率,即
(9)
(10)
(3)信号包络方差与均值平方之比R
(11)
式中:σ2表示信号包络的方差,μ2表示信号包络均值的平方。
接下来利用上述评价指标,以AM信号为例,进行基于动态TOPSIS的调制方式识别仿真分析。参数设置如下:fc=3 MHz,fs=20 MHz,Ns=10 000。

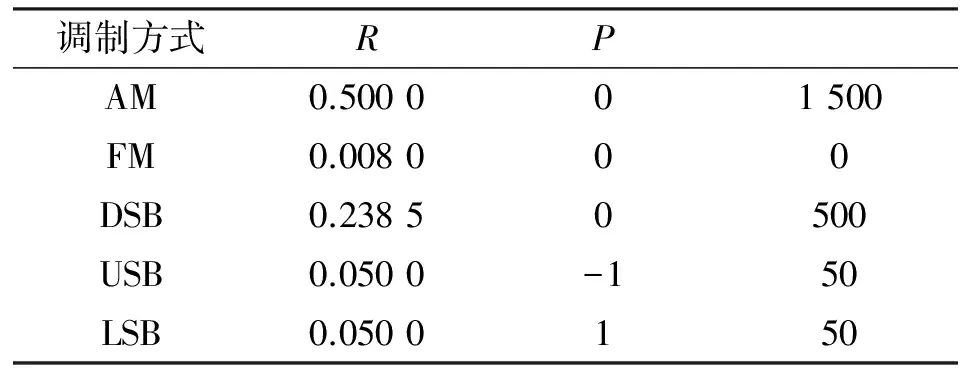
表1 模拟调制方式下正理想解Tab.1 Positive ideal solutions of analog modulation mode γmax
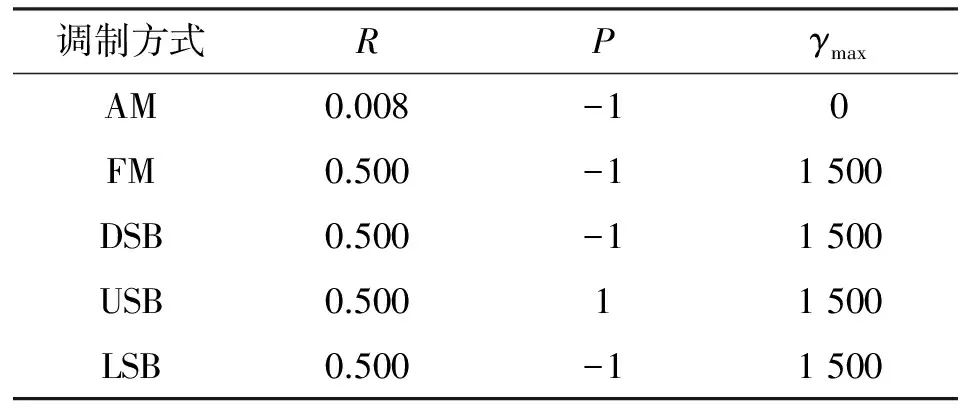
表2 模拟调制方式下负理想解Tab.2 Negative ideal solutions of analog modulation mode
接下来按照式(6)~(11)求取待识别AM信号的各特征参数,然后按照式(1)和式(2)分别计算提取的特征参数到这5种待判决调制方式的正、负理想解的距离,最后按照式(3)计算各待判决调制方式的得分。图2给出了本文方法在不同信噪比下对多种信号的正确识别率,可以看出本文方法在8 dB信噪比下就能够准确识别不同的模拟调制方式,对单边带信号甚至能够在3 dB的低信噪比下达到100%准确识别。
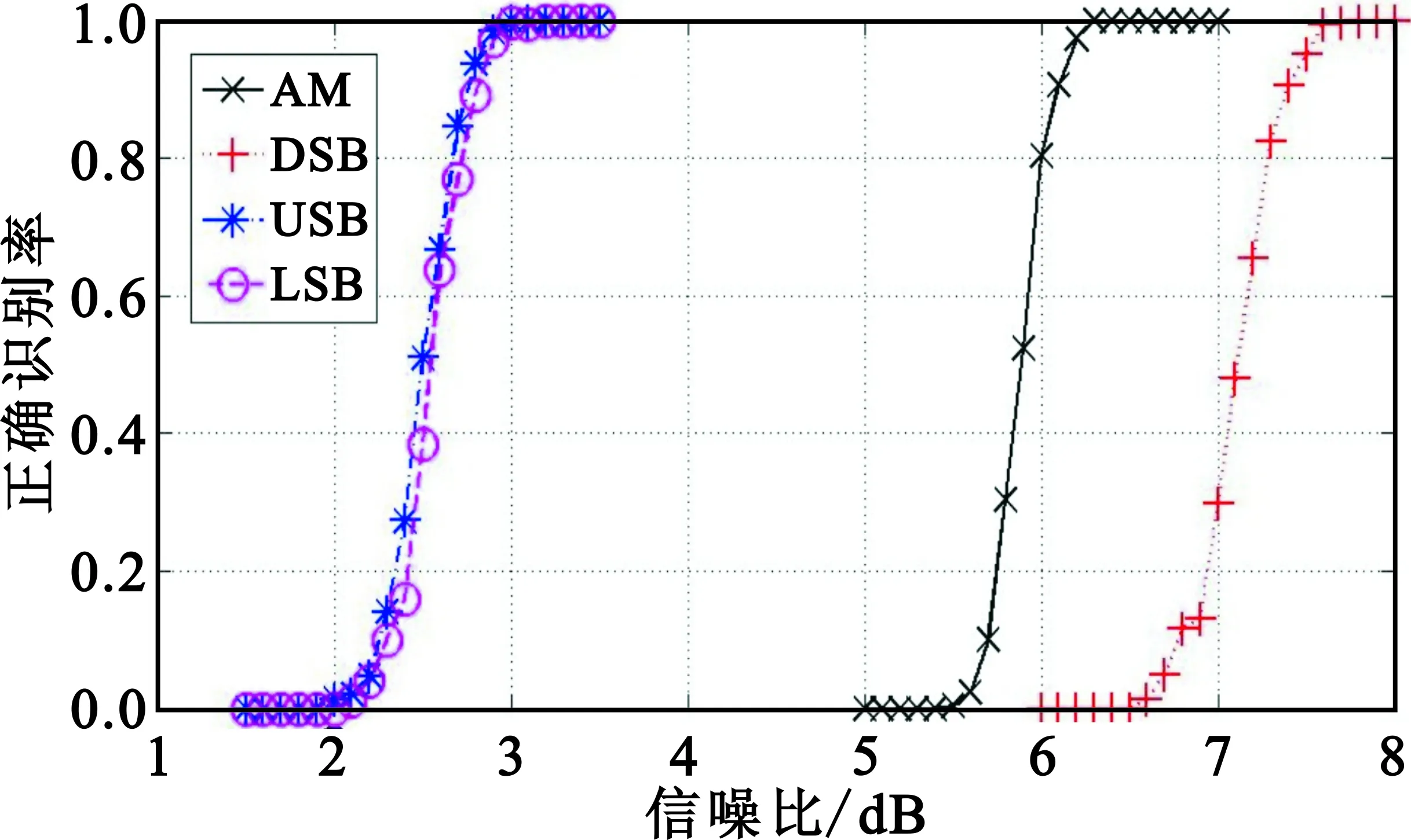
图2 调制方式正确识别率Fig.2 Correct classification rate of modulation mode
3.2 数字调制识别
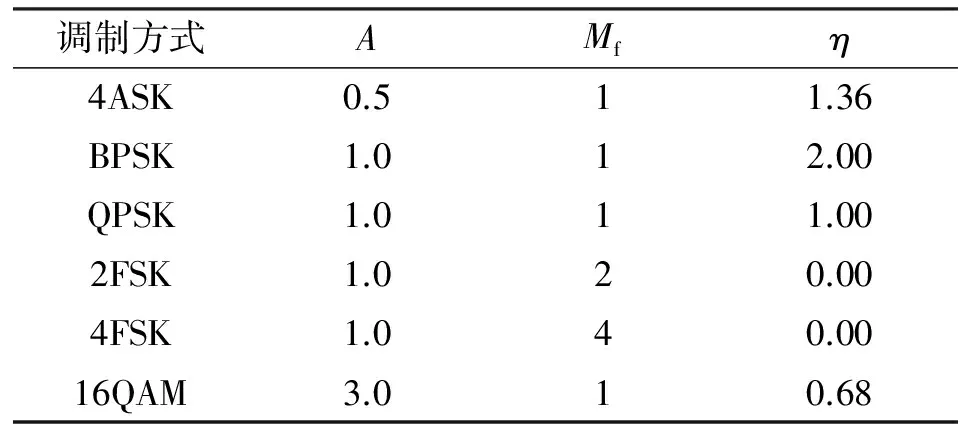
设定待识别的数字调制种类包括4ASK、BPSK、QPSK、2FSK、4FSK和16QAM,那么可以确定平均幅度A、谱峰系数Mf、高阶累积量特征值F这3个特征值为评价指标[4,13]。
(1)平均幅度A
是指所有采样点的瞬时包络的平均值,如下所示:
(12)
图3给出了不同数字调制下的平均幅度A,可以看出,ASK信号的平均幅度随着信噪比的提高而逼近于0.5,且不随进制数变化而变化;MFSK和MPSK这类恒包络信号的平均幅度则随着信噪比的提高而趋近于1,同样不随进制数变化而变化;而QAM信号的平均幅度则大于1,16QAM的平均幅度约等于3,且随着进制数的增大而增大。
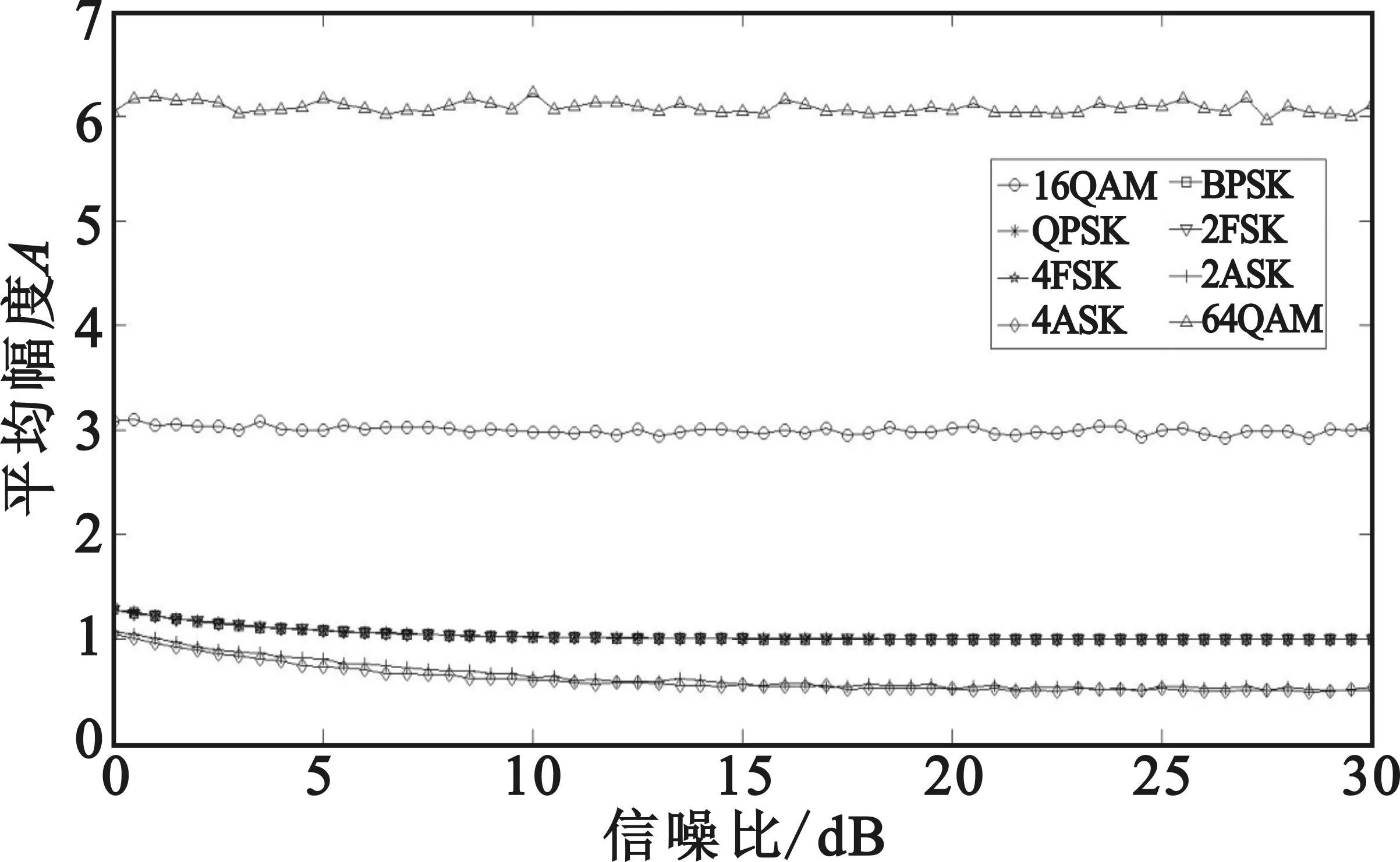
图3 不同数字调制方式的平均幅度Fig.3 Average magnitude of different digital modulation mode
(2)谱峰系数Mf
反映信号频谱峰值的多少,定义式如下:
(13)
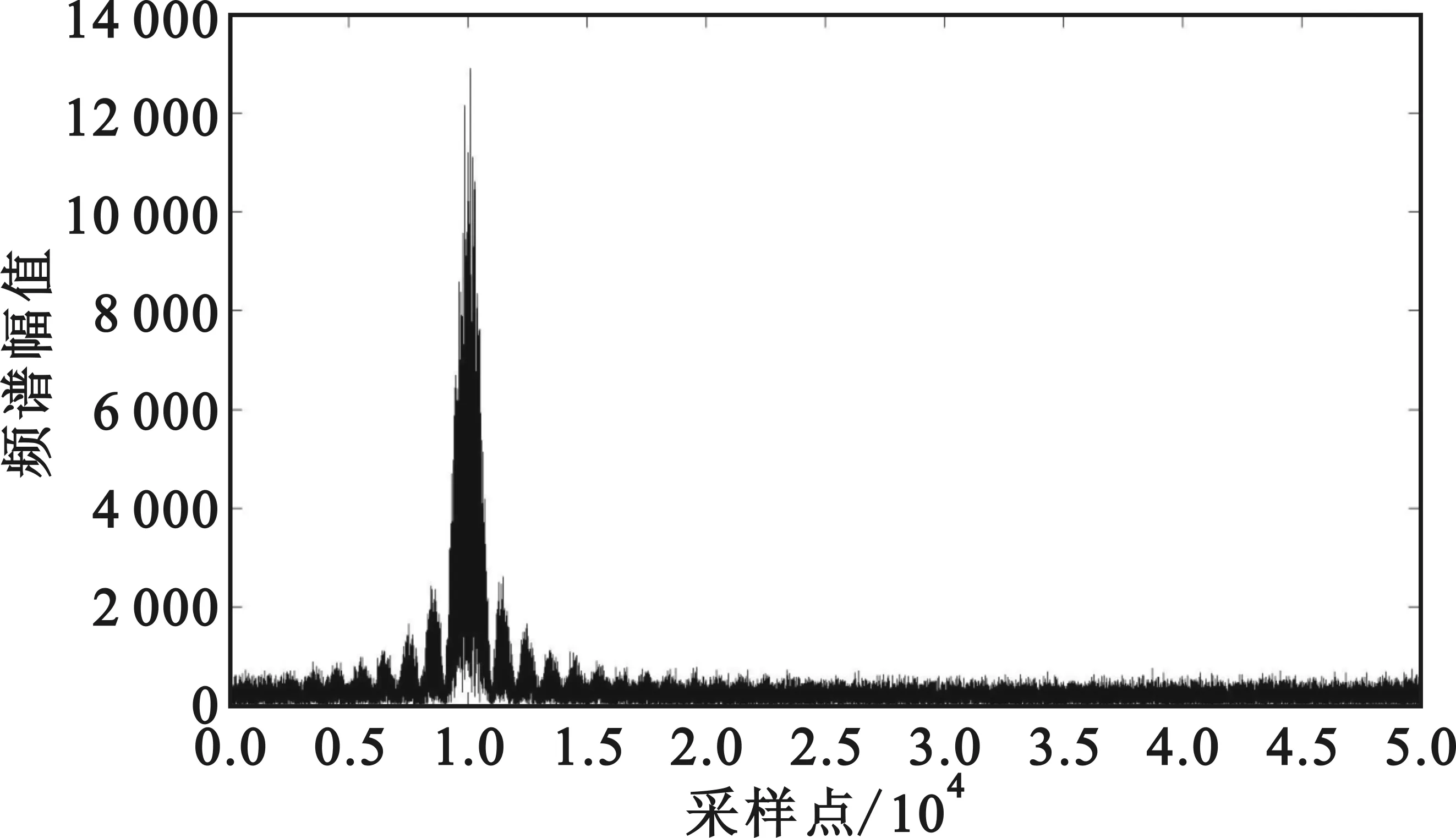
式中:Si表示信号频谱中第i个谱峰的频率值,且升值排序,即S1<…Si… (a)4FSK (b)16QAM (c)QPSK (d)4ASK图4 信噪比0 dB条件下几种数字调制信号的频谱图Fig.4 Frequency spectrogram of several digital modulation signal when SNR=0 dB (3)高阶累积量特征η 信号的高阶累积量定义为[15] ckx(τ1,…,τk-1)=cum[x(t),x(t+τ1),…,x(t+τk-1)] 。 (14) 选取二阶和四阶高阶累积量,构造特征参数η如下: η=|c40|/|c21|2。 (15) 可以推知其理论值如表3所示[4]。 表3 η理论值Tab.3 Theoretic value of η 表4 数字调制方式下正理想解Tab.4 Positive ideal solutions of digital modulation mode 表5 数字调制方式下负理想解Tab.5 Negative ideal solutions of digital modulation mode 接下来,按照图1所示的识别流程进行调制方式识别,表6和图5给出了本文方法在全频段信噪比下对多种数字调制信号的正确识别率(信号带宽约为2 kHz,噪声带宽约为250 kHz),可以看出本文方法在5 dB信噪比下能够达到90%左右的正确识别率,在10 dB时能够接近100%的正确识别。 表6 数字调制正确识别率Tab.6 Correct classification rate of digital modulation 图5 数字调制方式正确识别率Fig.5 Correct classification rate of digital modulation mode 本文借鉴TOPSIS对有限个评价对象与理想化目标的接近程度进行排序的思路,对调制信号的调制方式识别问题进行了分析,提出了可行的识别算法,并分别通过模拟调制和数字调制识别的仿真示例进行了演示。从仿真结果可以发现,本文方法能在较低信噪比条件下实现稳健的调制方式识别,且具有更强的灵活性,更低的运算复杂度。为进一步提升判决准确率,需更深入地研究特征参数选取和权值确定等问题。 : [1] BOUDREAU D,DUBUC C,PATENAUDE F.A fast automatic modulation recognition algorithm and its implementation in a spectrum monitoring application[J].IEEE Transactions on Communications,2000,48(5):732-736. [2] 吴迪,葛临东,彭华.基于EM算法的联合调制识别与参数估计[J].四川大学学报(工程科学版),2014,46(1):114-120. WU Di,GE Lindong,PENG Hua.Joint modulation classification and parameter estimation based on EM algorithm[J].Journal of Sichuan University(Engineering Science Edition),2014,46(1):114-120.(in Chinese) [3] 赵雄文,郭春霞,李景春.基于高阶累积量和循环谱的信号调制方式混合识别算法[J].电子与信息学报,2016,38(3):674-680. ZHAO Xiongwen,GUO Chunxia,LI Jingchun.Mixed recognition algorithm for signal modulation schemes by high-order cumulants and cyclic spectrum[J].Journal of Electronics & Information Technology,2016,38(3):674-680.(in Chinese) [4] 党月芳,徐启建,张杰,等.高阶累积量和分形理论在信号调制识别中的应用研究[J].信号处理,2013,29(6):761-765. DANG Yuefang,XU Qijian,ZHANG Jie,et al.Research on modulation classification based on high-order cumulants and fractal theory[J].Journal of signal Processing,2013,29(6):761-765.(in Chinese) [5] 杨发权,李赞,罗中良.基于聚类与神经网络的无线通信联合调制识别新方法[J].中山大学学报(自然科学版),2015,54(2):24-29. YANG Faquan,LI Zan,LUO Zhongliang.A new speciric combination method of wireless communication modulation recognition based on clustering and neural network[J].Journal of Zhongshan University(Natural Science edition),2015,54(2):24-29.(in Chinese) [6] 陈红,蔡晓霞,徐云,等.基于多重分形特征的通信调制方式识别研究[J].电子与信息学报,2016,38(4):863-869. CHEN Hong,CAI Xiaoxia,XU Yun,et al.Communication modulation recognition based on multi-fractal dimension characteristics[J].Journal of Electronics & Information Technology,2016,38(4):863-869.(in Chinese) [7] 李一兵,葛娟,林云.基于熵特征和支持向量机的调制识别方法[J].系统工程与电子技术,2012,34(8):1691-1695. LI Yibing,GE Juan,LIN Yun.Modulation recognition using entropy features and SVM[J].Systems Engineering and Electronics,2012,34(8):1691-1695.(in Chinese) [8] 张慧敏,柴毅.支持向量机多类分类的数字调制方式识别[J].重庆大学学报,2011,34(12):78-81. ZHANG Huimin,CHAI Yi.Digital modulation mode recognition based on multi-class classification of support vector machine[J].Journal of Chongqing University,2011,34(12):78-81.(in Chinese) [9] 马兆宇,韩福丽,谢智东,等.卫星通信信号体系调制识别技术[J].航空学报,2014,35(12):3403-3414. MA Zhaoyu,HAN Fuli,XIE Zhidong,et al.Modulation recognition technology of satellite communication signal system[J].Acta Aeronautica et Astronautica Sinica,2014,35(12):3403-3414.(in Chinese) [10] 赵知劲,胡俊伟.基于小波系数稀疏性的数字调制样式识别[J].杭州电子科技大学学报,2014,34(2):16-19. ZHAO Zhijin,HU Junwei.Digital modulation classification using sparsity of wavelet coefficient[J].Journal of Hangzhou Dianzi University,2014,34(2):16-19.(in Chinese) [11] 刘明骞,李兵兵,石亚云.Alpha 稳定分布下数字调制识别新方法[J].西安电子科技大学学报,2015,42(6):1-5. LIU Mingqian,LI Bingbing,SHI Yayun.Novel recognition method for digital modulation signals with Alpha stable noise[J].Journal of Xidian University,2015,42(6):1-5.(in Chinese) [12] 冯小平,李鹏,杨绍全.通信对抗原理[M].西安:西安电子科技大学出版社,2009:112-140. [13] 王旭.基于小波变换的通信信号特征提取与调制识别[D].贵州:贵州大学,2009:37-38. WANG Xu.Feature extraction and modulation identification for communication signals based on wavelet transform[D].Guizhou:Guizhou University,2009:37-38.(in Chinese) [14] 邓兵,张韫,李炳荣.通信对抗原理及应用[M].北京:电子工业出版社,2017:86-98. [15] 张贤达.现代信号处理[M].2版.北京:清华大学出版社,2007:263-269.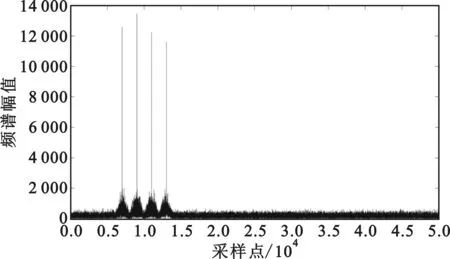
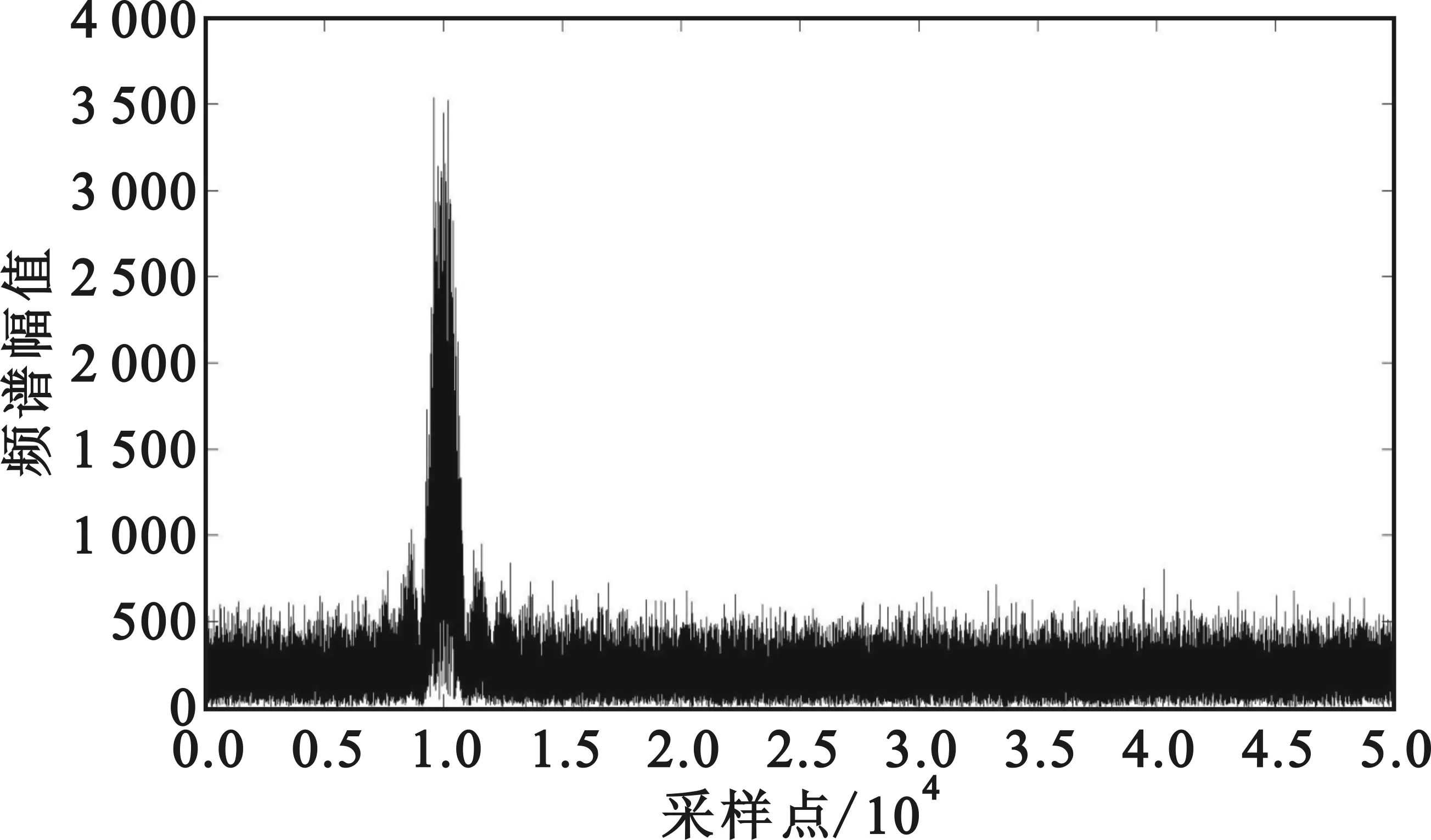
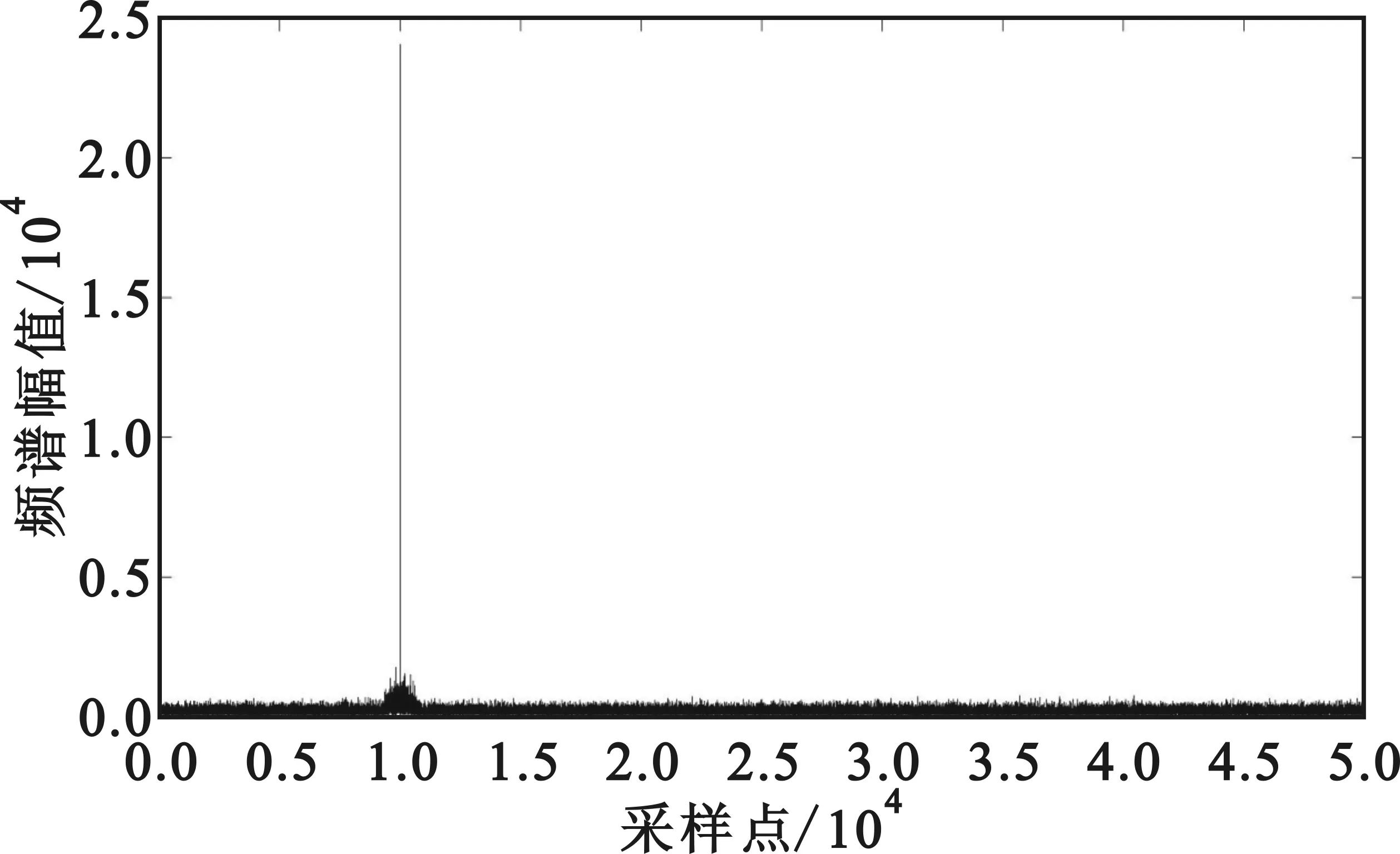

4 结 论

