电力线OFDM/OQAM通信系统信道相位预处理均衡算法*

(重庆邮电大学 通信核心芯片、协议及系统应用创新团队，重庆400065)

1 引 言

目前,各种电力线通信(Power Line Communication,PLC)协议标准中规定使用的调制技术是正交频分复用(Orthogonal Frequency Division Multiplexing,OFDM)，主要是因为这种多载波调制技术可以较好地解决多径信道所引起的频率选择性衰落，同时信道均衡也相对简单。然而，CP-OFDM技术的缺点也很明显，其中一个弊端是较差的频率选择性；另外，循环前缀(Cyclic Prefix,CP)的插入也降低了频谱效率。本文提出将5G中的一种新波形即正交频分复用/偏移正交幅度调制(Orthogonal Frequency Division Multiplexing/Offset Quadrature Amplitude Modulation，OFDM/OQAM)技术[1]引入到PLC系统中，代替了传统的CP-OFDM技术，能够获得更高的频带利用率，通过选用时频聚焦性良好的滤波器，如升余弦滤波器、扩展高斯滤波器(Extended Gaussian Function，EGF)和各向同性正交变换算法(Isotropic Orthogonal Transform Algorithm，IOTA)[2]，使其时域和频域都具有较快的带外衰减速度，能够较好地适应PLC的频率掩码[3]。

然而，OFDM/OQAM技术的引入也面临着一些难题，其中最棘手的是OFDM/OQAM系统存在着固有干扰，这种固有干扰在实数域信道下可以通过简单的迫零(Forced Zero,ZF)均衡后取实部操作来消除，但是PLC复数信道所引入的时域符号间干扰(Inter-symbol Interference,ISI)和频域载波间干扰(Inter-carrier Interference,ICI)并不能通过简单的均衡后取实部操作来消除，这将严重影响电力线通信系统的性能，因此采用行之有效的均衡算法来抑制这些干扰是很有必要的。文献[4]提出了一种两步最小均方误差(Minimum Mean Square Error,MMSE)均衡算法，首先运用MMSE均衡并通过初始判决来消除某个子载波相邻位置间的干扰，然后再用MMSE均衡来消除每个子载波上残余的符号间干扰。文献[5]提出了针对多路传输的自适应正弦/余弦调制滤波器组均衡器(Adaptive Sine/Cosine-modulated Filter Bank Equalizer for Transmultiplexer,ASCET)来实现OFDM/OQAM系统的均衡，该方法使用了3个抽头的ZF均衡器，具有比单抽头的ZF均衡更好的误码性能。文献[6]在分析了OFDM/OQAM系统固有干扰成因的基础上，提出了一种寻找常数值γ的盲均衡算法，该算法γ值的选择成为最后成功的关键，但其选择十分困难。文献[7]提出了一种迭代干扰消除均衡算法，首先通过ZF均衡对数据进行初始判决，然后依据判决值重构干扰项，最后将干扰消除。研究结果表明，上述的均衡算法能够取得比ZF均衡更好的误码性能，但是都存在复杂度过高的问题。

本文在ZF均衡的基础上提出一种基于信道相位预处理的均衡算法，性能较ZF均衡有一定提升，复杂度略高于ZF均衡，但却远低于上述其他均衡算法。该均衡算法的基本思想是在均衡前将接收信号乘上一个相位因子，尽可能使等效信道从复数域向实数域靠近，然后通过取实操作就可以消除一部分纯虚数干扰，在均衡时再除以信道函数与该相位因子乘积的实部，这样就可以有效减小掺杂在有用信号中的干扰。本文的主要贡献包括：将OFDM/OQAM技术应用到PLC系统中，并和传统的CP-OFDM技术进行了性能对比;提出了一种新颖的信道均衡方法，能获得复杂度与性能的折中，并与传统的ZF均衡进行了性能对比。

2 电力线多径信道OFDM/OQAM解调信号模型

2.1 OFDM/OQAM系统模型

OFDM/OQAM技术沿用传统的CP-OFDM技术，不同之处在于OQAM调制和滤波器的选择。图1是基于快速傅里叶逆变换(Inverse Fast Fourier Transform,IFFT)和快速傅里叶变换(Fast Fourier Transform,FFT)运算的OFDM/OQAM的系统框图。

图1 OFDM/OQAM系统结构框图Fig.1 Block diagram of OFDM/OQAM system

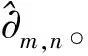
2.2 OFDM/OQAM发送信号及应用在PLC系统中满足的条件

OFDM/OQAM发送信号[8]可以表示为

(1)

式中：N表示子载波个数；am,n表示第n个符号、第m个子载波传输的符号数据，它来自于QAM映射后符号的实部和虚部；υ0表示子载波间隔；τ0表示符号实部和虚部之间的偏移间隔，τ0=T/2，且满足τ0υ0=1/2；gm,n(t)表示时频格点坐标为(m,n)的基函数。与传统CP-OFDM系统在复数域不同的是，OFDM/OQAM系统仅仅满足在实数域严格正交，实数域正交性可表示如下：

R{j(m+n-m0-n0)+(m-m0)(n+n0)·

Ag((n0-n)τ0,(m-m0)υ0)}=

δm,m0δn,n0。

(2)

式中：当m=m0时，δm,m0=1；否则δm,m0=0。实数域正交性条件可进一步解释为当m=m0，n=n0时，〈gm,n,gm0,n0〉为实数符号；不满足这一条件时，〈gm,n,gm0,n0〉为纯虚数符号。Ag(τ,υ)为模糊函数，表示为

(3)

然而，PLC是基带传输系统，若要将OFDM/OQAM应用在PLC系统中，发送信号必须为实数，文献[9]提出了OFDM/OQAM的共轭对称(Hermitian Symmetry,HS)形式，即HS-OQAM，并论证了电力线系统中实现HS-OQAM的条件为

a0,n=aM,n=0，

(4)

am,n=aN-m,n(-1)D-M-ne-jφ0。

(5)

式中：M代表离散时间偏移，M=N/2；D=L-1，L为原型滤波器长度；φ0为附加相位值，通常为了方便，取值为0。

2.3 OFDM/OQAM解调信号

PLC信道通常是多径衰落信道，典型的有4径和15径，根据著名的Zimmermann信道模型[10]可建模如下：

(6)

式中：gi为第i条路径的加权系数，表示沿着这个路径的反射和传输因子，一条路径上的反射越多，加权因子gi就越小；参数a0、a1和k都是由测量得到；τi表示第i条路径的延时。该模型代表了N条不同路径信号的叠加。

经过PLC多径信道加噪声之后，OFDM/OQAM接收信号可表示为

r(t)=h(t)⊗s(t)+η(t)=

6 Effect of continuous quality improvement on renal function in patients with chronic kidney disease of stage 3-4

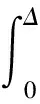
(7)

式中：h(t,τ)表示多径信道冲激响应，Δ为信道的最大时延扩展。为了便于分析，此处暂不考虑噪声的影响，则式(7)可进一步化简为

g(t-τ-nτ0)e-j2πmυ0τdτ。

(8)

假设多径信道的时延扩展Δ远小于一个符号周期,则在0≤τ≤Δ时间内，可近似认为g(t-τ-nτ0)≈g(t-nτ0)，这样式(8)可简化为

(9)

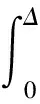
(10)

接收信号在经过了接收滤波器之后，时频格点(n0,m0)上的解调信号可表示为

(11)

3 传统ZF均衡算法

假设接收端已获得理想的信道频域响应矩阵，接收信号在经过ZF均衡后，可得到

(12)

上式等号右边第二项为待解调数据受到的周围符号的干扰。对上式进行取实部操作，结果为

(13)

上文已分析过滤波器基函数的特性，当m≠m0，n≠n0时，〈gm,n(t),gm0,n0(t)〉为纯虚数，进一步分析可发现：

(1)若为实数域信道，则干扰项为纯虚数，通过取实部操作可完全消除周围数据的干扰，恢复出原发送信号，即

(14)

(2)若为复数域信道，则干扰项为复数，通过取实部操作也不能消除周围数据的干扰，不可准确恢复出原发送信号，即

(15)

电力线OFDM/OQAM通信系统中不同子载波的频率响应各不相同且都为复数，故仅仅通过ZF均衡并不能消除周围数据符号的干扰。

4 基于信道相位预处理的均衡算法

前面已分析过在频域实数信道下，OFDM/OQAM系统能够通过取实部操作消除干扰，但是在频域复数信道下并不能。由此带来的启示是:只要在系统接收滤波和信道均衡之前采取一定的方法对接收信号进行处理，使接收信号等效信道尽量逼近实数，即让等效信道的虚部尽量小，就能够通过取实部操作消除掉大部分干扰。通常在计算干扰分量时只考虑待解调数据周围一阶邻域格点上的干扰，如图2所示。

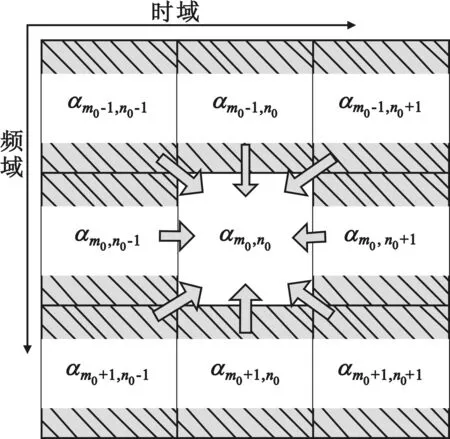
图2 一阶邻域格点干扰分布图Fig.2 The disturbance distribution of first order neighborhood lattice sites

这是因为OFDM/OQAM系统选用的滤波器一般都具有良好的时频聚焦性，距离较远的符号造成的干扰已经非常小了，可忽略不计。此时，式(11)可改写为

(16)

为描述方便，这里将复数信道频率响应表示为幅度与相位的形式：Hm=|Hm|ejφm，φm表示复数信道的相位。

对任意的子载波而言，在接收信号上乘以一个适当的相位调整因子后再进行接收滤波，此时信号变为

rm0,n0e-jφ=〈r(t)e-jφ,gm0,n0(t)〉=

am0,n0Hm0e-jφ+

(17)

分析式(17)可以发现，应尽可能选择相位调整因子e-jφ，使得频点为m0-1、m0和m0+1的等效信道为实数。实际上不可能使上述3个频点的等效信道同时为实数，但可以使某一频点的等效信道为实数，例如选择相邻前一子载波的相位作为相位调整因子e-jφm0-1，则频点为m0-1的等效信道就为实数。将e-jφm0-1代入式(17)，有

rm0,n0e-jφm0-1=am0,n0Hm0e-jφm0-1+

am0,n0Hm0e-jφm0-1+

(18)

此时再进行取实部操作，可得

R{rm0,n0e-jφm0-1}=am0,n0R{Hm0e-jφm0-1}+

(19)

式(19)等号右边第一项为有用信号，第二项为等效干扰。观察发现接收信号乘以相位调整因子e-jφm0-1并取实部之后，等效干扰分量中来自第m0-1个子载波的ICI就被消除了，此时等效干扰分量中仅剩下ISI和来自第m0+1个子载波的ICI，如图3所示。

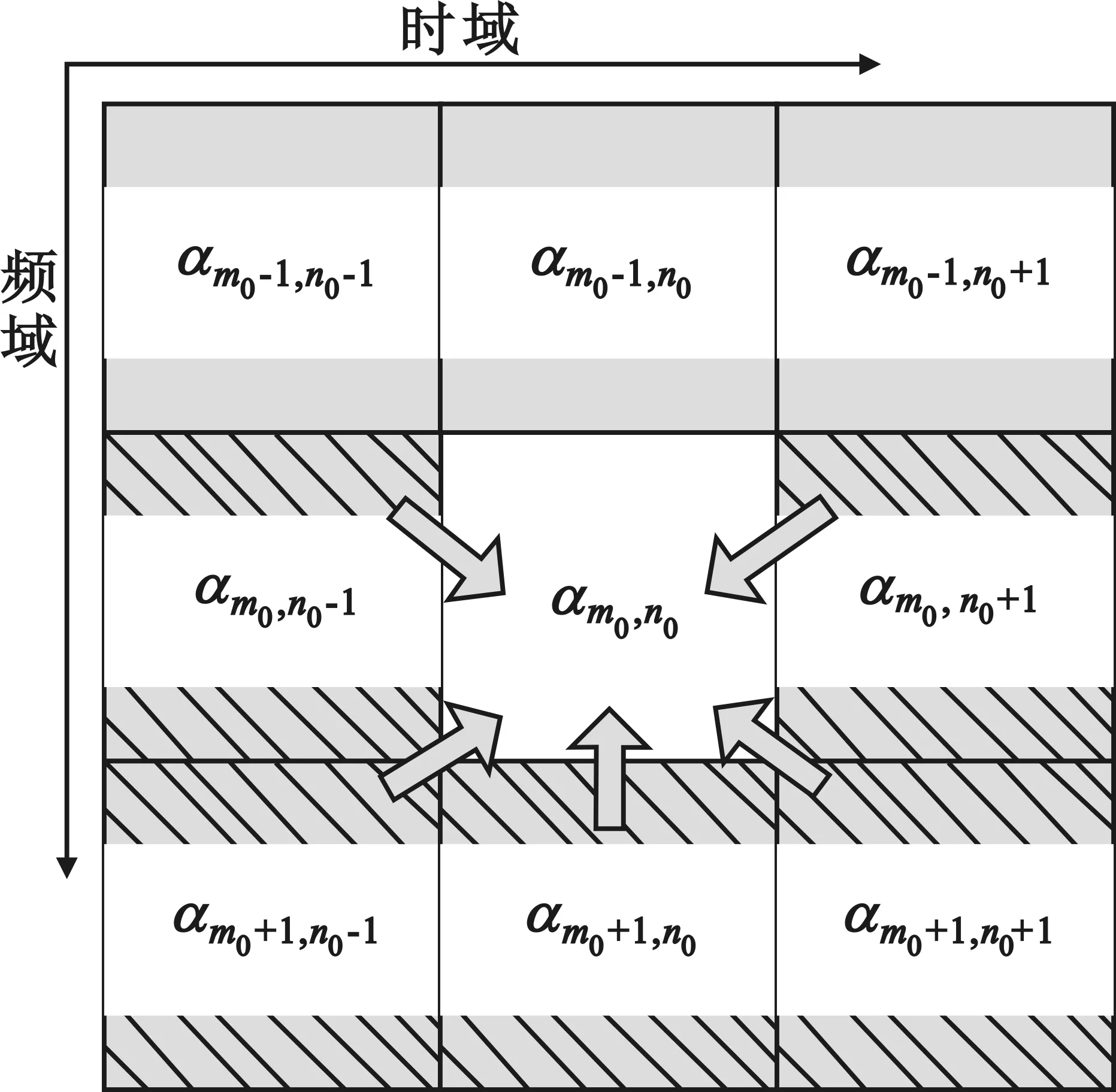
图3 相位预处理后一阶邻域格点干扰分布图Fig.3 The disturbance distribution of first order neighborhood lattice after phase pretreatment

在进行信道相位预处理之后，再采用ZF均衡，此时应除以信道频率响应与相位调整因子乘积的实部，即

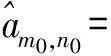
am0,n0+

(20)

对比式(12)和式(20)可以看出，信道相位预处理操作减小了解调数据符号周围的干扰分量，而计算量方面，仅仅是在接收信号的基础上乘以一个相位调整因子，若仅统计一个符号上所有子载波信道均衡的复杂度，则相比于ZF均衡，增加的复杂度主要包括计算式(18)的8N次复数乘法和计算式(20)中均衡系数时的N次复数乘法，但是由于最后在均衡时去除了第m0-1个子载波上的干扰，此时其实又减少了3N次复数乘法运算，所以信道相位预处理均衡算法相较于ZF均衡算法，总共增加了8N+N-3N=5N次复数乘法运算。由于并没有出现指数级或幂次级运算，因此所提算法增加的复杂度相对于性能的提升还是可以接受的。基于信道相位预处理的均衡算法原理框图如图4所示。

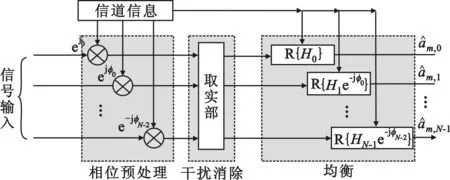
图4 基于信道相位预处理的均衡算法原理框图Fig.4 Principle block diagram of equalization algorithm based on channel phase preprocessing

5 性能仿真

5.1 参数设置

本文利用Matlab工具来进行仿真验证，在对比了OFDM/OQAM技术和传统的CP-OFDM技术应用在PLC系统中的性能之后，接着验证了所提的基于信道相位预处理均衡算法抵抗干扰的有效性，并与传统的ZF均衡进行了性能对比。仿真是以国家电网公司发布的《电力线通信解决方案-低压电力线宽带载波通信技术规范第4-1部分：物理层通信协议(报批稿)》[11]为依据，并在文献[12]中Zimmermann提出的15径慢时变信道下进行的。仿真帧数为1 000帧，其他参数如表1所示。

表1 仿真参数Tab.1 Simulation parameter

5.2 仿真结果及分析

图5所示的是PLC系统中OFDM/OQAM技术和CP-OFDM技术的性能对比曲线，两种技术是在同等的仿真条件下进行，采用的都是ZF均衡。观察图5可以发现，OFDM/OQAM系统的性能始终要好于CP-OFDM系统，这是因为OFDM/OQAM系统选用了时频聚焦性良好的IOTA滤波器，使得系统有较强的抗ICI和ISI的能力，而CP-OFDM系统尽管有循环前缀的保护，但是PLC时域信道很长的拖尾仍然会导致ISI的存在。以误码率1.0×10-6为例，OFDM/OQAM系统与CP-OFDM系统相比，大约有1 dB的性能提升。

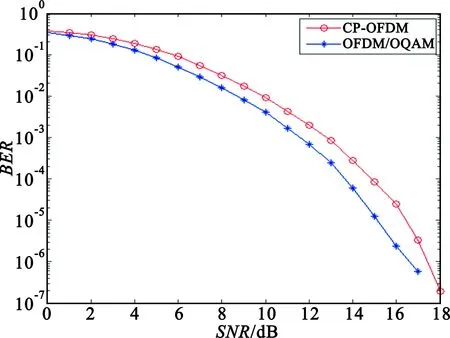
图5 OFDM/OQAM和CP-OFDM性能对比曲线图Fig.5 Performance comparison between OFDM/OQAM and CP-OFDM

图6所示的是本文提出的基于信道相位预处理的均衡算法与传统的ZF均衡算法性能对比曲线图，从图中可以看出，信道相位预处理的均衡算法性能要稍好于ZF均衡，这是因为所提均衡算法相比于ZF均衡算法，将前一子载波对当前子载波产生的载波间干扰进行了消除，还有不同符号同一频点上的子载波对当前子载波产生的符号间干扰以及后一子载波对当前子载波产生的载波间干扰都没有进行处理，所以性能没有提升太多。同样以误码率1.0×10-6为例，基于信道相位预处理的均衡算法与ZF均衡算法相比，大约有0.5 dB的性能提升。

图6 所提均衡算法与传统ZF均衡算法性能对比曲线图Fig.6 Performance comparison between proposed equalization algorithm and traditional ZF equalization algorithm

6 结束语

本文将OFDM/OQAM技术成功应用到PLC系统中，取得了比传统CP-OFDM技术更好的性能优势。但是OFDM/OQAM技术引入的滤波器仅在实数域正交，经过PLC复数域信道会产生严重的自干扰。本文在详细分析了OFDM/OQAM技术采用ZF均衡会存在残余干扰的原理后，提出了一种基于信道相位预处理的均衡算法。通过PLC15径信道的仿真，验证了所提算法比传统均衡算法具有更好的误比特率性能。需要指出，本文所提算法只消除了部分子载波的干扰，未来的研究工作可围绕进一步消除剩余子载波的干扰来展开。

：

[1] ACHAICHIA P,BOT M L,SIOHAN P.OFDM/OQAM:a solution to efficiently increase the capacity of future PLC networks[J].IEEE Transactions on Power Delivery,2011,26(4):2443-2455.

[2] RAZAVI R,XIAO P,TAFAZOLLI R.Information theoretic analysis of OFDM/OQAM with utilized intrinsic interference[J].IEEE Signal Processing Letters,2014,22(5):618-622.

[3] ALESSANDRO D S,TONELLO A M,LAMPE L.Adaptive pulse-shaped OFDM with application to in-home power line communications[J].Telecommunication Systems,2012,51(1):3-13.

[4] IKHLEF A,LOUVEAUX J.An enhanced MMSE per subchannel equalizer for highly frequency selective channels for FBMC/OQAM systems[C]//Proceedings of 2009 Workshop on Signal Processing Advances in Wireless Communications.Perugia,Italy:IEEE,2009:186-190.

[5] LIN H,SIOHAN P,TELECOM F.HS-OQAM PLC:long filter or equalizer?[C]//Proceedings of the Third Workshop on Power Line Communications(WSPLC).Udine, Italy:IEEE,2009:1-4.

[6] SAVAUX V,BADER F,NAOUES M.Blind equalization using constant modulus algorithm adapted to OFDM/OQAM modulation[C]//Proceedings of 2016 International Symposium on Wireless Communication Systems.Poznan,Poland:IEEE,2016:28-33.

[7] 孙希东.OFDM/OQAM系统在瑞利信道下的信道估计与均衡方法[J].自动化技术与应用,2016,35(3):36-41.

SUN Xidong.Channel estimation and equalization method for OFDM/OQAM systems over Rayleigh channels[J].Automation Technology and Applications,2016,35(3):36-41.(in Chinese)

[8] LIN B,TANG X,FANG X,et al.Efficient frequency-domain channel equalisation methods for OFDM/OQAM-PON with intensity modulation and direct detection[J].IET Communications,2017,11(6):872-877.

[9] LIN H,SIOHAN P.Capacity analysis for indoor PLC using different multi-carrier modulation schemes[J].IEEE Transactions on Power Delivery,2010,25(1):113-124.

[10] ABENOV R,POKAMESTOV D,GELTSER A.Multipath powerline communications channel(PLC) modelling[C]//Proceedings of 2015 IEEE International Conference on Microwaves,Communications,Antennas and Electronic Systems.Tel Aviv,Israel:IEEE,2015:1-4.

[11] 国家电网公司.Q/GDW 374.3-2016低压电力线宽带载波通信技术规范 第4-1部分：物理层通信协议(报批稿)[S].北京：国家电网公司，2016.

[12] ZIMMERMANN M,DOSTERT K.A multipath model for the powerline channel[J].IEEE Transactions on Communications,2002,50(4):553-559.