导航卫星阵列天线的快速现场系统校准算法*

(中国西南电子技术研究所，成都610036)

卫星导航(简称卫导)系统是基于无线电测距的系统，天线是实现无线电信号接收的关键部分，通过接收机对不同方向入射的卫星信号进行测量，得到不同卫星到达接收天线处的距离，从而实现几何交会定位[1]。在实际中，传统的测量型卫导天线具有稳定的相位中心，满足几何交会定位的依据；卫星信号从空间到达地面，经过路径衰减后功率位于热噪声以下，由于扩频增益，仍然能够准确地定位。全球卫星导航系统在没有干扰的环境下工作良好，但是它仍然极易受到干扰，因此在干扰环境下，研究人员引入了利用空域分集的阵列信号处理技术[2-3]。阵列天线通过多天线接收，调节不同阵元信号的幅度和相位进行合成，综合出期望的天线方向图形状，实现期望信号的接收和干扰信号的抑制[4]。现有的卫导阵列处理技术利用了卫导信号的负信噪比特性，通过功率约束实现了干扰信号的自适应调零，保证了在强干扰环境下的卫导信号可用性，但是在基于载波相位测量的高精度相对定位中，多天线的各向差异和多射频前端通道之间的不一致性将导致卫导距离测量中产生偏差，违反了几何交会定位的前提，简而言之，经过阵列处理后不具有稳定的相位中心[5]。

为了减小阵列信号处理对卫导信号中测距信息的破坏，需要对阵列天线和射频前端通道进行校准。文献[6]总结了阵列处理对卫导信号的载波相位和伪码相位产生影响的模型，比较了传统的功率倒置(Power Inversion,PI)和最小方差无失真约束(Minimum Variance Distortionless Response,MVDR)波束形成器产生的影响，但要对偏差进行约束，需要知道准确的阵列流形矢量。文献[7]提出了一种基于相关函数的阵列校准算法，实现天线阵列的空时阵列流形矢量的测量，但是没有更多地讨论校准波束的规划。文献[8]通过设置辅助跟踪通道，但只测量了阵列天线之间的相对相位，而忽略了相对幅度。文献[5]总结了卫导阵列信号处理最新的进展，指出目前卫导阵列信号处理的三大目标是可用性、准确性和完好性，而目前的功率倒置类算法只解决了强干扰环境下的可用性问题。关于目前卫导阵列抗干扰处理的现状和面临的挑战，可以参考文献[5]。

在卫导阵列信号处理需要突破的三大目标中，阵列的现场阵列流形矢量都起到关键作用[9]。为此，本文提出一种卫导阵列天线的快速现场系统校准算法。文献[10-11]讨论了在相控阵雷达中，通过设置辅助信号源的阵列误差校正。与现有文献相比，本文提出的射频通道和天线分离的系统校准方法，在对天线进行校准时，根据几何或者暗室测量的阵列流形矢量来规划校准波束，不依赖单独设置的辅助信号源，实现了卫星信号现场阵列流形矢量的快速校准。仿真验证了系统校准算法的有效性。

2 数据模型

含有卫导阵列天线的典型阵列接收系统如图 1所示。卫导信号经阵列天线接收，进入多通道射频前端进行信号调理，在数字模块中进行模拟数字转换器(ADC)采样、数字波束形成，再进入多通道数字接收机进行解调和测量，最后输出供导航定位算法使用的伪距、载波相位和多普勒等原始距离测量值。为了校准天线和射频前端对卫导信号的影响，首先建立该处理过程的数据模型。

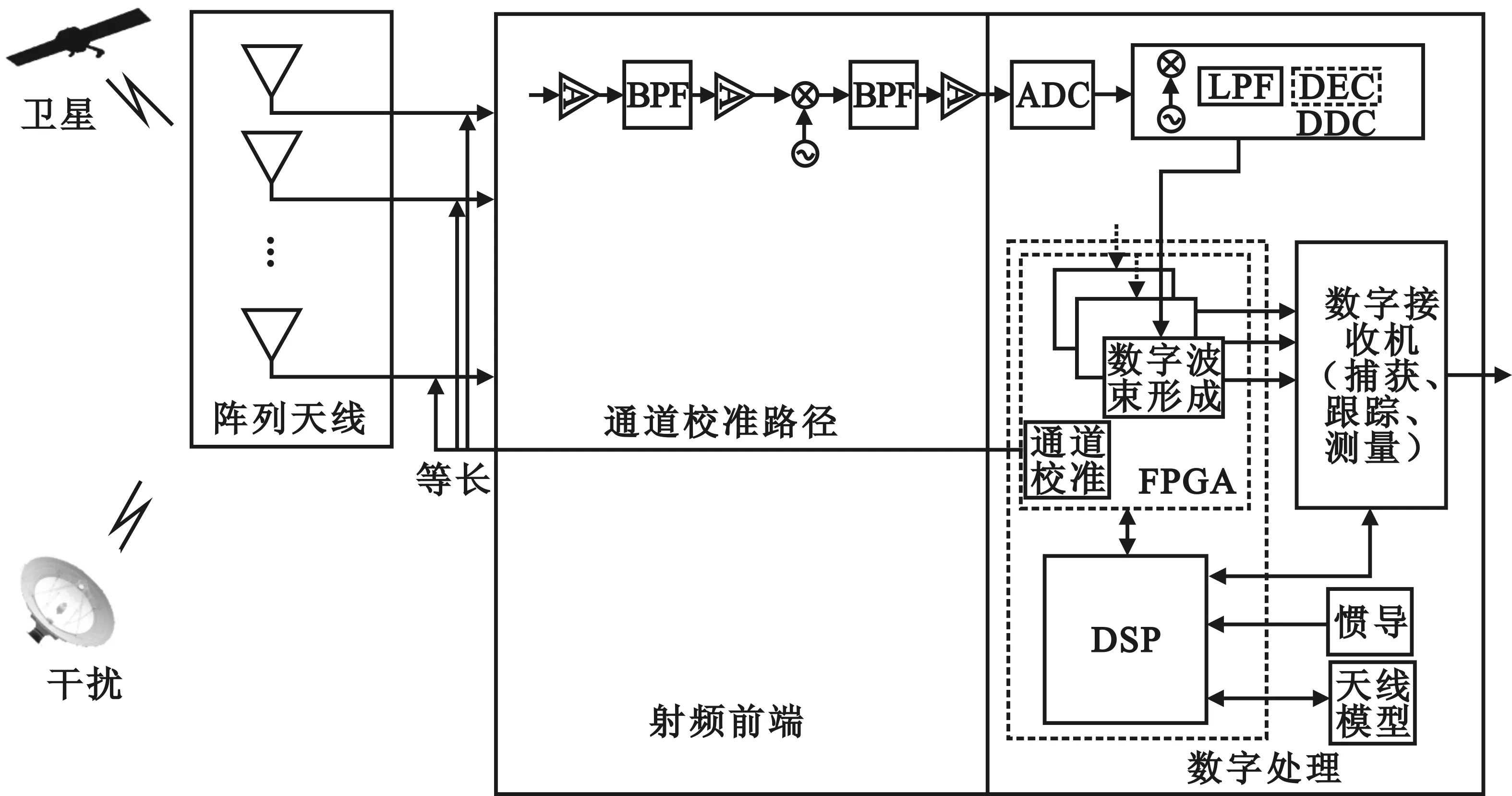
图1 卫导阵列抗干扰系统Fig.1 GNSS array anti-jamming receiver

假设第k颗卫星信号从(θ,φ)方向入射，到达第i个阵元，其复解析信号可以表示为

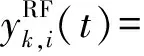
exp(j((fRF+fk,D)(t-Δtk)+ξi(θ,φ)))。

(1)

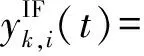
exp(j((fIF+fk,D)(t-Δtk)+ξi(θ,φ)))×

Ciexp(jψi)。

(2)

式中：Ci、ψi分别为通道引入的幅度和相位响应。值得指出的是，通道响应与信号入射方向无关。

将t时刻所有I个阵元的接收信号组成一个矢量，可以得到单颗卫星的阵列接收模型(为了简便，省略了中频上标)：

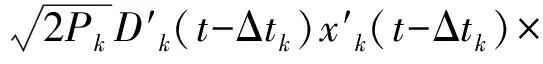
exp(j((fIF+fk,D)(t-Δtk)))。

(3)

所有K颗卫星信号同时接收，可以得到完整的阵列接收信号模型：

(4)

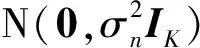
在卫导阵列信号数字波束形成中，因为卫导信号具有负信噪比，常通过功率约束，实现强干扰信号的自适应调零[2]：

minwwHRws.t.wHc=c。

(5)

zk(t)=wHyk(t)=wHa(θk,φk)sk(t)。

(6)

由wHa(θk,φk)产生的相位与信号sk(t)中由卫星到接收天线之间距离引起的相位无法区分，因此没有经过系统校准的阵列流形矢量a(θk,φk)和无约束的波束形成器w将导致卫导接收机得到的载波相位测量值无法用于基于载波相位差分的高精度相对定位应用中。为了保证经过阵列处理后卫导信号中载波相位的可用性，本文提出阵列天线的快速现场系统校准算法，旨在获得系统使用环境下的准确阵列流形矢量a(θk,φk)。

3 校准算法

根据上一节的分析，阵列流形矢量中需要进行校准的非理想差异，主要包括射频通道的不一致性和天线对不同方向入射信号的空域响应差异。前者是由射频通道之间的硬件不一致和硬件随温度等环境的不一致变化引起，通过单独的通道校准过程进行校准；后者是由于信号入射方向、天线的结构和周围环境等因素导致的阵列的接收阵列流形矢量与信号到达波程差不同产生的几何阵列流形矢量之间存在差异，通过卫星信号和数字接收机的辅助，对阵列天线的现场阵列流形矢量进行测量。

3.1 通道校准

设备自主产生校准所用的单音信号，经过数字模拟转换器(DAC)变换为模拟信号，再通过1-I功分器送往不同的射频通道入口。校准时，通过射频开关选通校准信号，经过模拟数字转换器(ADC)变换成数字信号，计算不同通道相对于参考通道之间的相关系数，获得不同通道之间的幅相不一致性。

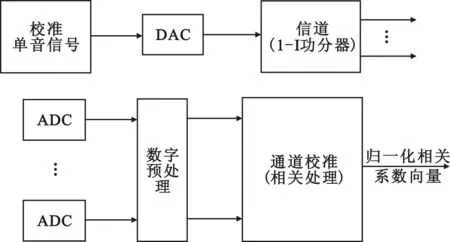
图2 通道校准处理流程Fig.2 Channel calibration procedure

记归一化的相关系数向量为h∈I×1，其各个元素计算方法如下：

(7)

式中：yi为第i个通道的接收信号，yref(t)表示参考通道接收信号，上标*表示复数共轭，t0表示通道校准的起始时刻，T表示通道校准的持续时间。通道校准就是获得归一化的相关系数向量的过程。一般在每次开机时运行，当设备需要长时间连续运行时，可在无任务阶段周期地进行通道校准。

3.2 天线校准

从式(6)中可以看出，当控制波束形成器w的幅度和相位时，实际上改变了卫导接收机的测量输入，即等价地影响了卫导信号的增益和相位。如果同时设置一系列的已知波束wm,m=1,2,…,M，对同一颗卫星信号进行跟踪，那么

(8)

式中：zk,m为第m个校准波束产生的输出信号。校准波束wm是自主设定的，zk,m(t)可以通过接收机进行测量，那么未知的现场阵列流形矢量a(θk,φk)可以通过上述观测方程直接求解：

(9)

式中：†表示矩阵的Moore-Penrose伪逆，α是一个与t时刻信号有关的归一化标量系数。通过对式(9)中所得估计向量进行归一化，可以得到与测量时间无关的第k颗卫星入射方向的归一化现场阵列流形矢量，这就是借助现场卫星信号和数字接收机的现场阵列流形矢量快速校准的基本原理。

从改善式(9)的数值计算条件，提高数字接收机的跟踪测量能力出发，对快速校准处理的流程进行设计。

Step1 根据当前第k颗卫星在天线坐标系下的入射角θi和φi，计算卫星入射方向的几何阵列流形矢量ageo(θk,φk)：

(10)

式中：pi为第i个阵元在天线坐标系下的位置矢量，作为替代也可以使用暗室测量的阵列流形矢量aac(θk,φk)，用于后续校准过程，统一记为ac0(θk,φk)。

Step2 规划校准波束的权矢量：

wk,m=ac0(θk,φk)*ejrmΔ。

(11)

式中：*表示对应元素相乘的Hadamard乘积；rm为第m个校准波束对应的随机扰动矢量，每个元素从集合{-1,0,1}中取值；Δ控制相位扰动的大小。

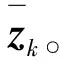
Step4 求解最小二乘问题，计算该方向现场阵列流形矢量：

(12)

根据式(4)，可将当前通道响应从现场阵列流形矢量中分离，得到净现场天线阵列流形矢量acal2(θk,φk)：

(13)

式中：hi,i=1,2,…,I为归一化通道相关系数向量h的第i个元素。

4 数值仿真

通过软件接收机[12]对系统校准算法进行仿真，后文如无特别说明，采样频率为典型值62 MHz,中频为46.42 MHz，阵元数目为7，中心阵元为参考阵元，蒙特卡洛仿真次数为500。

4.1 通道校准

在通道校准阶段，校准信号由设备自主产生，校准信噪比可控，在仿真中信噪比变化范围设置为0～10 dB，通道校准中只包含校准信号与热噪声，通道平坦度为3 dB，每次蒙特卡洛实验独立生成一组通道响应。通道校准仿真结果如图3和图4所示。因为阵元4为参考阵元，阵元3和阵元7与其他阵元结果类似，图中只给出了阵元1、2、5、6的统计结果。

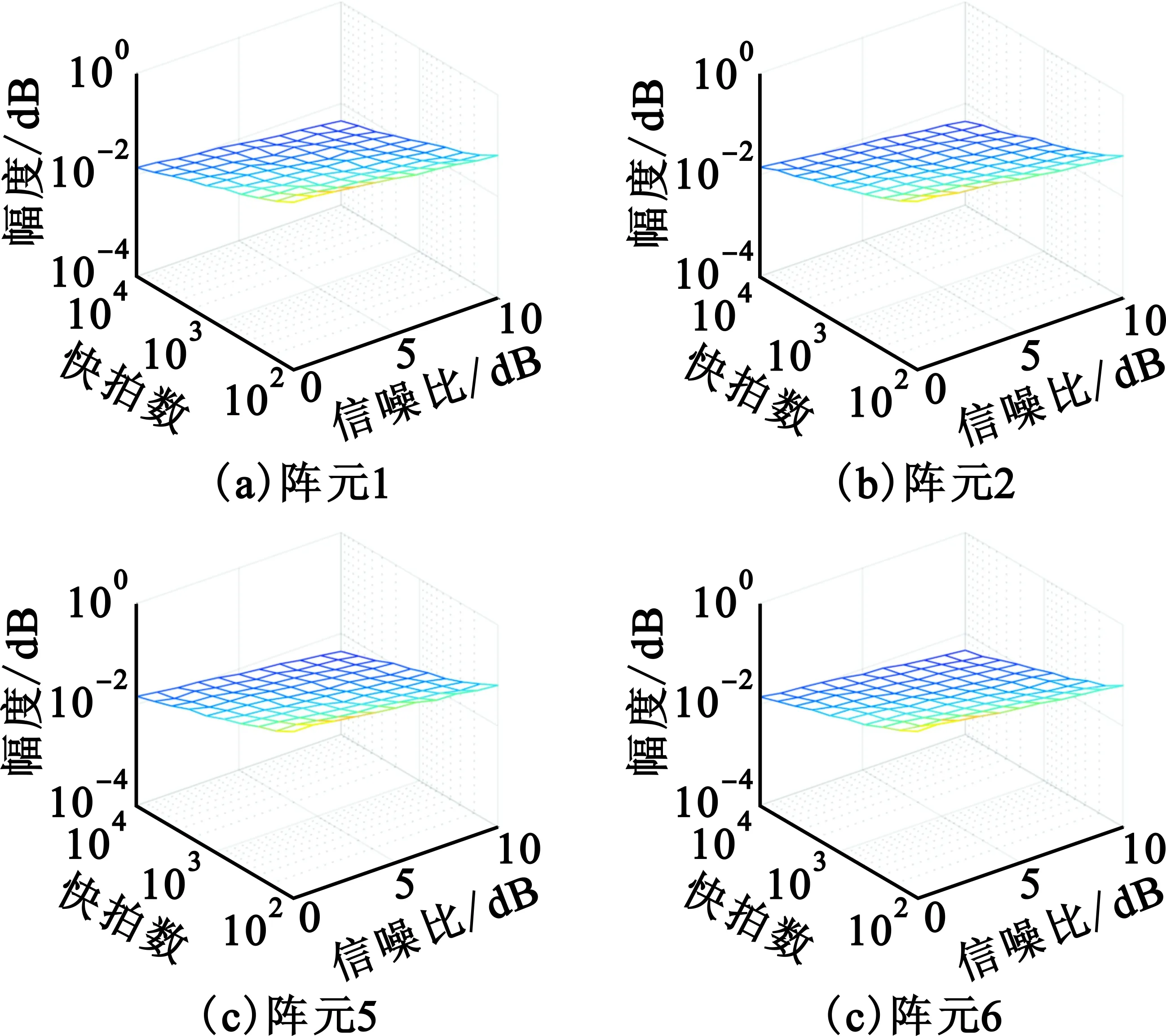
图3 各通道开机校准幅度误差Fig.3 Amplitude error of channel calibration

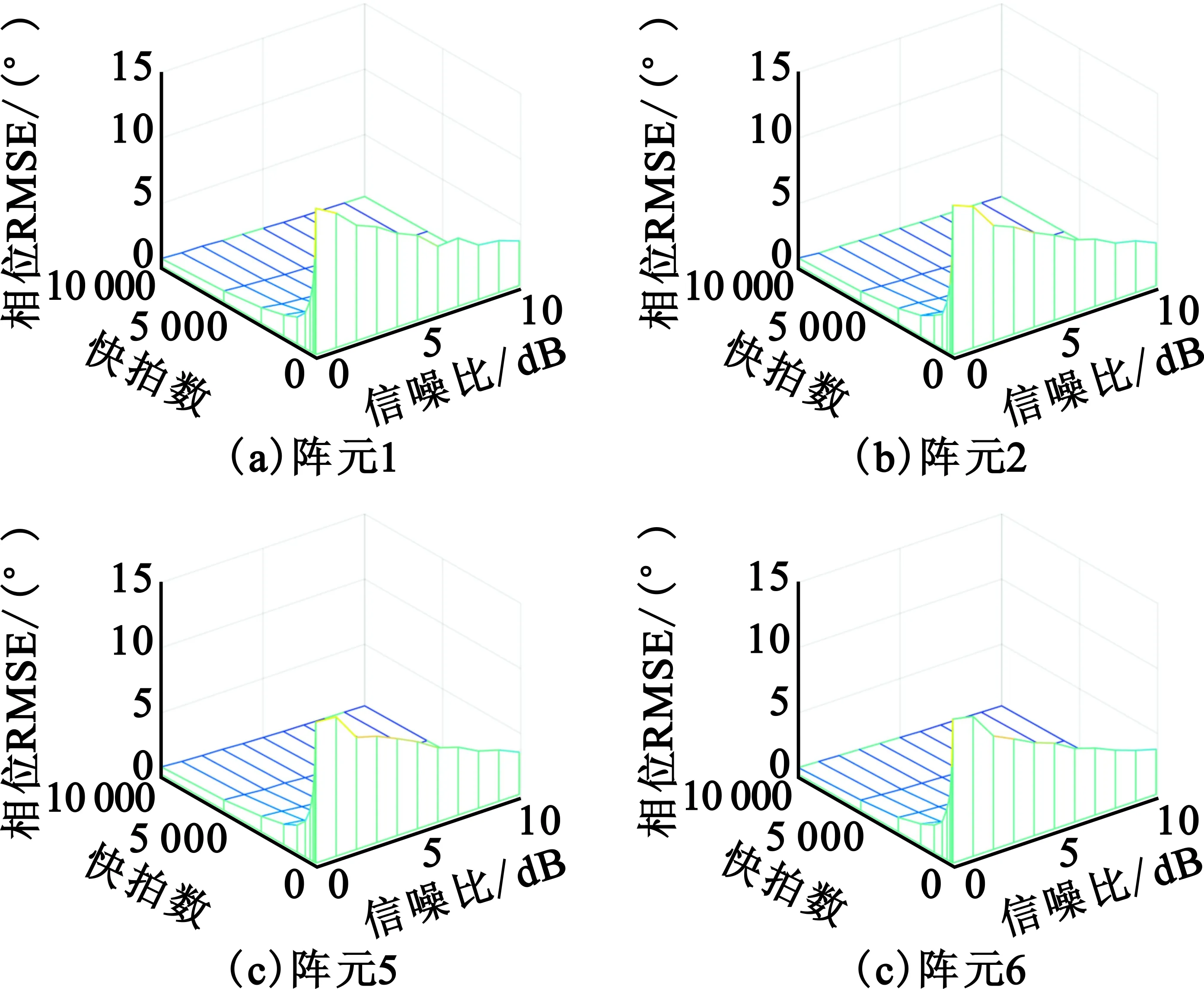
图4 各通道开机校准相位误差Fig.4 Phase error of channel calibration

从仿真结果可以看出，校准结果随着信噪比的提升和快拍数的增加而变得准确。在信号幅度归一化为1时，开机校准的误差在信噪比为0 dB，快拍数104时，校准精度接近10-2，其中，相位的校准误差小于1°。通道校准由设备自主产生校准信号，通过接收通道相关，测量幅相差异的校准算法与传统通道幅相测量算法一致，但是通道校准结果是分离天线现场阵列流形矢量所需，是系统校准不可缺少的一部分。仿真结果给出了工程实践中信噪比和快拍数的选择参考。

4.2 天线校准

仿真场景和通道校准仿真相比，增加了8颗卫星信号。分别对可观测的8颗卫星进行在线测量它们的现场阵列流行矢量，每1 ms测量一次。

图5给出了一组随机校准波束和本文校准波束卫导软件接收机测量的卫导信号载噪比结果，可以看出随机校准波束对于部分卫星信号的跟踪载噪比低于30 dBHz，不能准确地测量卫导信号中的载波相位，无法完成现场阵列流形矢量的测量，而本文校准波束的测量值均大于48 dBHz，能够准确地测量伪距和载波相位，成功地对天线阵列流形矢量进行校准。

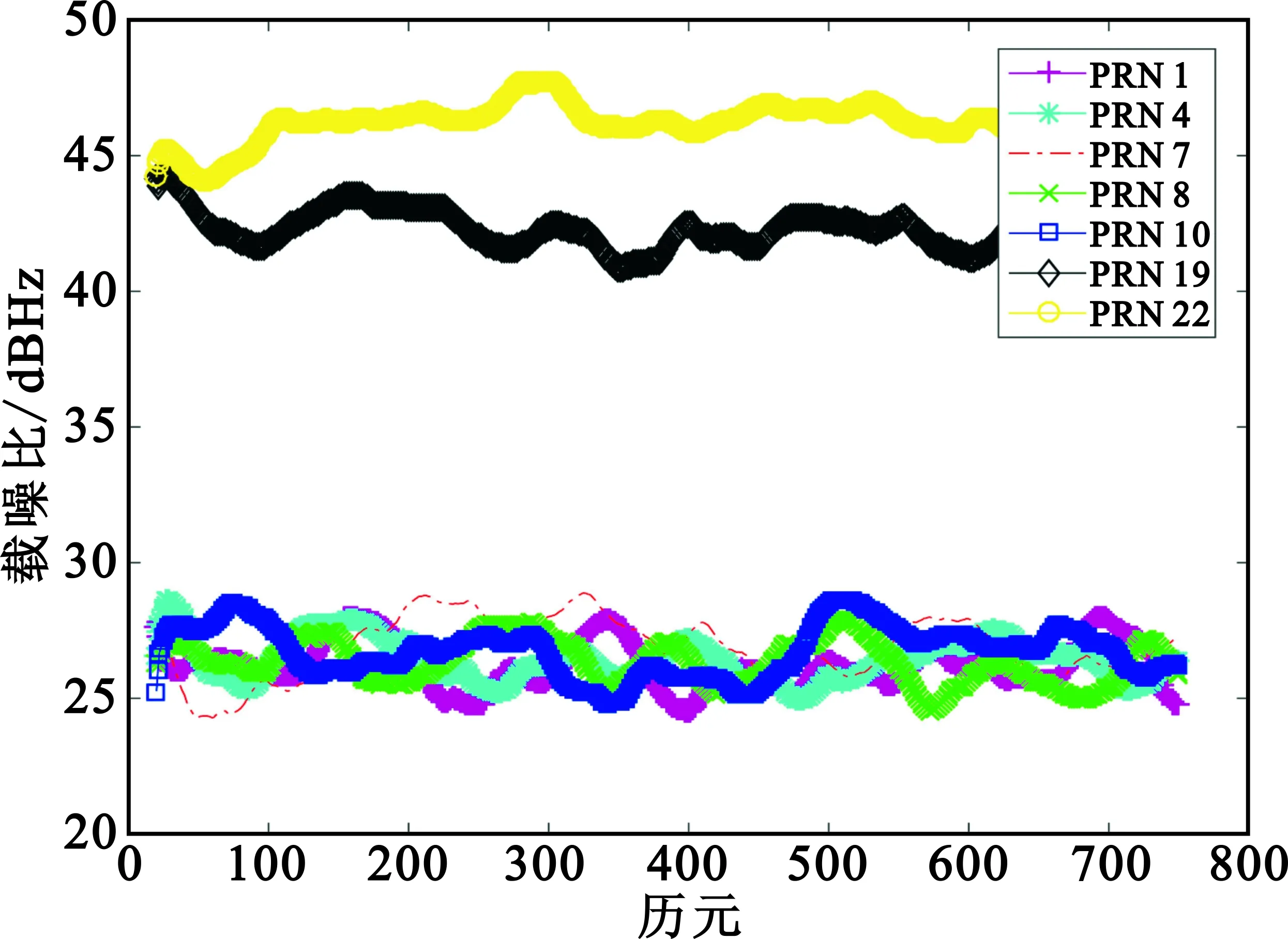
(a)随机校准波束2

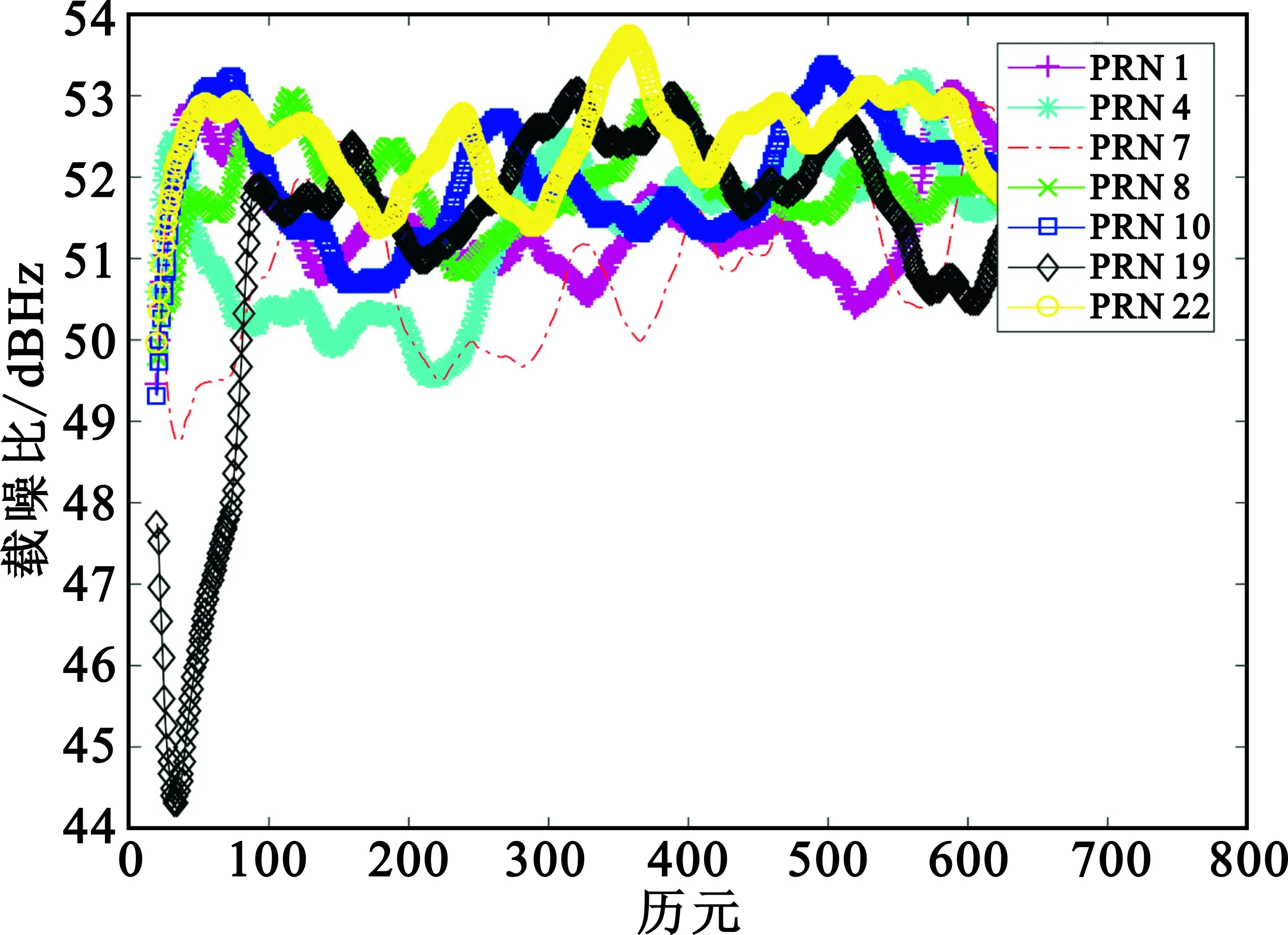
(b)本文校准波束2图5 本文校准波束和随机校准波束接收机载噪比测量Fig.5 Carrier-to-noise ratio measurement of the proposed and the random calibration beams

图6给出了每个历元的测量误差，图7给出了连续100组测量的滑动平均。从图6和图7中可以看出，对于大多数卫星，通过多次在线校准测量值的平均，能够将现场阵列流形矢量的校准误差缩小到2°以内，幅度误差能缩小到0.17 dB以内。

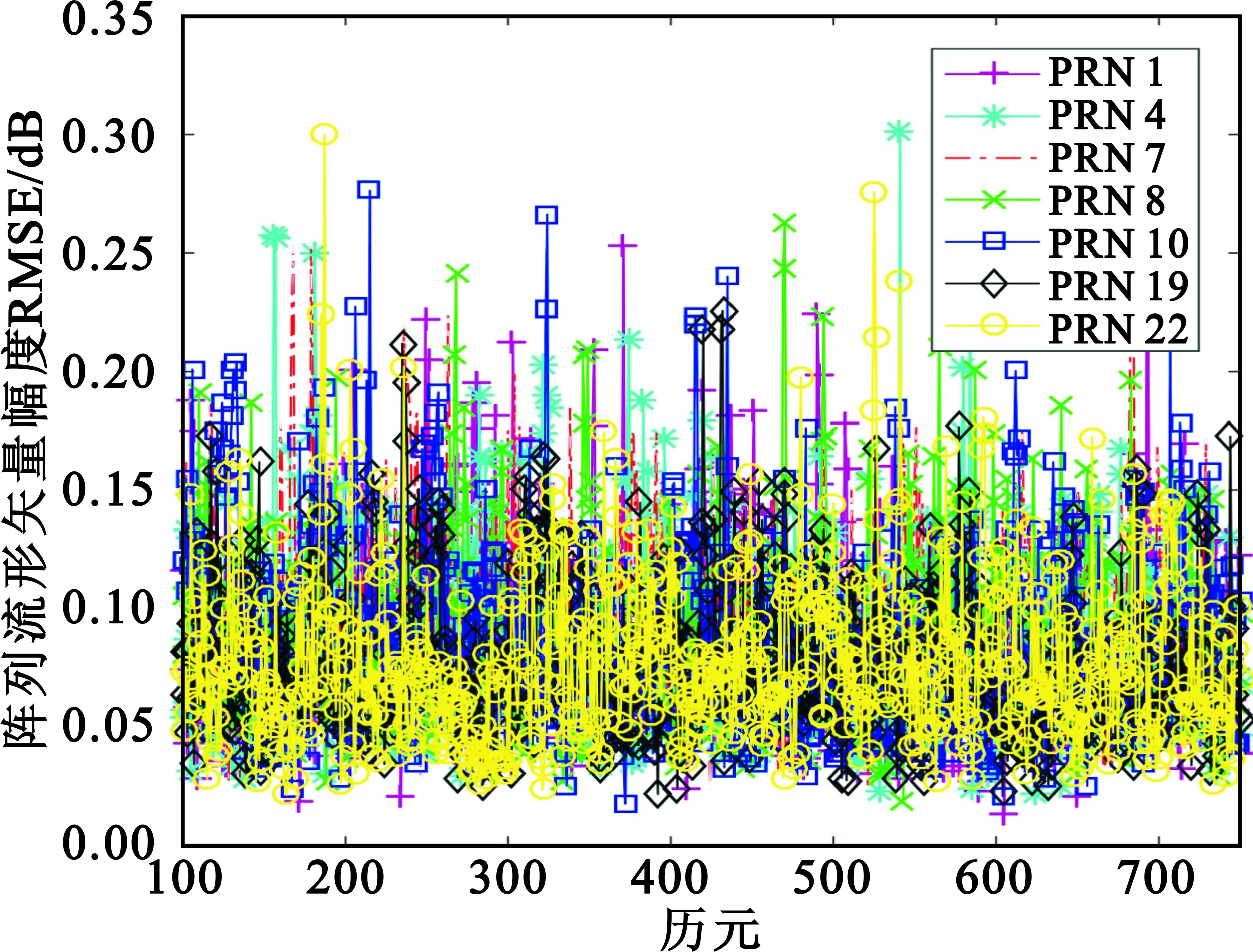
(a)幅度

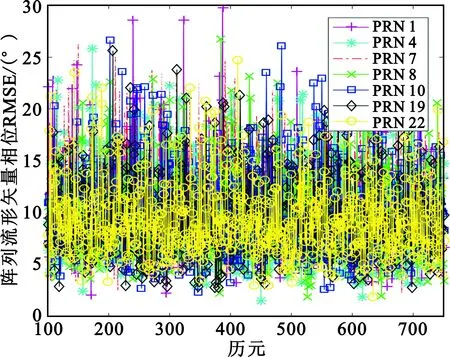
(b)相位图6 现场阵列流形矢量单次测量误差Fig.6 Field array manifold single measurement error

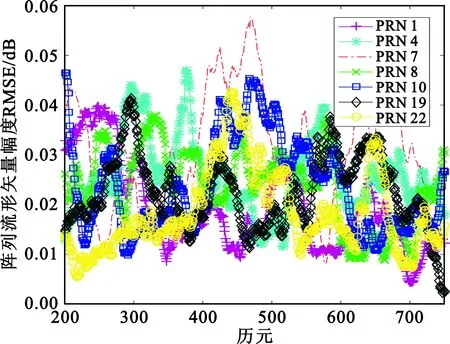
(a)幅度

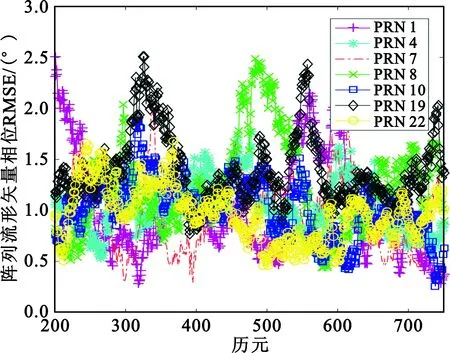
(b)相位图7 现场阵列流形矢量滑动平均测量误差Fig.7 Field array manifold moving average measurement error

从表1中可以看出，随着滑动平均长度的增加，校准误差进一步减小。实际应用中，滑动平均长度100可以满足载波相位差分精密相对定位的需要。与传统幅相测量添加额外参考信号的方式相比，本文方法在性能上具有类似的精度，但是本文方法不需要假设额外的校准信号和测量仪器就能实现现场阵列流形矢量的快速测量。

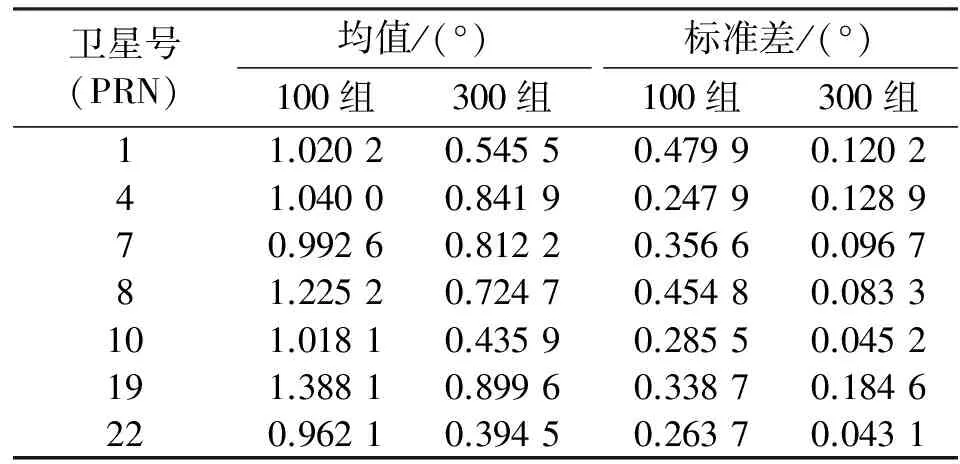
表1 不同滑动平均长度下相位校准统计结果Tab.1 Statistics of different moving average length

5 结束语

本文首先建立了卫导阵列天线接收信号模型，对天线和射频前端引入卫导接收信号的幅相不一致性进行了建模。在高精度差分相对定位应用中，相位不一致性破坏了载波相位测距的假设，将导致定位解算失败。分析表明，控制数字波束形成权矢量的幅度和相位，将直接改变该波束数据中卫导信号的幅度和相位，据此，提出了一种通过规划校准权矢量，结合多通道数字接收机对同一颗卫星信号进行测量，计算该卫星的现场阵列流形矢量的校准方法。同时，结合常规的通道校准方法，对天线的净现场阵列流形矢量进行分离，从而实现了一种易于实现的卫导阵列天线设备的系统校准方法。与现有方法相比，本文重点研究了校准波束的设置，同等条件下提高了校准成功率。本文方法无需外部特定的校准信号，可以简化系统结构和降低系统成本，适合工程应用。在进一步的系统实现中，还需要研究阵列天线的整体流形矢量的表示、与数字接收机的联动数字波束形成、由于多径导致接收机无法正常测量，以及什么样的多径会导致算法失效等问题。

：

[1] KAPLAN E D,HEGARTY C J. Understanding GPS:principles and applications[M].2nd ed. Norwood,MA:Artech House,2006:21-26.

[2] O′BRIEN A J,GUPTA I J,REDDY C J,et al.Space-time adaptive processing for mitigation of platform generated multipath[C]//Proceedings of ION 2010 International Technical Meeting. San Diego,CA:ION,2010:646-656.

[3] COMPTON R T. The relationship between tapped delay-line and FFT processing in adaptive arrays[J].IEEE Transactions on Antennas and Propagation,1988,36(1):15-26.

[4] VAN TREES H L. Optimum array processing:part IV of detection,estimation and modulation theory[M].New York:Wiley-Interscience,2002:1-14.

[5] GUPTA I J,WEISS I M,MORRISON A W. Desired features of adaptive antenna arrays for GNSS receivers[J].Proceedings of the IEEE,2016,104(6):1195-1206.

[6] ZHUANG X B,CUI X W,LU M Q,et al.Analysis of beamforming algorithms for GPS receivers in the jamming environment[J].System Engineering and Electronics,2009,31(3):570-573.

[7] CHURCH C M,GUPTA I J. Calibration of GNSS adaptive antennas[C]//Proceedings of 22nd International Meeting of the Satellite Division of The Institute of Navigation. Savannah,GA:ION,2009:344-350.

[8] XU H,CUI X,SHEN J,et al.A two-step beam-forming method based on carrier phases for GNSS adaptive array anti-jamming[C]//Proceedings of the 2016 International Technical Meeting of The Institute of Navigation. Monterey,CA: ION,2016: 793-804.

[9] 李亚麟,樊讯,胡波,等. 天线校准误差建模及对开环波束赋形技术的影响[J].电讯技术,2010,50(3):1-4.

LI Yalin,FAN Xun,HU Bo,et al.Modeling of antenna calibration error and its impact on open-loop beamforming[J].Telecommunication Engneering,2010,50(3):1-4.(in Chinese)

[10] 曹俊锋,许建文,方云. 接收DBF雷达系统校正技术[J].火控雷达技术,2007,36(4): 63-67.

CAO Junfeng,XU Jianwen,FANG Yun. Correction technology for radar system based on receiving DBF[J].Fire Control Radar Technology,2007,36(4): 63-67.(in Chinese)

[11] 刘宏伟,张守宏. 多馈源空间馈电阵列误差校正[J].电子学报,1999,27(9):105-107.

LIU Hongwei,ZHANG Shouhong. Error calibration for multi-feed array[J].Acta Electronica Sinica,1999,27(9):105-107.(in Chinese)

[12] BORRE K,AKOS D M,BERTELSEN N. A software-defined GPS and Gallieo receiver:a single-frequency approach[M].Boston:Birkhäuser,2007:143-150.