考虑隔夜信息的股市波动建模实证分析
朱鹏飞 唐 勇
(1.福州大学 经济与管理学院,2.福建省金融科技创新重点实验室,福建 福州,350116)
波动率度量一直以来是金融市场研究最重要的中心议题之一。传统的参数法如GARCH类模型和SV类模型仅采用低频数据,无疑会造成大量市场信息的缺失。因此,应用高频数据来度量波动率已获得越来越多人的青睐。其中,以已实现波动(Realized Volatility,RV)为代表的非参数方法在波动率度量领域占据一席之地。然而,已实现波动是把交易时间内日内收益率的平方和作为波动率估计,直接将它用于估计24h连续交易的外汇市场的波动率是合理的,而对于股票市场而言却并非如此。股票交易时间只占全天时间的一部分,然而与股票市场密切关联的各种信息随时都可能发生或发布,从而导致了隔夜信息的形成。由于隔夜信息暂时无法通过场内交易传导或融入市场,所以只能在下一个交易日开盘后得到释放,进而影响当天的股票价格变动。虽然隔夜信息对金融资产价格行为有着重要的影响,但目前学术界对隔夜信息的研究还相对较少。
一、文献综述
Hansen和Lunde[1]525针对以往已实现波动的计算只考虑日内交易信息而忽略隔夜信息,用三种不同方式对已实现波动进行调整,以便对全天波动率进行估计;Tsiakas[2]构建考虑隔夜信息的SV模型,发现对于美国和欧洲的股票市场而言,考虑了隔夜信息之后模型的预测能力得到明显提高,也就是说,非交易时间段积累的市场信息对股票市场有着重要的影响;为了考虑隔夜信息对条件方差的影响,Chen等[3]在GARCH模型的方差方程中加入隔夜收益变量,实证分析表明,隔夜收益对大多数Nasdaq股票的收益率条件方差具有显著的影响;Ahoniemia和Lanneb[4]考察了隔夜信息对S&P500指数和个股的影响,对于指数而言,考虑隔夜信息的波动估计能更加准确地对波动率进行预测,而对于个股而言,考虑隔夜信息后的波动估计并没有提高波动预测能力;Todorova和Soucekb[5]研究了隔夜信息对澳大利亚ASX 200指数和7只高流动性个股波动率的影响,发现隔夜信息能够明显提高波动率的样本外预测能力;Fuertes等[6]分析了成交量、日内收益以及隔夜收益对波动率的影响,发现相比于日内收益、隔夜收益,成交量有助于提高S&P500短期波动率的预测能力。
MIDAS(Mixed Data Sampling)模型是一种常见的高频数据波动模型,以其特有的优点而备受关注,一些学者对其进行了相关研究。Alper等[7]的研究表明,对于波动更强的新兴市场而言,MIDAS模型的预测能力明显优于GARCH(1,1)模型;尚玉皇和郑挺国[8]提出一种包含宏观因子的混频短期利率模型BHK-MIDAS模型,短期利率波动样本外预测方面的良好表现,充分说明宏观因子在识别及预期短期利率波动行为方面的重要贡献。
通过对已有文献研究发现,目前对于隔夜信息的度量,没有考虑隔夜信息融入开盘价的效率问题,很有可能导致隔夜信息度量不准确。另一方面,MIDAS模型权重函数有两种,已有文献对于MIDAS模型权重函数的选择只选择其中一种来进行波动建模,并没有对两者进行比较。因此,本文的创新点和可能的贡献点在于:(1)将隔夜信息融入到开盘价效率度量上,提高了度量的精确程度,提高了本文实证结果的可信度;(2)基于时变的尺度变换因子法对已实现波动进行改良,谋求最佳的波动估计量;(3)选择两种权重函数进行波动建模,并进行优劣比较选择。
鉴于此,本文拟开展以下研究工作:(1)在分析隔夜信息融入开盘价效率的基础上,对隔夜信息(即隔夜收益)度量方法进行修正,以便更为准确、合理地度量;(2)为了考察隔夜信息对波动率的影响,对Hansen和Lunde[1]的尺度变换因子法进行改进,提出了时变尺度变换因子法并对已实现波动进行改进,通过波动建模对4个波动率估计量进行全面的比较,从而选出最优的波动率估计量作为全天波动率的估计;(3)比较不同权重函数(即Beta多项式和指数Almon多项式)对MIDAS模型预测效果的影响。
二、隔夜信息的度量及已实现波动的调整
(一)隔夜信息融入开盘价的效率度量
常用Cao等[9]提出的加权价格贡献法(WPC)度量同一市场不同时段对价格发现的贡献程度,来分析开盘阶段对隔夜信息的揭示效率。第i个时段对日收益rt的加权价格贡献可以定义为:

(1)
其中,rt为t日close-close对数收益,rt,i为t日第i个时段的收益,T为样本期的总天数。价格发现的过程即信息通过交易不断融入价格的过程, 因此某个时段WPC的值越大表明该时段对日价格发现的贡献越大,也即该时段的交易揭示了更多的信息。
(二)沪深300指数不同时段对价格发现的贡献程度分析
沪深300指数覆盖了沪深市场60%左右的市值,成分股为市场中代表性较好的主流投资股票,基本上能够反映市场整体概况,本文选择2011/1/4-2014/7/21期间沪深300指数1min数据作为研究对象,数据来源于WIND数据库。我国股市每日交易4h,为了便于分析,将中午休市阶段看成一个15min。利用式(1)计算出2011-2014年沪深300指数的每15min的WPC值,计算结果见图1(单位:%)。
图1结果显示,2011-2014年沪深300开盘阶段的WPC最大,表明t-1日收盘到t日开盘这段时间对日价格发现的贡献最大,也即开盘阶段的交易揭示了最多的信息。同时,连续交易的第一个15min的WPC仍较大,尤其是2013年和2014年,第一个15min的WPC反而大于开盘阶段的WPC,而从第二个15min开始,WPC快速下降到8%以下,这表明未融入开盘价的隔夜信息在开盘后15min内通过连续交易集中释放。值得注意的是,图中第九个15minWPC,即下午开盘阶段的WPC在1.87%~3.98%之间,远远低于开盘阶段及开盘后15min的WPC,说明中午休市期间公共信息到达的信息量非常小,使得该阶段对日价格发现的贡献程度很小,因此后文研究中不考虑中午休市期间的信息影响。

图1 2011-2014年沪深300指数的15分钟WPC Fig.1 15 minutes’ WPC of Shanghai and Shenzhen 300 Index from 2011 to 2014
(三)隔夜信息的度量修正
(四)考虑隔夜信息的已实现波动调整
Hansen和Lunde[1]530-533最早对已实现波动进行调整以便度量全天的波动率,他们用以下三种方法对其进行调整:

(2)
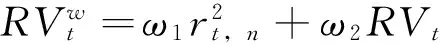
(3)
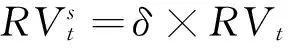
(4)


显而易见,以上三种方法中,对于整个样本区间,隔夜收益的波动与已实现波动率的权重(分别是11,ω1ω2和(δ-1)1)是恒定不变的。然而,在每天的实际波动中,隔夜收益的波动与已实现波动率所占的权重很可能是不同的,因此考虑用移动窗口(rolling windows)的方法,计算每天的尺度变换因子δ,即日内波动在全天波动中所占的比例是时变的,从而有可能更加准确地计算潜在的全天波动率,其表达式如下:
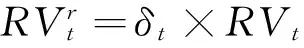
(5)

需要指出的是,式(5)中的RVt与式(2)~(4)中的RVt估计有所不同,式(5)中的RVt估计应除去前15min样本量。
三、波动建模与评价
(一)波动建模
传统的GARCH类模型和SV类模型考虑了波动的聚集性等特征,提高了波动预测精度。然而,这些传统的波动模型都是基于低频数据,没有充分利用丰富的日内交易信息。随着高频数据的易获性和广泛应用,基于高频数据的波动模型成为研究的重点内容之一,这些波动模型可以较大程度地提高了波动预测精度。混合数据抽样(MIDAS)模型的独特之处在于,它允许回归方程左右两边的变量可以按不同的频率进行抽样。
简单的线性一元MIDAS模型的形式如下:

(6)

式(6)中多项式权重函数B(k,θ)是MIDAS模型最重要的组成部分,因为合适的函数形式可以解决参数多和阶数K的选择等问题。目前,对于权重函数的选择主要有以下两种:
(1)Beta多项式
Beta多项式的形式如下:
(7)
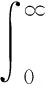
(8)
(2)指数Almon多项式
含有两个参数的指数Almon多项式的形式如下:
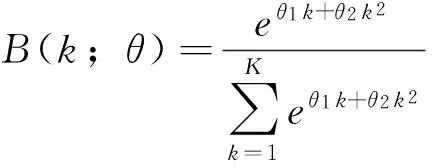
(9)
已有实证表明,采用对数形式进行建模不仅能获得更好的拟合效果,而且在一定程度上也有利于保持模型设定中残差的渐近正态性。因此,本文波动建模都是采用的对数形式:

(10)


(二)模型评价
(1)损失函数法
为了对模型的预测能力进行更为准确的检验,此处的损失函数为损失函数族,其不同于MAE、MPE、RMSE等常用损失函数,形式如下:
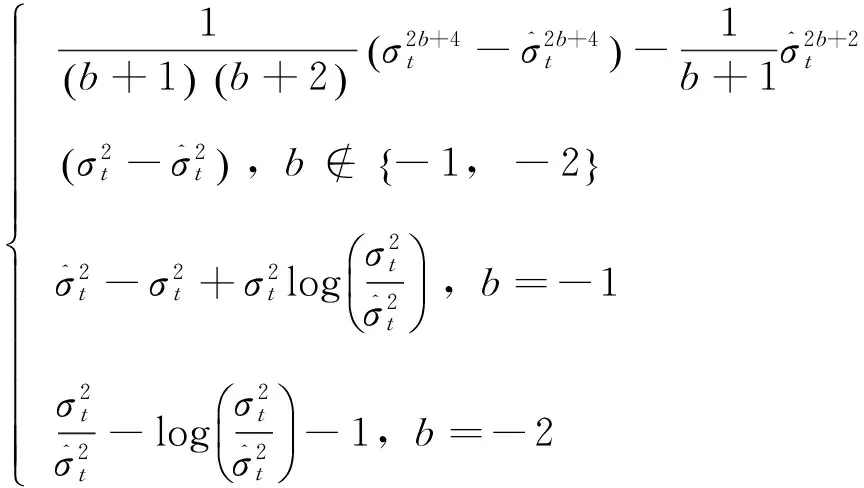
(11)
(2)SPA检验法
除了损失函数法外,另外一种是更为正式的“高级预测能力检验法”(superior prediction ability),即SPA检验法。SPA检验法比损失函数法具有更加优异的模型判别能力,且SPA检验的结论更具有稳健性。限于篇幅,SPA检验的具体过程详见文献[10]。
四、实证分析
此处选取的高频数据与前文一致,抽样频率为5min,使用的软件主要有matlab-2010、Eviews6.0等。
(一)波动率估计量的统计特征

表1 波动率估计量的描述性统计
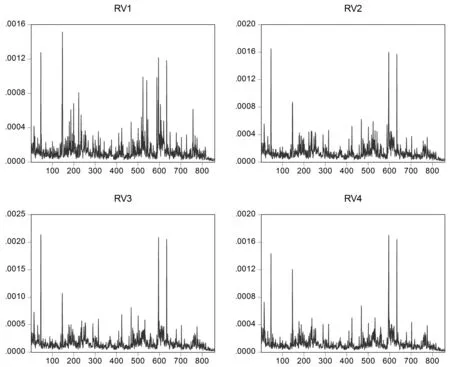
图2 波动率估计量的时间序列图Fig.2 Time series diagram of volatility estimator
一般认为,对数形式的波动率估计量具有更好的正态分布特征,因此,对上述4个波动率估计量取对数,其描述性统计结果如表2所示。从表2可以看出,取对数后,它们的偏度和峰度明显降低,与正态分布较接近,并且J-B统计量也大幅度降低。另外,从图3可以看出,对数形式的波动率估计量的QQ图很接近45度线,因此,可以认为对数波动率估计量近似服从正态分布。

表2 对数波动率估计量的描述性统计

图3 QQ图Fig.3 QQ diagrams
(二)模型参数估计及诊断检验
表3给出了MIDAS模型的参数估计和诊断检验结果,图3给出了各模型的Beta权重图和指数Almon权重图。

表3MIDAS模型的参数估计及诊断检验结果
Tab.3ParameterestimationanddiagnostictestresultsofMIDASModel
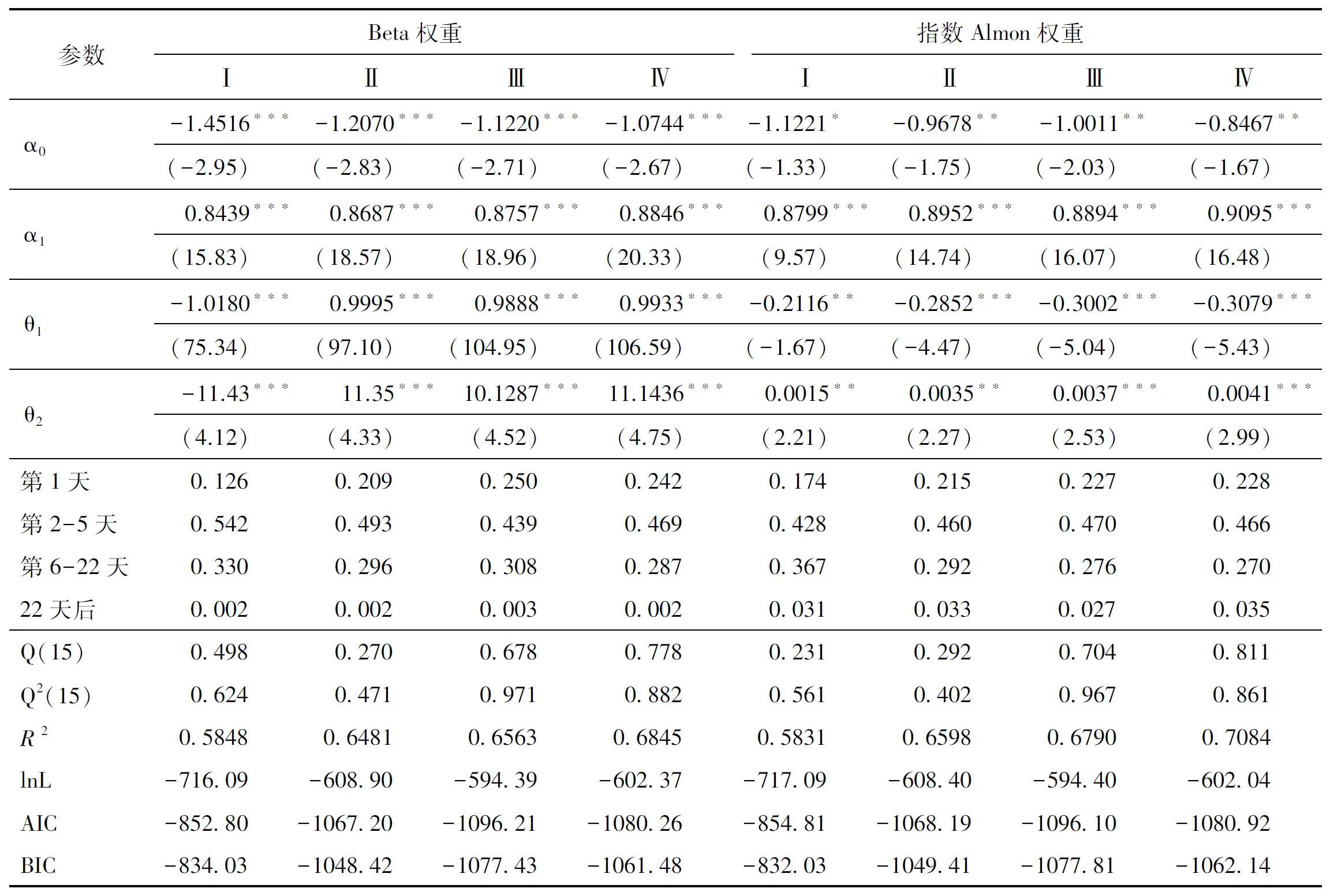


图4 MIDAS模型的Beta权重图和指数Almon权重图Fig.4 The Beta weight diagram of MIDAS Model and the index Almon weight diagram
(三)模型预测评价分析
此处样本总考察区间与前文一致,其中估计样本区间为724d,预测样本区间是134d。为了评价模型的预测能力,首先运用移动窗口法计算各波动模型的样本外预测值,再运用3.2节模型评价方法,分析各波动模型的样本外预测能力。

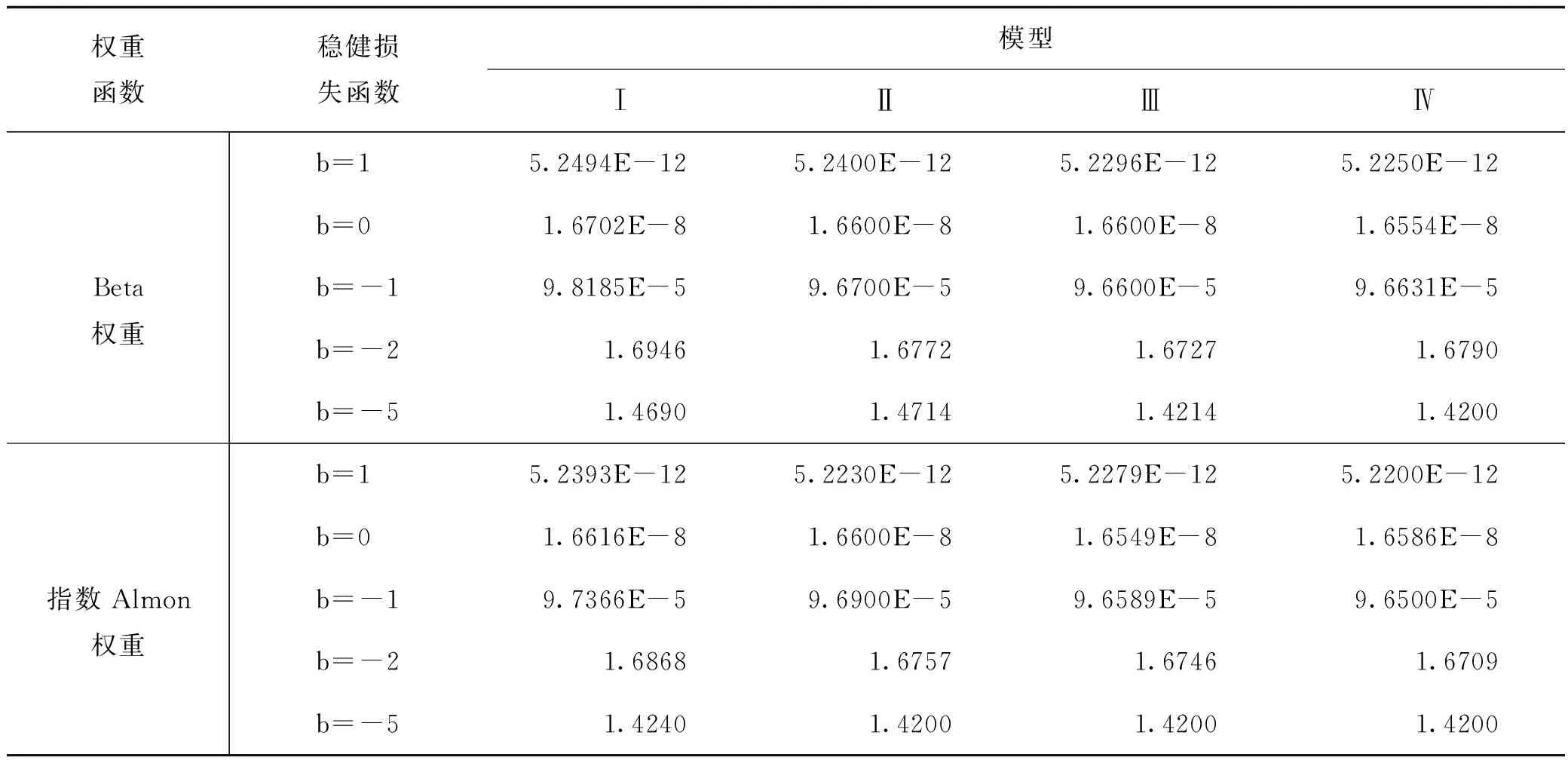
表4 基于五种稳健损失函数的MIDAS模型预测精度检验结果
注:粗体表示的是各损失函数标准下的最小损失函数值。
表5基于SPA检验的MIDAS模型预测精度检验结果
Tab.5ResultsofthepredictionaccuracyofMIDASModelbasedonSPATest

五、结语

总体来看,目前对金融市场隔夜信息的研究还相当有限,一些研究结论远未达到一致性认同。本文基于高频数据视角做了探索性研究,还有相当丰富的内容,期待继续探索下去。
参考文献:
[1]HANSEN P R,LUNDE A. A realized variance for the whole day based on intermittent high-frequency data [J].Journal of Financial Econometrics,2005,3(4): 525-554.
[2]TSIAKAS I. Overnight information and stochastic volatility: a study of European and US stock exchanges [J].Banking & Finance,2008,32(2): 251-268.
[3]CHEN C H, YU W C,ZIVOT E. Predicting stock volatility using after-hours information: evidence from the Nasdaq actively traded stocks [J].International Journal of Forecasting,2012,28(2): 366-383.
[4]AHONIEMIA K,LANNEB M. Overnight stock returns and realized volatility [J].International Journal of Forecasting,2013,29 (4): 592-604.
[5]TODOROVA N,SOUCEKB M. Overnight information flow and realized volatility forecasting [J].Finance Research Letters,2014,11(4): 420-428.
[6]FUERTES A M,KALOTYCHOU E,TODOROVIC N. Daily volume, intraday and overnight returns for volatility prediction: profitability or accuracy? [J].Review of Quantitative Finance and Accounting,2014,12(3): 214-242.
[7] ALPER C E,FENDOGLU S,SALTOGLU B. Forecasting stock market volatilities using MIDAS regressions: an application to the emerging markets [R]. Munich:MPRA, 2008.
[8]尚玉皇,郑挺国. 短期利率波动测度与预测:基于混频宏观-短期利率模型[J].金融研究,2016(11):47-62.
[9]CAO C,GHYSELS E,HATHEWAY F. Price discovery without trading: evidence from the Nasdaq preopening [J].Journal of Finance,2000,55(3): 1339-1365.
[10]杨科,陈浪南.上证综指的已实现波动率预测模型[J].数理统计与管理,2013,32(1):165-179.

