2017年全国数学理科III卷第17题解法分析
——兼谈高考数学对数学核心素养的考查
杨孝斌 潘志坚
(1.凯里学院, 贵州 凯里 556011 2.顺德梁銶琚职业技术学校, 广东 顺德 528300)
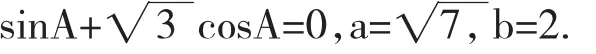
(1)求 c;(2)设 D 为 BC 边上一点,且 A D⊥A C,求△A BD的面积.(注:原题无图.)1.第(1)问之问题分析与解法分析
第(1)问之问题分析:
求什么?——求c,三角形的边长.
有哪些方法可用?——正弦定理、余弦定理、勾股定理、面积法以及c=a·cos B+b·cosA等等.
第(1)问方法 1(用余弦定理):
因为a、b已知,且有关于A的关系式,由余弦定理a2=b2+c2-2b c·cosA知,欲求c只需求角A.

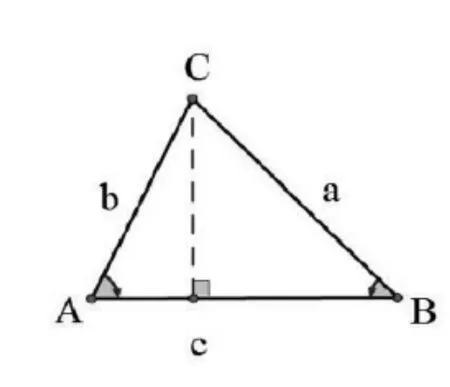
图1
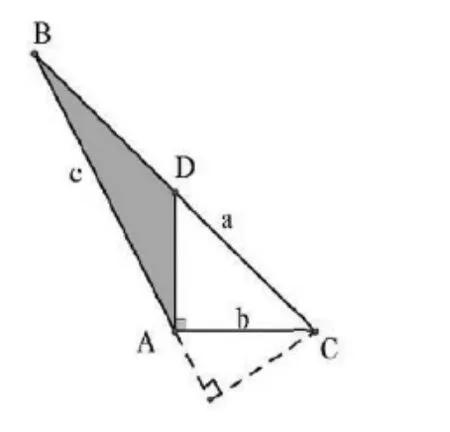
图2
结论c=a·cos B+b·cosA来自于哪里?来自于正弦定理的推导过程(如图1所示),结合此题的实际情况,可作图2.
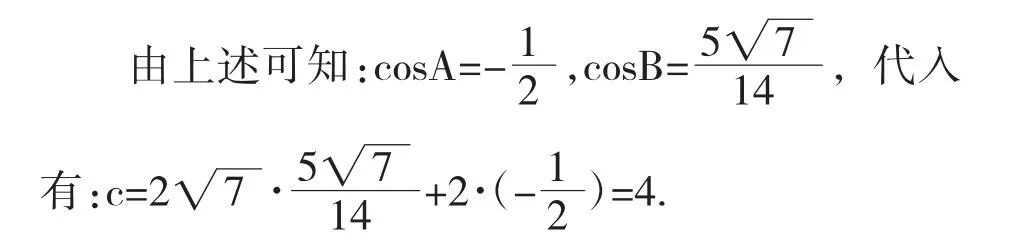
此题第(1)问还可以借助面积法或勾股定理求解,由于在第(2)问要反复用到这两种方法,故不赘述.
2.第(2)问之问题分析与解法分析
第(2)问之问题分析:
求什么?——求△A BD的面积.
有哪些方法可用?——三个三角形之间的面积关系以及各种三角形面积公式.
结合此题的已知条件,构图如图3所示:
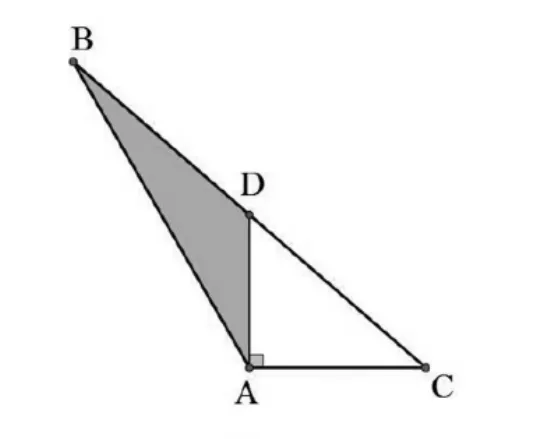
图3
第(2)问方法1(利用三个三角形之间的面积关系):



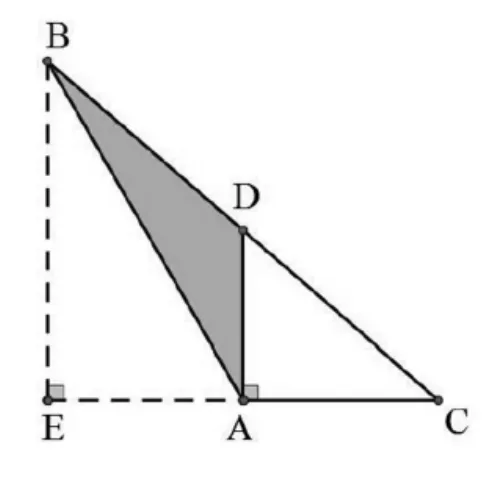
图4

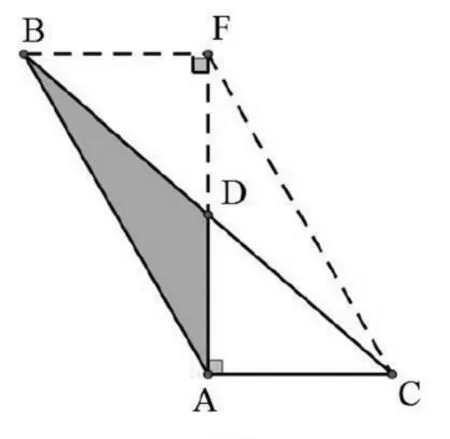
图5

3.该问题的命题立意分析及对数学核心素养的考查
此题为高考数学第一个大题,重在考查考生对正弦定理、余弦定理、勾股定理、角的正弦(余弦、正切的定义)、特殊角的三角函数值、辅助角公式、两角和的正弦(余弦)公式、三角形面积公式、三角形中位线、平行四边形的有关性质、一元二次方程的解法等具体知识的掌握情况,以及对数形结合思想、化归思想、方程思想等数学思想的理解与应用情况.
整体而言,此题知识覆盖面广,难度并不高,上述各种方法均可凑效,在实际考试过程中需要考生迅速的判断出哪种方法更简单易求(如上述第(2)问解法 6、7明显要容易一些,而第(2)问解法4的计算量就要大得多),对考生思维的灵活性有较高要求.在数学核心素养的考查上,此题着重考查了逻辑推理、直观想象、运算能力等方面,同时兼顾数学建模能力、合情推理能力的考查.
逻辑推理对于数学的重要性不言而喻,高考中的几何问题也常常将逻辑推理能力作为首要的考查目标,此题的上述各种解法均涉及逻辑推理.同时,先猜后证是几何解题中的常用方法之一,考生在实际解题过程中可以先猜出D点为BC边上的中点这个结论再进行证明,这就涉及到对考生合情推理能力的考查.
由以上分析可知,题中D点为BC边上的中点这个结论若隐若现.通过上述解法探究,可以认为命题者有可能是将一个完整的直角三角形(如图4所示)或平行四边形(如图5所示)故意残缺而命出此题.考生在解答此题时,若能在对图形的观察中充分把握整体与局部的关系,并将残缺的图形补全,则显得容易得多.这就要求学生具有较高的直观想象能力.
运算能力也往往是高考数学综合题的重点考查目标之一.就此题而言,在运算能力方面重点考查了特殊角三角函数值、一元二次方程的求解、利用正弦定理(余弦定理、勾股定理)进行计算、利用两角和的正弦(余弦)公式进行计算、利用三角形面积公式进行计算,等等.特别地,上述第(2)问方法4,在实际解方程组的时候,计算量相对较大,对学生的计算能力要求较高.此外,方程也是数学模型,因此第(2)问方法4(列方程组求解)涉及到数学建模能力的考查.事实上,从对数学模型的广义理解来看,高考数学综合题常常涉及对学生数学建模能力的考查.

