一种基于基准优选的双目视觉位置解算方法
,,
北京航空航天大学 宇航学院,北京 100083
随着航天活动日益频繁,航天器发射数量不断增加,许多航天器功能失效后滞留于轨道上,严重威胁正常在轨航天器运行安全,对废弃航天器进行轨道移除已经迫在眉睫[1]。在对废弃航天器进行近距离抓捕及轨道移除的操作过程中,废弃航天器相对于任务平台的准确位姿信息对操作的安全性和稳定性至关重要[2],而废弃航天器一般为非合作目标[3],无法主动提供有效的位姿信息,因此需通过在任务平台上安装测量装置,对废弃航天器相对位姿信息进行实时测量[4]。
在非合作目标相对位姿测量方法中,双目视觉以其结构简单、操作方便、实时测量等优点受到广泛研究和应用[5-6]。日本宇航开发局在地面试验中使用双目视觉获取目标卫星图像,并基于三维模型匹配的方法对目标相对姿态进行了估计[7];Segal等建立了基于双目视觉的非合作航天器状态估计系统,并使用扩展卡尔曼滤波算法实现了对航天器相对位姿的测量[8];徐文福等基于双目视觉原理建立了非合作目标位姿测量仿真系统,根据二维图像解算出目标卫星的相对位置和姿态[9];蔡晗等基于双目视觉原理完成了对GEO轨道近距离非合作目标相对位姿测量[10]。对于双目视觉位姿测量而言,关键是在二维图像中提取特征点并进行位置解算[11],而当特征点处于测量域内某些位置时,对其进行位置解算会发生奇异,当特征点处于这些位置附近时,对其进行位置解算会有较大误差,影响后续相对位姿解算精度。
针对上述问题,本文建立了基于双目视觉测量原理的特征点位置解算模型及误差分析模型,分析了特征点位置解算奇异产生的原因,提出了一种采用异面光轴配置和基准优选策略的双目视觉特征点位置解算方法,并通过仿真对该方法的有效性进行了验证。
1 测量原理
本文面向特定的近距离空间操作对非合作目标的测量要求,考虑在任务星上配置双目视觉测量系统,对相对距离在5~10 m范围内2 m级非合作目标上的特征点进行位置测量。
1.1 相关坐标系
1)像平面坐标系Oa-XaYa与Ob-XbYb:原点分别位于a、b两相机光轴与各自像平面交点,X、Y轴在像平面内相互垂直。
2)相机坐标系oa-xayaza与ob-xbybzb:原点分别位于两相机光学中心,x轴、y轴与各自像平面坐标系X轴、Y轴平行,z轴与各自相机光轴重合,指向被测目标一侧。
3)测量坐标系ow-xwywzw:原点位于两相机光心连线中点,x轴指向a相机光心,z轴指向测量前方,y轴根据右手法则确定。
1.2 特征点位置测量模型
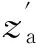
若目标特征点P在a、b相机像面上成像点的像平面坐标分别为Xa,Ya和Xb,Yb,在a、b相机坐标系下的坐标分别为xa,ya,za、xb,yb,zb,在测量坐标系下坐标为xw,yw,zw,则根据透视投影原理[12],有
(2)
相机坐标系oa-xayaza到相机坐标系ob-xbybzb的转换关系可根据双目视觉系统模型得到,其旋转矩阵Cba和平移向量Tba分别为:
Cba=Ly-γLx2θLy-γ(3)
(4)
式中:L为基元旋转矩阵,下标为转轴,括号内为旋转角度。分别以a、b相机坐标系为基准,可解得特征点在相机坐标系oa-xayaza与ob-xbybzb下的三维坐标分别为:
xa=-zaXa/f,ya=-zaYa/f,za=G1/G2(5)
xb=-zbXb/f,yb=-zbYb/f,zb=H1/H2
(6)
G1=fBXbcosθcos2γ-sin2γcos2θ-
fBYbcosθsinγsin 2θ+f2Bcosθsinγcosγ·
1+cos2θ+fBsinθsinγ(-Xbsinγsin 2θ+
Ybcos2θ+fcosγsin2θ)
(7)
G2=-XaXbsinγsin2θ+XaYbcos2θ+
fXacosγsin2θ-XbYa(cos2γ-sin2γcos2θ)+
YaYbsinγsin2θ-fYasinγcosγ1+cos2θ
(8)
H1=-fBXacosθcos2γ-sin2γcos2θ+
fBYacosθsinγsin2θ+f2Bcosθsinγcosγ·
1+cos2θ-fBsinθsinγ(Yacos2θ-
Xasinγsin2θ-fcosγsin2θ)
(9)
H2=XbYacos2θ-XaXbsinγsin2θ-
fXbcosγsin2θ-XaYb(cos2γ-sin2γcos2θ)+
YaYbsinγsin2θ+fYbsinγcosγ1+cos2θ
(10)
相机坐标系oa-xayaza、ob-xbybzb到测量坐标系ow-xwywzw的转换关系可根据双目视觉系统模型得到,其相应的旋转矩阵Cwa、Cwb与平移向量Twa、Twb分别为:
Cwa=Lz-90°LxθLy-γ(11)
Cwb=Lz-90°Lx-θLyγ(12)
分别以a、b相机坐标系为基准,根据式(5)、式(6)所示特征点三维坐标解算结果,结合式(11)~(14),可得到特征点在测量坐标系下三维坐标的两组解算结果,分别为:
(16)
1.3 特征点位置测量误差模型
由双目视觉测量系统模型及式(15)、式(16)可知,测量坐标系下特征点位置解算结果不仅取决于其在像平面成像坐标值Xa、Ya、Xb、Yb,还与测量系统结构参数f、B、θ、γ密切相关。根据来源不同,本文将特征点位置测量误差分为标定误差[13]和观测误差[14],其中标定误差按系统误差处理,观测误差则按随机误差处理。
1)标定误差:若相机像距f、相机光心间距B、相机光轴面内角θ与面外角γ的标定误差分别为Δf、ΔB、Δθ和Δγ,根据系统误差传递及合成理论[15],特征点位置测量标定误差为:
(17)
特征点位置测量综合标定误差

2)观测误差:若特征点P在a、b相机像平面上成像点坐标提取误差分别服从均值为零、标准差为σXa、σYa、σXb、σYb的正态分布[16],根据随机误差传递及合成理论,有
(19)
特征点位置观测误差服从均值为零、标准差为σxw、σyw、σzw的正态分布,综合标准差
(20)
2 解算奇异与基准优选策略
2.1 解算奇异性分析
由式(15)、式(16)可知,当G2→0时,以a相机坐标系为基准进行特征点位置解算时误差激增,当G2=0时,解算出现奇异;当H2→0时,以b相机坐标系为基准进行特征点位置解算时误差激增,当H2=0时,解算出现奇异;当γ=0时,owxwzw平面内所有特征点像平面坐标值Xa=0、Xb=0,此时G2=H2=0,以a、b相机坐标系为基准进行特征点位置解算均出现奇异,故owxwzw平面附近特征点位置解算存在较大误差。
2.2 基准优选策略
为避免以a、b相机坐标系为基准时特征点位置解算同时出现奇异,首先在配置上通过相机错角安装,使面外角γ≠0,在此基础上,定义面向测量域的基准优选指标参数e。
1)测量域内均匀选取足够多的n个特征点;

3)找到n个Ji的最小值Jmin=min{J1…Jn};
4)确定基准优选指标参数e,在满足e 根据基准优选指标参数e,制定特征点位置解算基准优选策略为: 1)当G2≥e且H2≥e时,两组特征点位置解算结果均比较准确,因此取二者平均值; 2)当G2≥e而H2 3)当H2≥e而G2 4)当G2 测量系统结构参数:B=2 m,f=50 mm,θ=5°,γ=3°,像元尺寸u×v=5 μm×5 μm,相机视场角Ω=45°;结构参数标定误差:ΔB=0.01 mm,Δf=0.001 mm,Δθ=2″,Δγ=2″;特征点像平面坐标提取误差的标准差:σXa=0.5u,σYa=0.5v,σXb=0.5u,σYb=0.5v[17]。测量域:测量坐标系下x轴-1.5~1.5 m、y轴-1.5~1.5 m、z轴5~10 m区域。 为便于分析,选取测量域在owxwzw和owywzw截面上的特征点进行仿真,如图2、图3中阴影部分所示,图中L=3 m,H=3 m,d=5 m,D=10 m。对于面外角γ=0的安装形式,取测量域内owywzw平面上特征点进行仿真,结果如图4、图5所示。 当γ= 0时,owywzw平面上yw=0处特征点在以a、b相机为基准进行特征点位置解算时同时发生奇异,如图4、图5中空白区所示,从而使测量系统应用效果受限。如采用错角安装,解算时至少可获得一组较为准确的特征点位置解算结果,以下对错角安装时测量误差进行仿真分析。 设置相机光轴面外角γ= 3°,分别取测量域内owxwzw和owywzw平面上特征点进行仿真。 (1)测量域内owxwzw平面上特征点 测量域内owxwzw平面上特征点分布如图2中阴影部分所示,图6、图7分别为相应的特征点位置测量标定误差与观测误差标准差。 由图6、图7仿真结果可知,由于两相机光轴异面配置,采用单一基准和基准优选策略下进行owxwzw平面内特征点位置解算时均不发生奇异,但后者位置测量标定误差及观测误差的最大值明 显小于前者,且误差大小基本只与测量距离有关。因此,在owxwzw平面内,基于基准优选策略的特征点位置解算优于单一基准的特征点位置解算。 (2)测量域内owywzw平面上特征点 测量域内owywzw平面上特征点分布如图3中阴影部分所示,图8、图9分别为相应的特征点位置测量标定误差与观测误差标准差。 由图8、图9可知,使用单一基准对owywzw平面内特征点进行位置解算可能发生奇异,奇异点附近特征点位置测量标定误差与观测误差均很大;采用基准优选策略对owywzw平面内特征点进行位置解算不发生奇异,位置测量标定误差与观测误差的值均很小,尽管测量域内某些区域位置测量误差存在突变,但变化范围较小,且观测误差本身具有一定随机性,这种突变造成的影响可以忽略。因此,在owywzw平面内,基于基准优选策略的特征点位置解算优于单一基准的特征点位置解算。 1)使用单一基准进行特征点位置解算时存在奇异及奇异点附近特征点位置解算误差过大的问题,通过相机光轴异面配置尽管损失了少量相机公共视场,但能有效防止两基准下位置解算同时发生奇异,从而确保两组位置解算结果中总有一组较为准确。 2)在两相机光轴异面配置的基础上,根据本文所提出的基准优选指标确定方法及基准优选策略,当测量域内特征点的两组位置解算结果差别较大时,能判别出其中较为准确的一组作为特征点位置解算结果;当特征点两组位置解算结果相近时,可取二者平均值作为特征点位置解算结果。该方法解决了特征点位置解算奇异和奇异点附近位置解算误差过大的问题,总体上提升了测量域内特征点位置测量精度。 参考文献(References) [1] NASCIMENTO J M. Hazard evaluation of the space debris in the geo-stationary orbit[J]. Advances in the Astronautical Sciences, 2010,135(3):1835-1841. [2] 赵国伟,张兴民,唐斌,等. 空间绳系拖拽系统摆动特性与平稳控制[J]. 北京航空航天大学学报,2016,42(4):694-702. ZHAO G W,ZHANG X M,TANG B,et al. Properties of pendulum motion of tether tugging system and its stable control[J]. Journal of Beijing University of Aeronautics and Astronautics,2016,42(4):694-702(in Chinese). [3] OUMER N W,PANIN G.Tracking and pose estimation of non-cooperative satellite for on-orbit servicing[C].I-SAIRAS.Turin:European Space Agency (ESA),2012:4-6. [4] 梁斌,高学海,徐文福. 基于结构光的空间大目标特征重构与位姿测量[J]. 中国空间科学技术,2014,34(5):24-31. LIANG B,GAO X H,XU W F. Feature reconstruction and pose determination for large space target based on point structured light[J].Chinese Space Science and Technology,2014,34(5):24-31(in Chinese). [5] 杨海燕,汤国建. 立体视觉系统的目标可见性及测量精度分析[J]. 系统工程与技术,2012,34(9):1889-1894. YANG H Y,TANG G J. Target visibility and measure precision analysis of stereo vision systems[J]. Systems Engineering and Electronics,2012,34(9):1889-1894(in Chinese). [6] 陈伟,陈志明,王惠南. 基于马代数的交会对接相对位姿测量算法[J]. 中国空间科学技术,2015,35(4):76-83. CHEN W,CHEN Z M,WANG H N. Measurement algorithm based on motor algebra for relative position and attitude determination of RVD spacecraft[J]. Chinese Space Science and Technology,2015,35(4):76-83(in Chinese). [7] FUYUTO T,HEIHACHIRO K,SHINICHIRO N. Motion estimation to a failed satellite on orbit using stereo vision and 3D model matching[C].International Conference on Control Automation Robitics & Vision(ICARCV). Singapore:IEEE,2006:1-8. [8] SEGAL S,CARMI A,GURFIL P. Vision-based relative state estimation of non-cooperative spacecraft under modeling uncertainty[C].IEEE Aerospace Conference. Big Sky:IEEE,2011:1-7. [9] 徐文福,梁斌,李成,等. 基于立体视觉的航天器间相对位姿测量方法与仿真研究[J]. 宇航学报,2009,30(4):1421-1428. XU W F,LIANG B,LI C,et al. The approach and simulation study of the relative pose measurement between space-crafts based on stereo vision[J]. Journal of Astronautics,2009,30(4):142-1428(in Chinese). [10] 蔡晗,张景瑞,翟光,等. GEO非合作目标超近距相对位姿视觉测量[J]. 宇航学报,2015,36(6):715-722. CAI H,ZHANG J R,ZHAI G,et al. Relative pose determination for GEO non-cooperative spacecraft under the ultra-close distance[J]. Journal of Astronautics,2015,36(6):715-722(in Chinese). [11] 郝刚涛,杜小平. 空间非合作目标位姿光学测量研究现状[J]. 激光与光电子学进展,2013,50(8):246-254. HAO G T,DU X P. Advances in optical measurement of position and pose for space non-cooperative target[J]. Laser & Optoelectronics Progress,2013,50(8):246-254(in Chinese). [12] LONG H M,GUO H Y,LIANG F,et al. Distance measurement algorithm based on binocular stereo vision [C].Applied Mechanics and Materials 2014. Switzerland:Trans.Tech.Publications,2014:948-952. [13] 赵萍,李永奎,田素博,等. 双目测量系统结构参数理论与试验研究[J]. 机械设计,2013,30(2):64-68. ZHAO P,LI Y K,TIAN S B,et al. Theoretical and experimental research on structural parameters of binocular vision measuring system[J]. Journal of Machine Design,2013,30(2):64-68(in Chinese). [14] 余慧杰,韩平畴. 双目视觉系统的测量误差分析[J]. 光学技术,2007(S1):157-159. YU H J,HANG P C. Measuring errors analysis of binocular vision system[J]. Optical Technique,2007(S1):157-159(in Chinese). [15] 肖志涛,张文寅,耿磊,等. 双目视觉系统测量精度分析[J]. 光电工程,2014,41(2):6-11. XIAO Z T,ZHANG W Y,GENG L,et al. Accuracy analysis of binocular vision system[J]. Opto-Electronic Engineering,2014,41(2):6-11(in Chinese). [16] 张刘,支帅. 双目测量系统目标相对位置误差分析[J]. 红外与激光工程,2014,43(S1):116-122. ZHANG L,ZHI S. Error analysis on relative position of target of binocular measurement system[J]. Infrared and Laser Engineering,2014,43(S1):116-122(in Chinese). [17] 邸男,田睿. 空间机器人双目视觉测量系统精度分析[J]. 载人航天,2017,23(1):76-81. DI N,TIAN R. Precision analysis of binocular vision measurement system in space robots[J]. Manned Spaceflight,2017,23(1):76-81(in Chinese).3 仿真验证
4 结束语

