北斗全球卫星导航系统境外星数据快速回传的路由优化方法
,,,
1. 湖南大学 电气与信息工程学院,长沙 410073 2. 国防科技大学 机电工程与自动化学院,长沙 410073 3. 中国科学院 上海天文台,上海 200030
星间链路(Inter-Satellite Link)技术是全球卫星导航系统的一项关键技术,利用星间链路提升卫星导航系统性能和自主运行能力已成为全球卫星导航系统的重要发展趋势[1]。以GPS为代表的国外卫星导航系统都在积极发展星间链路[2]。中国北斗卫星导航系统在2015年发射的新一代导航卫星上已经具备星间链路功能,并成功进行了在轨试验。北斗卫星导航系统预计在2020年前后建成全球系统。由于全球布站不足,北斗卫星导航系统届时将通过星间链路解决境外星的数据传输和遥测遥控等问题。因此,如何利用星间链路提高数据传输效率是解决北斗全球卫星导航系统运行控制的关键技术之一。
针对星间数传规划及其路由问题,国内外专家学者进行了一定的研究。文献[3]提出了一种基于地面站集中式的导航星座星间路由算法,其中的假设条件是星间链路资源丰富,每颗卫星可以同一时刻与其他多颗卫星建立星间链路。文献[4]和文献[5]应用演化图对导航星座动态拓扑进行建模分析,提出了以最短到达时间和最小跳数为优化目标的路由算法;文献[6]应用有向图理论对指向性星间链路导航网络的信息传输进行描述,并基于Dijkstra算法提出了最早到达路径和最短路径的路由方法;文献[7]综合利用链路调度信息和节点队列信息实现链路调度按需更新,提出一种基于局部队列的最早投递路由算法。这些研究对于解决全星座的通信与测量问题具有参考价值。但专门针对境内境外数据快速回传问题的研究,目前还没有相关文献报道。
本文针对中国北斗导航星座全球布站受限难题,提出了一种基于遗传算法的路由优化方法,从最大回传时延最小和平均回传时延最小两个方面对路由表进行了优化;分析了导航星座星间链路在不同时间的数据传输的路由问题,采用了基于虚拟拓扑的路由算法,将动态的卫星网络拓扑按一定的时间间隔划分为静态的网络拓扑序列进行分析处理。试验结果表明,该方法可以有效解决境外星数据的快速回传问题。
1 问题描述
导航星座中境外星数据快速回传问题的实质是对数据传输路由表进行优化处理,经过优化处理的路由表能够满足境外星数据快速回传的要求。星间数据传输中,星间路由的传输原理如图1所示。
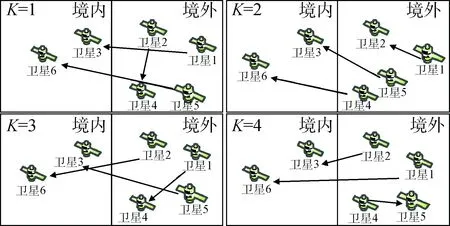
图1 星间路由Fig.1 Inter-satellite routing
在图1中,卫星被划分为境内星、境外星两种属性,其中,境外星上携带一定的数据D,星间的数据传输速度是R,时隙用K表示。以图中境外星2为例,境外星2上的数据D在K=1时隙传输给境外星4,K=2时隙又传输给境内星6,即境外星2上数据D的一条传输路径是(2,4,6)。本文的目的就是找到优化路由表,在任意时刻,根据优化路由表,境外星数据传输回境内星所用时延最小。
上述问题可用以下数学模型来描述:
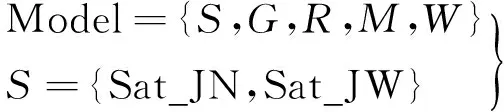
(1)
式中:S为卫星集合,共有N颗卫星;Sat_JN为境内星子集;Sat_JW为境外星子集;G为地面站集合;R为数据传输速率;M为传输任务,即境外星上携带的数据;W为可见性窗口,即导航星座中卫星与地面站的可见时间段。
根据上述模型,总结如下约束条件:
1)建链卫星对之间满足可见性要求;
2)建链表必须是对称的,卫星不与自身建链;
3)同一个时隙中,一颗源卫星只能与一颗目的卫星建立链路。
优化模型可用下列数学表达式描述:
(2)
式中:f0为路由表最大传输时延;K为时隙;Kend和Kstart为数据传输的结束时隙和开始时隙,k为时隙长度,(Kend-Kstart)×k为数据传输时延。f1是整体路由表的平均传输时延,其中:Nn是记录整张路由表传输时延的矩阵。例如N(n)=i1表示目标路由表中,传输时延为n×k的路径共有i1条。
(3)
根据上述的优化模型,可以确定优化函数:
mina×f0+b×f1
(4)
式中:a,b为优化权重。
综上所述,导航星座中境外星数据快速回传重点需要解决两个问题:
1)确定一个合理的优化路由表,按照该路由表建链传输数据时,境外星数据全部传回境内星的时延最小;
2)根据优化所得路由表及星间数据传输速度,明确一种数据传输方案。
2 星间数传模型
卫星网络中的路由可以分为两个部分,星间链路网络路由和边界路由,边界路由解决卫星网络与地面网络之间的融合。一般情况下,若非特殊说明,卫星网络中的路由都是指星间链路网络路由。本文研究的是星间链路网络路由,包括同层卫星网络路由和层间卫星网络路由。基于虚拟拓扑路由算法,链路分配周期是T,每个分配周期划分为多个时隙K。路由表是根据初始规划的建链表和数据传输方向确定的。
2.1 星间链路模型
导航星座选用的是北斗导航星座。根据星地可见性关系将导航卫星划分为境内星和境外星的组合。根据卫星位置,考虑星间距离、天线角度、地球遮挡等约束条件,可以计算星座中卫星之间的相互可见性关系矩阵V=vi,j,Kslot∈RN×N×Kslot。卫星可见性矩阵V如图2所示。
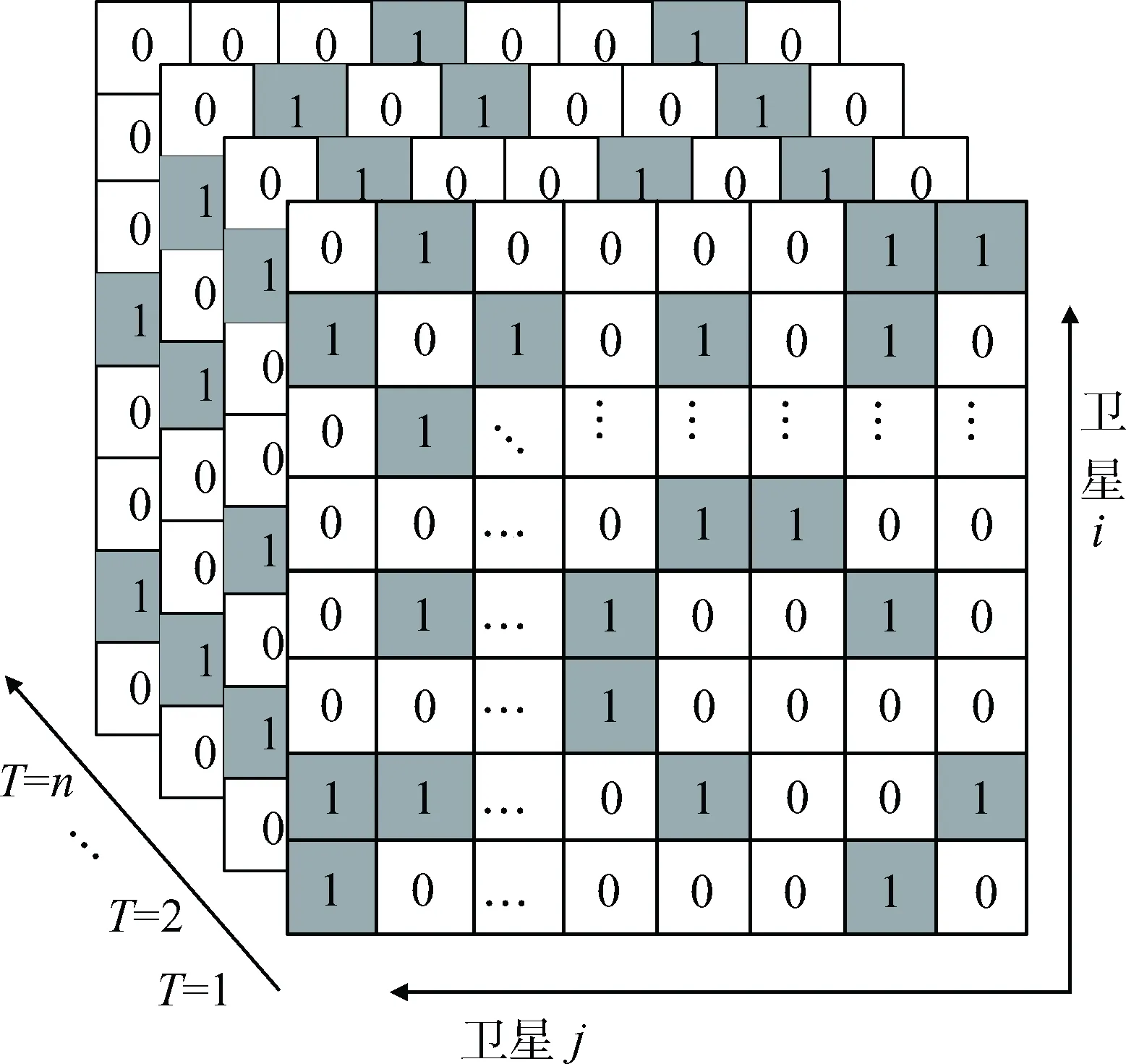
图2 星间可见性关系Fig.2 Inter-satellite visibility relationship
在图2中,每一层矩阵代表一个建链周期的卫星间的可见关系,矩阵中元素为1时表示卫星i与卫星j在该时刻Kslot可见,元素为0则表示两颗卫星之间是不可见。图2中的可见性矩阵生成过程如图3所示。
图3中,T为建链周期,每T/2的卫星数据生成一组初始可见关系,3个T/2的初始可见关系生成一个建链周期T的可见性,相邻两个建链周期的可见性之间存在T/2的重叠时段,有重叠可见性时段的可见性关系生成的路由表,在两个相邻的路由表中,当两个相邻路由表间切换或前一个路由表的A区域向后一个路由表的B区域延展时,可以无需考虑可见性的约束。这种利用重叠可见性的方法生成的路由表,可以有效解决路由表间衔接问题,使得相邻路由表的切换、时隙拓展更加方便合理。
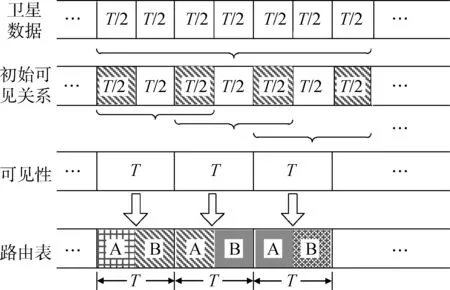
图3 星间可见关系生成过程Fig.3 Generate visible relationships between satellites
根据上述方法生成星间可见性关系,并利用星地可见关系将卫星划分出境外星子集合Sat_JW,以星间可见性为约束条件,进行星间链路分配,生成星间链路分配矩阵B=bi,K∈RN×K。链路分配矩阵B为:
其中bi,K=j,表示卫星i与卫星j在时隙K建立链路。
在链路分配矩阵生成过程中,需要考虑星间可见性、建链表对称性、星间链路数量等约束,约束条件的数学表达式如下:
vi,bi,K,Kslot=1 ∀i,K
(5)
bbi,K,K=i∀i,K
(6)
bi1,K≠bi2,K∀i1≠i2,K
(7)
2.2 星间数传路由模型
路由表作为数据传输路径的走向表,其方向必须要是确定的。本文针对境外数据快速回传这一目标,以境外星到境内星的数据传输方向为准则,形成满足回传目标的路由表。路由表形成规则如下:
1)关闭双向建链表中的境内-境外、境内-境内链路,置零;
2)对于境外-境外链路,随机关闭其中的一个方向,置零。
通过上述关闭规则,可以确定数据传输路由表。如图4中的路由表保证了数据的单向传输,不会发生数据去向不明的情况。例如,在时隙K=1,境外星1将数据传输给境外星2,然后K=2,卫星2将数据传输给境内星1,境外星3将数据传输给境内星2。根据这样的路由表,能够保证每颗境外星上的数据在一定延迟后传回境内星,从而实现境外数据回传境内的目标。
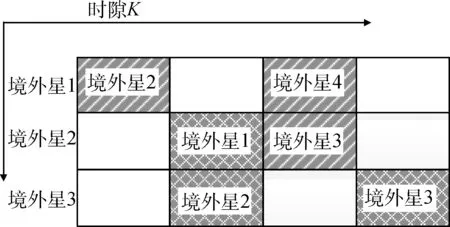
图4 路由表Fig.4 Routing table
3 星间传输路由优化方法
基于遗传算法进行优化计算,得到一个优化路由表,优化路由表需要满足上述路由表的所有约束条件,并且能够满足一定的优化目标。遗传算法的优化步骤如下:
(1)编码方法
本文采用实数编码,一张路由表即一个染色体,每个时隙代表一个基因。
Chrom=[G1,G2,…,GM]
式中:GM代表一个染色体,染色体GM根据第2节中描述的模型计算产生。每个染色体GM的编码为:
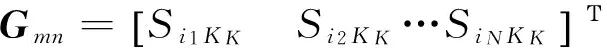
(2)初始化群体
初始化群体方法:对境外星子集Sat_JW中的卫星进行轮询建链,轮询选择时加随机数,避免建链表中链路分配不均匀,由于可见星数有限,建链失败时,将链路置零。按照路由表生成规则,形成算法所需初始种群。
(3)适应度计算
本文在第1节中已经对优化模型进行了阐述。本步骤中的适应度计算就是对上文中优化模型的实现,具体实现方法如下。
假设每颗境外星上携带一个数据,根据路由表,可以计算每个时隙的数据传输流向。传输时延T的计算公式如下:
Ttime=skip×k
式中:skip是跳数,数据每传递一次,就代表一跳;k是时隙长度。某境外星在第m个时隙开始传输数据,在第n个时隙数据传输到境内星,该数据经过n-m+1次传递(即skip=n-m+1)到达境内星完成传输,记录该跳数skip,skip×k就是该境外星的传输时延。筛选出种群中的最大传输时延,将其记为f0。记录了一张表中每个境外星的传输时延,对所有境外星的传输时延求平均值,输出的就是待求路由表的境外到境内的平均传输时延,将其记为f1。
本文中,用于遗传算法染色体的适应度计算函数定义如下:
Ccost=min(a×f0+b×f1)
式中:f0,f1分别对应于第1节中的传输时延;a,b分别对应于优化权重。
(4)选择算子
遗传算法的选择方法有很多,本文中为了避免遗传算法父代个体中的某些个体绝对占优,采用的选择方法是排序法,将染色体的适应度值转变成等差数列,以此作为该染色体的选择概率。
(5)交叉操作
根据前文所述的编码规则,一个路由表即一个染色体,交叉操作就是对两个染色体(父代)中的基因进行交叉,从而得到新的染色体(子代)。本文所用的交叉方法如下:
1)根据适应度函数得到染色体概率值,对概率值排序,根据交叉概率,选取待交叉染色体;
2)待交叉染色体中,采用两两交叉的方法,随机选取一个或多个时隙K,互换两个染色体中K时隙的基因内容,交叉后形成新的子代染色体。
交叉方式如图5所示。

图5 染色体的交叉操作Fig.5 Chromosome cross operation
由于待交叉的路由表是由可见性、境内境外属性等多约束决定的路由表,如果按照简单的随机选取表中元素互换的方法来实行交叉操作,极易造成子代的不合理化,这样极度浪费运算速度,甚至造成遗传算法不收敛等结果。所以本文采用交换整体时隙的内容,这样避免产生的新表中部分数据不合理的情况,使每次交叉后的子代染色体都是符合约束条件的。
(6)变异操作
根据变异概率,对选择出的待变异染色体进行变异操作,本文所用的变异操作是随机选取一个时隙K,对该时隙的路由表进行变异规划。首先对时隙K中境外星的可见星划分优先级,可见境内星优先级大于可见境外星,然后根据优先级进行建链,再用路由表关闭规则,生成时隙K的变异后路由。
4 仿真算例及结果分析
4.1 仿真场景构建
以北斗全球卫星导航系统包含30颗卫星为例。本例中,考虑北斗系统混合星座的特点,30颗卫星按照24颗中轨(MEO)卫星、3颗地球静止轨道(GEO)卫星和3颗倾斜同步轨道(IGSO)卫星的方案(不代表北斗全球系统实际方案)进行分配。每颗卫星装有一部星间链路天线,天线为窄波束天线。卫星轨道参数如表1所示。试验所用到的地面站有北京站、三亚站。遗传算法具体参数见表2。

表1 星座卫星轨道参数

表2 遗传算法参数
为了对算法进行检验,仿真场景的具体参数设置见表3。

表3 仿真场景参数
4.2 仿真结果与分析
根据表3仿真场景进行仿真试验,得到优化路由表,对试验结果进行分析。试验统计了2015年10月1日每分钟的境内星数量,并计算每分钟优化所得路由表的最大传输时延和平均传输时延。境内星数量、最大传输时延和平均传输时延分别如图6和图7所示。
对比分析图6和图7,可知优化结果的好坏与境内星数目有直接关系。当卫星数量大于或等于15颗时,最大传输时延和平均传输时延均收敛到1跳;当卫星数量小于15颗时,最大传输时延收敛到2跳,平均传输时延收敛到1.3跳。
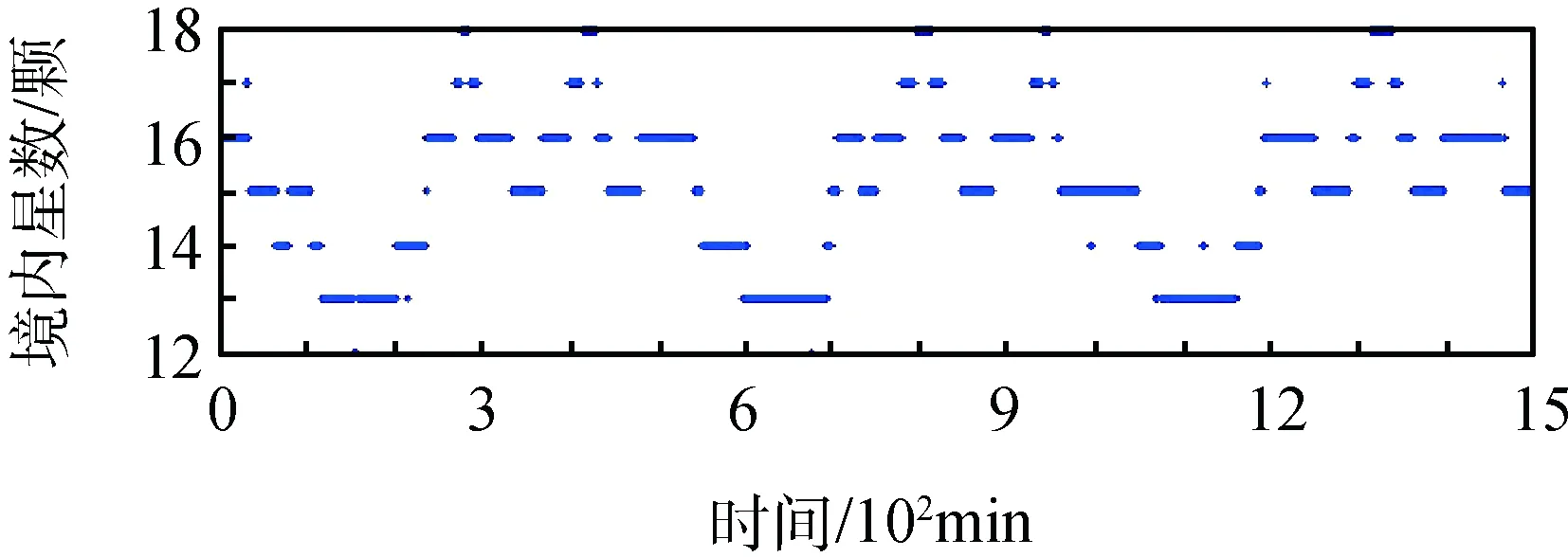
图6 境内星数量Fig.6 Number of domestic satellites
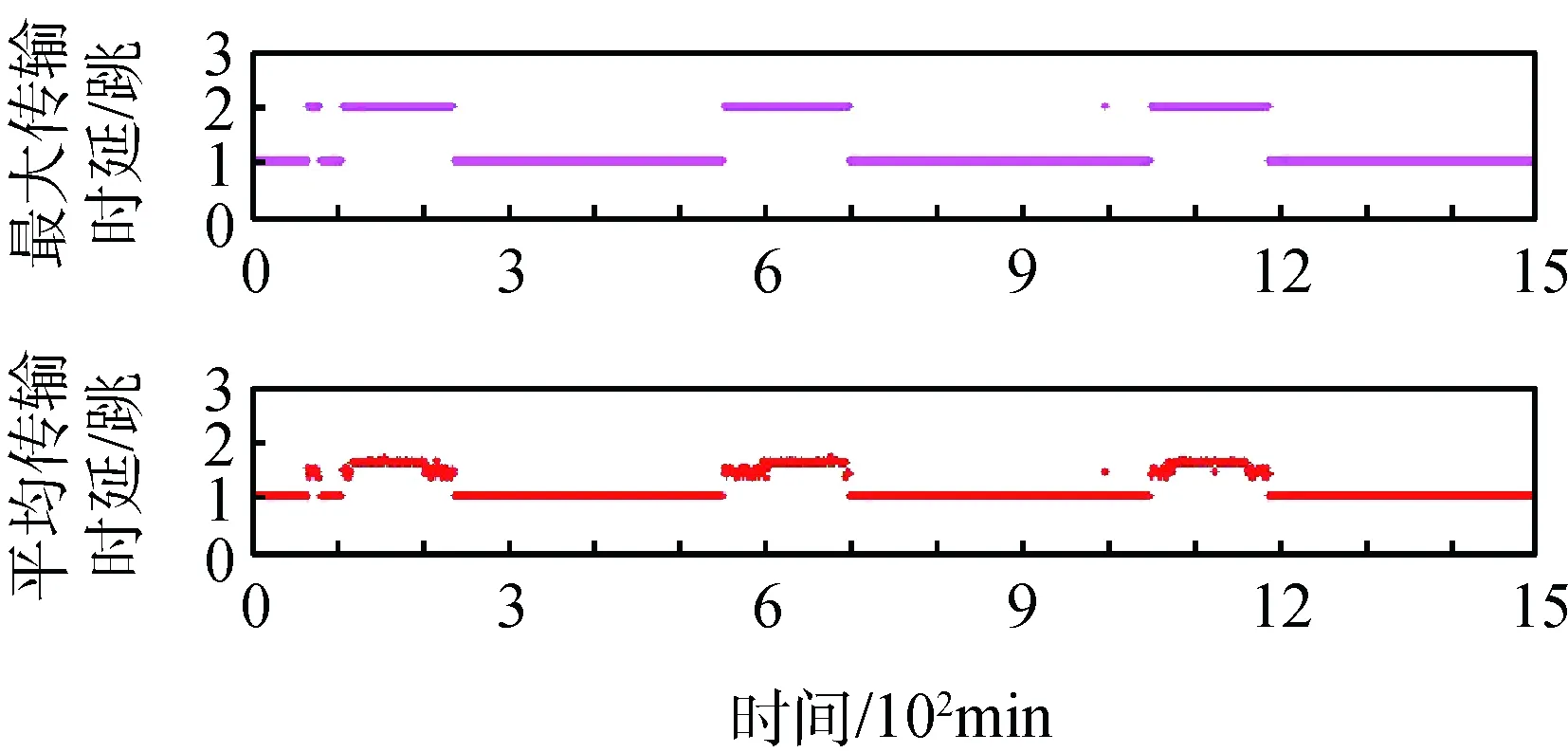
图7 最大传输时延和平均传输时延Fig.7 Maximum transmission delay and average transmission delay
选取两个典型的时刻,分别是境内星数量大于15的第34 s和境内星数小于15的第220 s,假设每次建链传输可以传递的数据量是100 Kbit,每颗卫星上携带的数据量是50 Kbit和300 Kbit,根据两个时刻优化所得路由表,分析数据传输时间,结果如表4所示。

表4 数据传输时间
4.3 算法性能分析
北斗导航星座的24颗中轨卫星(MEO)+3颗地球同步轨道(GEO)卫星+3颗倾斜同步轨道(IGSO)卫星+北京站+三亚站,独立运行20次,遗传算法的收敛性能如图8所示。图8(a)是平均传输时延的收敛性,图8(b)是最大传输时延的收敛性能。从图8可以看出,本文中的算法有着良好的收敛性,多次独立运行均能快速收敛到最优值。

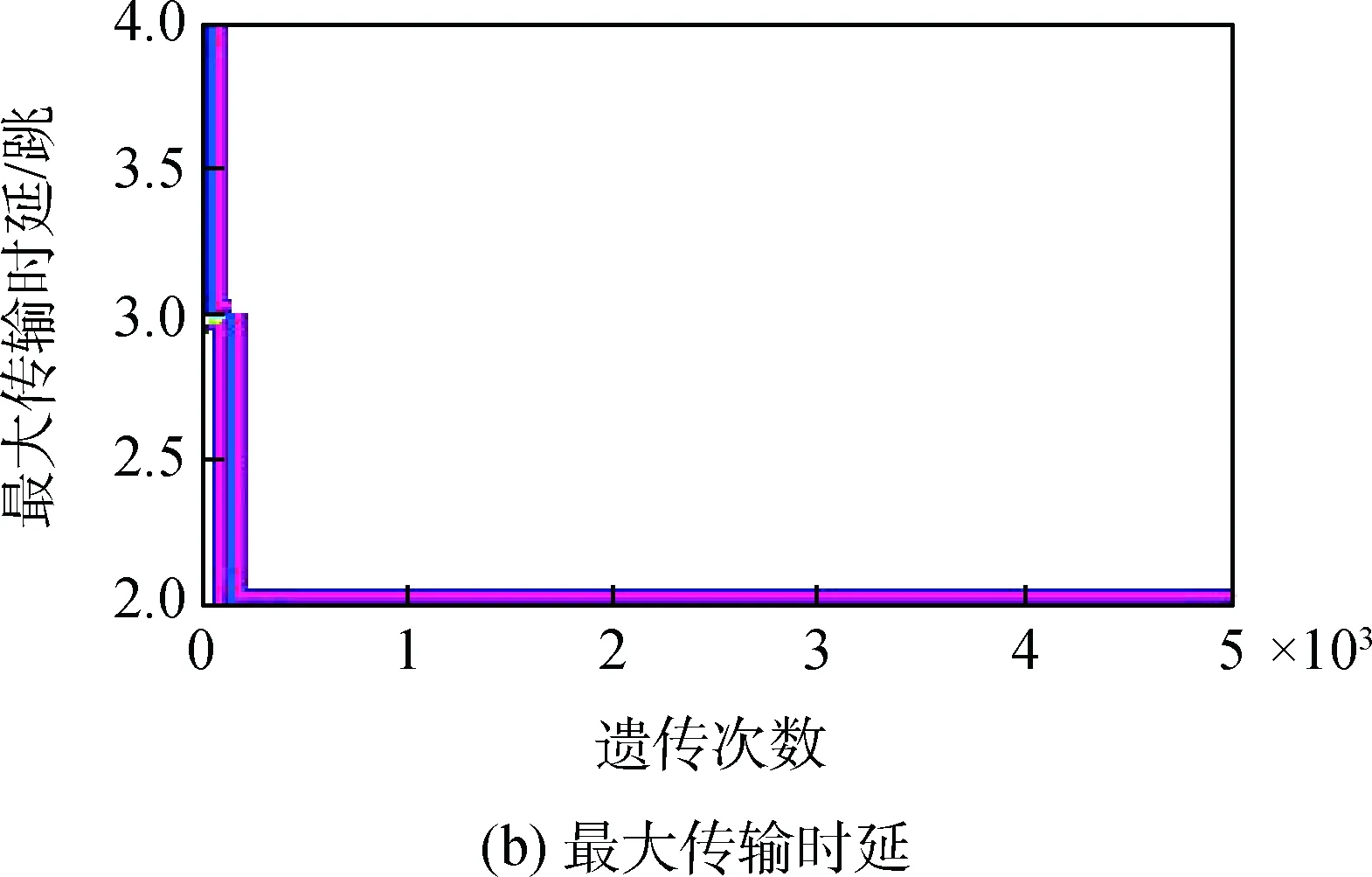
图8 算法收敛性Fig.8 Algorithm convergence
5 结束语
导航星座星间链路是导航星座实现整网数传的重要方法,本文提出基于遗传算法的境外数据快速回传的路由优化方法和数据传输方案,并通过仿真试验,验证了算法的有效性和可靠性。从仿真分析的结果可以看出,针对不同境内星数量,算法均可以优化得到传输时延最优的路由表。
参考文献(References)
[1] MAINE K, ANDERSON P, BAYUK F. Communication architecture for GPS III[C]∥Proceedings of 2004 IEEE Aerospace Conference. Piscataway: IEEE Press, 2004: 1532-1539.
[2] 陈忠贵,帅平,曲广吉. 现代卫星导航系统技术特点与发展趋势分析[J]. 中国科学(E辑:技术科学),2009,39(4): 686-695.
CHENZ G, SHUAI P,QU G J. Technical characteristics and development trend analysis of modern navigation satellite systems [J]. Scientia Sinica,Technologica,2009,39(4):686-695.
[3] 李振东,何善宝,刘崇华. 一种适用于导航卫星星间链路的动态路由算法[C]. 第二届中国卫星导航学术年会,上海:中国卫星导航学术年会, 2011:1.
LI Z D,HE S B,LIU C H. An active routing algorithm for navigation satellite constellation inter-satellite links[C]. The 2th China Satellite Navigation Conference,Shanghai: China Satellite Navigation Conference, 2011:1.
[4] 张之学,薛峰,赵金贤,等. 基于演化图理论的导航卫星星座动态路由准则及算法[C]. 第七届中国卫星导航年会,长沙:中国卫星导航年会2016:6.
ZHANG Z X,XUE F,ZHAO J X,et al. Dynamic routing metrics and algorithms for navigation satellite constellation based on evolving graphic theory[C].The 7th China Satellite Navigation Conference,Changsha: China Satellite Navigation Conference,2016:6.
[5] 王彦,刘波,虞万荣,等. 基于演化图的导航星座星间路由算法[J]. 中国空间科学技术,2012,32(5):76-83.
WANG Y,LIU B,YU W R,et al. Routing algorithm for navigation constellation based on evolving graph model[J].Chinese Space Science and Technology,2012,32(5):76-83.
[6] HOU Z W, YI X Q,ZHAO Y,et al.Information trans-mission path selection of navigation satellite network based on directional crosslink[C]. The 7thChina Satellite Navigation Conference,Changsha:China Satellite Navigation Conference ,2016:461-470.
[7] 燕洪成,张庆君,孙勇. 基于局部队列的导航卫星网络路由算法[J]. 宇航学报, 2015,36(12):1444-1452.
YAN H C,ZHANG Q J,SUN Y. A novel routing algorithm for navigation satellite network based on partial queues[J]. Journal of Astronautics,2015,36 (12): 1444-1452.

