基于支持向量机的卫星执行机构故障诊断研究
,,
南京航空航天大学 航天学院,南京 210016
目前,多颗小卫星协同工作已经成为航天领域发展的新兴方向,也是国内外相关专家研究的最新热点[1]。
小卫星群编队飞行时,成员之间的协同合作以及队形保持等,都要求卫星具备良好的轨道与姿态机动能力,这就需要完备的卫星控制系统与精密的执行机构。在姿态控制系统中普遍使用反作用飞轮作为执行机构,但体积和质量等因素限制了其在微小卫星中的使用。而作为电推进技术之一的脉冲等离子体推力器(Pulsed Plasma Thruster,PPT)可达到与反作用飞轮同样的精度,同时其具有成本低、质量小、效率高,以及结构简单等优点。因此,现阶段微小卫星主要采用脉冲等离子体推力器作为执行机构[2]。
但是,由于卫星工作在环境恶劣的太空中,而且执行机构的工作过程涉及电、热、磁等多个过程,一旦发生故障则会导致执行机构失灵,甚至影响整个航天任务,所以必须保证卫星具备自主故障检测、隔离及故障处理的能力。随着在轨航天器数量的日益增多,航天器的故障诊断技术已经初步形成了比较完善的体系。目前,主要用于故障检测与隔离的方法是基于模型的方法和基于人工智能的方法[3-4]。基于模型的方法主要是在相同的输入情况下,通过构造数学模型与实际系统的输出进行比较生成残差信号,再将得到的残差信号与设定的阈值相比较,从而判断是否发生故障,进一步分析残差信号还可辨识故障的类型。文献[5]利用未知输入观测器,对航天器姿态控制系统的执行机构和敏感器进行了故障检测。文献[6]通过采用扩展卡尔曼滤波技术生成残差,完成了对航天器飞轮的故障检测。文献[7]设计一种鲁棒自适应滑模观测器,利用其对执行机构的故障重构来完成故障诊断。文献[8]以三轴稳定卫星的姿态控制系统作为对象,研究了执行机构故障导致的未知扰动对非线性系统的影响,设计了一组非线性未知输入观测器,生成结构化的残差集,完成对执行机构的故障隔离。然而,对于航天器这种复杂非线性系统,要构造精确的数学模型,存在很多困难。所以,一些专家学者将目光转向了人工智能的故障诊断方法,因其只需要利用已有的历史数据,通过对正常情况下和故障情况下的信息进行训练分析,即可完成故障诊断任务。如文献[9]通过设计一种Mahalanobis-like距离计算神经元间距离的HBF神经网络,并引入新的矩阵表示神经元间的相似度,用于航天器执行机构的故障重构中。文献[10]利用动态神经网络模拟了反作用飞轮的运行特性,实现了对卫星姿态控制系统的故障检测与隔离。文献[11]运用基于遗传算法优化的Elman神经网络故障诊断方法完成了对卫星群姿态控制系统的故障诊断。但是,神经网络模型的准确性通常依赖大量的数据作为训练样本,在历史数据有限的情况下效果将受到影响。同时,神经网络也存在结构复杂,训练时间长,可解释性差等问题。
结合现有的研究成果以及存在的问题,本文对小卫星执行机构PPT系统的故障进行研究分析。首先,介绍了PPT系统及其工作原理和常见的故障情况。然后,提出了一种基于支持向量机(Support Vector Machine—SVM)的故障检测与隔离方案。最后,通过仿真试验,验证了该种故障诊断方法的有效性与快速性。
1 脉冲等离子体推力器
1.1 脉冲等离子体推力器模型
脉冲等离子体推力器作为电推进技术的一种,是微型航天器理想的动力装置[12]。其可应用于轨道转移、位置保持、阻力补偿、精确编队飞行以及姿态控制等许多推进任务。本文通过文献[13]定义的运行特性,对一种类似于LES8/9任务中使用的平行板烧蚀型脉冲等离子体推力器进行研究。其模型如图1所示,主要由电容器、电极板、火花塞、供给弹簧、电流薄片、固体燃料推进剂等部分组成。
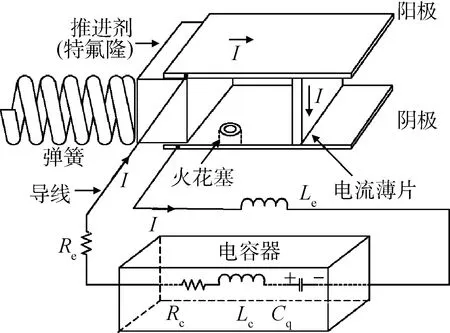
图1 脉冲等离子体推力器(PPT)结构示意Fig.1 Schematic diagram of pulsed plasma thruster
PPT模型的建立有多种方法,这里采用著名科学家Jahn提出的一维数学模型对平板PPT进行建模分析。本文所研究的PPT具体数学模型如下[14]:
(1)
式中:xa为PPT位置信息;xb为电容器电荷量;xc为速度;xd为放电电流;V0为电容器初始电压;ya为推力;yb为放电电流;RT=Rc+Re+Rpe+Rp,LT(t)=Lc+Le+Lpe(t) ,其中
(2)
PPT中其他参数的物理意义如表1所示。
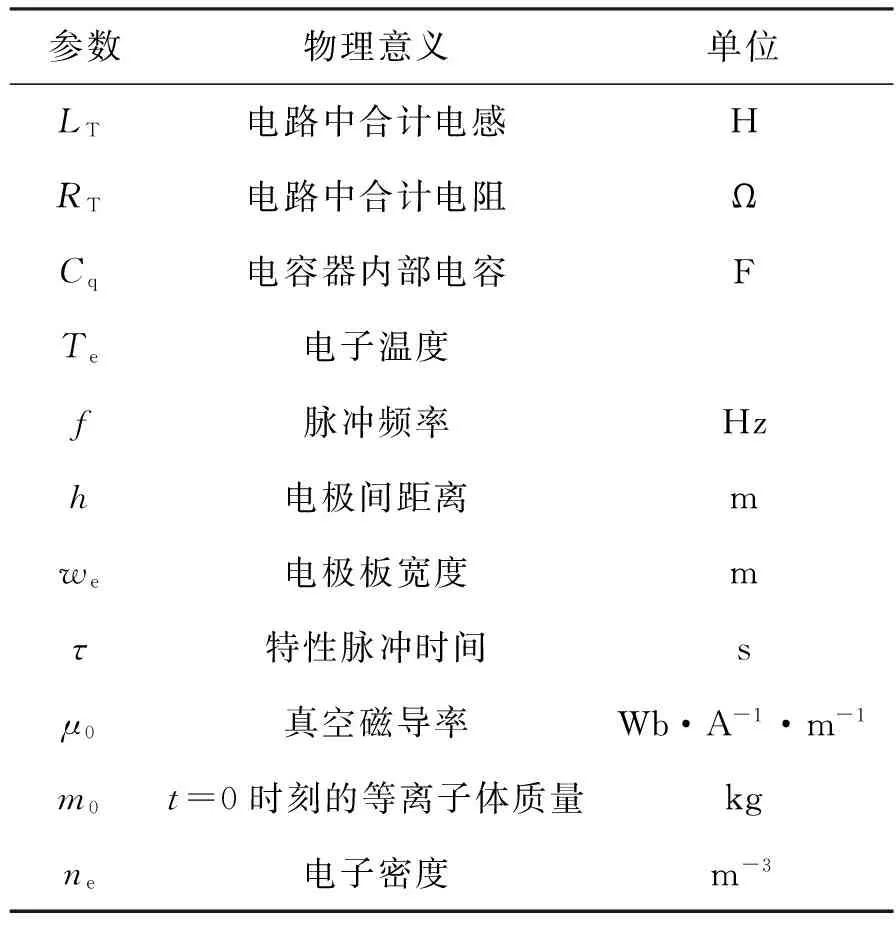
表1 脉冲等离子体推进器模型参数
1.2 脉冲等离子体推力器模型故障情况分析
在实际的应用过程中,由于PPT长期工作在环境恶劣复杂的太空环境中,且随着工作时间的增加,会引起PPT中各电子元器件不同程度的损坏,从而导致其发生故障。严重时会影响到卫星姿态控制系统,甚至导致整个太空任务失败。很多因素,如材料疲劳、废物积累、环境温度影响等,都会导致PPT发生故障。结合文献[14]所提出的问题,本文中主要考虑两种常见的故障情况。
1)推进剂缺失引发的故障。PPT通过周期性的脉冲产生推力,随着工作时间的增加,PPT中的弹簧反复受到冲击载荷的作用,导致其弹性下降,固体推进剂燃料无法被送到正常位置。最终造成推进剂质量m0的减少,PPT产生的推力小于正常情况。
2)导电性能下降引发的故障。在工作过程中,PPT的导线、电极板、电容器等都会受到不同程度的消耗和磨损,一旦某种器件受损程度严重,则会造成其导电能力大幅下降,即电阻RT增加。致使脉冲期间产生的放电电流低于正常值,PPT产生的推力低于容许范围。
由于在实际工作情况中,无法直接测量推力的变化,所以需要通过监测相关电信号变量及其工作温度,判断PPT是否处于正常工作状态。
2 基于小波核函数的SVM模型
2.1 SVM分类器
在故障诊断方面,支持向量机技术相比神经网络、决策树模型、基于模型的方法等效果更好。SVM具有良好的泛化能力、鲁棒性,能够处理带有大量特征的高维数据集。对于神经网络等传统分类器,随着特征数目的增加,效果会下降,引起维数灾难。而对于SVM分类器,学习的复杂性依赖于输入空间的维数,故分类效果不会随着特征数目的增加而变差[15]。
对于N组数据训练点:
(x1,y1),(x2,y2),…,(xn,yn,
xi∈Rd,yi∈±1
yi=w·xi+b(3)
两类数据的支持向量点分别位于平面H1、H2上,
(4)
对数据分类,当超平面离H1、H2几何间隔越远,分类确信度越高,而几何间隔定义为b/‖w‖,由于数据的非线性与空间环境噪声的存在,数据中出现了偏离正常状态很远的异常点,而异常点对于SVM模型将会造成很大的影响。
由于求解b/‖w‖的最大值,相当于求解‖w‖2/2的最小值,通过满足KKT条件,从而转化为对偶问题:
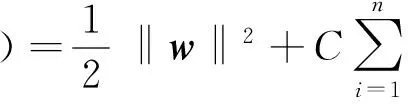
约束条件为:
yi(w·φ(xi)+b)≥1-ζi,ζi≥0(6)
式中:ζi是松弛变量,对应数据点xi最大偏移量;w为超平面法向量;b为截距;C为惩罚参数;n为数据点个数;φ为输入空间到特征空间映射。
这是一个凸二次规划最优问题,避免了直接在高维空间中运算。通过拉格朗日乘子法,令Λ关于w与b最小化,结果如下:
(7)
为了处理线性不可分数据模型,需要把数据特征映射到高维空间,同时在低维空间计算高维映射数据,需要采用核函数k(xi,xj),将非线性可分离数据映射到特征空间使其线性可分。
2.2 小波分析
小波分析作为一种数学工具,能从各种数据中有效地提取所需信息,可通过伸缩和平移对函数或信号进行多尺度细化分析,从而充分展现信号或函数的时频两维特性。
若φ(t)∈L2(R)是可积函数,设其傅里叶变换为H(ω),且满足如下条件(完全重构条件或恒等分辨条件):
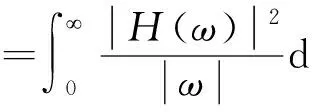
则φ(t)称为母小波函数(Mother Wavelet),通过对母小波函数的伸缩和平移,可得到一个小波序列,即小波基函数。对于连续情况,该序列为:
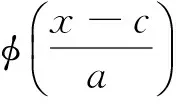
式中:a,c∈R,a≠0,a为伸缩因子,c为平移因子。所以对于任意连续函数f(t)∈L2(R)经过小波基函数分解可表示为:
Wa,c(f)=〈f(x),φa,c(x)〉(10)
其中〈·,·〉表示在L2(R)中点乘的结果。将式(10)重构为:
(11)
(12)
一般的多维小波函数{xj,x∈RN}则是由多个一维小波函数的乘积得到:
(13)
2.3 小波核函数与小波SVM
根据文献[16-20],小波核函数SVM是指将结合了小波分析技术的核函数应用于SVM分类器中。若母小波函数为φa.c(x),xi,xj∈RN,则小波核函数点积结果为:
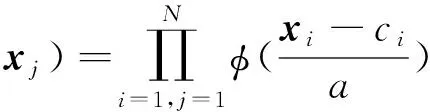
由于脉冲等离子体推进器电流波形与墨西哥草帽小波函数波形相近,所以此处采用墨西哥草帽小波函数作为SVM的核函数,它是一种满足平移不变核理论k(xi,xj)=k(xi-xj)的小波核函数。所以式(14)可以改写为:
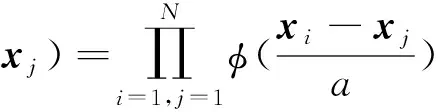
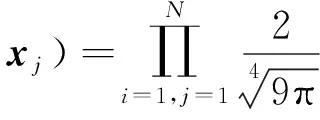
对于该小波核函数SVM的决定函数为:
(17)
在设计好SVM核函数后,利用SVM对脉冲等离子体推力器电流进行拟合预测,还需确定惩罚参数C与核参数a。
2.4 基于自适应遗传算法的SVM参数优化
遗传算法(Genetic Algorithms,GA)是一种有效的全局优化算法,通过借鉴生物界的自然选择和遗传机制,利用选择、交叉和变异等操作,可在大概率解空间中搜索全局中的最优解或次优解。同时标准遗传算法对问题的种类不加限制,不依赖具体问题进行处理。但同时也存在一些缺点,如:1)多次迭代以后,适应度大的个体会占据大多数情况,导致迭代过早结束或多样性减少;2)求解运算时间长,效率较低[21]。故本文采用文献[22]中的自适应遗传算法(Adaptive Genetic Algorithm,AGA),对支持向量机中的惩罚参数C与核参数a进行筛选、优化。由于交叉和突变的适应性概率,AGA可以避免GA的局部最优和过早收敛等现象,在寻找适当的核函数参数方面发挥了重要作用,AGA-SVM参数优化算法流程如图2所示。
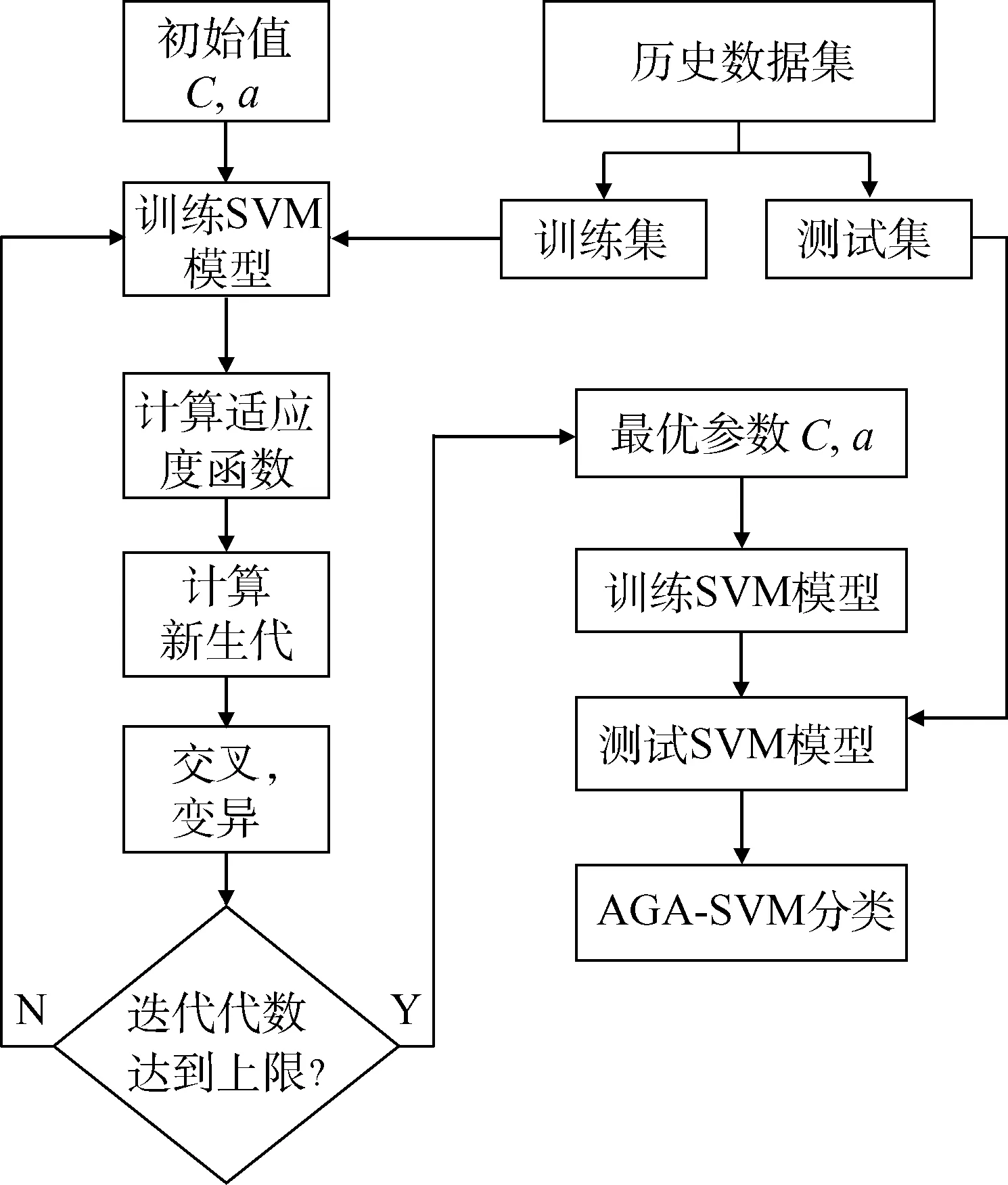
图2 AGA-SVM算法流程Fig.2 Algorithm flow chart of AGA-SVM
3 卫星姿态控制系统执行器故障诊断
脉冲等离子体推进器的工作周期时间较长,样本点信息含量较多,采用墨西哥草帽小波函数作为SVM的核函数,通过自适应遗传算法对核函数参数进行优化,最终解析出最优超平面。最优超平面在高维将原本难以划分的样本点进行分类,从而实现对故障的检测。通过设置多个SVM分类器,可将检测出的故障样本点进行细分,从而实现故障隔离。
针对上文提到的两种PPT常见故障形式,本文采用一对多的SVM故障诊断方法,即对n类故障构造n个二分类器,运用二分类器将每一种故障与其他种类故障分开,故此处构造两个AGA-SVM分类器。SVM1分类器为系统提供初分类,用于判断脉冲等离子体推力器的故障检测,SVM2分类器在系统故障情况下,用于故障隔离,如图3所示。具体步骤如下:
1)用正常情况和故障情况的数据训练得出SVM1的最优超平面,及故障情况1和故障情况2的数据训练得出SVM2的最优超平面,并构造两个规则滤波器用于信号处理。
2)将PPT模型实际工作时产生的放电电流输入到分类器中,得出分类结果,通过规则滤波器1对结果进行检查。若SVM1输出为1,向系统状态输出1,表示系统工作在正常状态;若为-1,将信号送至SVM2进行故障隔离。
3)SVM2对送入的故障信号进行分类,通过规则滤波器2处理分类结果。若SVM2输出为1,向系统状态输出为-1,表示PPT发生推进剂缺失故障;若为-1,向系统状态输出-2,表示PPT发生导电性能下降故障。
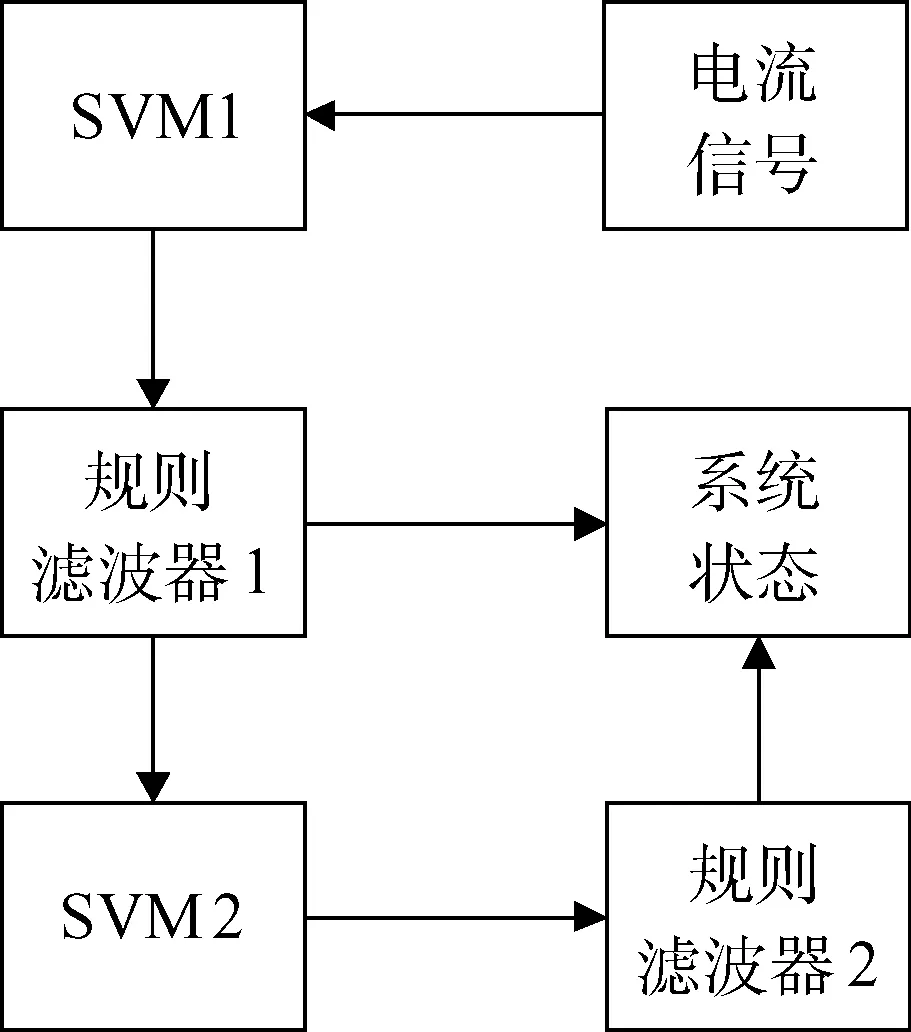
图3 故障诊断系统结构Fig.3 Structure diagram of fault diagnosis system
如果故障较多,对于SVM1分类器的精度要求相对较高,采用自适应遗传算法和小波分析法对SVM1的核函数进行优化,可提高分类的准确性。而之后的故障隔离阶段,为了提高整个系统的快速性,可以不采用遗传算法进行优化。在样本区别明显的情况下,普通SVM分类器也可以达到较高的隔离精度。
4 仿真验证
在仿真试验中,首先根据1中的方法对脉冲等离子体推力器进行建模,各参数数据参考LES-8/9卫星所使用的推力器模型[23]。设置电容器放电周期为1.8×10-5s,初始电容电压910 V。正常情况下10个周期内,PPT的放电电流变化情况和每个周期产生的推力如图4所示,PPT每个放电周期内可产生81 μN的推力。
在故障1情况下,推进剂缺失会导致每个脉冲周期初始推进剂质量m0减少,仿真时将m0的值减小20%。图5显示了故障1情况下10个周期内,PPT的放电电流变化情况和每个周期产生的推力,从图中可以看出PPT每个放电周期内产生的推力下降至72 μN。
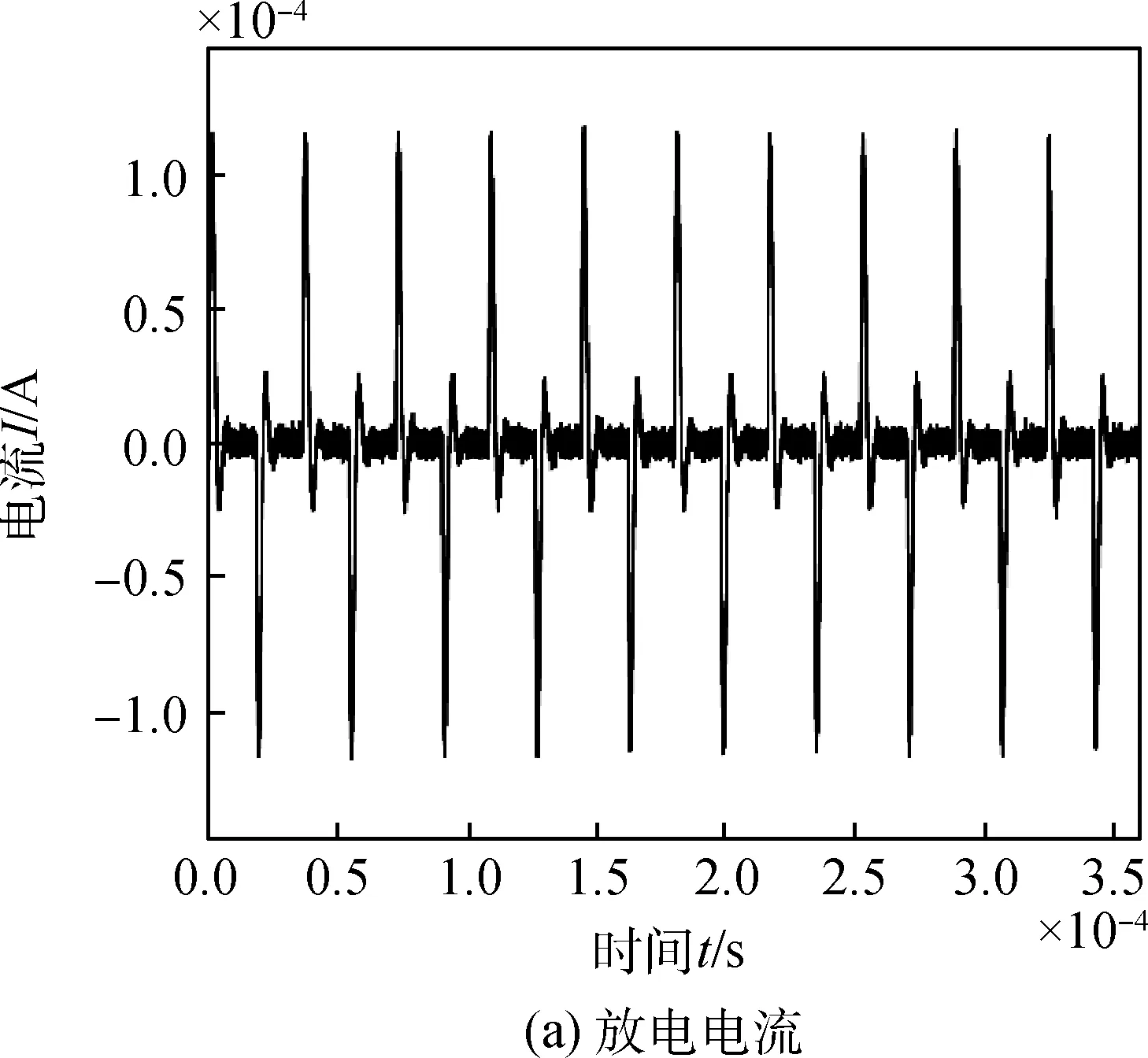
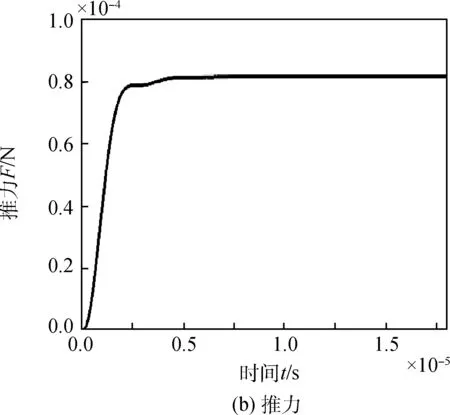
图4 健康情况下PPT放电电流与推力波形Fig.4 Discharge current and thrust of PPTin healthy scenario
在故障2情况下,PPT中电子元器件导电性能下降引发的故障会导致回路中电阻增加,此处针对导线电阻Re增加10%的情况进行仿真。图6显示了故障2情况下10个周期内,PPT的放电电流变化情况和每个周期产生的推力,从图中可以看出PPT每个放电周期内产生的推力下降至69 μN。
SVM完成分类任务,首先要构造样本点,对脉冲等离子体推力器一个周期内的放电电流进行采样,本文在一个周期内采集了4 000组数据,作为一个样本点。由于空间干扰和传感器噪声的存在,在一种PPT的工作状态下,样本点的差异性较大,训练SVM最优超平面需要较多的样本点,故本文选取了400个周期的正常情况放电电流样本点和400个故障情况放电电流样本点(包括200个故障1情况放电电流样本点,200个故障2情况放电电流样本点)作为SVM1的训练数据;400个故障1情况放电电流样本点,400个故障2情况放电电流样本点作为SVM2的训练数据。
因为自适应遗传算法对小波核函数参数的求解是最优可行解,通过求得2个最优可行解,可设计出小波核函数最优参数,从而对较多的训练样本寻找出最优超平面,这个超平面是统计机器学习理论方面的数学最优解。
其中,通过惩罚参数C与核参数对应的决定函数数值与适应度值的关系图可以发现,决定值函数越小适应程度越高,如图7所示。经过自适应遗传算法对墨西哥草帽小波SVM的参数最优化,可得在C=59,a=1.324 5时的墨西哥草帽小波核函数,能够求解出最优的SVM超平面。
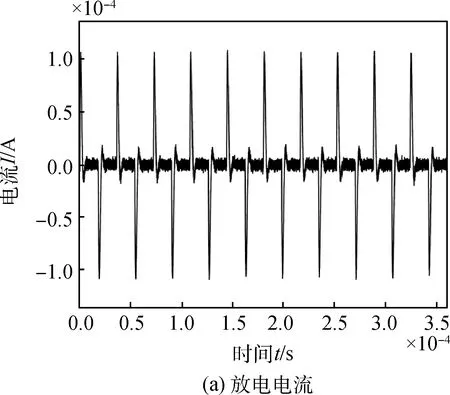
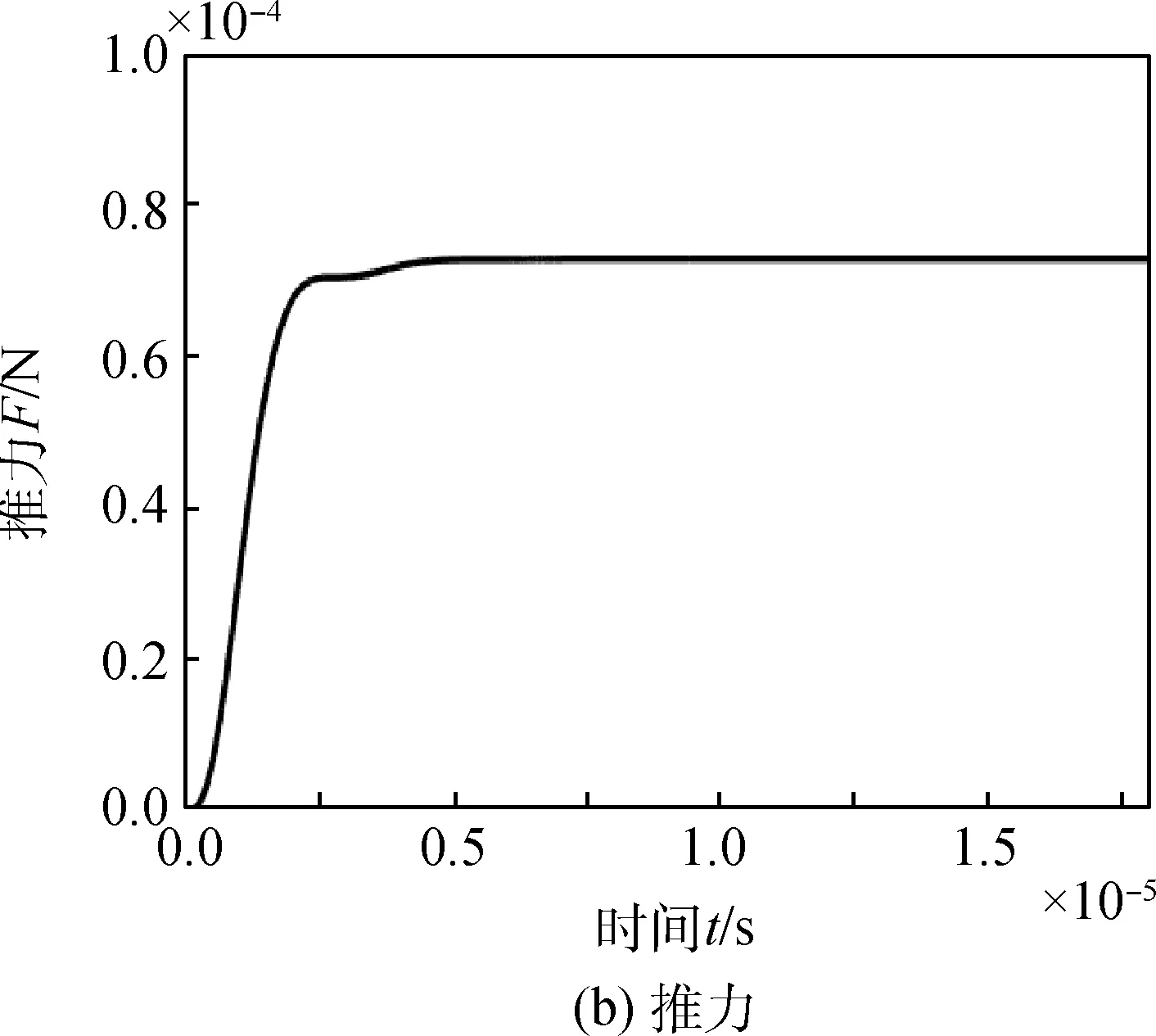
图5 故障1情况下PPT放电电流波形与推力波形Fig.5 Discharge current and thrust of PPTin faulty scenario 1
从理论上看,通过运用求解得到的最优超平面来对实际PPT模型放电电流数据进行故障检测与隔离是可实现的,并且具有良好的泛化能力与快速性。
针对脉冲等离子体推力器的两种常见故障,设计仿真时间为5.4×10-3s,在t=1.8×10-3s和t=3.6×10-3s时分别注入故障1和故障2,在同一时间段内有且仅有一种故障发生。由于每个脉冲周期T=1.8×10-5s,时间极短,故不考虑故障发生于一个脉冲周期内的情况,故障的引入由下一个周期开始。通过300组脉冲等离子体推力器放电电流测试样本点,对运用小波核函数的SVM故障诊断系统进行检测,系统状态如图8所示。
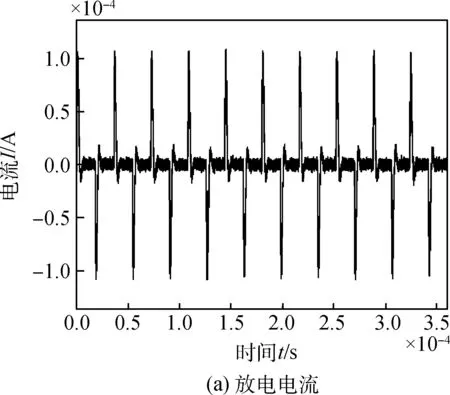
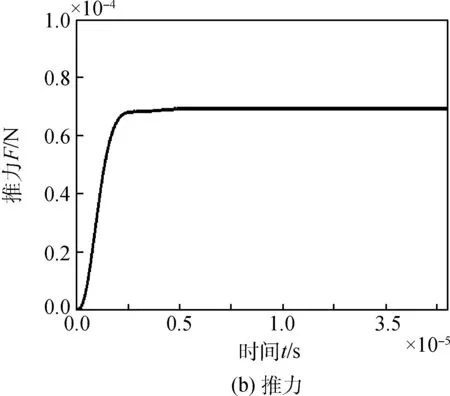
图6 故障2情况下PPT放电电流与推力波形Fig.6 Discharge current and thrust of PPTin faulty scenario 1
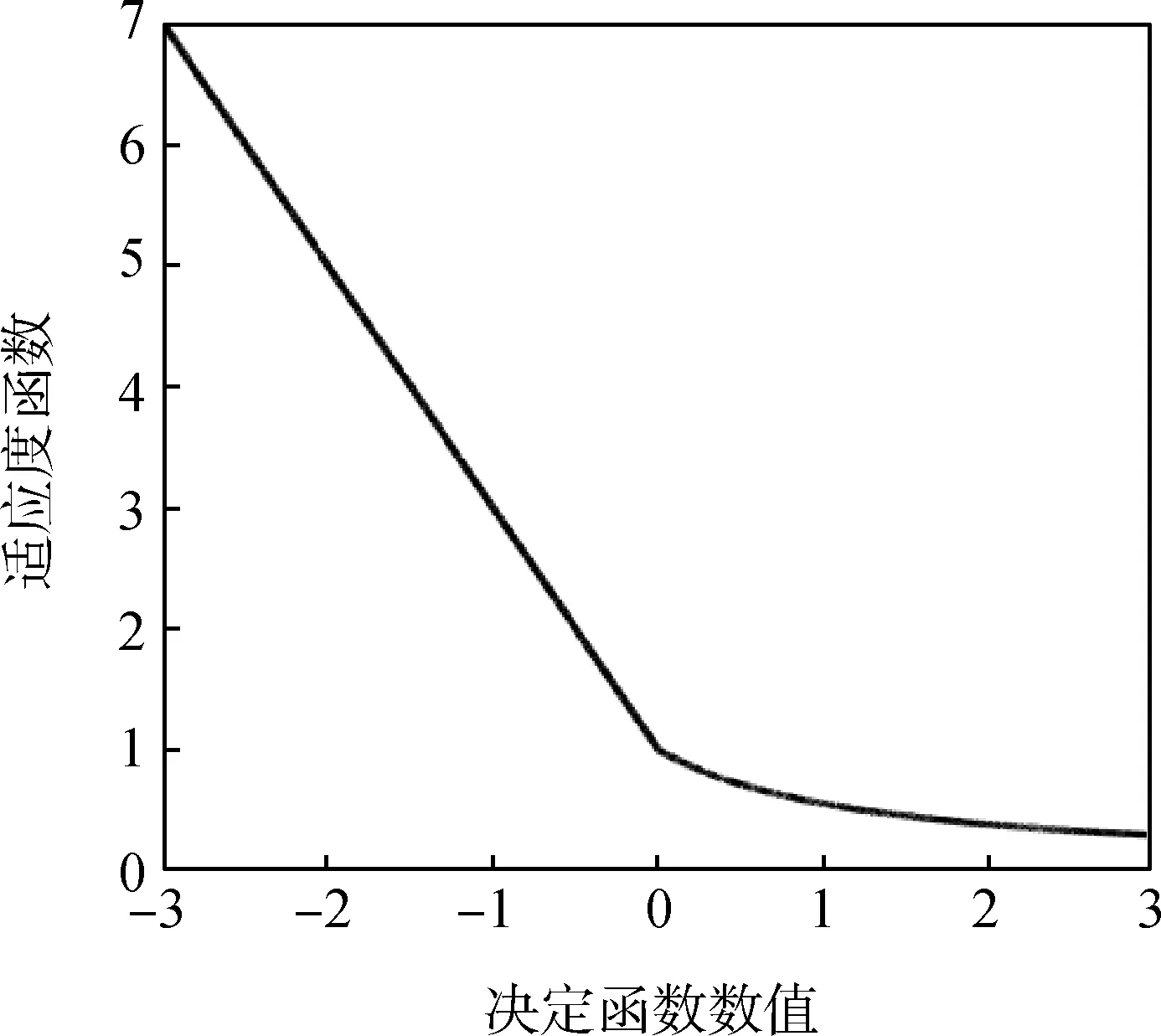
图7 适应度函数与决定函数关系Fig.7 Relation between fitness function anddecision function
从仿真结果可以看出,在前1.8×10-4s内,系统状态为1,证明其工作在正常状态。t=1.8×10-4s时,系统状态变为-1,表示发生了第1种故障,当t=3.6×10-4s时,系统状态变为-2,表示发生了第2种故障,在300组数据中有15个样本点故障诊断发生了错误,检测正确率达到了95%,在加大噪声以后,检测正确率也在90%以上,从而也验证了本文提出的故障诊断策略是有效可行的。
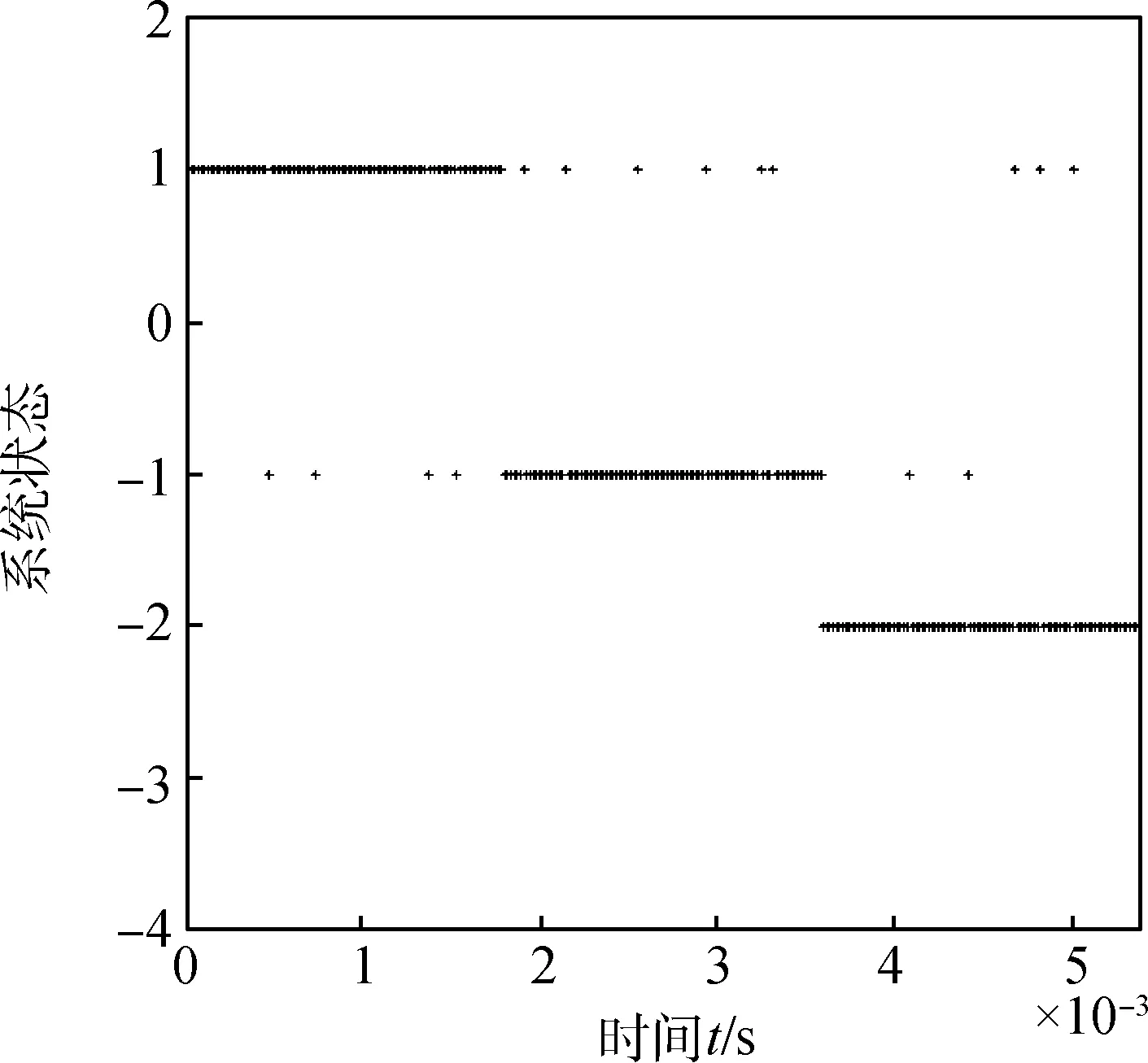
图8 SVM故障诊断结果Fig.8 Result of SVM fault diagnosis
5 结束语
针对脉冲等离子体推力器作为执行机构的微小卫星控制系统故障诊断,本文采用了支持向量机技术对故障进行检测与隔离。在SVM分类器中,添加了小波分析环节,并且应用了适合脉冲等离子体推力器电流波形的墨西哥草帽小波函数作为SVM的核函数,通过自适应遗传算法优化核函数参数,提高了SVM的分类效率与泛化能力。通过选取两种常见的脉冲等离子体推力器故障,进行了仿真试验。仿真结果表明,本文设计的故障诊断方案能快速准确地检测到故障的发生,并确定故障类型。也验证了小波SVM技术在故障诊断方面的快速性与有效性。同时,本文在故障设置方面选取了两种故障分别发生的情况,但没有考虑到两种故障同时发生的情况。并且微小卫星往往以编队形式执行任务,需进一步考虑小卫星编队飞行的故障诊断策略,这些也是未来工作的研究方向。
参考文献(References)
[1] 闻新.太空探索正在进入航天器集群时代[J]. 人民论坛·学术前沿, 2017(5):19-26.
WEN X. Space exploration is entering the era of spacecraft cluster [J]. Frontiers, 2017(5):19-26 (in Chinese).
[2] 牛禄, 王宏伟, 杨威. 用于微小卫星推进装置的脉冲等离子体推力器[J]. 上海航天, 2004, 21(5):39-43.
NIU L, WANG H W, YANG W. The pulsed plasma thruster for propeller in small and micro satellite [J]. Aerospace Shanghai, 2004, 21(5):39-43 (in Chinese).
[3] VENKATASUBRAMANIAN V, RENGASWAMY R, YIN K, et al. A review of process fault detection and diagnosis Part I: quantitative model-based methods[J]. Computers & Chemical Engineering, 2003, 27(3):293-311.
[4] VENKATASUBRAMANIAN V, RENGASWAMY R, KAVURI S N. A review of process fault detection and diagnosis Part II: quanlitative models and search strategies[J]. Computers & Chemical Engineering, 2003, 27(3):313-326.
[5] 贾庆贤, 张迎春, 李化义,等. 卫星姿态控制系统鲁棒故障诊断方法[J]. 哈尔滨工业大学学报, 2011, 43(3):19-22.
JIA Q X, ZHANG Y C, LI H Y,et al. LMI based robust fault diagnosis for satellite attitude control system[J].Journal of Harbin Institute of Technology, 2011, 43(3):19-22 (in Chinese) .
[6] 吴红芳, 王志. 基于扩展卡尔曼滤波器的航天器姿控飞轮故障诊断[J]. 航天控制, 2012, 30(3):34-37.
WU H F, WANG Z. The fault diagnosis of spacecraft attitude control flywheel based on extended Kalman filter[J]. Aerospace Control, 2012, 30(3):34-37 (in Chinese) .
[7] 吴丽娜, 张迎春, 赵石磊,等. 滑模观测器在卫星姿控系统故障诊断中的应用[J]. 哈尔滨工业大学学报, 2011, 43(9):14-18.
WU L N, ZHANG Y C, ZHAO S L,et al. Sliding mode observer usesd in satellite attitude control system fault diagnosis[J]. Journal of Harbin Institute of Technology, 2011, 43(9):14-18 (in Chinese) .
[8] 程瑶, 王日新, 徐敏强. 基于非线性未知输入观测器的航天器故障诊断[J]. 深空探测学报, 2015(3):278-282.
CHENG Y, WANG R X, XU M Q. Spacecraft actuator fault diagnosis based on nonlinear unknown input observer[J]. Journal of Deep Space Exploration, 2015(3):278-282 (in Chinese).
[9] WEN X,ZHANG X W,ZHU Y P. Design of fault detection observer based on hyper basis function[J]. Tsinghua Science and Technology,2015,20(2):200-2005.
[10] MOUSAVI S, KHORASANI K. Fault detection of reac-tion wheels in attitude control subsystem of formation flying satellites:a dynamic neural network-based approach[J].International Journal of Intelligent Unmanned Systems,2014,2(1):2-26.
[11] 王嘉轶, 闻新, 张婉怡. 卫星群反作用飞轮的故障诊断方法研究[J]. 中国空间科学技术, 2016, 36(4):24-32.
WANG J Y, WEN X, ZHANG W Y. Fault diagnosis of reaction wheel in satellite formation [J].Chinese Space Science and Technology, 2016,36(4):24-32 (in Chinese).
[12] 邓健. 脉冲等离子体推进器脉冲电源及推进剂烧蚀特性的实验研究和数值分析[D]. 南京:南京理工大学, 2013:4-6.
DENG J. Experimental research and numerical analysis of pulsed plasma thruster power supply and the ablative characteristics of characteristics propellant [D]. Nanjing: Nanjing University of Science and Technology, 2013:4-6 (in Chinese) .
[13] GUMAN W J, NATHANSON D M. Pulsed plasma microthruster propulsion system for synchronous orbit satellite[J]. Journal of Spacecraft & Rockets, 2012, 7(7):409.
[14] >LAPERRIERE D D. Electromechanical modelling and open-loop control of parallel-plate pulsed plasma microthrusters with applied magnetic fields[D]. Worcester:Worchester Polytechnic Institute, 2005:51-52.
[15] ASTON G, PLESS L C. Ignitor plug operation in a pulsed plasma thruster[J]. Journal of Spacecraft & Rockets, 2015, 19(3):250-256.
[16] NIETO P J G, GARCIA-GONZALO E, FERNNDEZ J R A, et al. A hybrid wavelet kernel SVM-based method using artificial bee colony algorithm for predicting the cyanotoxin content from experimental cyanobacteria concentrations in the Trasona reservoir (Northern Spain)[J]. Journal of Computational & Applied Mathematics, 2016, 309:587-602.
[17] WU Q. The forecasting model based on wavelet ν-support vector machine[J]. Expert Systems with Applications, 2009, 36(4):7604-7610.
[18] WEI C C. Wavelet kernel support vector machines forecasting techniques:case study on water-level predictions during typhoons[J]. Expert Systems with Applications, 2012, 39(5):5189-5199.
[19] ZHANG L, ZHOU W, JIAO L. Wavelet support vector machine[J]. IEEE Transactions on Systems Man & Cybernetics Part B Cybernetics A Publication of the IEEE Systems Man & Cybernetics Society, 2004, 34(1):34.
[20] DAUBECHIES I. The wavelet transform, time-frequency localization and signal analysis[J]. Journal of Renewable & Sustainable Energy, 2015, 36(5):961-1005.
[21] ZHANG Q, BENVENISTE A. Wavelet networks[J]. IEEE Transactions on Neural Networks, 1992, 3(6):889-898.
[22] 颜晓娟, 龚仁喜, 张千锋. 优化遗传算法寻优的SVM在短期风速预测中的应用[J]. 电力系统保护与控制, 2016, 44(9):38-42.
YAN X J,GONG R X, ZHANG Q F. Application of optimization SVM based on improved genetic algorithm in short-term wind speed prediction[J]. Power System Protection & Control, 2016, 44(9):38-42 (in Chinese).
[23] CHEN R, LIANG C Y, HONG W C, et al. Forecasting holiday daily tourist flow based on seasonal support vector regression with adaptive genetic algorithm[J]. Applied Soft Computing, 2015, 26(C):435-443.
[24] JUERGEN S. Electromechanical modeling and open-loop control of parallel-plate pulsed plasma microthrusters with applied magnetic fields[D]. Worcester:Worcester Polytechnic Institute, 2005:51-55.

