基于Gauss-Newton和UKF结合的微小卫星姿态确定算法

，，，

1. 南京航空航天大学 微小卫星研究中心，南京 210016 2. 上海卫星工程研究所，上海 201109

微小卫星姿态确定的精度取决于姿态敏感器的精度及姿态确定算法的精度[1]，微小卫星由于成本、体积、质量及功耗的限制，无法像传统大卫星一样自由选择姿态敏感器[2]，可以考虑采用微型器件，如微机电系统、光纤器件等，这些器件的性能指标低于传统器件，需要研究合适的姿态确定算法提升姿态确定精度。

目前微小卫星姿态确定的方法有两类，确定性算法和状态估计法[3]。确定性算法主要是求解Wahba问题[4]进行矢量定姿，典型的有TRIAD[5]、QUEST[6]、SVD[7]、FORM[8]、Eualr-q[9]等；对于求解误差能量函数最小问题，在数字信号处理领域广泛应用的还有“最陡梯度下降法”、Newton法[10]和Gauss-Newton(GN)算法，最陡梯度下降法能保证计算收敛，但收敛速度较慢；Newton法收敛速度较快，但计算复杂，需计算损失函数的二阶微分Hessian矩阵；Gauss-Newton算法仅计算一阶微分Jacobian矩阵，减小了计算量，而且保证计算收敛。确定性算法结构简单，设计容易，缺点是无法抑制观测噪声对姿态确定精度的影响[3]。

状态估计法采用非线性滤波方法实现最优姿态估计，应用最广泛的是扩展卡尔曼滤波(Extended Kalman Filter，EKF)[11]，但EKF只保留了Taylor的一阶近似项，不可避免引入线性化误差，如果线性化假设不成立，会导致滤波器的性能下降甚至造成滤波发散[12]。UKF滤波[13]基于UT变换对非线性函数的概率密度分布进行近似，未将高阶项忽略，对于非线性滤波有较高的计算精度，能有效解决EKF估计精度低、稳定性差的问题[14]。文献[15]利用地磁矢量作为测量信息，针对某LEO通信卫星仿真对比了EKF和UKF算法的估计精度、收敛时间和运算量，指出UKF在收敛速度、估计精度及跟踪姿态的快速变化等方面都优于EKF；而UKF的计算量大约为EKF的2n+1倍。

本文基于磁强计/太阳敏感器/陀螺的轻型低成本姿态敏感器配置，将确定性算法中的Gauss-Newton算法和状态估计法中的UKF滤波有机结合，提出一种组合算法，既克服了测量误差对姿态确定精度的影响，又减小了计算量。

1 卫星姿态描述

1.1 卫星姿态运动学方程

设q为轨道坐标系到星体坐标系的四元数，则由四元数来描述星体系相对于轨道系的姿态，得到卫星姿态运动学方程如下：

(1)

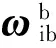
1.2 卫星姿态动力学方程

不含挠性部件的微小卫星可视为刚体，其相对惯性系的动力学方程为：

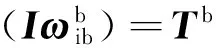
式中：I为卫星的惯量矩阵；Tb为作用于卫星的总力矩：

(4)

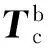
2 基于磁强计/太阳敏感器/陀螺 的姿态确定算法设计

2.1 姿态确定方案设计

确定性算法直接根据姿态敏感器的测量值确定姿态，算法简单，计算量小，但很难克服测量误差对姿态确定精度的影响[16]；而状态估计法能克服测量误差的影响，提供统计意义上的最优解，其中UKF滤波的精度和稳定性都要优于常用的EKF，但缺点是计算量较大[15]。

因此，本文基于“磁强计+太阳敏感器+陀螺”的轻型低成本姿态敏感器配置，将确定性算法中的Gauss-Newton和状态估计法中的UKF滤波有机结合，提出一种组合算法，如图1所示，先用Gauss-Newton初步解算，将磁强计和太阳敏感器的6维观测量转换为最优四元数qm，降低观测维数，并将观测方程转换成了线性方程，显著减少计算量，然后以最优四元数qm联合陀螺数据作为观测量，以姿态四元数和惯性系下的角速度作为状态量进行UKF滤波，以降低测量误差的影响，进一步提高姿态解算的精度。

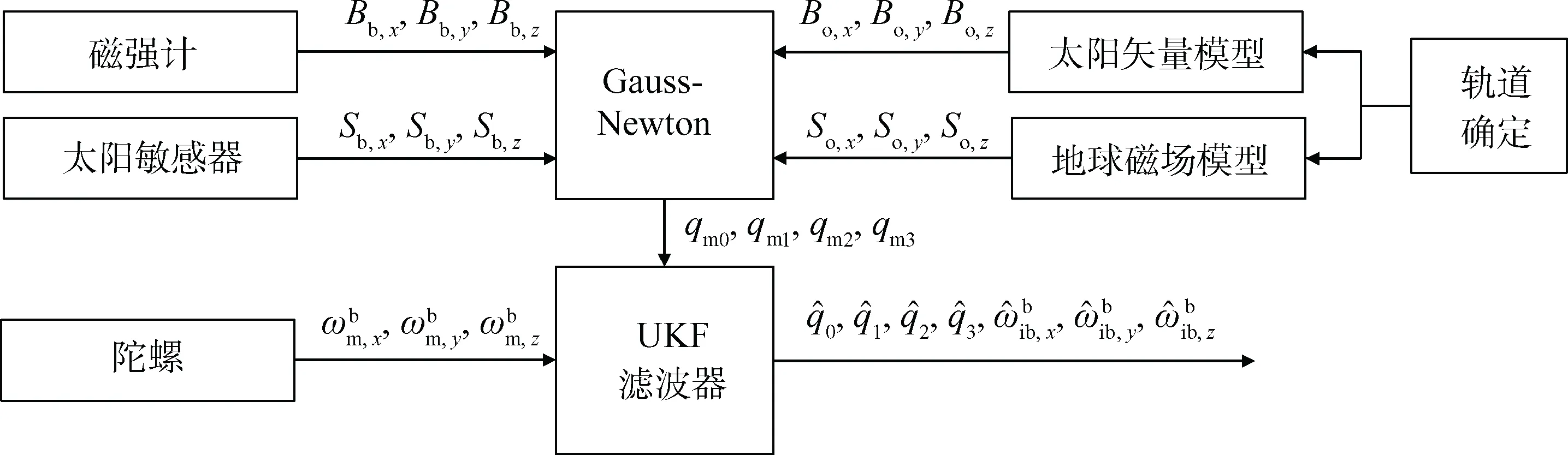
图1 姿态确定方案Fig.1 Attitude determination scheme

2.2 Gauss-Newton算法初步解算

矢量观测是姿态确定的主要方法，矢量观测就是利用姿态敏感器对当前时刻某些矢量(如恒星矢量、太阳矢量、地磁矢量等)的观测来计算卫星相对某参考坐标系的姿态，矢量观测方程可描述为：

AVi=Ui(i=1,2,…,n)(5)

式中：Vi为星体系中的观测矢量；Ui为参考坐标系中的参考矢量；A为星体系到参考系的姿态转换矩阵。确定性算法就是如何根据一组矢量观测值求出星体的姿态矩阵A。

当姿态敏感器选择为磁强计和太阳敏感器时，观测矢量有两对，即n=2。V1为磁强计测得的星体系下的地磁矢量观测值Bb，U1为根据卫星轨道参数和地球磁场模型计算得到的轨道系下的地磁矢量参考值Bo，V2为太阳敏感器测得的星体系下的太阳矢量观测值Sb，U2为根据卫星轨道参数和太阳矢量模型计算得到的轨道系下的太阳矢量参考值So。

Wahba将矢量观测描述为最小二乘估计问题，给出了一个求解姿态矩阵的、包含所有矢量测量信息的最小二乘性能指标，即能量损失函数[4]：

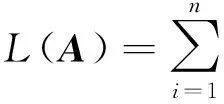
σi[Ui-AVi]T[Ui-AVi] =

式中：σi为各组矢量对的权系数；εi(q)为第i组测量与参考矢量之间的误差。最小化能量损失函数L(A)，即可求得加权最小二乘意义下姿态矩阵A的最优解。根据Gauss-Newton收敛算法，使得能量损失函数最小的四元数为[17]：

qk+1=qk-[J(qk)TJ(qk)]-1J(qk)Tε(qk)(7)

式中：J为Jacobian矩阵，定义为:

(8)

式(7)中的ε(qk)为观测矢量与参考矢量之间的误差：

式(7)中的J为如式(8)定义的Jacobian矩阵，具体为：

(10)

式中：yo,yb,M分别为：

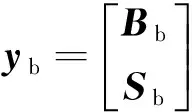
式中：A为用四元数描述的星体系到轨道系的姿态转换矩阵

则根据式(7)进行迭代计算即可求得最优四元数qm。其中由于姿态四元数的4个变量不独立，存在约束条件‖q‖=1，所以在整个姿态确定算法的过程中，都要进行四元数范数运算以保证四元数正规化。

2.3 滤波状态方程

(13)

2.4 滤波观测方程

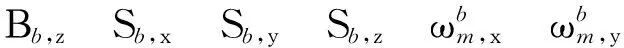
(14)

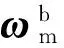
Z=I7×7X+V

(15)

2.5 UKF滤波

(1)步骤1

UT变换，获得一组Sigma点集。设非线性系统离散化后的模型为：

(16)

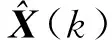
计算2n+1个Sigma采样点，这里的n指的是状态量的维数：

(17)

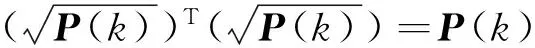
计算这些采样点相应的权值：

(18)

式中：ωm为计算均值时的采样点权值；ωc为计算协方差时的采样点权值，上标表示第几个采样点。

如此便通过UT变换获得了一组采样点(称为Sigma点集)及其相应权值：

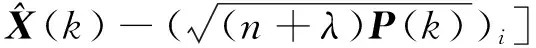
(2)步骤2

将Sigma点集带入式(13)的系统非线性状态方程计算Sigma点集的一步预测值。

(3)步骤3

计算系统状态量的一步预测及协方差阵，由Sigma点集的一步预测值加权求和计算系统状态量的一步预测及协方差阵:

(20)

P(k+1|k)=

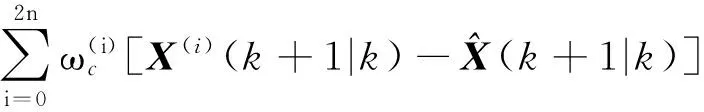
(4)步骤4

根据一步预测值，再次使用式(17)进行UT变换，产生新的Sigma点集：

X(i)(k+1|k)=

(5)步骤5

将新的Sigma点集带入线性观测方程式(15)，得到系统预测的均值和协方差。

(6)步骤6

预测观测量均值和协方差，由观测量预测值加权求和得到：

·

根据式(23)～(25)，由观测量预测值加权求和计算系统预测均值及协方差。

(7)步骤7

由式(26)计算卡尔曼增益矩阵，由式(27)(28)计算系统的状态更新和协方差更新：

(26)

(27)

P(k+1)=P(k+1|k)-K(k+1)PZk,ZkKT(k+1)

(28)

3 仿真结果与分析

仿真参数设定如下：

1)磁强计测量误差300nT(3σ)，太阳敏感器测量误差1.5°(3σ)。

2)陀螺常值漂移0.001(°)/s，测量白噪声0.01(°)/s，随机漂移白噪声0.002(°)/s。

4)轨道高度600 km，轨道倾角97.4°，轨道角速度0.001 083 rad/s。

6)仿真时间5 000 s，仿真步长0.1 s。

分别仿真Gauss-Newton(GN)、直接UKF滤波(UKF)、Gauss-Newton与UKF滤波组合(GN+UKF)这3种算法，仿真结果如图2～5所示。

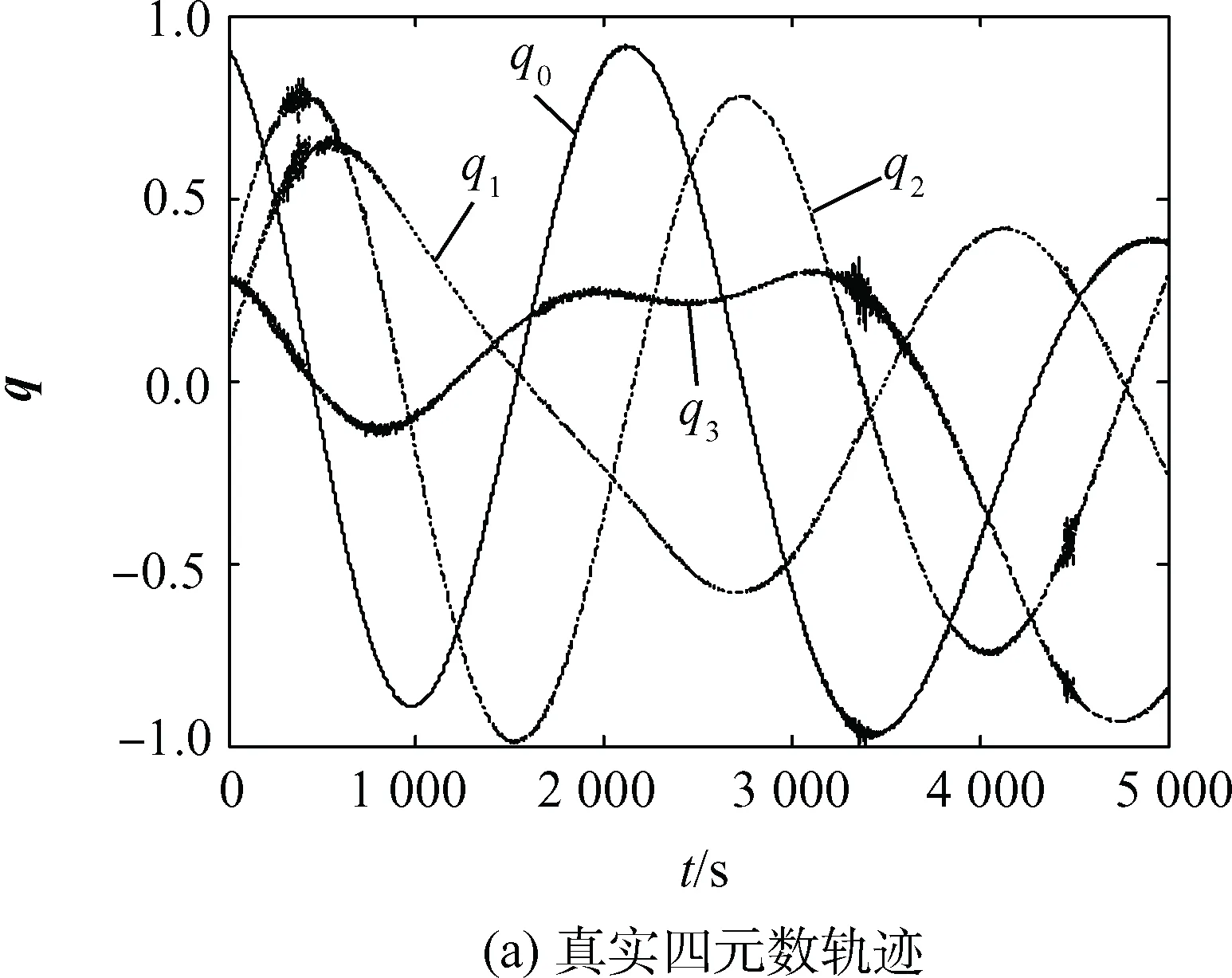
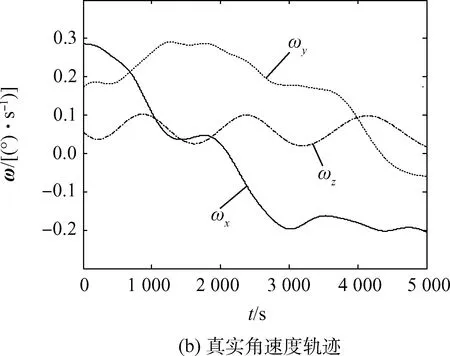
图2 姿态运动真实轨迹Fig.2 True trajectory of attitude motion

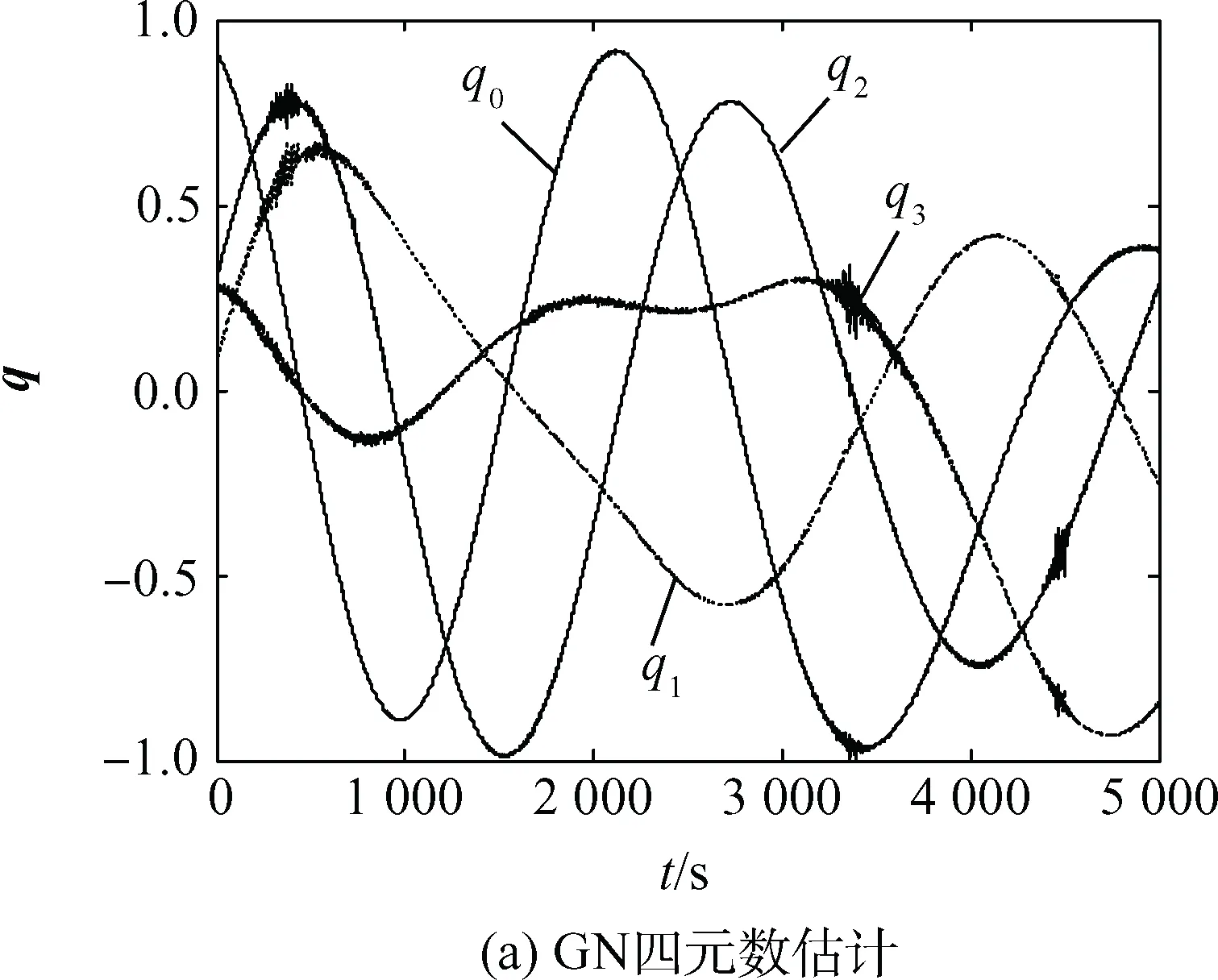
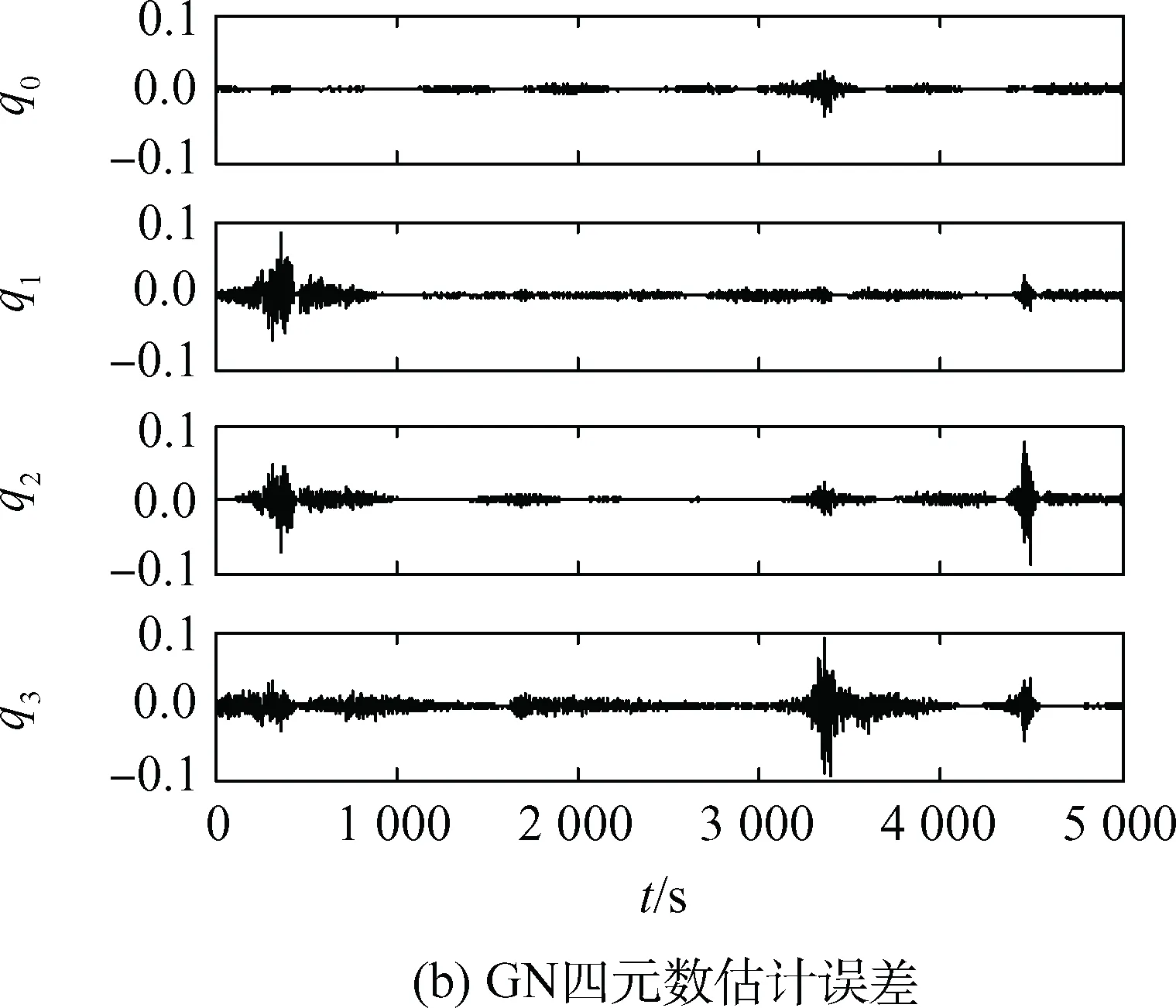
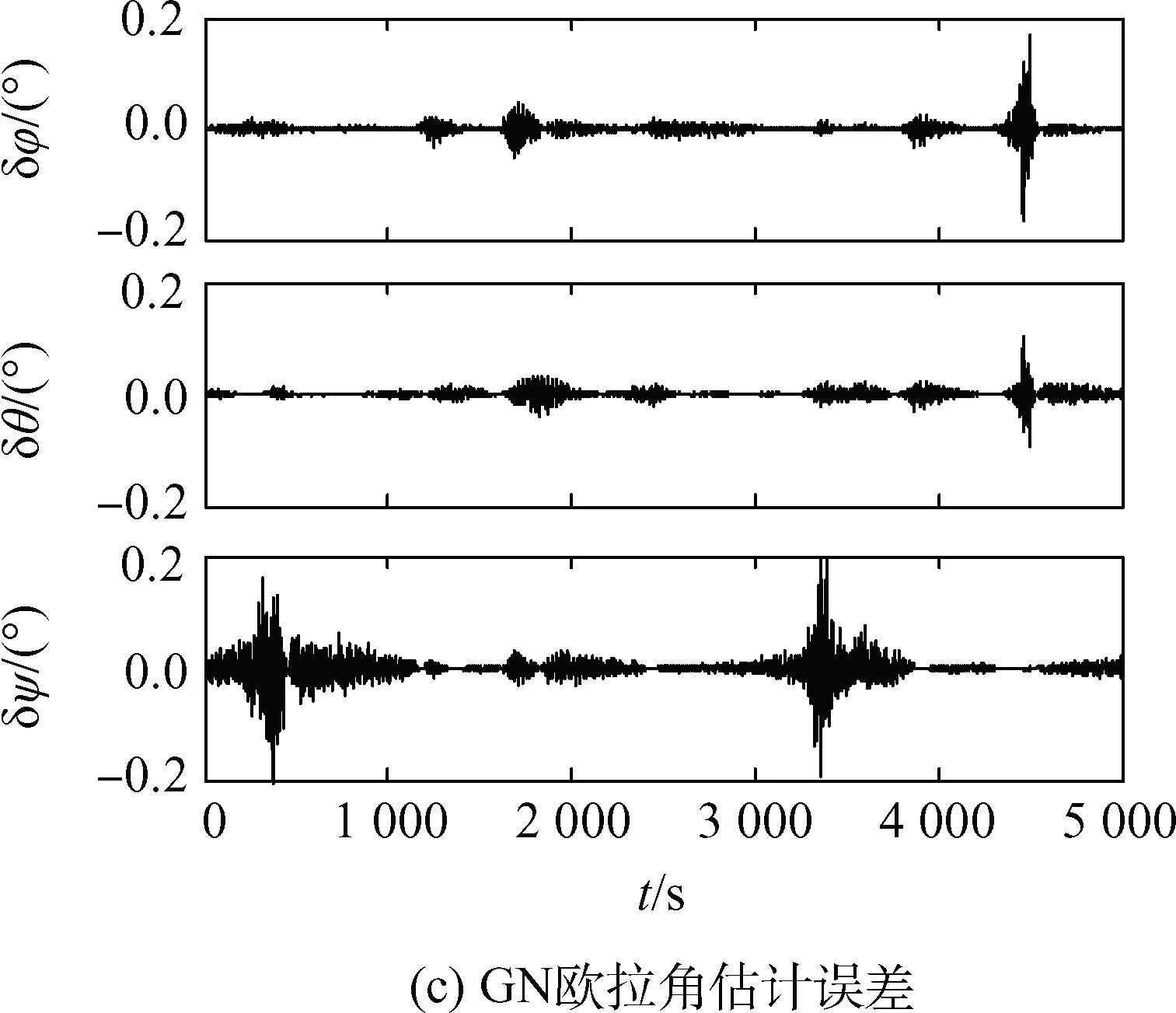
图3 GN姿态确定结果Fig.3 Attitude determination results of GN

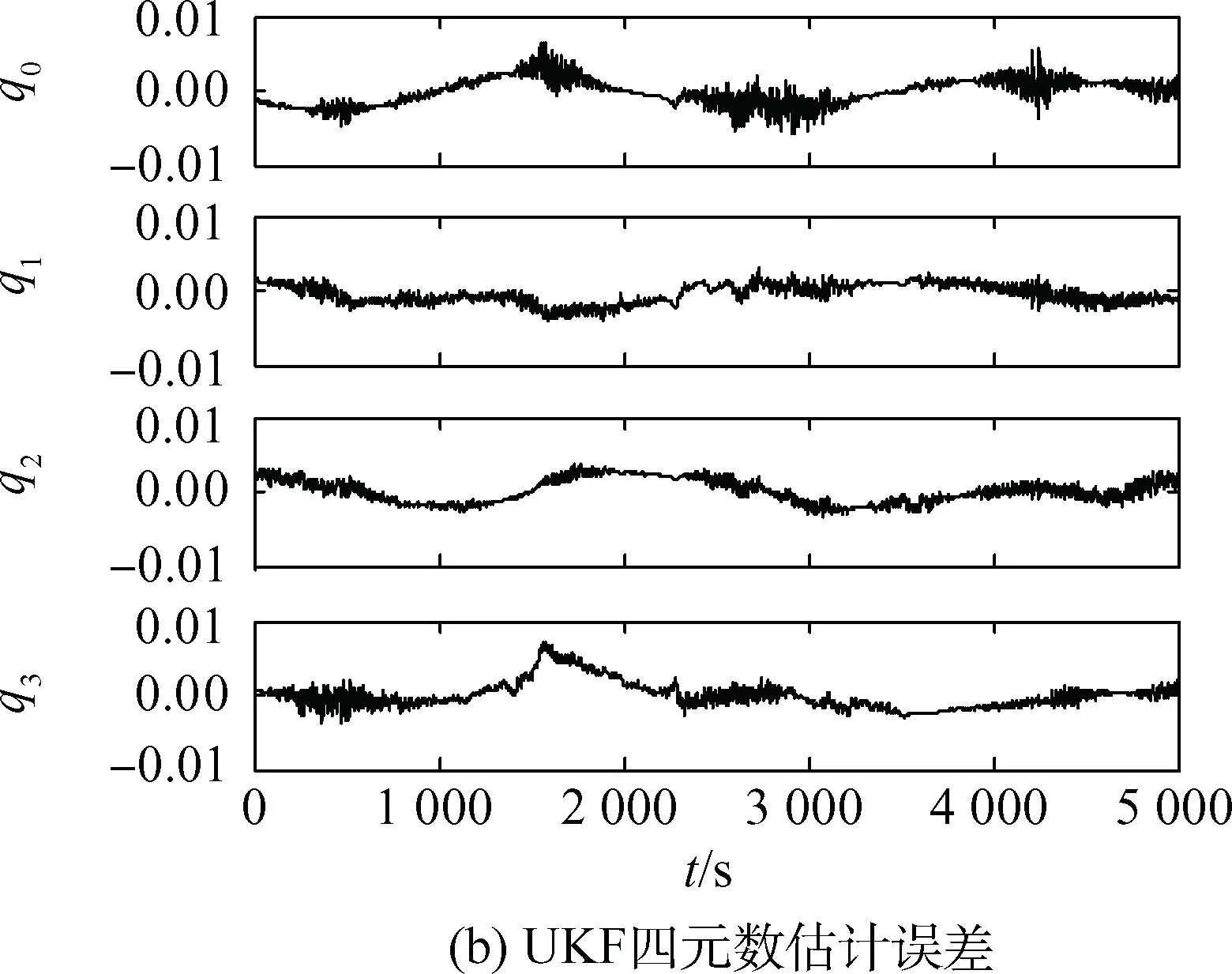
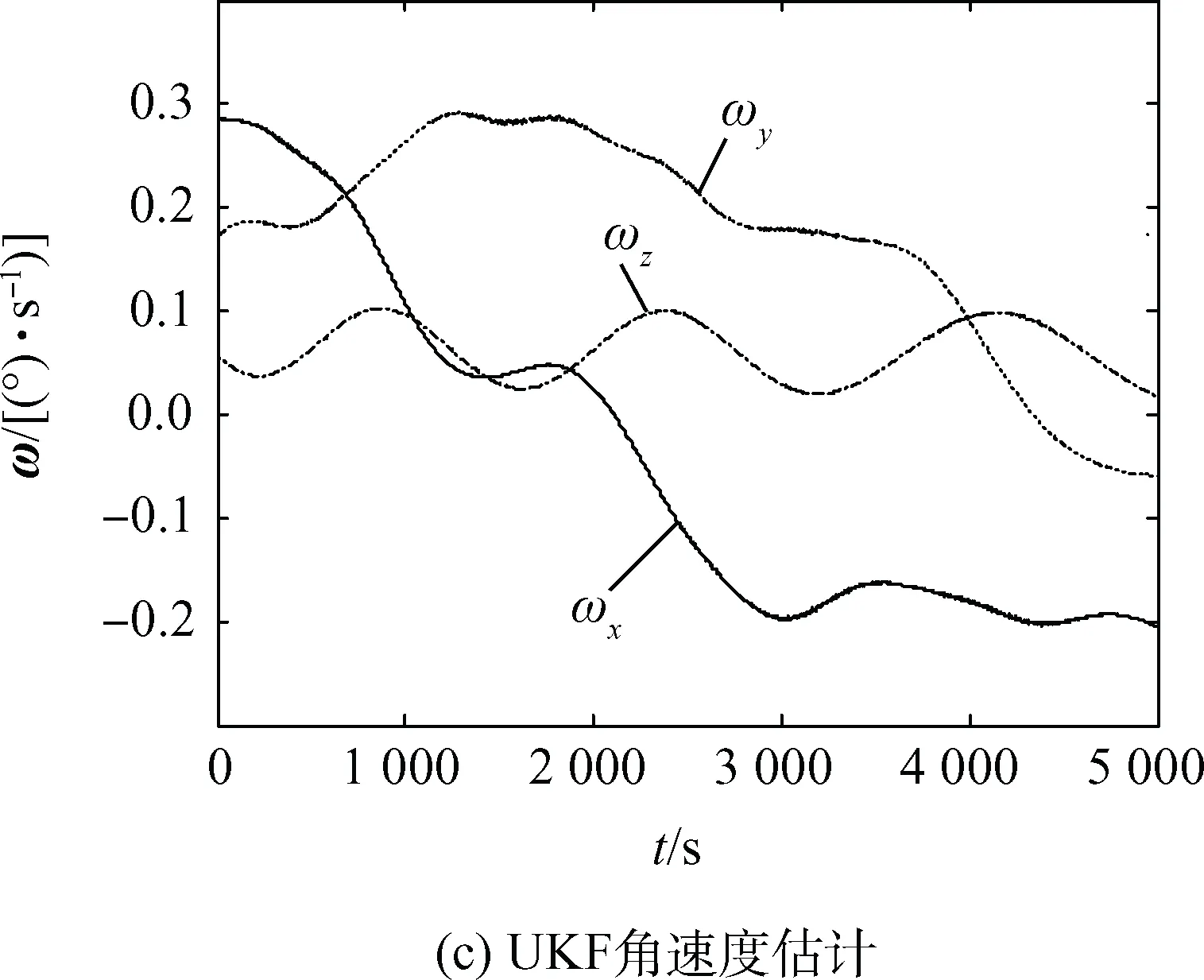
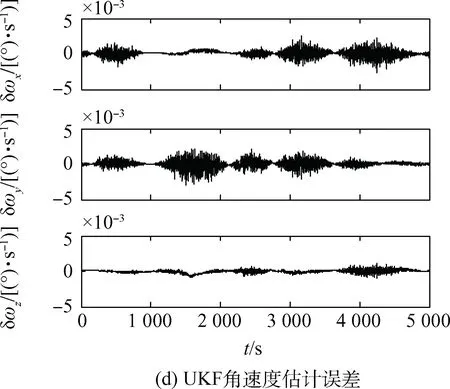
图4 UKF姿态确定结果Fig.4 Attitude determination results of UKF

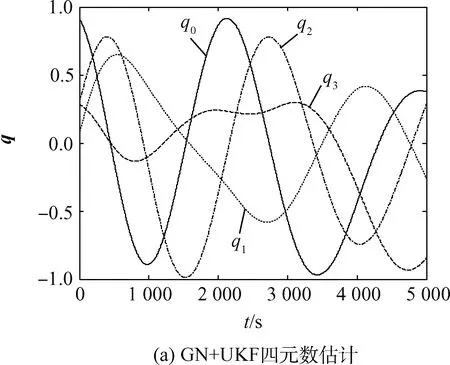
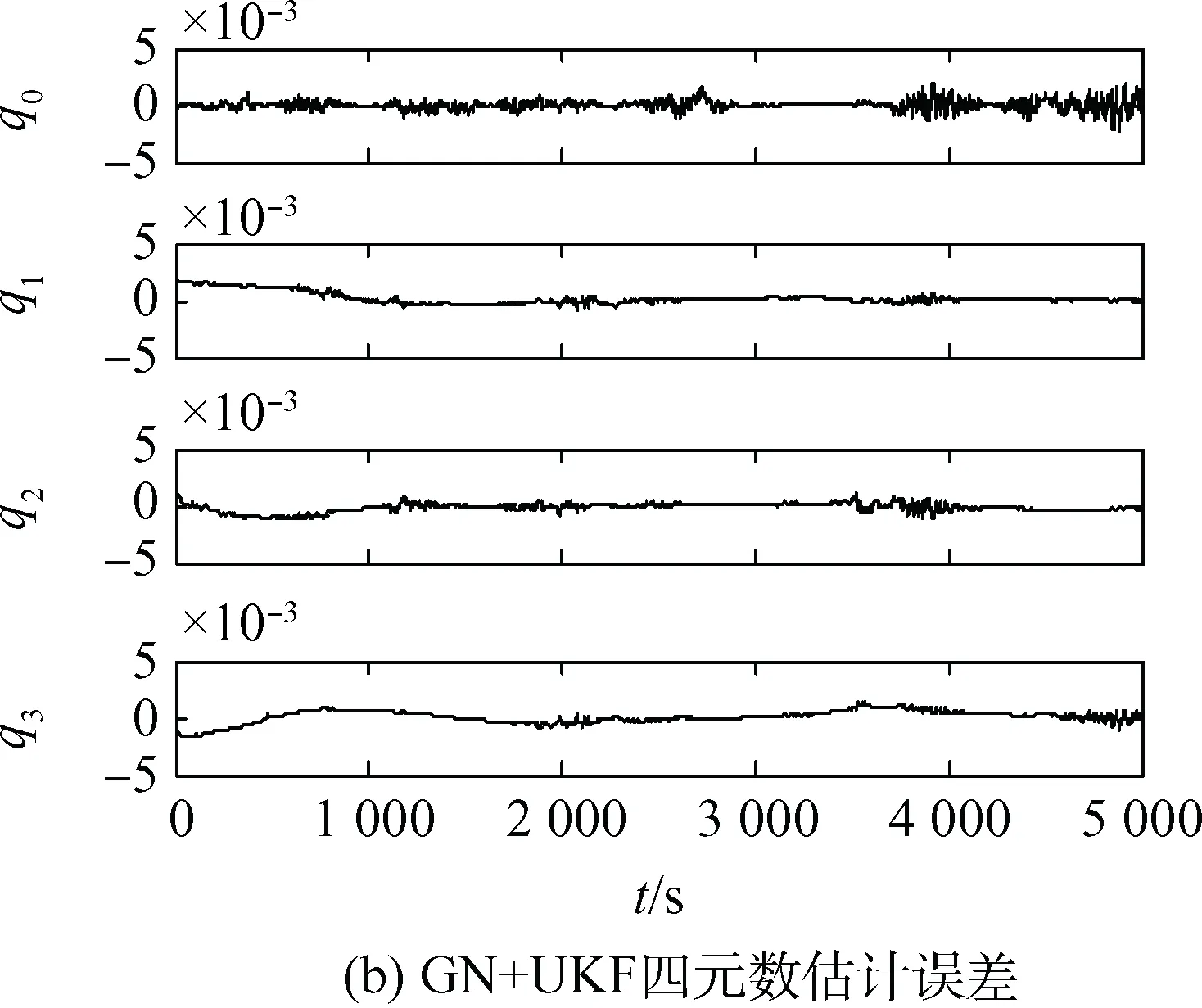
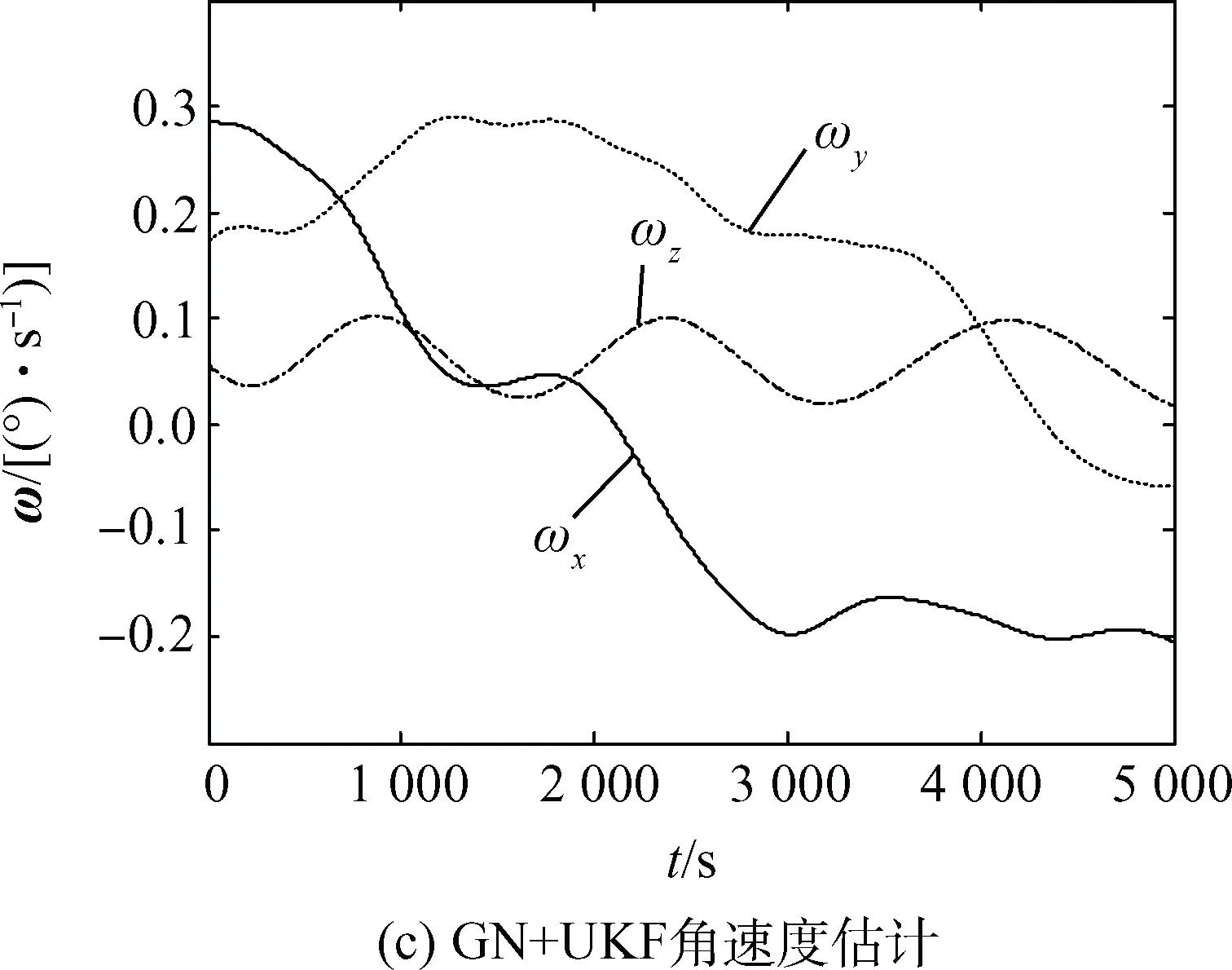
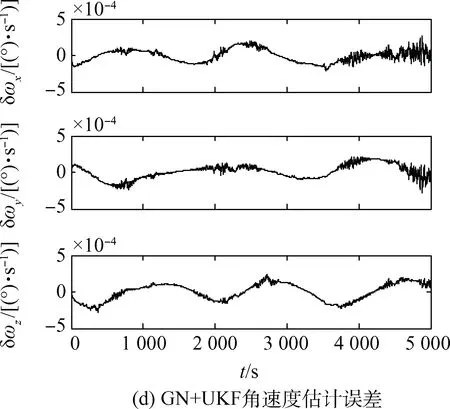
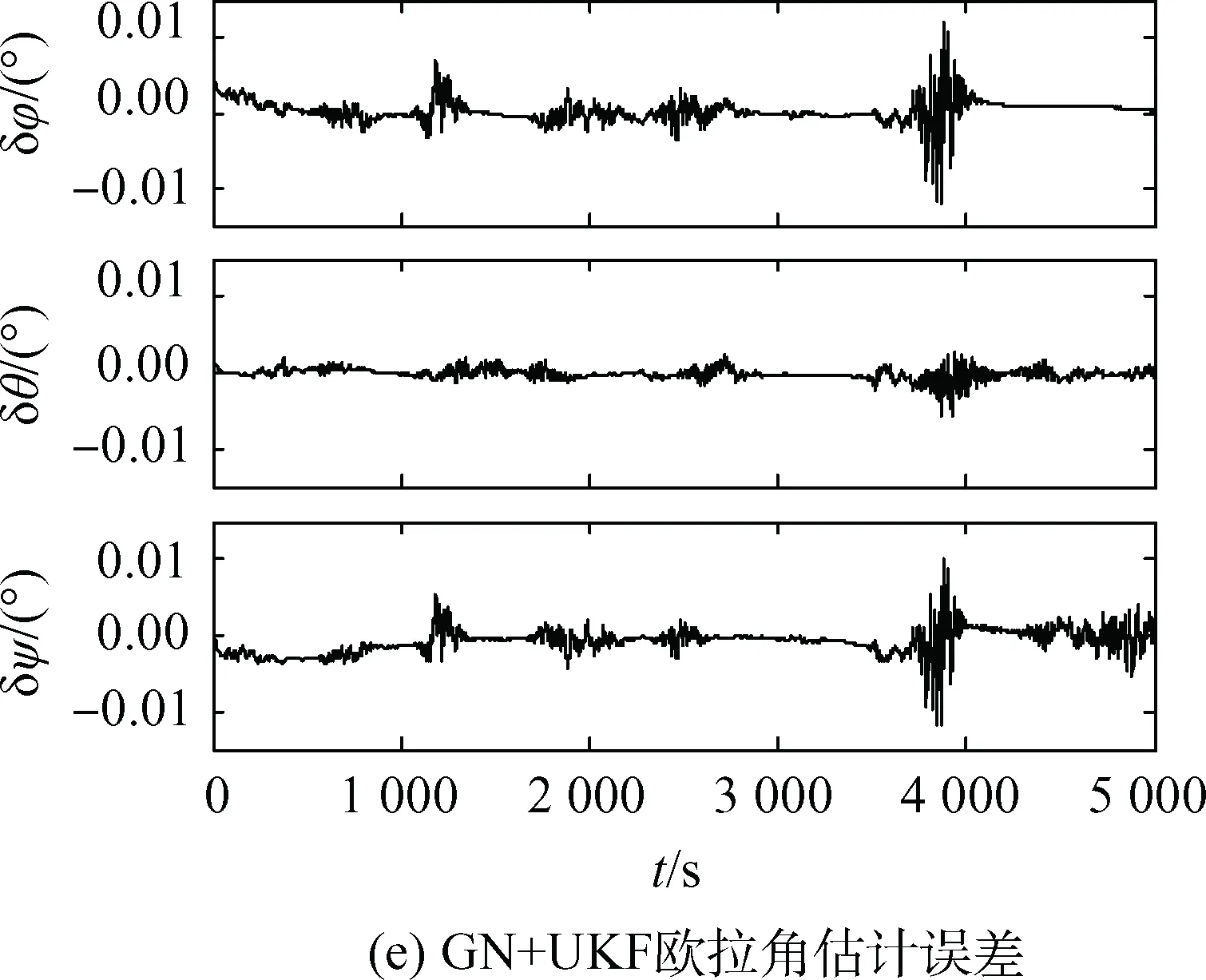
图5 GN+UKF姿态确定结果Fig.5 Attitude determination results of GN+UKF

GN、UKF、GN+UKF算法的三轴角度和角速度估计误差如表1所示。

表1 三种算法估计误差对比

由图3(c)、图4(e)、图5(e)对比GN、UKF、GN+UKF算法的三轴角度估计误差，GN的三轴角度估计误差在0.2°以内，UKF的三轴角度估计误差在0.02°以内，精度相比GN提升了10倍，而GN+UKF算法的三轴角度估计误差在0.01°以内，相比UKF提升了2倍，相比GN提升了20倍。

由图4(d)、图5(d)对比UKF、GN+UKF的三轴角速度估计误差，UKF的三轴角速度估计误差在0.005(°)/s以内，而GN+UKF的三轴角速度估计误差在0.000 5(°)/s以内，相比UKF提升了10倍。

由此说明，先用Gauss-Newton初步解算，再进行UKF滤波的组合算法比单独使用这两种方法精度都要高，而且由于将观测量从9维降阶为7维，并将观测方程转化为线性方程，相比直接UKF还减小了计算量。

4 结束语

本文基于磁强计/太阳敏感器/陀螺的微型低成本姿态敏感器配置，设计了Gauss-Newton迭代算法和UKF滤波相结合的微小卫星姿态确定算法，既减少了计算量，又提高了姿态确定精度，为微小卫星提供了一种低成本高精度的姿态确定方案。

参考文献(References)

[1] 张晨. 基于星跟踪器的航天器姿态确定方法研究[D]. 武汉：华中科技大学，2005：10-11.

ZHANG C. Research on spacecraft attitude determination method based on star tracker[D]. Wuhan: Huazhong University of Science and Technology，2005：10-11(in Chinese).

[2] 邢艳军，王永富，陆亚东. 微小卫星鲁棒自适应姿态确定算法[J]. 中国空间科学技术，2015，35(1)：27-35.

XING Y J，WANG Y F，LU Y D. Robust adaptive attitude determination algorithm for micro satellite [J]. Chinese Space Science and Technology，2015，35(1)：27-35(in Chinese).

[3] 王新国，李爱华，许化龙. SUKF在导弹姿态估计中的应用[J]. 系统工程与电子技术，2009，31(1)：170-173.

WANG X G，LI A H，XU H L. Application of SUKF in missile attitude estimation[J]. Systems Engineering and Electronics，2009，31(1)：170-173(in Chinese).

[4] WAHBA G. A least-square estimate of spacecraft attitude[J]. SLAM Rev.，1965，409(7)：12.

[5] SHUSTER M D，OH S D. Three-axis attitude determination from vector observations[J]. Journal of Guidance，Control，and Dynamics，1981，4(1)：70-77.

[6] CHOUKROUN D，BAR-ITZHACK I Y， OSHMAN Y. Optimal-request algorithm for attitude determination[J]. Journal of Guidance，Control，and Dynamics，2004，27(3)：418-425.

[7] MARKLEY F L. Attitude determination using vector observations and the singular value decomposition[J]. Journal of the Astronautical Sciences，1987，38(3)：245-258.

[8] MARKLEY F L. Attitude determination from vector observations: a fast optimal matrix algorithm[J]. Journal of the Astronautical Sciences，1993，41(2)：261-280.

[9] MORTARI D. Euler-q algorithm for attitude determination from vector observations[J]. Journal of Guidance Control & Dynamics，1998，21(2)：328-334.

[10] 刘海颖. 微小卫星姿态控制系统关键技术研究[D]. 南京：南京航空航天大学，2008：34-35.

LIU H Y. Research on key technologies of micro-satellite attitude control system[D]. Nanjing: Nanjing University of Aeronautics and Astronautics，2008：34-35(in Chinese).

[11] LEFFERTS E J，MARKLEY F L，SHUSTER M D. Kalman filtering for spacecraft attitude estimation[J]. Journal of Guidance Control & Dynamics，1982，5(4)：536-542.

[12] 李鹏，唐健，段广仁，等. 基于自适应联邦滤波的卫星姿态确定[J]. 中国空间科学技术，2013，33(2)：67-71.

LI P，TANG J，DUAN G R，et al. Satellite attitude determination based on adaptive federal filter[J]. Chinese Space Science and Technology，2013，33(2)：67-71(in Chinese).

[13] JULIER S J，UHLMANN J K. New extension of the Kalman filter to nonlinear systems[J]. Proceedings of SPIE-The International Society for Optical Engineering，1999，3068：182-193.

[14] 徐成刚. 基于非线性预测滤波和UKF的状态估计方法[J]. 科技信息，2013(19)：174-176.

XU C G. A state estimation method based on nonlinear predictive filtering and UKF[J]. Science and Technology Information，2013(19)：174-176(in Chinese).

[15] 杨斌，徐广涵，靳瑾，等. 磁定姿近地轨道卫星EKF与UKF算法比较[J]. 中国空间科学技术，2012，32(6)：23-30.

YANG B，XU G H，JIN J，et al. Comparisons of EKF and UKF algorithms for near-earth orbit satellites[J]. Chinese Space Science and Technology，2012，32(6)：23-30(in Chinese).

[16] MARINS J L，YUN X P，BACHMANN E R，et al. An extended Kalman filter for quaternion-based orientation estimation using MARG sensors[C]. Proceedings of the 2001 IEEE/RSJ International Conference on Intelligent Robots and Systems，Hawaii，USA，2001：2003-2011.

[17] 谢祥华. 微小卫星姿态控制系统研究[D]. 南京：南京航空航天大学，2007：4-5.

XIE X H. Research on microsatellite attitude control system[D]. Nanjing: Nanjing University of Aeronautics and Astronautics，2007：4-5(in Chinese).