满足多终端约束的二次曲线迭代制导方法研究
,,
北京航天自动控制研究所,北京 100854
迭代制导技术早在美国“阿波罗计划”中的“土星-V”火箭的制导方案中已经使用。之后,美国的航天飞机,法国的“阿里安”火箭和俄罗斯的“能源号”火箭也都采用了迭代制导技术,并取得了良好的效果[1-3]。在中国载人火箭上使用的迭代制导方法已经经过多次载人任务的考核,成熟可靠,适应能力强,并且将该方法尝试在月面上升段使用,效果良好[4]。但上述使用的迭代制导方法是通过改变发动机推力矢量方向来修正轨道偏差,从而达到精确入轨的目的,由此带来的问题就是入轨时刻的姿态角必须由制导算法决定,而不能预先确定,否则最后时刻推力矢量的偏差将可能使迭代制导的精度优势荡然无存[5]。
国内外对迭代制导方法研究已开展多年[6-8],理论已经相当成熟。综合而言,迭代制导方法只能满足速度和位置约束,无法满足终端姿态约束,尤其对某些常推力火箭而言,传统的迭代方法无法同时满足3个速度和位置分量的终端约束[6]。
针对传统迭代制导法无法同时满足多终端约束的问题,尤其是终端姿态约束的难题,最为直接有效的方法就是在火箭入轨末端具备调姿系统,在不影响质心运动状态的情况下将姿态调整至要求值,可以同时确保轨道和姿态满足要求。而在不具备调姿系统的情况下,可以考虑在小推力发动机工作段结束前进行姿态调整的方法,提前估计需要调整的角度并进行补偿,降低调姿造成的速度偏差,通过初步的仿真表明,该方法能够起到一定的作用,但由于难以准确估计调整角度,效果并不十分理想[5]。
本文在传统迭代制导方程的基础上引入终端姿态约束方程,通过二次曲线形式的制导程序角进行计算与规划,推导出跨越主机段和游机段的全真空飞行段的迭代制导程序角计算方法,解决了同时满足高精度入轨和姿态约束问题,实现运载火箭的包括轨道根数和姿态等多个终端约束下的直接入轨,同时利用数学仿真对该方法进行深入细致仿真分析。
1 二次曲线迭代制导方法
1.1 基本原理
为了精确使用姿态、速度、位置等终端条件,将二次曲线迭代制导计算所用坐标系设为轨道坐标系O′-ξηζ,其定义原点在地心,O′η轴与预报入轨点的矢径方向重合;O′ξ轴在轨道平面内指向飞行方向;O′ζ轴与其他两轴构成右手坐标系,如图1所示。
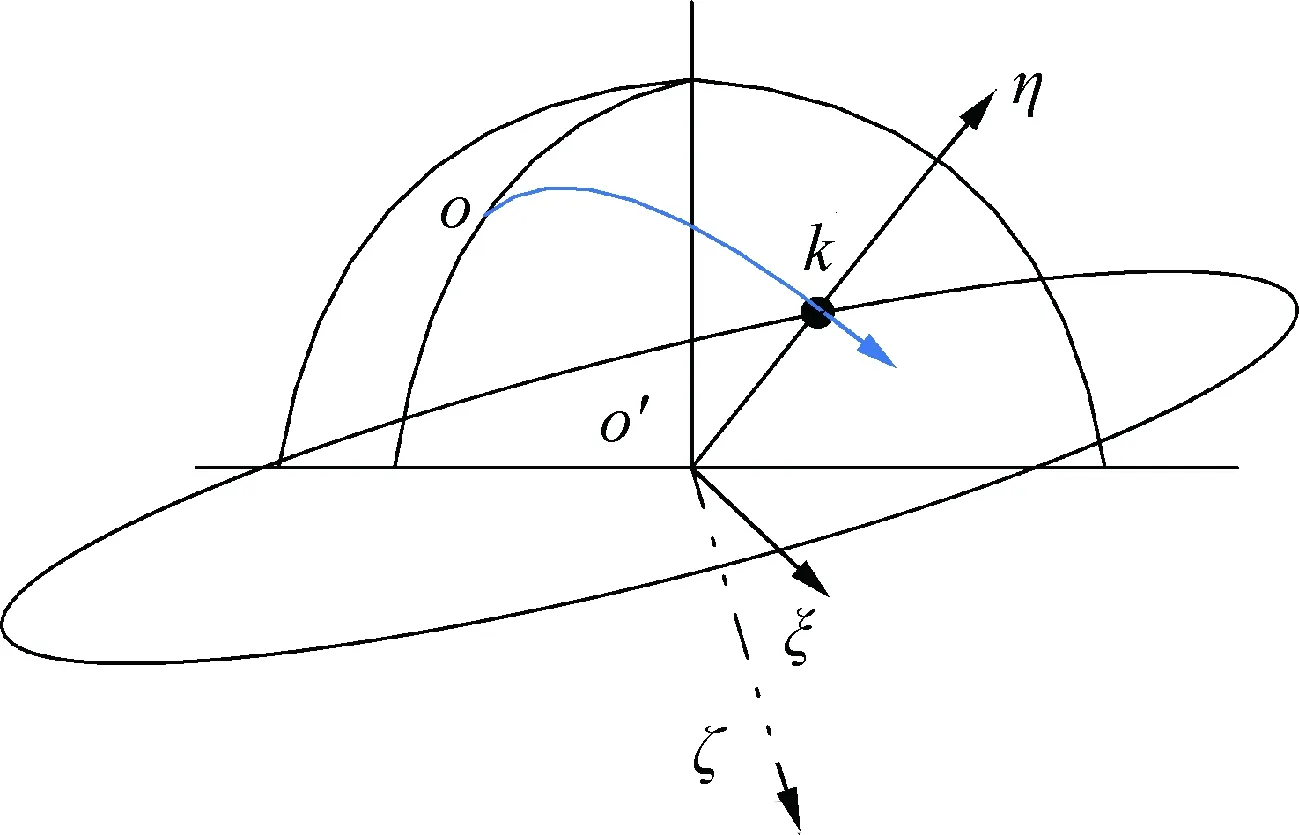
图1 轨道坐标系Fig.1 Orbital coordinate system
迭代制导是一种满足多终端指标约束条件的最优制导方法,具有抗干扰能力强、制导精度高、终端姿态有约束等优点。迭代制导的理论基础是最优控制。根据最优控制理论,以火箭当前状态(主要包括速度矢量和位置矢量)作为初值,以入轨点状态作为终端条件,以燃料消耗最少作为性能指标,将发动机推力矢量方向作为控制变量,根据Pontliyagin极小值原理可以实时计算出一条最优弹道[9]。
在轨道坐标系下展开的运动方程为:
(1)
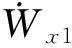
制导系统通过改变箭体纵轴方向实现对火箭质心运动的控制。传统迭代方法使用的制导控制程序角方程是线性形式[10],导致其用于调节的控制参数有4个,在满足位置与速度约束条件的前提下,无法再满足姿态约束。为同时满足多个终端约束,则将用于制导的程序角方程设为二次曲线形式,使其不但可满足速度与位置约束条件,还能满足姿态约束条件,具体程序角方程为:
(2)
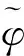
1.2 约束条件
制导程序角要满足多个约束条件,利用平均程序角保证平均速度约束,而(-k1+k3t+k5t2)和(-k2+k4t+k6t2)可以保证瞬时速度、位置和姿态约束,约束方程的建立可通过对运动方程的展开形式进行积分即可得到。由于运载火箭的整个真空飞行段会包括多个飞行段,比如大推力段和小推力段,则程序角需要在整个真空段满足上述约束条件。
1)假设只有终端速度约束,终端位置ζk,ηk,ξk可以任意,则由极小值原理的哈密顿方程得到制导方程的最优解:
(3)
式中:Vζ k,Vη k为入轨时刻轨道坐标系下的速度分量;Vζ0,Vη0为当前时刻轨道坐标系下的速度分量;Tk为剩余飞行时间。
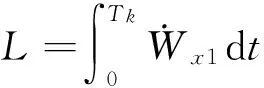
2)假设在条件1)的基础上,还需满足位置约束、姿态约束,则需要调节(-k1+k3t+k5t2)和(-k2+k4t+k6t2)中的系数k1~k6,满足上述约束条件。
针对上述公式,可得到如下几个约束方程求解程序角系数。
对偏航控制通道上进行约束方程的建立,如下所示。
偏航程序角:
(4)
偏航通道上的速度约束方程可通过对式(1)分别在真空飞行段进行积分得到:
ψ*+gζ)dt+
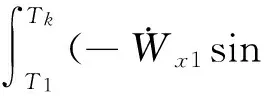
式中:T1为迭代接入时刻到主机关机这段时间,Tk-T1为游机段飞行时间。
偏航通道上的位置约束方程可通过对速度方程继续积分得到:
ζk-ζ0-Vζ0·tk=
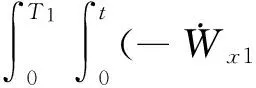
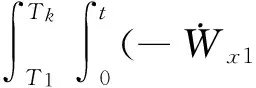
(6)
式中:ζk,ζ0分别为入轨时刻和当前时刻的在轨道坐标系的位置分量。
在俯仰控制通道上进行约束方程的建立,如下所示。
俯仰程序角:
(7)
俯仰通道上的速度约束方程可通过对式(1)分别在整个飞行段进行积分得到:
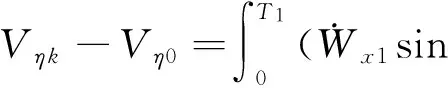
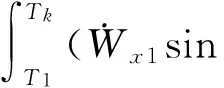
(8)
俯仰通道上的位置约束方程可通过对速度方程继续积分得到:
ηk-η0-Vη0tk=
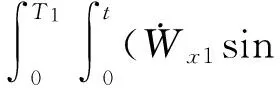
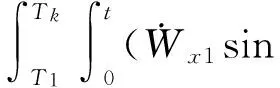
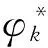
1.3 程序角的推导
对于运载火箭而言,要求程序角变化平滑,以利于姿态的平稳控制,故满足位置和姿态约束的调节量相对于总调节量而言应占很小的部分[4],因此可作小角度近似假设,即:
cos (-k1+k3t+k5t2)≈1
sin(-k1+k3t+k5t2)≈-k1+k3t+k5t2
因此,代入上述约束方程可得:
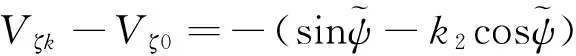
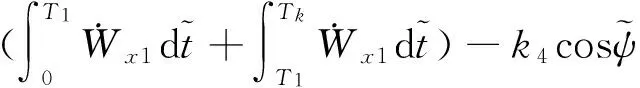
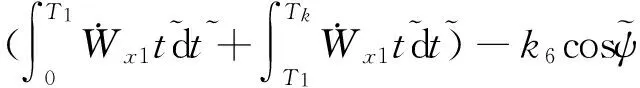
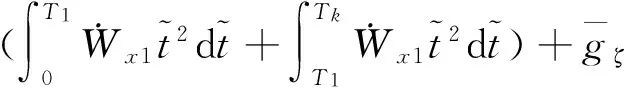
则偏航方向速度对应的方程可得到:
同理,可简化其他偏航通道的位置约束方程:
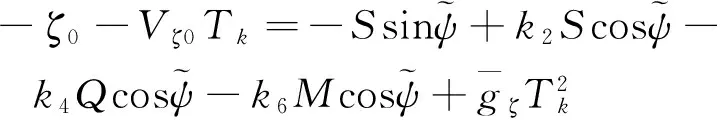
也可简化俯仰通道的速度和位置约束方程:令
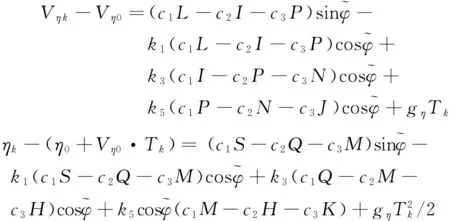
由上述公式可得到相应的程序角系数:
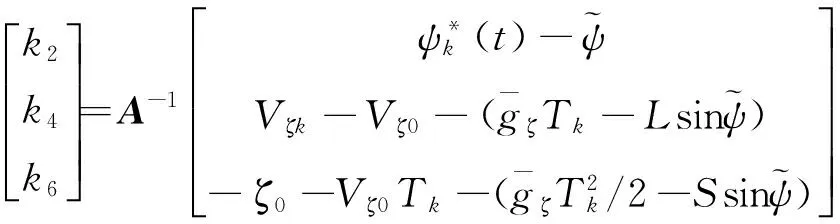
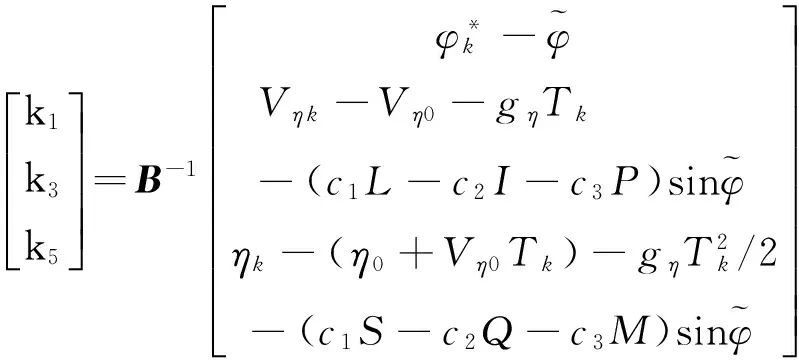
其中:
综上所述,通过式(10)、式(11)中6个约束方程的求解,可实时得到程序角系数k1~k6,从而就可实时得到制导程序角进行控制。因此,火箭在满足高精度入轨时,姿态也能满足终端约束。
1.4 剩余飞行时间的确定
主机段常用速度等关机量的相关方式进行关机,因此可以利用传统的计算速度增量的方法来确定主机段和游机段剩余飞行时间T1、T2,即可以根据速度增量进行剩余飞行时间的估计:
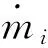
Tk=T1+T2
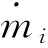
2 应用仿真分析
以某运载火箭为例进行六自由度数学仿真,对二次曲线迭代制导性能及姿态约束能力加以验证。仿真目标轨道为近地圆轨道。标准状态下迭代制导阶段轴向过载曲线见参考文献[7]。仿真设置在350 s开始接入迭代制导,直至飞行器所带载荷进入目标轨道。
2.1 无干扰状态下入轨性能及姿态约束能力
不加入任何干扰的状态下,数学仿真结果显示,传统迭代制导及二次曲线迭代制导方法使得火箭具有如表1所示的入轨精度。

表1 无干扰状态迭代制导入轨精度
表1中,ΔT为轨道周期偏差,ΔHp为轨道近地点高度偏差,Δi为轨道倾角偏差,ΔΩ为轨道升交点经度偏差。
由表1可知,二次曲线迭代制导与传统的迭代制导的入轨精度基本相当,但二次曲线迭代制导对姿态角进行了约束,如图2所示。
图2 无干扰状态迭代制导程序角Fig.2 Programangle of IGM in non-disturbance state
图2中Fcx表示标准飞行程序角,Fai表示二次曲线迭代制导计算的飞行程序角。图2反映了二次曲线迭代制导与标准弹道的程序角差别。其中迭代制导接入处(350 s)的角度变化约为2°,而传统迭代制导变化约为0.8°[5],其原因是二次曲线迭代制导方法为了满足终端姿态约束,通过二次曲线形式来规划要满足多个约束条件的制导程序飞行姿态角。
2.2 偏差状态下入轨性能及姿态约束能力分析
为了验证偏差状态下二次曲线迭代制导方法的入轨性能及姿态约束能力,对大的结构偏差(负偏差)情况进行了仿真计算,结果如表2所示。
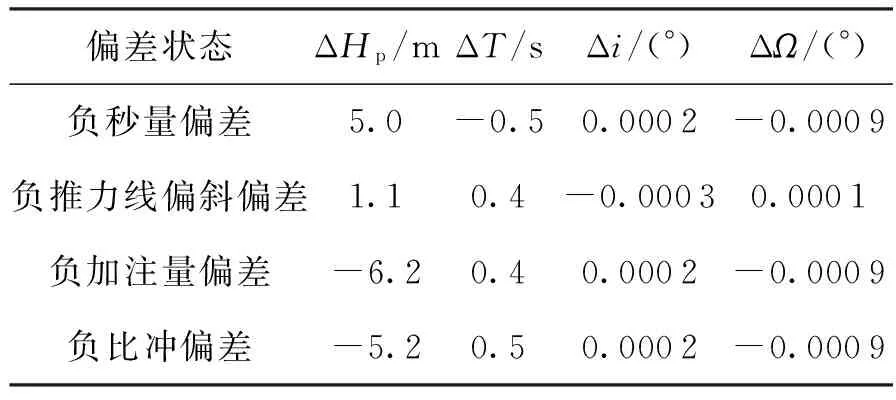
表2 不同偏差状态的入轨性能统计对比
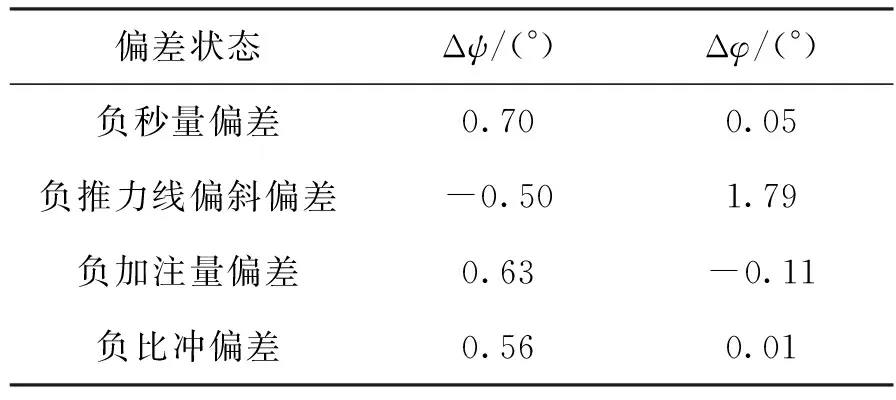
表3 不同偏差状态的姿态约束能力
表3中Δφ为入轨时刻与约束入轨角的偏航角偏差,Δψ为入轨时刻与约束入轨角的俯仰角偏差。
将二次曲线迭代制导与传统迭代制导、摄动制导方法在所有发动机处于负秒流量偏差状态下,对入轨性能进行对比分析,分析结果如表4所示。

表4 所有发动机的秒流量负偏差状态下的入轨性能
结果表明,二次曲线迭代制导的入轨性能不亚于传统迭代制导方法,且其入轨性能远远高于摄动制导方法。尤其直接考核入轨性能的指标,如近地点高度、轨道倾角和升交点经度,二次曲线迭代制导方法相对于摄动制导方法而言都具有不可比拟的优势。
选取对飞行姿态角较为敏感的发动机推力线偏斜偏差状态进行仿真计算,其迭代制导程序角曲线如图3所示。
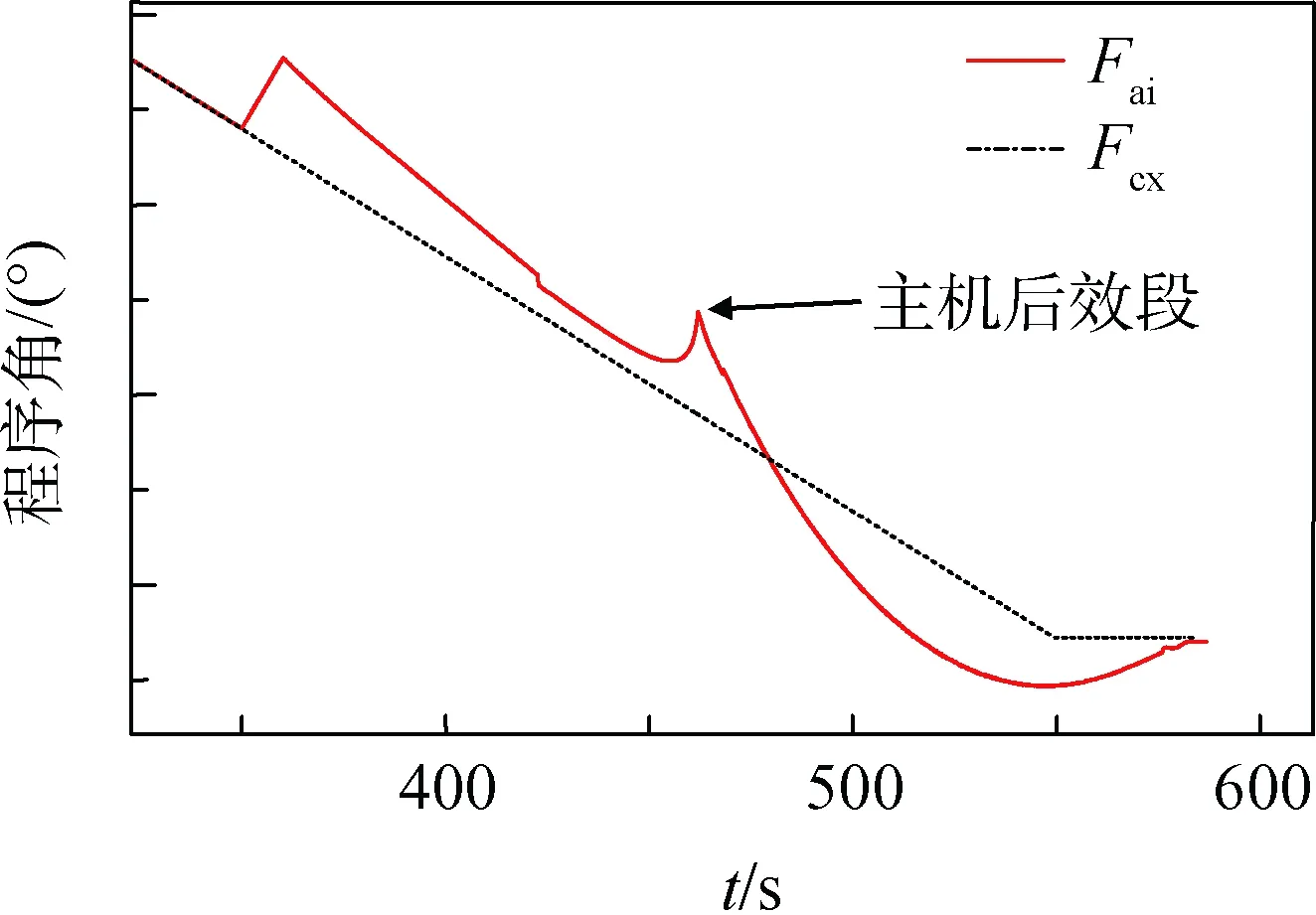
图3 发动机负推力线偏斜状态的迭代制导程序角Fig.3 Program angle of IGM in negativethrust line skew deviation
由图3可知,在主机段与游机段的整个真空飞行段,迭代制导程序角呈现了二次曲线特征,终端姿态也实现了约束的姿态角入轨。在主机段切换到游机段的主机后效段,由于推力过载发生了变化,引起剩余飞行时间预估值产生变化,使得飞行程序角产生了比较大的跳变。
综上所述,二次曲线迭代制导在入轨精度上不亚于传统迭代制导的精度指标,且其入轨姿态也实现了终端姿态角约束要求。
2.3 约束姿态角变化的入轨性能和姿态约束能力分析
为了全面考核二次曲线迭代制导的制导性能及终端姿态角约束能力,在不改变目标轨道根数的情况下,设置不同约束的俯仰姿态角,来分析其入轨性能与姿态约束能力。
传统火箭的俯仰姿态角相对于偏航姿态角要变化明显,因此设置约束俯仰姿态角分别为10°、-10°、-30°、-50°、-70°。偏航姿态角为0°。其数学仿真结果显示二次曲线迭代制导具有如表5~表7所示的入轨性能及姿态约束能力。
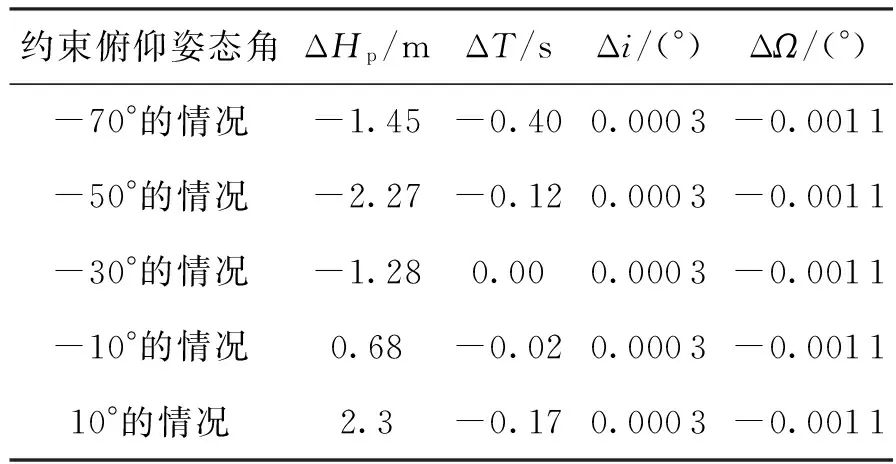
表5 无干扰情况下不同约束姿态角的入轨性能对比
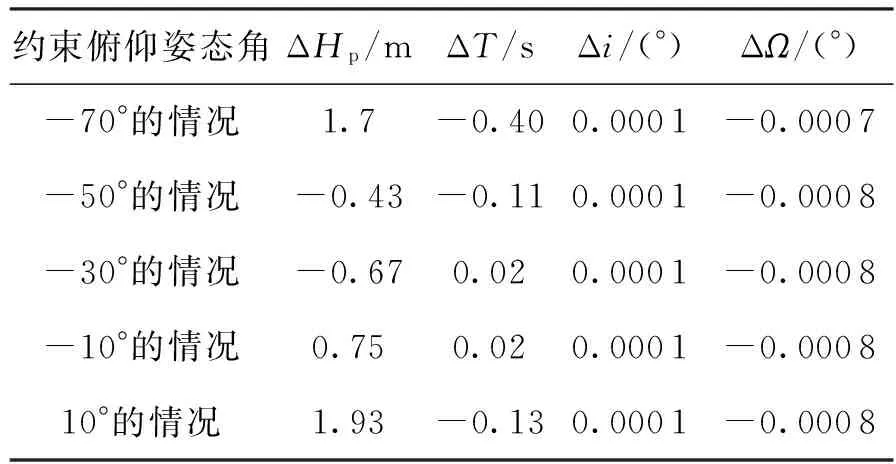
表6 负推力线偏斜偏差情况下不同约束姿态角入轨性能
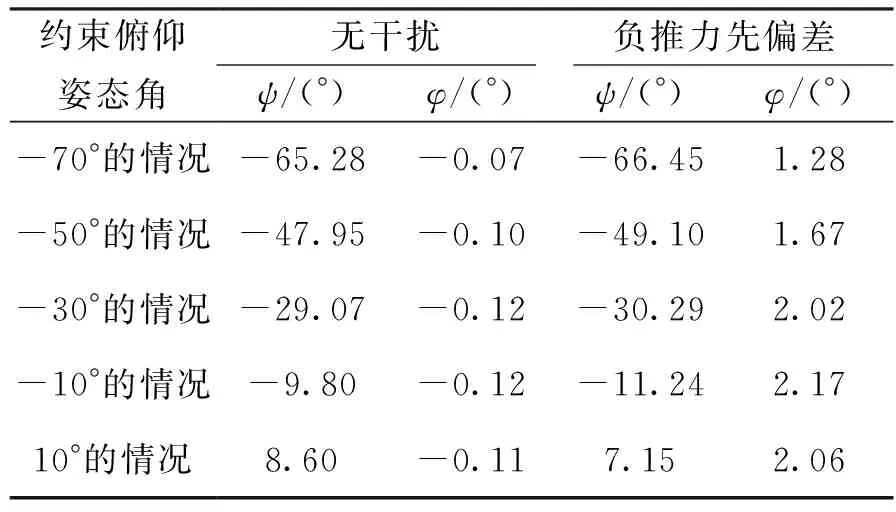
表7 不同姿态约束角的姿态约束能力对比
表7中φ为入轨时刻的偏航角,ψ为入轨时刻的俯仰角。
由表7可知,在无干扰及负推力线偏差状态下,姿态约束的迭代制导方法能满足不同姿态约束角变化的要求,图4、图5给出了各个约束姿态角下俯仰姿态角变化曲线。
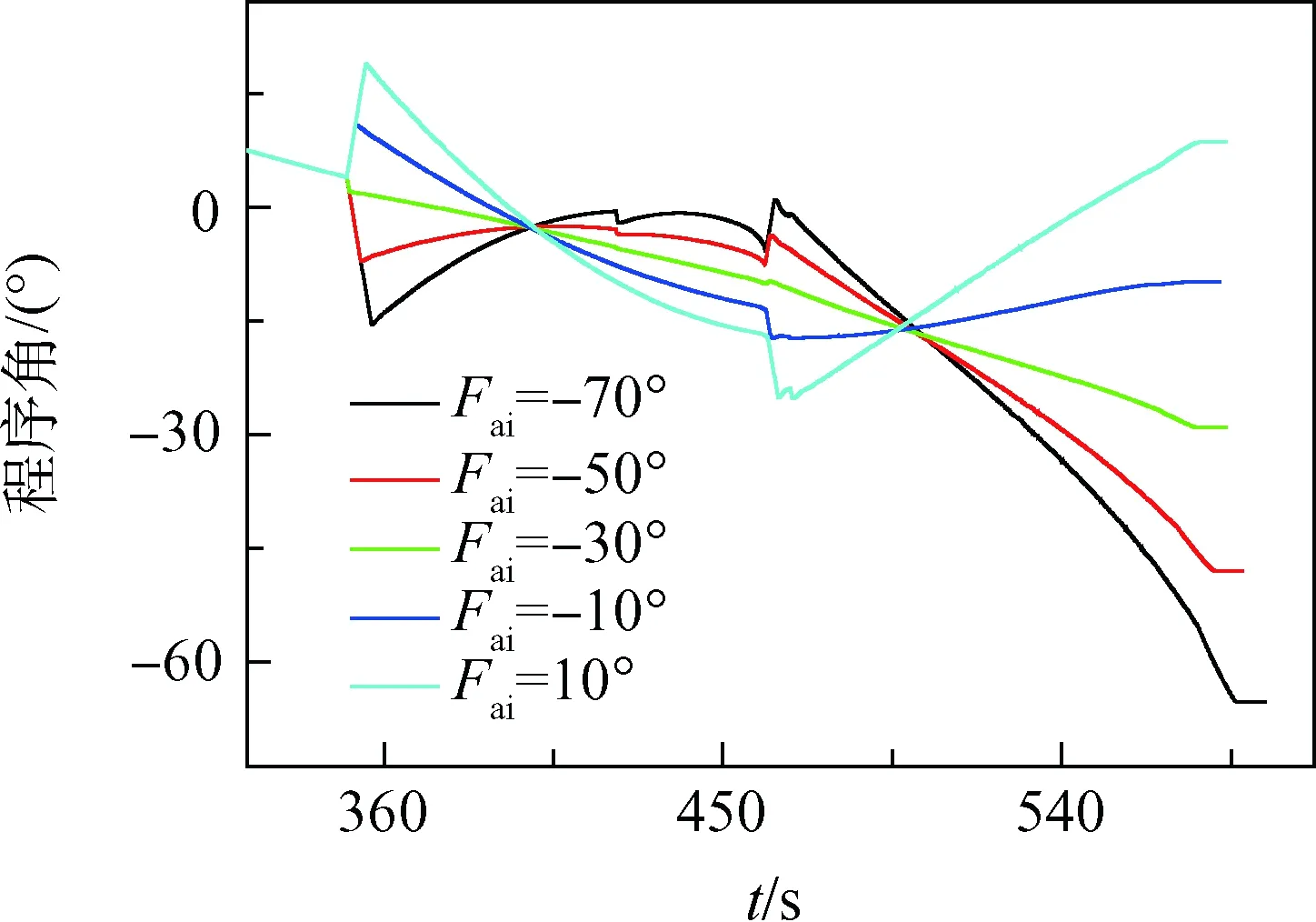
图4 无干扰状态Fig.4 Non-disturbancestate
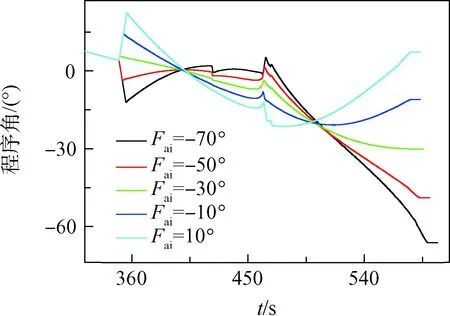
图5 负推力线偏差状态Fig.5 Negative thrust line skew deviation state
由图4、图5可知,本方法在不同的约束终端姿态角情况下,接入迭代时刻的程序角会跳变至不同的起始程序角,从而导致形成不同的抛物线姿态角曲线参与制导控制,最后均可按照约束姿态角实现火箭入轨。
2.4 轨道根数小幅变化下的入轨性能及姿态约束能力分析
满足多终端姿态约束迭代制导的特点是在飞行过程中计算一条能满足终端约束姿态角要求的飞行弹道。当轨道根数发生变化情况下,只要适时地调整迭代制导的目标轨道等数据,二次曲线迭代制导也能自己规划出一条弹道飞向改变后的轨道,这与传统迭代制导方法的思想是一致的。传统的迭代制导方法能适应轨道的小幅调整[2],因此,为了验证本方法的能力,也在轨道根数小幅变化的情况下进行了仿真分析,仿真偏差范围如表8所示。

表8 轨道参数变化
设定终端约束俯仰姿态角为-30°,约束的偏航姿态角为0°,姿态约束的迭代制导的入轨性能及姿态约束能力分析如表9、表10所示。
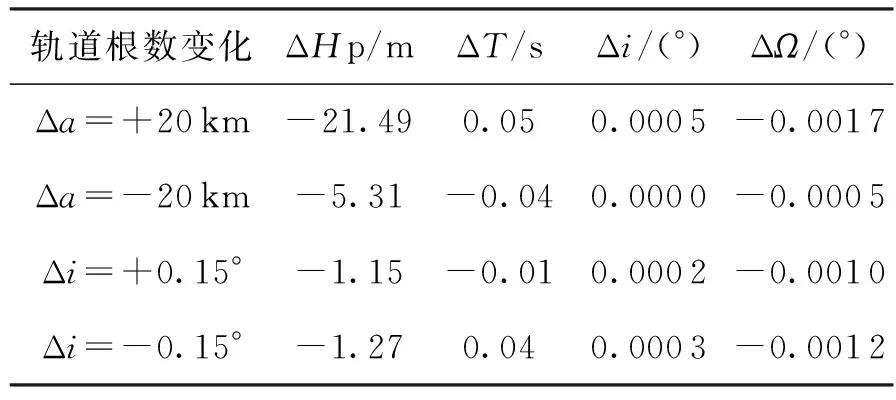
表9 轨道根数小幅变化状态下的入轨性能表
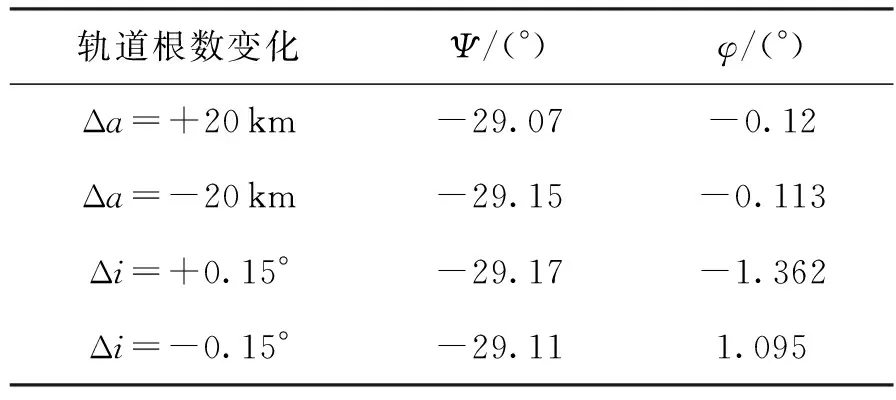
表10 轨道根数变化小幅变化状态下的姿态约束能力表
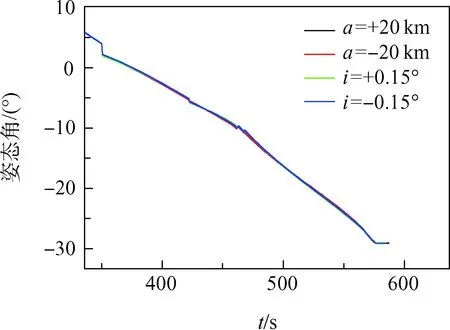
图6 俯仰姿态角曲线Fig.6 Pitch attitude angle curve
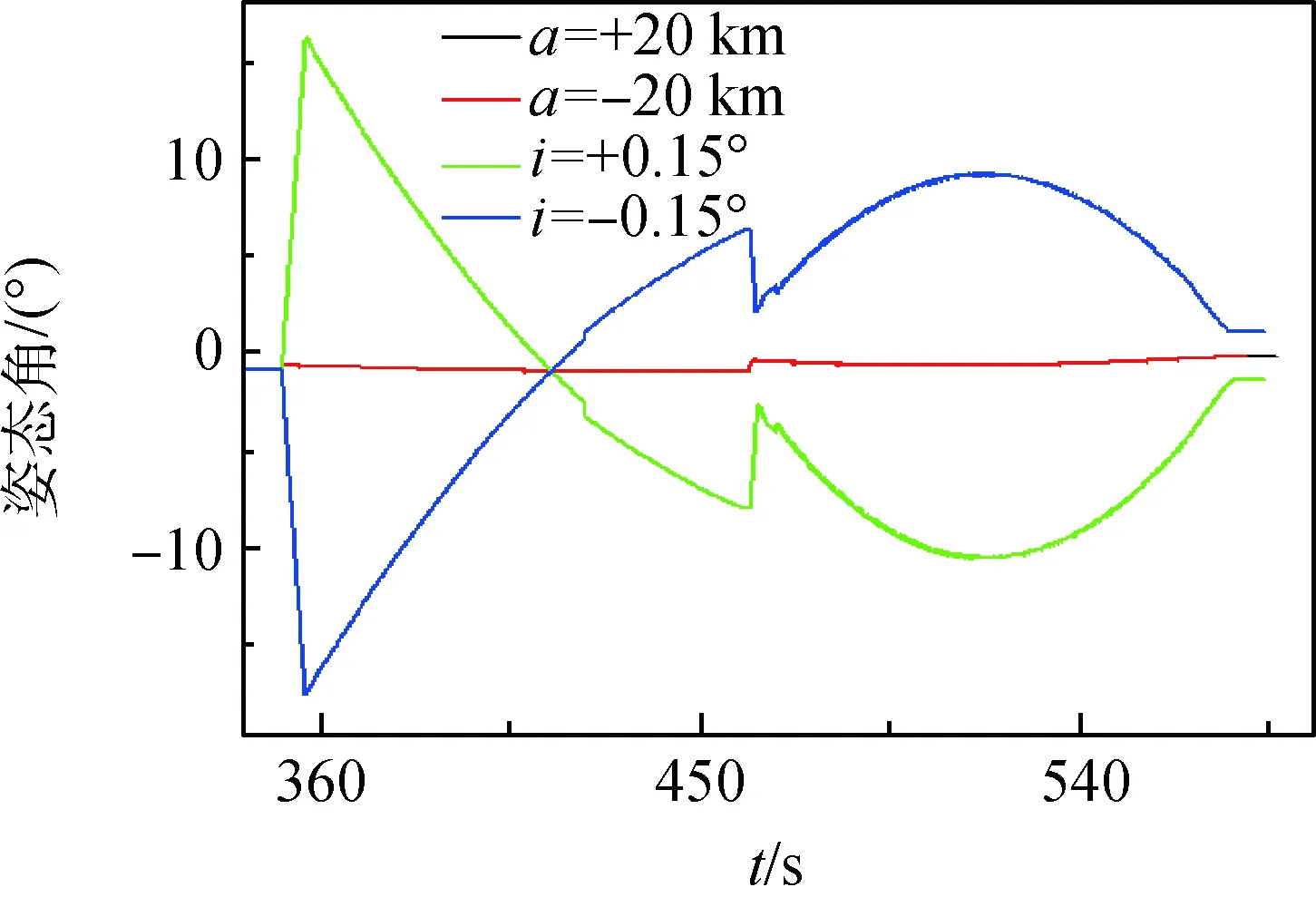
图7 偏航姿态角曲线Fig.7 Yaw attitude angle curve
图6与图7是半长轴与轨道倾角分别变化时的俯仰角、偏航角曲线,可以看到,为了适应对轨道倾角0.15°的变化,偏航通道具有了明显的程序角调整措施。而对于轨道半长轴的变化,对应的俯仰和偏航姿态角变化均很小。
可见,在轨道根数发生小幅变化时,姿态约束的迭代算法与传统迭代算法一样能保持稳定,入轨精度影响不大。
3 结束语
本文针对传统迭代制导无法约束入轨姿态的不足,提出了一种横跨整个真空飞行段的满足多个终端约束的迭代制导方法,该方法通过二次曲线规划制导程序角来实现对速度、位置和姿态进行约束。结果表明,本方法不仅保持传统迭代制导方法入轨精度的同时,而且还能满足高精度的入轨约束姿态角要求,并能在一定范围内适应约束姿态角与轨道根数的变化,可以满足后续发射任务需求,具有重要的工程应用价值。
参考文献(References)
[1] HAEUSSERMANN W. Description and performance of the Saturn launch vehicle′s navigation,guidance and control system,NASA-TND-5869[R]. Washington D.C.:National Aeronautics and Space Administration, 1970.
[2] MARTIN D T, SIEVERS R F. Saturn V guidance[J].J.Spacecraft,1967,4(7):891-898.
[3] TEOFILATTO P, PASQUALE E D. Adaptive guidance by a direct method[C]. 48th International Astronautical Congress,6-10 October,1997.
[4] 巩庆海,宋征宇,吕新广.迭代制导在月面上升段的应用研究[J].载人航天,2015,21(3):231-236.
GONG Q H,SONG Z Y,LYU X G.Study on application of iterative guidance in lunar ascent[J].Manned Spaceflight,2015,21(3):231-236(in Chinese).
[5] 吕新广,宋征宇. 载人运载火箭迭代制导方法应用研究[J].载人航天,2009(1).
LYU X G. SONG Z Y.Application of iterative guidance method for manned carrier rockets [J]. Journal of Spacecraft, 2009(1) (in Chinese) .
[6] 陈新民,余梦伦. 迭代制导在运载火箭上的应用研究[J].
宇航学报,2003,24(5):484-489.
CHEN X M, YU M L. Study of iterative guidance application to launch vehicles[J]. Journal of Astronautics,2003,24(5):484-489 (in Chinese).
[7] 茹家欣.液体运载火箭的一种迭代制导方法[J].中国科学(E辑:技术科学) ,2009,39(4):696-706.
RU J X. An iterative guidance method for liquid launch vehicle[J].Chinese Science (Series E: Technical Science), 2009, 39(4):696-706(in Chinese).
[8] 吴楠,程文科,王华.运载火箭迭代制导方法的改进研究[J].动力学与控制学报,2009,7(3):279-282.
WU N, CHENG W K, WANG H. Animproved iterative guidance method for launch vehicle [J]. Journal of Dynamics and Control, 2009,7(3):279-282(in Chinese).
[9] 宋征宇. 高可靠运载火箭控制系统设计[M].北京:中国宇航出版社,2014:3-15.
SONG Z Y.Highly reliable launch vehicle control system design [M]. Beijing: China Aerospace Publishing House, 2014: 3-15(in Chinese).
[10] 徐延万.控制系统[M].北京:宇航出版社,1989.
XU Y W.Control system[M].Beijing:Chinese Astronautics Press,1989 (in Chinese).

