基于模糊影响图的农产品供应链风险评估

张东东

（长安大学汽车学院，陕西 西安 710064）

前言

农产品种类繁多，数量庞大，生产具有地域性和季节性限制，且其具有鲜活性不易长时间保存。农产品是居民日常生活的必需品，由于农产品的上述特点，农产品供应链所面对的不确定性较大，风险也随之加剧。因此，农产品供应链风险的管理和提前风险评估研究对农产品流通有比较重要的意义。

1 模糊影响图的评价算法

模糊影响图是将模糊集理论与影响图结合，用模糊集理论描述节点的状态、频率及节点之间的关系。模糊影像图由三种类型的模糊集组成：状态模糊集、频率模糊集和模糊关系。当关系层确定后，模糊影响图在数值层上采用状态模糊集和频率模糊集描述节点的数据结构，在函数层上采用模糊关系描述变量间的关系[1]。

1.1 独立节点的频率矩阵

令X表示无前序节点的独立节点。假设节点X的可能状态向量为：PX={PX1,PX2,...,PXn}T。独立节点X的频率向量为：fX={fX1,fX2,...,fXn}T

独立节点 x的频率矩阵为：FX=(fX1×PX1)U(fX2×PX2) U...U(fXn×PXn)

1.2 非独立节点的频率矩阵

若X是由m个随机节点Y1Y2, Y3，…，Ym为其紧前节点的节点，FXP表示节点X的所有紧前节点频率矩阵的联合，则：FXP=FY1UFY2U... UFYm

若RXY1表示从Y1到X的模糊关系，则：RXY1=(PY11×PXi)U(PY12×PXi)U…U (PY1m×PXi)

节点 Ym 到节点 X 的模糊关系为：RXYm=(PYm1×PXi)U(PYm2×PXi)U…U (PYmn×PXi)

用PXP表示X的所有紧前节点模糊关系RXY1,…，RXYm的联合：RXP=RXY1URXY2U...URXYm

节点X的频率矩阵：FX=FXP°RXP

从价值节点 FX中选出使本行的和与对应概率的乘积是最大一行作为随机结果隶属度，即，生成风险变化的概率分布，则每一随机结果概率为：

2 建立农产品供应链风险结构

本文将农产品供应链主要的风险因素列举出来，将其分类为不同风险事件，风险事件导致风险后果以及风险损失。(如图1)每个风险因素都是独立的结点，风险因素是风险事件的紧前结点。在计算过程中，得出后面结点的结果时，其前面的结点被释放。

图1 农产品供应链风险影像图

3 基于模糊影响图的风险评估过程

3.1 定义模糊集

1）定义概率论域U={0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8,0.9,1.0}。在此基础上，定义三个频率模糊集：高(H)、中(M)、低(L)。其隶属度如下：

H={0.7|0.5,0.8|0.7,0.9|0.9,1.0|1.0}

M={0.3|0.2,0.4|0.8,0.5|1.0,0.6|0.8,0.7|0.2}

L={0|1.0,0.1|0.9,0.2|0.7,0.3|0.5}

2）描述不确定性的状态模糊集及隶属度定义如下：

很多={7%|0.5,9%|0.8,11%|1.0}

较多={3%|0.5,5%|1.0,7%|0.5}

较少={1%|1.0,3%|0.5}

对独立的结点，用模糊集不易描述时，将其模糊化：

大(G)=(大|1.0，中|0，小|0)

中(M)=(大|0，中|1.0，小|0)

小(B)=(大|0，中|0，小|1.0)

3）根据专家咨询确定节点间的模糊关系。首先描述独立节点的随机事件和频率估计，列出部分，如表1所示。其次，描述紧前、紧后节点关系。列出部分，如表2所示。

通过查找文献，得出风险因素的风险等级及发生概率。

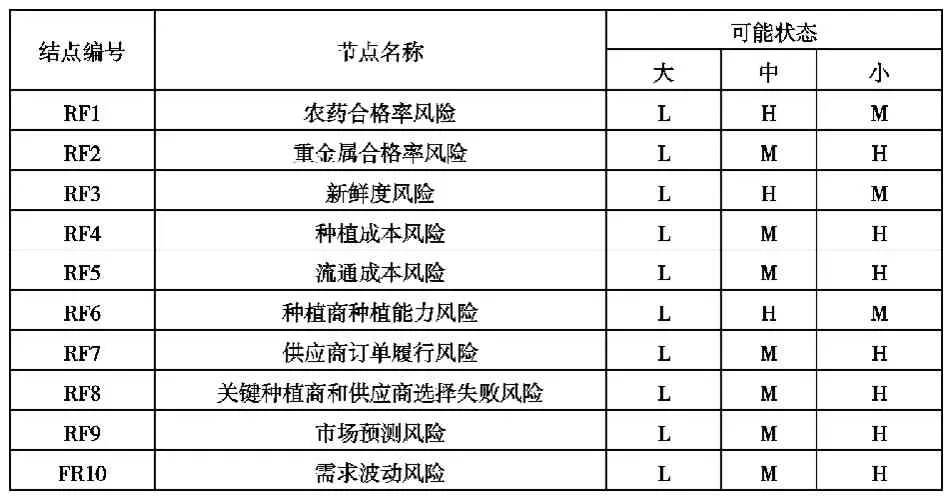
表1 独立节点状态及频率评估表

表2 风险节点之间的模糊关系

3.2 计算过程

Step1：计算风险因素结点的频率矩阵。

Step1-Step9公式中同样得到其它结点的频率矩阵。

Step2：计算风险事件结点的所有紧前结点(风险因素结点)频率矩阵的联合。

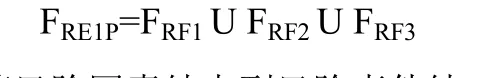
Step3：计算风险因素结点到风险事件结点的关系矩阵。

RRF1→RE1=(大×增加很多)U(中×增加较多)U(小×增加较少)

Step4：计算风险事件结点与所有紧前风险因素结点模糊关系矩阵的联合。

Step6：计算风险后果结点的所有紧前结点(风险事件结点)频率矩阵的联合。

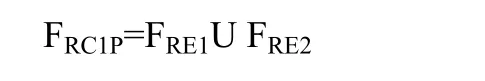
Step7：计算风险事件结点到风险后果结点的关系矩阵。

RRE1→RC1=(增加很多×增加很多)U(增加较多×增加较多)U(增加很少×增加很少)

Step8：计算风险后果结点与所有紧前风险事件结点模糊关系矩阵的联合。

Step9：计算风险后果结点的频率矩阵。

Step10：计算风险损失结点的所有紧前结点(风险后果结点)频率矩阵的联合。

Step11：计算风险损失结点的频率矩阵。

Step12：计算风险损失结点变动的概率。

从矩阵FRL中选取使本行的和与其所对应的频率的乘积在所有行中最大的一行，即

生成风险变化的概率分布，则每一随机结果的概率函数为：

Step13：计算风险损失的期望。

3.3 结果

根据风险损失的期望，就可以对日常农产品供应链小幅风险波动作出预测。根据农产品供应链的风险链，对风险因素、风险事件、风险后果、风险损失结点之间模糊关系的评估，计算得到在日常小幅波动下供应链的损失期望值大约为6.08%。

参考文献

[1] 孔媛媛,王恒山,朱珂,等.模糊影响图评价算法在供应链金融信用风险评估中的应用[J].数学的实践与认识, 2010, 40(21):80-86.

[2] 全吉,黄剑眉,张水波,等.基于风险链和模糊影响图的风险定性评估方法——以某海外EPC电力工程为例[J].南方能源建设, 2016,3(1):63-69.

[3] 郎济芳.蔬菜供应链风险评价研究[D].北京交通大学,2010.

[4] 张广胜.我国农产品供应链风险因素及对策探讨[J].浙江农业科学,2014, 1(3):0-315.

[5] 邓俊淼.农产品供应链中农户风险及防范机制研究[J].沈阳农业大学学报(社会科学版), 2008, 10(3):267-270.