互耦效应对不同阵列流型相关性的影响
杨颖,李伟东,薛翠薇,朱秋明,,廖志忠,陈小敏
(1.南京航空航天大学,江苏 南京 210016;2.中兴通讯股份有限公司,广东 深圳 518057;3.中国空空导弹研究院,河南 洛阳 471009)
1 引言
大规模多输入多输出(massive multiple-input multiple-output,massive MIMO)技术能够成倍地提高MIMO系统的通信容量和频谱资源利用率,已成为未来5G关键技术之一[1-3]。同时,智能终端设备体积越来越小,天线数目的增加将直接导致天线间距进一步减小。天线间距的减小,不仅会增加各天线之间的相关性,同时互耦效应变得显著,从而进一步影响天线空间相关性及系统性能[4-5]。
针对不同阵列流型的天线相关性,参考文献[6]推导了到达角服从拉普拉斯分布时,圆阵、线阵的天线相关性闭式解,并指出当线阵间距与圆阵半径相等时,圆阵相关性更小。参考文献[7]研究了入射角服从均匀分布时,不同角度扩展、角度均值对线阵及圆阵的天线空间相关性的影响。参考文献[8]推导了当入射角服从任意分布时,圆阵列的空间相关性通用表达式。参考文献[9]则针对任意角度谱,提出一种基于角度域脉冲采样的空域相关性近似算法。针对考虑互耦效应情况,参考文献[10]研究了天线耦合的影响机理,并推导了互阻抗、耦合矩阵的计算表达式。李忻等人[11]研究了互耦效应对平行线阵的影响,结果表明:互耦效应在特定情况下可能会降低阵列天线相关性。参考文献[12]进一步研究分析了拉普拉斯、均匀分布时互耦对圆型阵列空间相关性的影响情况,而参考文献[13]则分析了互耦对四元方阵空间相关性及信道容量的影响,并得出方阵具有良好的互补性、性能更优的结论。在此基础上,周杰等人[14]进一步针对三维空间域下的线阵、圆阵和面阵,推导了均匀分布和高斯分布时三者的空间相关性闭式解,并指出圆阵比线阵具有更好的抗互耦能力[14]。参考文献[15]则针对小角度扩展场景,分析了互耦对线阵、圆阵和面阵3种不同阵列流型空域相关性的影响。
基于上述研究,本文将针对更为通用的 Von Mises到达角分布,详细推导任意数目线阵、圆阵和面阵3种阵列流型的天线空间相关性通用闭合表达式,并分析耦合因素对天线相关性的影响情况,最终推导获得互耦效应下的空间相关系数表达式。
2 多天线系统模型
实际散射环境下,到达接收端的电波信号具有非全向性以及非均匀性的特点,从而导致不同位置的天线阵元接收信号具有不同程度的空间相关性。图1以线性天线阵列接收系统为例给出了电波信号入射模型,其中,0φ是散射体的到达角均值,Δφ是散射体的角度扩展。
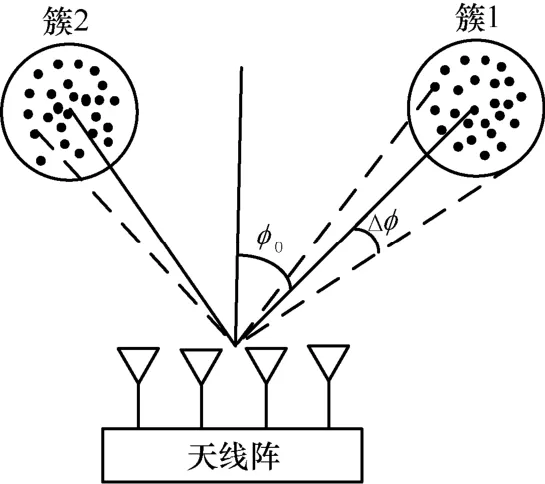
图1 多天线系统模型
N天线接收信号矢量可表示为:
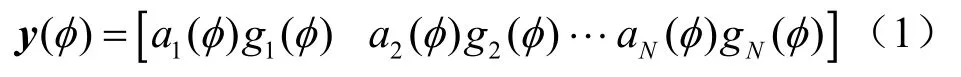
其中,表示各天线增益,为天线阵列流型矢量。第k根天线平均接收功率可表示为:
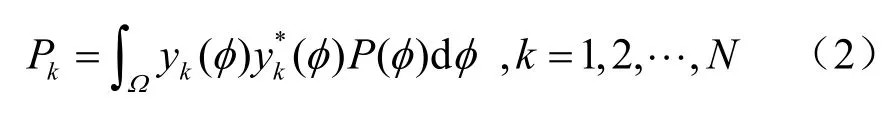
根据定义,第k根与第i根天线之间的空间互相关系数可表示为:

其中,P()φ表示到达波的功率角度谱。
目前较为常见的分布有均匀分布、高斯分布、拉普拉斯分布、余弦分布等,但Von Mises分布具有更强的灵活性[16],能够更好地描述接收信号到达角的空间分布,且可近似模拟余弦、截尾高斯等分布,故被广泛应用于无线信道建模。其概率密度函数为:
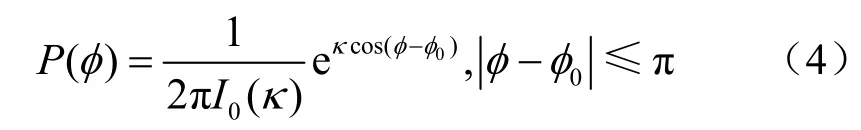
其中,κ因子表示角度谱的集中程度,I0(k)为第一类零阶修正贝塞尔函数。当κ=0时,该分布即全向均匀分布;当κ值较小时,与cosnα分布接近;当κ值较大时,与高斯分布非常接近。
图2仿真给出了κ=14.590 3、22.797 3、51.293 8情况下的 Von Mises理论分布,它们分别对应WINNER模型不同场景基站端的角度谱分布[17]。其中,κ=14.590 3对应市区微蜂窝场景;κ=22.797 3对应市区室内热点区场景;κ=51.293 8对应市区宏蜂窝场景。
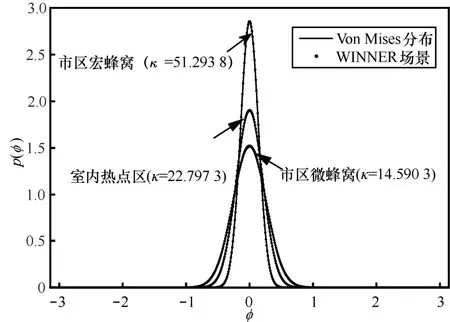
图2 不同κ值Von Mises分布
3 不同阵列流型相关性推导
3.1 3种阵列流型
本文主要针对均匀线型阵列(uniform linear array,ULA)、均匀圆型天线阵列(uniform circular array,UCA)和均匀面型阵列(uniform rectangular array,URA)3种流型阵列。图3分别给出了3种阵列流型的模型,ULA的导引矢量可表示为:
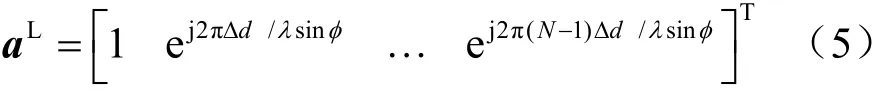
其中,N为接收端天线阵元数量,Δd为天线阵元间距,λ为入射信号波长,[]T⋅为转置矩阵。UCA的导引矢量可表示为:
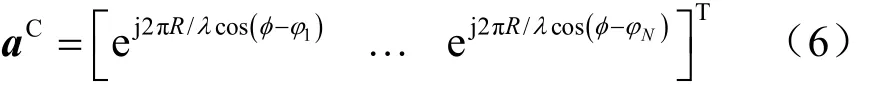
其中,为第n个天线单元的单位方位角。对于N×M阵元的URA天线阵列,其导引矢量为:
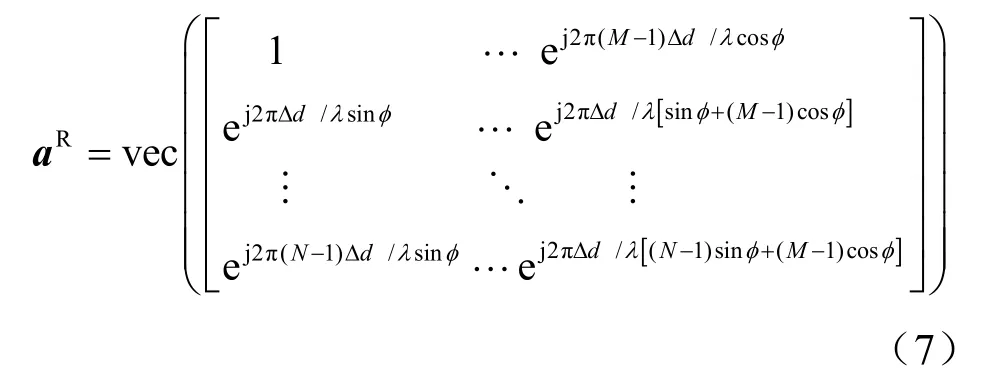
其中,运算符vec(·)可以将N×M的矩阵变换为的列矢量。
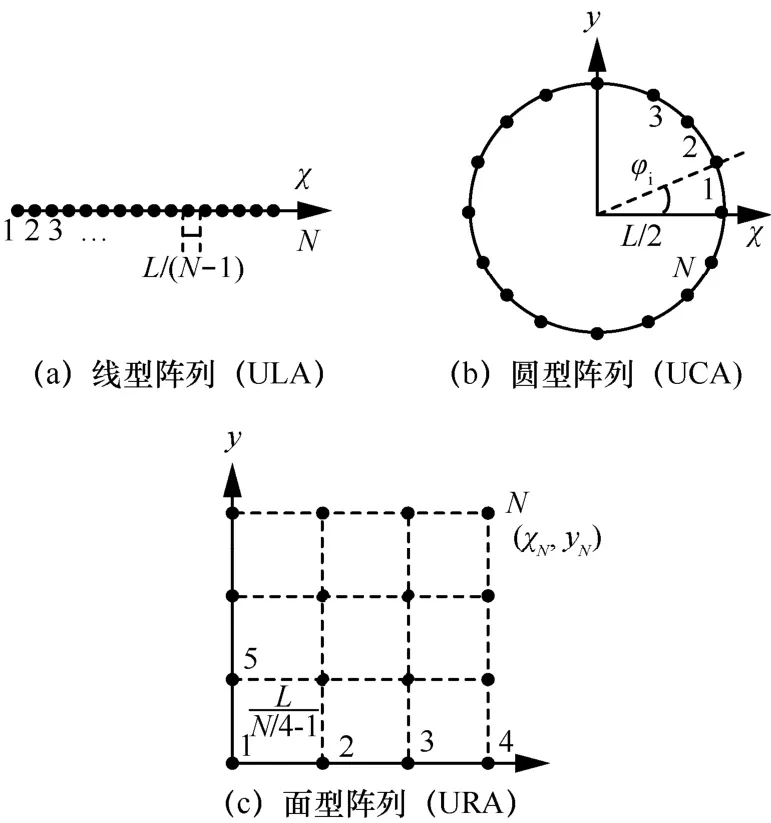
图3 不同天线阵列流型示意
为使下文推导得到的相关系数具有通用性,适用于任意天线阵列的空间相关性计算。首先将上述3种阵列任意两个阵元之间的矢量均表示为。对于线型阵列,;对于圆型阵列,对于面型阵列,
3.2 空间相关系数通用表达式
根据相关系数定义,假设天线接收信号的功率归一化,任意两个天线阵元k、i的空间相关系数可表示为:
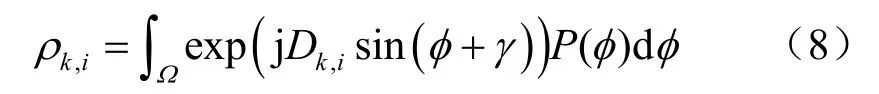
若到达角服从Von Mises分布,令变量代换x=φ+γ,则积分区间变为记式(8)可进一步推导为:

利用三角函数的傅里叶级数展开式[18]:
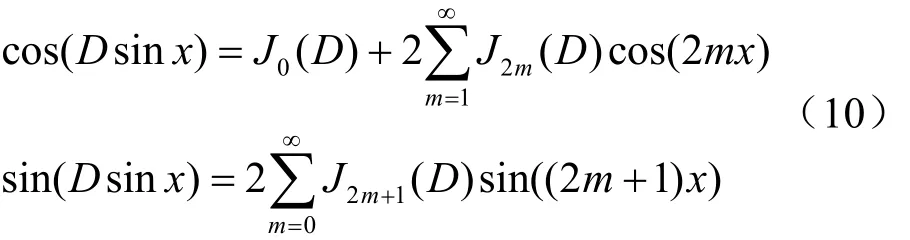
式(9)可简化为:

同理:
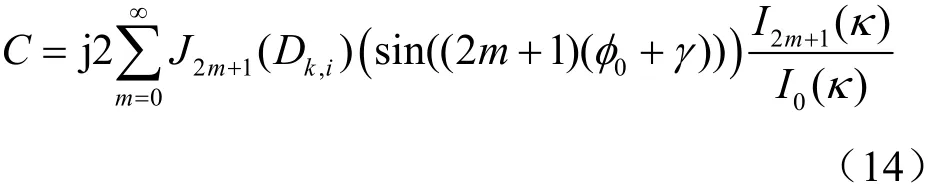
其中,表示第一类n阶Bessel(贝塞尔)函数,表示第一类n阶修正贝塞尔函数。
因此,式(8)最终可化简为:
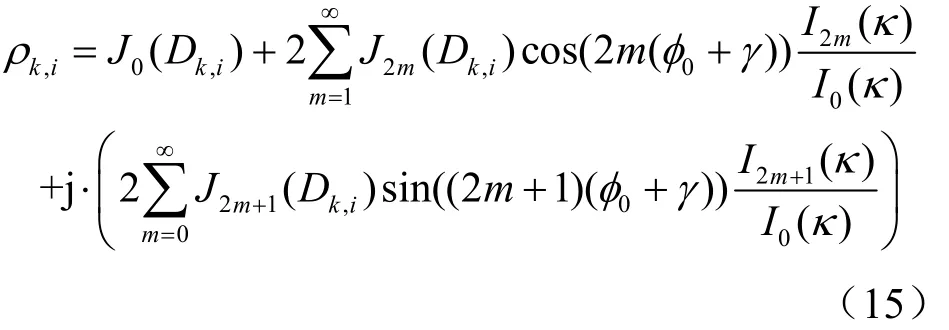
式(15)可用于评估不同阵列的空间相关系数。另外,实际传播环境下,到达接收端的电波信号角度扩展通常都比较小,比如3GPP标准公布的郊区宏蜂窝、市区宏蜂窝、市区微蜂窝3种场景下基站端信号角度扩展约小于5°[12],WINNER 模型提供的角度扩展参数一般也比较小[17]。据此可以对上述结果进行简化,首先将式(8)改写为:

令假定ν值很小,则式(16)可进一步化简为:
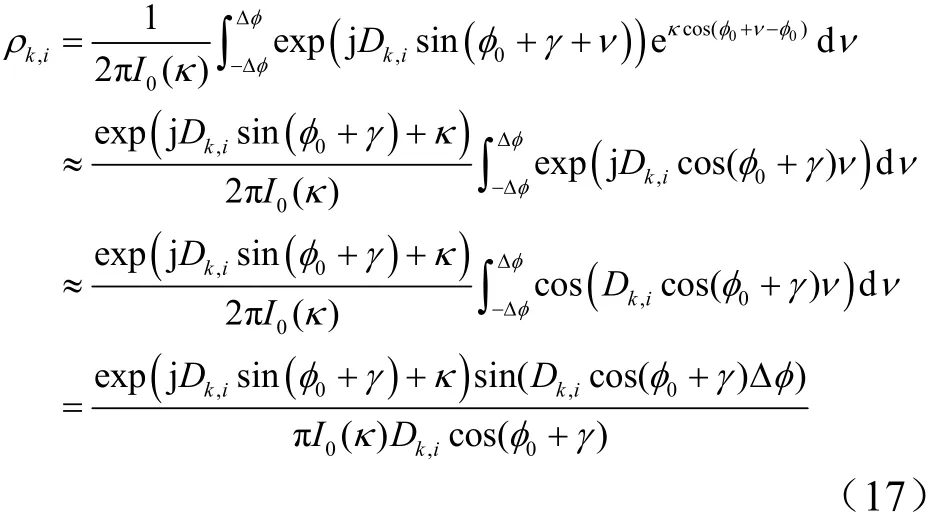
3.3 数值仿真分析
3GPP信道标准将移动通信场景主要分为郊区宏蜂窝、市区宏蜂窝和市区微蜂窝3种[12],其中郊区宏蜂窝的角度扩展为 5o,市区宏蜂窝的角度扩展为 8o和 1 5o,市区微蜂窝的角度扩展为19o。根据Von Mises分布及角度扩展定义,可得:
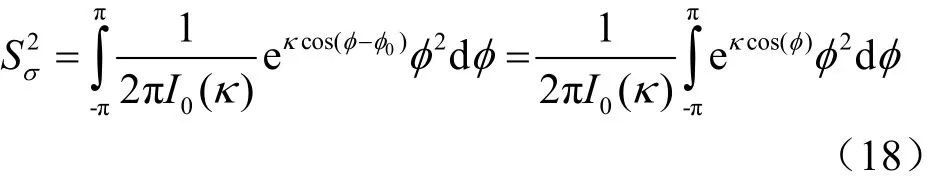
利用式(18)可获得不同场景下对应的κ值。当角度扩展较小时,二者关系近似可表示为:

所以,上述4种不同角度扩展对应的κ值分别为131、51、14、9。图4分别仿真了不同场景下各阵列流型的空间相关系数模值随归一化天线间距的变化情况。结果表明:3种阵列相关系数的近似表达式和解析式曲线基本吻合,验证了前文推导的闭式解和近似解的正确性;3种不同阵列流型布局相比,线型阵列相关性最大,大于圆型阵列,面型阵列相关性最小;在郊区宏蜂窝场景下的角度扩展小,近似表达式和解析式的误差较小,在市区微蜂窝场景下的角度扩展大,近似表达式和解析式的误差较大。
4 互耦效应影响分析
4.1 互耦效应对接收信号影响
当天线距离很近时,每个阵元上接收的电压信号感应出的电流信号,会激励出一个新磁场,并影响相邻阵元上的信号,导致天线阵列中的天线方向图发生畸变,即互耦效应。图5给出了接收端互耦等效网络模型,为天线阻抗(自阻抗),为负载阻抗,为天线阵列端口电压,为负载电压,Z为互阻抗矩阵。

图4 不同阵列流型天线相关性模值
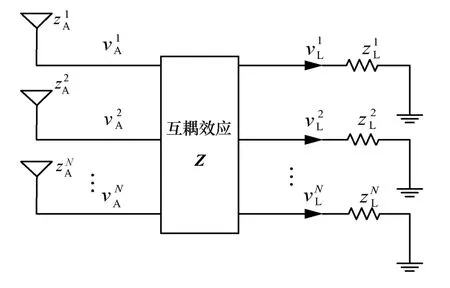
图5 接收端互耦等效网络模型
由于互耦效应使阵列天线信号之间发生串扰,考虑互耦因素的接收信号矢量,用C表示,可改写为:

其中,C为互耦矩阵。对于任意阵列流型,假设各天线特性相同、负载阻抗相等,互耦矩阵可由式(21)计算获得[10]:
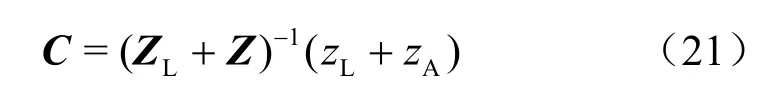
其中,ZL表示负载阻抗矩阵,Z为互阻抗矩阵。Z中任意两天线k、i的互阻抗可进一步由式(22)计算:
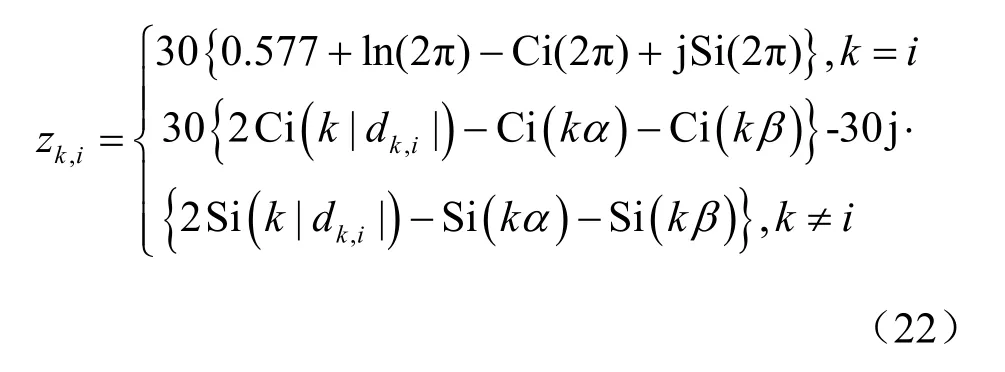
其中,为天线长度,积分函数Ci(x)、Si(x)可表示为:

针对图 3中 3种阵列流型布局(N=16,假设各阵元均为归一化的全向半波偶极子天线,天线长度。图 6给出了考虑互耦因素情况下,天线1接收信号矢量的模值,表示不考虑互耦的接收信号矢量模值。可以看出,不考虑互耦时的信号矢量模值恒为1;考虑互耦时,线型阵列增益失真最严重,其次为圆型阵列,且值均小于1,面型阵列增益失真最小,且部分增益值大于1。
4.2 互耦效应对相关性影响
互耦效应使负载电阻所接收到的电压改变,进而影响阵列天线的接收功率及空间相关性。互耦效应下任意天线阵列的天线单元接收功率为:

根据式(20)可得:
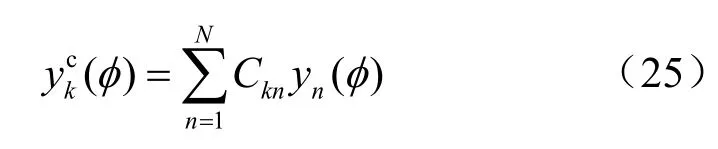
其中,Ckn表示互耦矩阵C的第行,因此式(24)可进一步推导为:

其中,ρn,m(上标 L/C/R省略)表示无互耦效应下任意两个天线的相关性。进一步,根据式(3)及式(26)最终可推导获得考虑互耦效应时,任意天线阵列的天线相关性(省略上标L/C/R)为:

其中,为:


图6 互耦效应对阵列信号矢量模值影响
假设到达角谱服从Von Mises分布,角度扩展为 1 80o,角度均值为 3 0o,图7仿真比较了在不同场景下考虑耦合与不考虑耦合时天线阵列相关性随归一化距离的变化情况。从图7中可以看出:考虑互耦时的相关性围绕无互耦时的相关性曲线上下波动,互耦效应在一定程度上降低了不同阵列天线的空间相关性;当天线间距增大到足够大时,互耦效应对阵列天线相关性几乎没有影响;当κ值很大时,互耦效应对相关性影响较小。

图7 耦合效应对空间相关性的影响
图8进一步仿真比较了耦合与无耦合情况下,3种天线阵列相关性随归一化距离的变化情况。从图8中可以看出:对于3种不同阵列流型,互耦效应均在一定程度上减小了其相关性;针对本文的天线布置,互耦效应对线型阵列相关性影响最大,其次为圆型阵列,对面型阵列影响最小。

图8 互耦效应对不同阵列相关性影响分析
5 结束语
本文假设入射信号角度谱服从 Von Mises分布,推导给出了任意数目线型、圆形和面型3种流型阵列的天线空间相关系数通用闭合表达式和近似表达式。在此基础上,通过研究分析互耦效应对阵列接收信号矢量的影响,推导获得了综合互耦因素的不同阵列天线空间相关系数的闭式解,并将其应用于3GPP信道标准传播场景。通过本文的研究可得出结论:对于天线面积受限的场合,面型布局的多天线系统可获得更佳的性能。该发现对天线阵列流型及阵元位置优化设计具有重要意义。后续笔者将进一步研究三维场景下不同阵列流型的天线空域相关性及互耦效应对其的影响。
参考文献:
[1]UMTS.Spatial channel model for multiple input multiple output: ETSI TR 125.996 V12.0.0[S].2014.
[2]WANG C X, HAIDER F, GAO X, et al.Cellular architecture and key technologies for 5G wireless communication networks[J].IEEE Communications Magazine, 2014, 52(2): 122-130.
[3]ZHANG J H, PAN C, PEI F, et al.Three-dimensional fading channel models: a survey of elevation angle research[J].IEEE Communications Magazine, 2014, 52(6): 218-226.
[4]GHOSH C K.A compact 4-channel microstrip MIMO antenna with reduced mutual coupling[J].AEU-International Journal of Electronics and Communications, 2016, 70(7): 873-879.
[5]AMIN M B, ZIRWAS W, HAARDT M.Advanced channel prediction concepts for 5G radio systems[C]// International Symposium on Wireless Communication Systems, Aug 25-28,2015, Brussels, Belgium.Piscataway: IEEE Press, 2015.
[6]DONG L J, MA J, ZHOU J, et al.Performance of MIMO with UCA and Laplacian angular distribution using correlation matrix[C]//IEEE International Conference on Wireless Communications, Networking and Mobile Computing, Sept 21-25, 2007,Shanghai, China.Piscataway: IEEE Press, 2007: 53-56.
[7]ALEM Y F, KHALID Z, KENNEDY R A.3D spatial fading correlation for uniform angle of arrival distribution[J].IEEE Communications Letters, 2015, 19(6): 1073-1076.
[8]KAMMOUN A, DEBBAH M, ALOUINI M S.Spatial correlation characterization of a uniform circular array in 3D MIMO systems[C]//2016 IEEE 17th International Workshop on Signal Processing Advances in Wireless Communications (SPAWC), July 3-6, 2016, Edinburgh, UK.Piscataway: IEEE Press, 2016: 1-6.
[9]朱秋明, 薛翠薇, 杨颖, 等.三维传播环境天线阵列空域相关性研究[J].系统工程与电子技术, 2017, 39(9): 1936-1941.ZHU Q M, XUE C W, YANG Y, et al.Spatial correlation characterization of antenna array in 3D propagation environment[J].Chinese Journal of Systems Engineering and Electronics, 2017,39(9): 1936-1941.
[10]CHEN K H, KIANG J F.Effect of mutual coupling on the channel capacity of MIMO systems[J].IEEE Transactions on Vehicular Technology, 2016, 65(1): 398-403.
[11]李忻, 聂在平.天线互耦对 MIMO 无线信道性能的影响[J].电波科学学报, 2005, 20(4): 136-141.LI X, NIE Z P.Effect of mutual coupling on the performance of MIMO wireless channels[J].Chinese Journal of Radio Science,2005, 20(4): 136-141.
[12]UMTS.Spatial channel model for multiple input multiple output: ETSI TR 125.996 V12.0.0[S].2014.
[13]ZHAO J, LI Y, SUN G.The effect of mutual coupling on capacity of 4-element squared antenna array MIMO systems[C]//2009 5th International Conference on Wireless Communications,Networking and Mobile Computing, Sept 24-26, 2009, Beijing,China.Piscataway: IEEE Press, 2009: 1-4.
[14]周杰, 陈靖峰, 邱琳.三维空间 MIMO 信道接收天线阵列互耦效应及系统容量分析[J].通信学报, 2012, 33(6): 1-10.ZHOU J, CHEN J F, QIU L.Effect of mutual coupling and antenna correlation on MIMO system in three-dimensional spatial channel models[J].Journal on Communications, 2012, 33(6): 1-10.
[15]薛翠薇, 朱秋明, 杨颖, 等.三维空间多天线相关性及互耦影响研究[J].电波科学学报, 2017, 32(1): 50-57.XUE C W, ZHU Q M, YANG Y, et al.On spatial correlation and effect of mutual coupling for multiple antennas under 3D environment[J].Chinese Journal of Radio Science, 2017, 32(1): 50-57.
[16]MARDIA K V, VOSS J.Some fundamental properties of a multivariate Von Mises distribution[J].Communications in Statistics-Theory and Methods, 2014, 43(6): 1132-1144.
[17]MEINILÄ J, KYÖSTI P, JÄMSÄ T, et al.WINNER II channel models[J].Radio Technologies and Concepts for IMT-Advanced,2009: 39-92.
[18]叶其孝, 沈永欢.实用数学手册(第 2版)[M].北京: 科学出版社, 2006: 713-714.YE Q X, SHEN Y H.Practical mathematics handbook(version 2)[M].Beijing: Science Press, 2006: 713-714.

