大规模MIMO上行链路的信号检测方法*
尹柏强,汪红梅,何怡刚
(合肥工业大学 电气与自动化工程学院,安徽 合肥 230009)
0 引 言
大规模多输入多输出(Multiple-Input Multiple-Output,MIMO)技术可以在不消耗额外带宽资源[1-3]的情况下,将频谱效率提高10倍及以上。目前,MIMO技术已经成为5G的关键技术之一[2]。接收解耦信号的检测方法[4]是MIMO系统的重要组成之一。在大规模MIMO系统中,基站处使用的天线数量达到数十甚至数百根,接收端接收的信号是多用户类型信号的叠加,接收端的信号检测复杂度远远大于传统的MIMO系统[5]。常用的检测方法中,基本线性检测方法如最小均方误差(MMSE)和迫零(ZF)等,以及基于连续干扰消除的非线性检测方法如多分支SIC(MB-SIC)[6-7]和多反馈SIC(MF-SIC)[8]等,都可以很容易地推广到大规模MIMO系统,并获得较好的系统性能。当基站的天线数量不断增加时,这些算法的计算复杂度会不断增大,传统的检测方法在大规模MIMO系统中的应用呈现瓶颈[9]。因此,降低大规模MIMO系统的计算复杂度,设计性能良好的检测算法,是当前的研究热点[10]。
分布式天线系统(Distributed Antenna System,DAS)能够降低路径损耗,提高覆盖范围和频谱效率[11],减少用户的能量消耗,改善传输质量,因此是5G异构网络系统架构采用的方式[12]。
针对分布式大规模MIMO系统的上行链路,提出了解耦信号检测(Decoupled Signal Detection,DSD)算法,在保证系统和速率性能的情况下,通过对系统和速率性能和浮点运算次数的仿真研究,大幅度降低了接收端信号检测的计算复杂度。结果显示,当用户类型和接收天线数量增加的情况下,计算复杂度显著降低。
1 分布式大规模MIMO信号模型
5G蜂窝网络是能够支持大量不同类型的设备同时传输数据信息的异构网络[13]。单个宏蜂窝小区可能需要支持10 000个或更多的低速率设备以及传统的高速率移动用户[14]。这就要求系统能够根据不同的数据速率要求,对诸如智能手机、平板电脑以及智能电网组件等用户进行联合用户分类。图1给出了5G异构网络集中式天线系统和分布式大规模MIMO系统上行链路信号模型。该系统有N个不同类型的活跃用户,D个远程天线阵列,基站处有B根接收天线,每个远程天线阵列有Q根天线,这些天线通过有线链路连接到基站。

图1 大规模的MIMO系统的上行链路信号模型
因此,接收天线的总数为Nr=B+DQ。需要说明的是,B、D和Q的选择取决于网络的特点和应用场景的类型。
城市场景中,使用多个集中式天线处理高密度的用户,而用分布式天线为其余设备提供服务。第n个用户类别的基数为|Cn|,表示第n个用户类别的用户数量,则活跃用户的总数为K=|Cn|。第n个用户类别的第k个用户通过Tk,n根天线发送Tk,n个子数据流。注意,这里系统需要满足Nr≥T,T是发射天线的总数,T=Tk,n。基站处接收到的信号矢量y为:

其中,Hn=[H1,nH2,n…H|Cn|,n]表示第n个用户类别的信道增益矩阵,sn=…表示第n个用户类别的发送信号向量。令H=[H1H2… HN],s=[… sTN],则式(1)可写为:

s的均值为零,协方差矩阵满足Ks=E[ssH]=diag( p),向量p表示每个发射信号的功率。为了简化随后的分析计算,假设所有天线阵列的平均功率为σs2,即Ks=σs2I。当信道增益矩阵H已知时,从式(2)可以知道,基站接收的信号是所有用户发射信号的耦合信号。如果根据用户的数据传输需求为每个用户类别使用不同的检测方法,则必须要将接收到的信号矢量y分离为每个用户类别的独立接收信号。
2 提出的解耦方法
在5G异构网络中,不同类别的用户通过分布式大规模MIMO信道发送并行数据流,然后在基站得到多用户叠加的数据流。为了有效地分离叠加的数据流,提出了解耦信号检测(DSD)算法。在信道矩阵已知的情况下,将第n个用户类别的接收信号与其他用户类别分离。将式(1)的接收信号写成:从式(3)可以看出,第n个用户类别具有用户间干扰。为了在第n个用户的检测过程中消去其他用户的影响,可以采用线性运算将接收到的信号矢量投影到与干扰用户信号正交或是近似正交的子空间,从而得到y的等效接收信号yn,yn∈CTn×1:
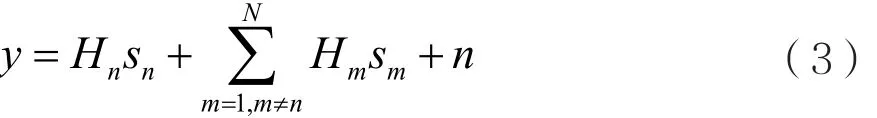

这样问题就转变成对目标矩阵An的求解。

为了计算An,构建除去第n个用户类别的信道矩阵 H~n:其中 H~n∈ CNr×(T-Tn),用户的发射天线数,则目标矩阵An满足:
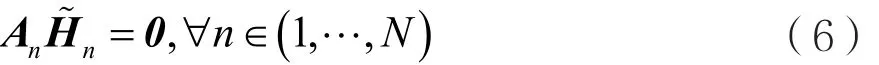
这样目标矩阵An的求解就转换为求解的左零空间基。求解的左零空间基常用的一种方法是执行SVD变换,这种方法虽然有效消除了用户间干扰,但是计算过程中没有考虑噪声的影响,存在较大的噪声效应。另外,计算过程中需要求解Nr×(T-Tn)阶矩阵的SVD变换,计算复杂度较大。
DSD算法使用信道反演方法和QR分解[15]计算矩阵An,具体做法如下。
首先,计算组合信道矩阵H的MMSE信道反演:
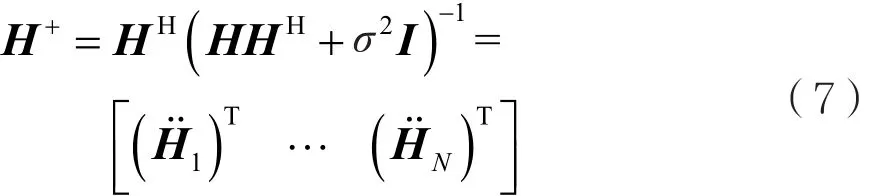
其中 σ2=,H+∈ CT×Nr,∈ CTn×Nr,是噪声向量的平均功率,则和近似满足:

接下来,对矩阵nH˙˙采用QR分解:
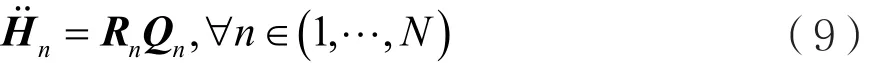
其 中Rn∈CTn×Tn是 上 三 角 阵, 矩 阵Qn∈CTn×Nr的所有行向量正交,由H~n的左零空间的近似正交基组成,即:

由此可以看出,Qn是目标矩阵An的一个很好的近似解。然后,将An=Qn和式(3)代入式(4),得到:
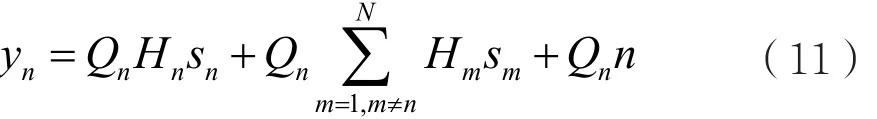

其中= Q H∈CTn×Tn是第n个用户类别解耦 n n后的等效信道矩阵,是等效噪声向量。值得注意的是,Qn不仅满足式(6)的零干扰约束,且适用于Nr<T的场合。由于在计算过程中考虑了噪声,所以它可以平衡用户间干扰和噪声效应。此外,计算式(7)的信道反演和式(9)的Tn×Nr阶矩阵QR分解的计算复杂度远低于SVD变换的计算复杂度。
3 DSD算法
3.1 基于线性检测的DSD算法
在线性检测器中,第n个用户的等效接收信号矢量使用线性滤波器来消除信道效应[16],采用ZF和MMSE两种线性检测方法:
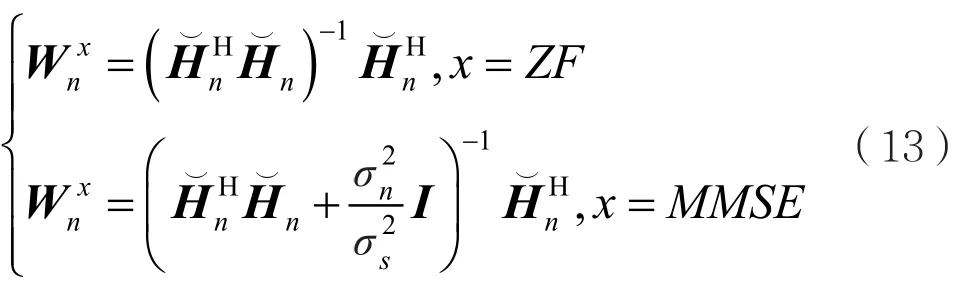
则sn的检测估计值为=C(yn),函数 C(x)返回最接近x的复数信号星座点。
3.2 基于SIC的DSD算法
在SIC接收机中,前一个检测器获得的分量被用于重建相应的信号矢量,然后将这个信号矢量从等效的接收信号中减去,以进一步降低下一个接收滤波器中输入信号的干扰,以此类推。最终,得到如式(14)所示的经过连续干扰消除后第i个阶段的接收信号:
其中对应于信道矩阵的列,sn的检测估计值由一组线性检测估计值组成。

3.3 基于MB-SIC的DSD算法
在第n个用户类别的多分支方案[17]中,假设有L个分支,每个˘分 支使用 一个列置换矩阵Pn,使用基于信道矩阵=的SIC接收机获得分支l的信号矢量,最终获得分支l的接收信号检测估计值为:

为了检测信号的质量,采用ML原则:
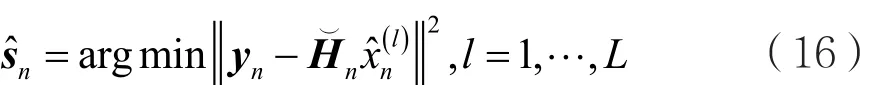
DSD算法表述如下:
初始化H、σ,获得接收信号y=Hs+n;
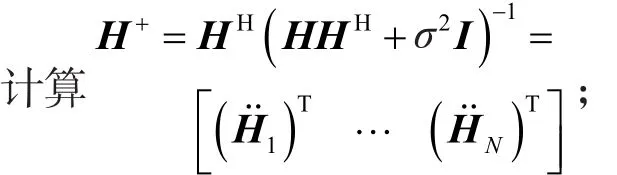
Do for 1 to N

4 仿真结果与分析
下面将对大规模MIMO系统上行链路DSD算法的和速率性能进行数值仿真,对比分析DSD算法和现有检测方法的计算复杂度。假设信道状态信息已知,仿真参数设置如下:对于CAS系统,路径损耗Lk=0.7,路径损耗指数τ=2,到基站的距离dk是分布在0.1~1之间的均匀离散随机变量,阴影效应σk=3 dB,发射和接收相关系数分别为ρrx=0.2,ρtx=0.4(当Tk,n>1);对于DAS系统,路径损耗Lk,j是分布在0.7和1之间的均匀离散随机变量,τ=2。每条链路到天线的距离dk,j是分布在0.1和0.5之间的均匀离散随机变量,阴影效应σk,j=3 dB,发射和接收相关系数分别为ρrx=0.2, ρtx=0.4。
4.1 和速率
图2是SNR=10 dB时,DAS和CAS两种天线系统的和速率和接收端天线数量关系的仿真结果。参数设置如下:N=16,|Cn|=1,Tk,n= 2,对于DAS系统,设置基站天线数。仿真结果表明,随着接收天线数量的增加,DSD算法的和速率越来越接近传统MIMO系统的和速率。当接收天线数量大于150时,DSD算法和传统检测方法的和速率基本相等,且DAS系统的和速率高出CAS系统约5 b/s/Hz。
图3比较了3种不同检测算法的和速率下限与接收天线数量关系的仿真结果。采用DAS系统,其他实验参数为K=30,N=3,|Cn|=10,Tk,n=1。仿真结果表明,随着接收天线数量的增长,不论是线性DSD算法还是非线性DSD算法,其和速率下限都可以达到传统MIMO系统。接收天线数量越大,和速率越接近,而非线性DSD算法的性能更好。
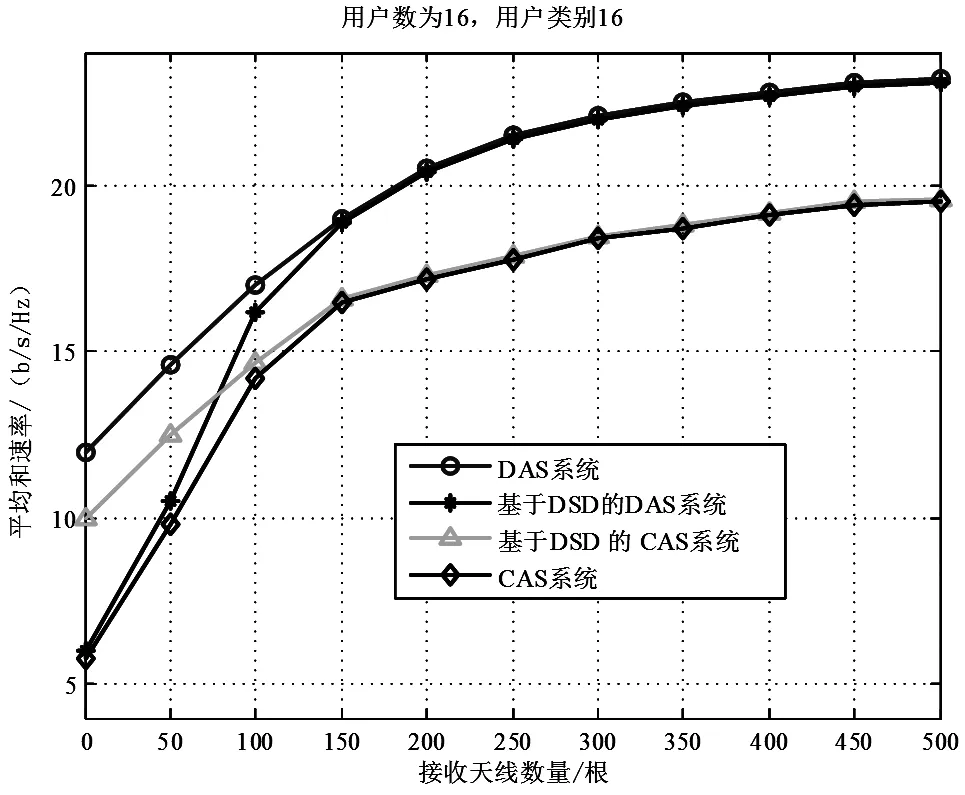
图2 和速率与接收天线数量的关系
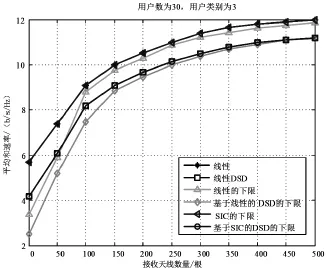
图3 和速率下限与接收天线数量的关系
图4 比较了下限和速率与SNR之间的关系。设置N=8,|Cn|=1,Tk,n=8,ρtx=0.85。对于DAS系统,取B=96,D=4,Q=8。仿真结果表明,DSD算法的和速率下限非常接近当所有用户的检测过程被同时执行时的下限。因为ZF DSD在解耦计算过程中考虑了噪声分量的MMSE矩阵,所以它是唯一性能优于其耦合计算部分的检测算法。
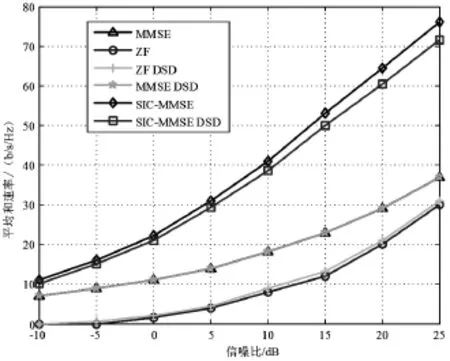
图4 和速率下限与SNR的关系
4.2 计算复杂度分析
以浮点运算次数来衡量DSD算法的计算复杂度,并与传统的检测算法进行比较。
图5反映了不同检测算法的浮点运算次数与用户类别之间的关系,设置活跃用户数K=100,每个用户的发射天线数量Tk,n=2,接收天线数量Nr=200。仿真结果表明,基于MB-SIC的DSD算法的浮点运算次数远远低于传统检测算法。随着用户类别数量的增加,所提算法在计算复杂度上的优势性越明显。

图5 计算复杂度与用户类别数量的关系
图6 反映了不同检测算法的计算复杂度与活跃用户数之间的关系。参数设置:用户类别N=5,每个用户的发射天线数量Tk,n=2,接收天线数量Nr=3KTk,n。结果表明,基于MB-SIC的DSD算法的计算复杂度远小于其传统检测方法。随着活跃用户数量的增加,基于MB-SIC的DSD算法在计算复杂度方面的优势愈发明显。
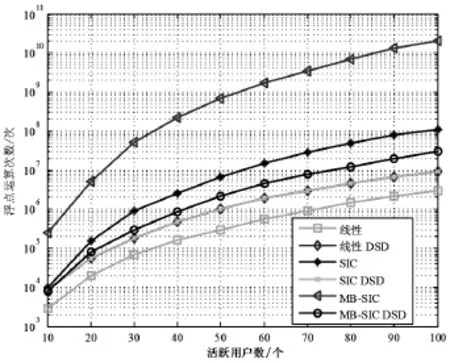
图6 计算复杂度与活跃用户数量的关系
可见,提出的基于MB-SIC的DSD算法,在不影响和速率性能的情况下,可以大幅降低系统的计算复杂度。
5 结 语
针对大规模MIMO系统上行链路的接收信号检测问题,提出了基于MB-SIC的DSD检测算法。在信道状态信息已知的情况下,基于MB-SIC的DSD算法可以将5G异构网络基站接收到的多用户耦合信号有效分离成独立的并行单用户信号。仿真结果表明,提出的基于MB-SIC的DSD算法在不影响系统性能的情况下,可以大幅降低系统的计算复杂度,为基于SIC的复杂检测方法在大规模MIMO系统的应用提供理论基础。为了简化计算,目前的研究是基于理想信道状态信息情况,但实际情形下系统的信道状态信息反馈是不准确的。因此,在信道状态信息不完备的情况下对DSD算法的研究十分必要。
参考文献:
[1] Marzetta T L.Noncooperative Cellular Wireless with Unlimited Numbers of Base Station Antennas[J].IEEE Transactions on Wireless Communicatio ns,2010,9(11):3590-3600.
[2] Larsson E G,Edfors O,Tufvesson F,et al.Massive MIMO for Next Generation Wireless Systems[J].IEEE Communications Magazine,2014,52(02):186-195.
[3] TR GPP.3GPP-LTE-2016 Technical Specification Group Radio Access Network:Evolved Universal Terrestrial Radio Access(E-UTRA):Further Advancements for E-UTRA Physical Layer Aspects(Release 13)[S].2016.
[4] 王晓天,杨龙祥.大规模MIMO信号检测算法研究[J].南京邮电大学学报(自然科学版),2015,35(03):52-56.WANG Xiao-tian,YANG Long-xiang.Research on Massive MIMO Signal Detection Algorithm[J].Journal of Nanjing University of Posts and Telecommunications(Natural Science Edition),2015,35(03):52-56.
[5] Higuchi S,Ahn C J.Reduced Complexity and Latency for a Massive MIMO System Using a Parallel Detection Algorithm[J].Ict Express,2017,3(03):119-123.
[6] Lamare R C D.Adaptive and Iterative Multi-Branch MMSE Decision Feedback Detection Algorithms for Multi-Antenna Systems[J].IEEE Transactions on Wireless Communications,2013,12(10):5294-5308.
[7] De Lamare R C,Sampaioneto R.Minimum Mean-Squared Error Iterative Successive Parallel Arbitrated Decision Feedback Detectors for DS-CDMA Systems[J].Communications IEEE Transactions on,2008,56(05):778-789.
[8] Li P,Lamare R C D,Rui F.Multiple Feedback Successive Interference Cancellation Detection for Multiuser MIMO Systems[J].IEEE Transactions on Wireless Communicati ons,2013,10(08):2434-2439.
[9] 吴同银.基于MF-SIC算法改进的大规模MIMO检测方法研究[D].合肥:安徽大学,2017:6-22.WU Tong-yin.Research on Detection Method Based on MF-SIC Algorithm in Massive MIMO Systems[D].Heifei:Anhui University,2017:6-22.
[10] 阳析,金石.大规模MIMO系统传输关键技术研究进展 [J].电信科学 ,2015,31(05):22-29.YANG Xi,JIN Shi.Overview of Key Technologies of Transmission in Massive MIMO System[J].Telecommunications Science,2015,31(05):22-29.
[11] Wang D,Wang J,You X,et al.Spectral Efficiency of Distributed MIMO Systems[J].IEEE Journal on Selected Areas in Communications,2013,31(10):2112-2127.
[12] Yuan S,Liang Q.3D Nested Distributed Massive MIMO:Modeling and Performance Analysis[J].Ad Hoc Networks,2016(58):6-12.
[13] Pervaiz H,Musavian L,Ni Q.Area Energy and Area Spectrum Efficiency Trade-off in 5G Heterogeneous Networks[C].IEEE International Conference on Communication Workshop,2015:1178-1183.
[14] Andrews J G,Buzzi S,Wan C,et al.What Will 5G Be?[J].IEEE Journal on Selected Areas in Communicatio ns,2014,32(06):1065-1082.
[15] Sung H,Lee S R,Lee I.Generalized Channel Inversion Methods for Multiuser MIMO Systems[J].IEEE Transactions on Communications,2009,57(11):3489-3499.
[16] Li X,Björnson E,Larsson E G,et al.Massive MIMO with multi-cell MMSE Processing:Exploiting All Pilots for Interference Suppression[J].Eurasip Journal on Wireless Communications & Networking,2017(01):1-15.
[17] Pham K,Lee K.Low-Complexity SIC Detection Algorithms for Multiple-Input Multiple-Output Systems[J].IEEE Transactions on Signal Processing,2015,63(17):4625-4633.

