超宽带信号的快速匹配追踪算法*
沈子钰,褚杭柯,唐川雁
(杭州电子科技大学 通信工程学院,浙江 杭州 310018)
0 引 言
传统采样定理要求采样频率是信号带宽的2倍以上,从而保证采样所得信号不失真。因此,在处理超宽带信号时,就会面临许多困难。压缩感知(Compressive Sensing,CS)[1]是一种新的稀疏信号采样和重建理论。该理论中,信号采样和压缩能同时完成,使得系统能够低于奈奎斯特采样频率采样,降低了系统的数据采样和储存成本,适合应用于超宽带通信系统。Jose[2]是最早研究压缩感知应用于超宽带的学者之一。文献[2]中提到了两种超宽带稀疏信号的表示方式,一种用时域稀疏字典来表示,即单位矩阵,一种用多径分集字典来表示,能够更加稀疏地表示超宽带信号,因此被更多采用。但是,多径分集字典由超宽带脉冲波形位移产生,相邻原子之间的相关性较高,在使用匹配追踪算法时,会对原子的正确选择造成一定干扰。压缩采样匹配追踪(Compressive Sampling Matching Pursuit,CoSaMP)[3]算法、稀疏度自适应匹配追踪(Sparsity Adaptive Matching Pursuit,SAMP)[4]算法和正则化正交匹配 追 踪(Regularized Orthogonal Matching Pursuit,ROMP)[5]算法,每次迭代都会选取多个原子,使得选取相邻原子的可能性加大而产生误选。广义正交匹配追踪(Generalized Orthogonal Matching Pursuit,GOMP)[6]每次迭代选择L个原子,L被称为迭代步长。L越大,GOMP发生原子误选的可能性越高。正交匹配追踪(Orthogonal Matching Pursuit,OMP)算法[7]由于每次迭代只选择一个原子,所以重构精度没有明显降低。但是,OMP的迭代次数过多,需要大量计算时间,所以L在一定范围内时,GOMP更加适合应用于超宽带通信。
本文在GOMP算法的基础上,针对超宽带信号稀疏表示的特点做出改进,尽可能避免一定区间范围内同时选择多个原子。仿真实验表明,本文算法能够在运算时间接近GOMP的情况下,获得更高的重构精度。而相对于OMP而言,本文算法能在保证重构精度的同时,有效节省运算时间。
1 压缩感知理论
压缩感知理论指出:假设信号x∈Rn在n×n维的稀疏字典下可以被稀疏表示,稀疏度k<n,通过m×n维的测量矩阵Φ随机采样后得到m(k<m<n)维的观测向量y为:

其中Θ称作传感矩阵,向量α是信号x在稀疏字典Ψ下的稀疏表示。由于m<n,通过观测向量y和测量矩阵Φ无法直接求信号x,所以将其转化成如下最优化问题:
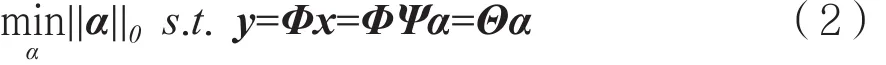
其中,||α||0表示α的l0范数。式(2)中的优化问题是一个NP-Hard问题,通常在传感矩阵满足约束等距性质(Restricted Isometry Property,RIP)[8]的条件下,将式(2)中l0范数优化问题转化为如式(3)所示的l1范数优化问题:
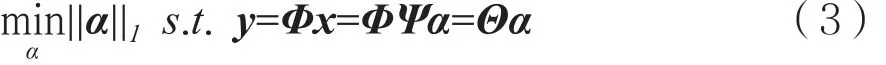
通过相关重构算法,如OMP算法、基追踪(Basis Pursuit,BP)算法[9]和迭代硬阈值(Iterative Hard Thresholding,IHT)算法[10]等,就可以利用已知的观测向量y和传感矩阵Θ求得稀疏表示向量α,再进而求出信号x。
2 超宽带信号的快速匹配追踪算法
2.1 算法分析
首先介绍多径分集字典。脉冲超宽带信号经过多条不同时延和衰落的路径到达接收机,接收信号就由这些分量组合而成。稀疏字典的设计应该尽可能考虑和利用被稀疏表示信号的结构与特征。所以,文献[2]提出了一种稀疏表示基,即:

其中n∈{1,2,…N},p(t)表示超宽带发射脉冲波形,τ表示理论上的采样时间间隔。若N表示一次观测的总采样点数,则一次观测的总时长为T=Nτ。接收信号在此稀疏字典下可表示为:

其中,K既代表信号多径的数目,也代表信号x的稀疏度,{α(nl)}为各个多径分量的幅值。超宽带信号占用的带宽极宽,具有高多径分辨率,可认为多径分量重叠的概率很小,且只有一小部分的多径分量幅值较大。因此,超宽带信号在该稀疏字典下可以被稀疏表示,且相对于时域稀疏字典,这种表示方法的结果更加稀疏。
目前,关于压缩感知应用于超宽带的研究中,大多数采用了多径分集字典作为稀疏矩阵。因为多径分集字典相比于时域稀疏字典,更能充分利用脉冲超宽带信号的稀疏性。使用时域稀疏字典时,无论采用何种重构算法,重构精度都比较低。因此,实际应用中采用时域稀疏字典是不可行的。
然而,在使用多径分集字典时,CoSaMP、SAMP、ROMP均出现了较大误差,原因是多径分集字典的相邻原子相关性很高,匹配追踪类算法采用内积的绝对值大小作为原子筛选的标准。正确原子相邻的位置的内积绝对值往往也较大,若一次迭代中选择很多原子,那么在匹配追踪的原子筛选过程中容易选择正确原子的相邻原子,从而产生误选。
文章第3节的图1可以看出,随着GOMP迭代步长的增大,重构精度明显下降。但是,当字典为单位矩阵时,迭代步长的增大并不会造成重构精度明显下降[6]。由此可以证明,多径分集字典对迭代步长较大的匹配追踪算法会有一定影响,问题的根本原因是正确原子的相邻原子与残差的内积值较大,致使其容易在同一次迭代中被选中。解决这一问题的办法是在匹配原子的过程中尽量避免同一次迭代选中相邻原子。基于这样的目的,本文提出了一种算法,使得同一次迭代所选原子保持一定距离。若只选择正确的原子,再经过正交化处理,那么下一次迭代中残差与其相邻原子的内积值会明显减小,从而可以有效降低误选的可能性。
此外,本文算法将GOMP的迭代停止条件改为||rt-rt-1||2/||rt-1||2<ε或者满足t>K,其中t代表迭代次数的序号,rt代表第t次迭代后的残差,K是允许的最大迭代次数,ε为常数。也就是说,当残差的相对变化率小于一定数值时,认为匹配追踪已经完成。该条件增强了算法的自适应性,在信号稀疏度不明确的条件下也能使用该算法。
2.2 算法步骤
GOMP的计算复杂度比OMP低,在步长L不大时,其重构精度甚至略微优于OMP,所以显然更适合应用在超宽带的高速通信中。本文在GOMP的基础上,针对算法的不足作出改进,使得在算法复杂度没有明显提高的前提下提高重构精度,使算法更具有应用价值。
下面是本文提出算法的具体步骤:
输入:感知矩阵Θ=ΦΨ,观测向量y,每次迭代选取的原子个数L,最大迭代次数K;
(1)初始化:残差r0=y,已选原子索引集合Λ0=∅,已选原子集合A0=∅,迭代次数t=1;
(2)计算 uj=|〈rt-1,Θj〉|,j∈ {1,2,…N}表示 Θ中各原子(列向量)的序号和u中各元素的序号;
(3)按照向量u各元素的值从大到小依次选择对应序号的原子。在此过程中,若某原子与任意已被选中原子的序号之差的绝对值小于S,则该原子被舍弃,直到L个原子被选中,再进行下一步;
(4)将这L个原子对应的序号构成集合J,Λt=Λt∪ J,At=At∪ θJ,θj代表第 j个原子;
(5)利用最小二乘法计算被选原子对应的系数 αt=(At)-1y;
(6)更新残差rt=y-At(At)-1y;
(7)t=t+1,如果||rt-rt-1||2/||rt-1||2<ε或者满足t>K,则进行下一步;否则返回第2步继续迭代;
(8)根据被选原子的系数αt和稀疏矩阵Ψ,可以得到原始信号x=Ψαt;
输出:原始信号x。
3 仿真与分析
本文通过仿真实验验证算法的性能。选取原始信号为IEEE802.15.3a CM1模型下1 024×1的脉冲超宽带多径信号,测量矩阵为M×1 024的高斯随机矩阵,M为观测点数,本文算法中S的取值为3,ε取值为0.1。参照文献[2]中的评价标准:若重构误差小于原始信号能量的1%,即||y-<0.01||,则认为信号被成功重构。本文采用信号重构成功的概率作为重构精度的衡量指标。仿真环境为Intel i5-5200U CPU,8G RAM,Windows 10 64位操作系统,采用Matlab 2016b仿真。
图1和图2分别表示迭代步长L从1变化到15过程中,GOMP算法和本文算法运行时间和重构精度的对比,其中稀疏字典都采用多径分集稀疏字典。
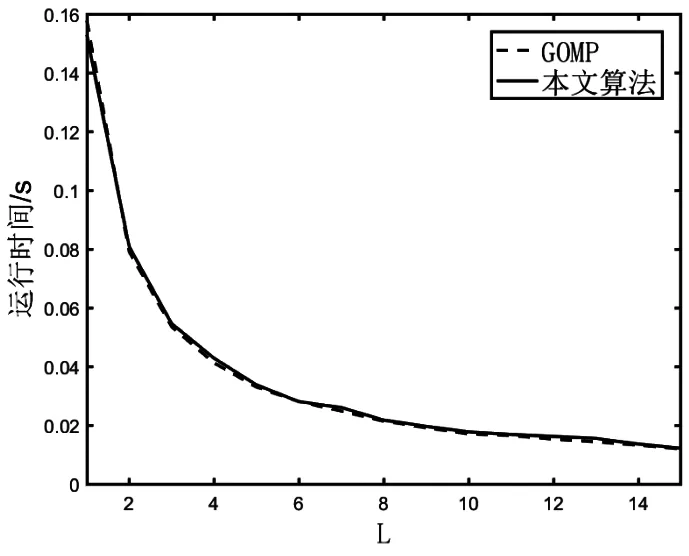
图1 两种算法运行时间与迭代步长的关系
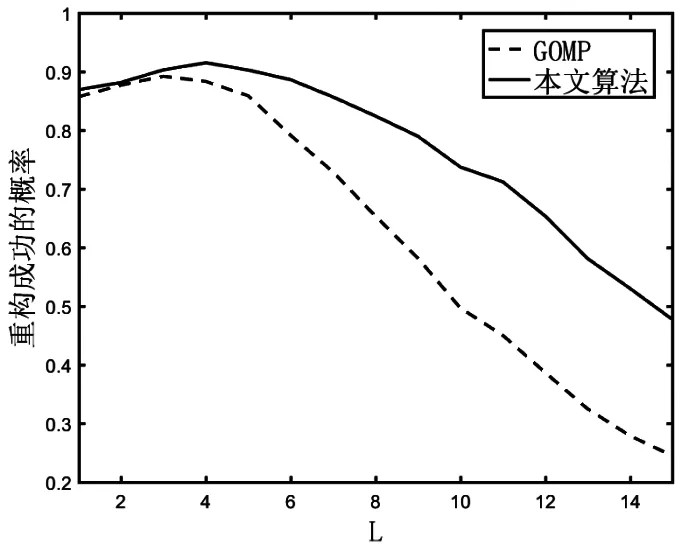
图2 两种算法重构成功的概率与迭代步长的关系
由图1和图2可得以下结论:(1)本文算法与GOMP算法的计算复杂度相近,迭代次数是影响整体计算复杂度的最主要因素。相比OMP算法(即GOMP算法L=1时),GOMP和本文算法在计算复杂度上有明显优势。(2)当随机采样点数为256时,本文算法在迭代步长L=4时成功重构信号的概率最大,GOMP算法在L=3时成功重构的概率最大。相比于OMP算法和GOMP算法,本文算法在重构精度和计算复杂度两个方面都有一定优势。(3)当迭代步长过大时,GOMP和本文算法的重构精度都会下降,但显然本文算法受到的影响更小,所以同等精度要求下,本文算法可以选择更大的迭代步长。
表1为观测点数M不同的情况下,不同重构算法成功重构原始信号的概率。分别检测OMP算法、GOMP算法(L=3、L=6)以及本文算法(L=3、L=6)在稀疏字典为多径分集字典的情况下成功重构的概率。各种情况均重复10 000次,最后得到如表1所示的统计结果。从表1的数据中可以看出,当要求重构成功概率为1时,OMP和本文算法(L=3)所需的观测点数M最少,但本文算法运行时间约是OMP的1/3。GOMP需要的观测点数最多,不利于降低采样率,也增加了重构所需的时间,说明本文算法相比OMP和GOMP具有更佳的性能。在实际应用中,可以根据需求选择合适的步长,从而在满足采样率和重构精度要求的前提下节省算法的运行时间。

表1 不同M取值下各算法重构成功的概率
4 结 语
本文介绍了用于稀疏表示超宽带信号的多径分集字典,分析了CoSaMP、GOMP等算法出现原子误选的原因,并针对OMP和GOMP两种算法在超宽带应用中的不足作出改进,限制被选原子之间的序号差,减少原子误选的发生,弥补多径分集字典的不足,从而选择更大的迭代步长。仿真实验证明,
该算法在运行时间和重构精度两个方面都获得了一定改善。
参考文献:
[1] Donoho D L.Compressed Sensing[J].IEEE Transactions on Information Theory,2012,52(04):1289-1306.
[2] Paredes J L,Arce G R,Wang Z.Ultra-Wideband Compressed Sensing:Channel Estimation[J].IEEE Journal of Selected Topics in Signal Processing,2007,1(03):383-395.
[3] Needell D,Tropp J A.CoSaMP:Iterative Signal Recovery from Incomplete and Inaccurate Samples[J].Applied &Computational Harmonic Analysis,2008,26(03):301-321.
[4] Do T T,Lu G,Nguyen N,et al.Sparsity Adaptive Matching Pursuit Algorithm for Practical Compressed Sensing[C].Signals,Systems and Computers,2009:581-587.
[5] Needell D,Vershynin R.Uniform Uncertainty Principle and Signal Recovery via Regularized Orthogonal Matching Pursuit[J].Foundations of Computational Mathematics,2009,9(03):317-334.
[6] Jian W,Kwon S,Shim B.Generalized Orthogonal Matching Pursuit[J].IEEE Transactions on Signal Proces sing,2012,60(12):6202-6216.
[7] Pati Y C,Rezaiifar R,Krishnaprasad P S.Orthogonal Matching Pursuit:Recursive Function Approximation with Applications to Wavelet Decomposition[C].Signals,Systems and Computers,2002:40-44.
[8] Donoho D L,Huo X.Uncertainty Principles and Ideal Atomic Decomposition[J].IEEE Transactions on Information Theory,2002,47(07):2845-2862.
[9] Chen S S,Donoho D L,Saunders M A.Atomic Decomposition by Basis Pursuit[J].Siam Review,2001,43(01):129-159.
[10] Donoho D L,Tsaig Y,Drori I,et al.Sparse Solution of Underdetermined Systems of Linear Equations by Stagewise Orthogonal Matching Pursuit[J].IEEE Transactions on Information Theory,2012,58(02):1094-1121.

