基于Curvelet变换的指纹图像去噪
张建明,邱晓晖
(南京邮电大学 通信与信息工程学院,江苏 南京 210000)
0 引 言
近年来,小波变换理论凭借其对信号的特殊时、频分析能力,在信号、图像等领域得到了快速发展,在图像去噪领域也得到了广泛应用。然而,由一维小波张量积张成的小波因其固有的各向同性和有限的方向选择特性,仅适合刻画点状奇异信息,难以对二维图像信号中含有的各种直线、曲线等线奇异信息进行有效表示。因此,针对小波变换对二维图像及更高维信号表示的不足,E.J.Candes和Donoho于1998年提出了脊背变换(Ridgelet变换)[1],这一变换在小波的基础上添加了方向参数,在继承小波良好的时频分析能力的同时具有更好的方向选择性,能够很好地表达直线奇异信息,但是对曲线信息的描述具有局限性。1999年,E.J.Candes和Donoho提出第一代Curvelet变换理论[2],它是建立在脊背变换理论基础上的新的多尺度几何表示方法,能够很好地表示曲线特征信息并拥有更强的方向选择特性。2002年,E.J.Candes和Donoho又搭建出第二代Curvelet变换的框架体系[3],并于2005年提出基于第二代Curvelet变换的快速离散算法[4],大大降低了第一代Curvelet方法实现的计算冗余度和复杂度。
指纹图像具有丰富的曲线特征信息,因此将Curvelet变换方法应用于指纹图像去噪可以更好地保留原始信号的边缘及曲线等线性特征,提升去噪水平和视觉效果。因此,文中采用基于Wrapping的第二代快速离散Curvelet变换算法,通过自适应选取子带阈值并对变换后的各个尺度各个方向上的Curvelet系数采用一种新的阈值函数进行处理。
1 第一代Curvelet变换
第一代Curvelet变换理论是充分建立在Ridgelet变换理论的基础上的,其实质是在Ridgelet变换域上进行局部多尺度分析。Ridgelet变换对含有直线奇异信息的函数具有良好的逼近能力,但对奇异曲线的逼近能力有限。而第一代Curvelet变换提出在所有的尺度上进行Ridgelet变换,充分利用了多尺度分析的优势,具备了对奇异曲线优秀的表示能力,能够极小地逼近误差衰减阶。
Curvelet变换过程一般由子带分解、平滑分割、脊波分析三个部分组成。其数字实现过程如图1所示。

图1 第一代Curvelet变换的分解过程
首先将函数f用滤波器P0分成不同的子带(P0f,Δ1f,Δ2f,…),P0f表示f的低频部分,Δsf表示尺度2-s下的高频子带信息;然后定义方形区域Q=[K1/2s,(K1+1)/2s]×[K2/2s,(K2+1)/2s]对Δsf通过平滑窗口函数WQ进行分割,实现对不同尺度子带函数的平滑;接着通过定义传输算子TQf(m,n)=2sf(2sm-k1,2sn-k2)对每个平滑分块的二进方块Q进行重正归化,可以得到gQ=(TQ)-1(WQΔsf);最后对gQ进行正交Ridgelet变换,从而实现Curvelet变换。
2 第二代Curvelet变换
第一代Curvelet变换的数字实现十分复杂,计算冗余度高。因此Candes等提出了第二代Curvelet变换。第二代Curvelet变换与第一代有着截然不同的架构体系,第一代Curvelet变换的核心思想是将曲线分割到一个个足够小的方块中,然后把方块中的曲线近似成直线看待,最后对其进行局部的Ridgelet分析。而二代Curvelet变换在实现过程中完全无需用到Ridgelet变换,两代变换间的唯一相同点在于紧支撑、框架等抽象数学意义。
2.1 连续Curvelet变换
Curvelet变换在二维空间R2中实现,x为空间位置参量,定义在尺度2-j、方向θl、位置参数(k1,k2)∈Z2处的Curvelet为:
φj,l,k(x)=φj(Rθl(x-xkj,l))
(1)
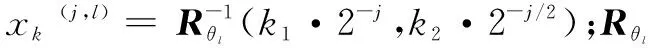
因此,同小波理论一样,Curvelet变换可以以内积形式定义为:
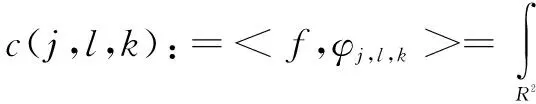
(2)
其重构公式为:
(3)
2.2 离散Curvelet变换
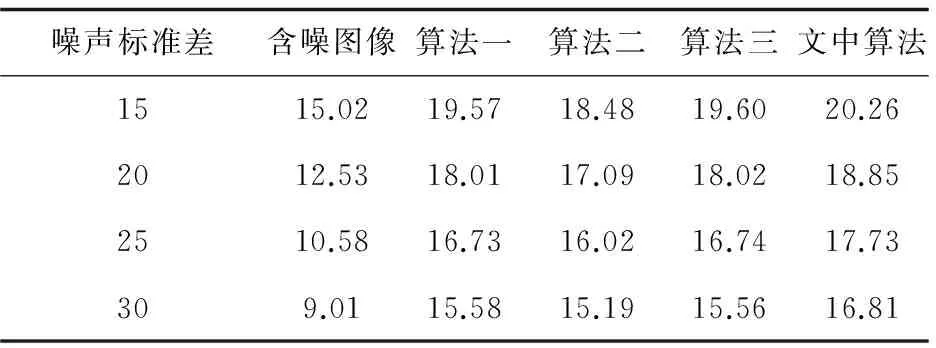
以笛卡尔坐标系下的f[t1,t2](0≤t1,t2 (4) φj(w1,w2)=φ(2-jw1)φ(2-jw2),0≤φ≤1 (5) 定义: Vj(w)=V(2⎣j/2」)w2/w1 (6) 然后用Wj和Vj定义笛卡尔坐标系下的窗函数: (7) 定义: (8) 此算法的核心思想是:环绕原点进行Wrap,在任意区域位置上,采取周期化技术逐一映射到原点的仿射区域。具体算法过程如下: (3)Wrap上步得到的乘积结果,围绕原点包装用下式局部化: (9) 其中,0≤n1≤L1j,0≤n2≤L2j。 与经典的小波理论相比,Curvelet变换作为一种新型多尺度几何分析方法在对二维图像中的各种直线或者曲线等边缘信息进行分析时具备更明显的优势,而且拥有更高的逼近精度和更好的稀疏表达能力[5],因此将Curvelet变换引入线状特征信息明显的指纹图像中能够更好地消除图像噪声,同时保留边缘特征和细节信息。由Curvelet变换理论可以得到如下结论:因为Curvelet系数是由图像函数f与Curvelet基函数φj,l,k作内积产生的,所以当Curvelet基函数与图像边缘轮廓的方向一致时会产生比较大的系数,相反,图像中含有的噪声与基函数内积后会产生较小的Curvelet系数[6]。因此为了去除噪声,可以采用阈值方法保留大的系数,舍弃较小的系数,而且不损失边缘细节。目前通常采用的阈值处理方法有软阈值、硬阈值、软硬折衷阈值[7]等。因此,阈值和阈值函数的合理选取成为Curvelet去噪方法中至关重要的两个决定性因素。 λj=kσσj (10) 其中,k为各层子带中设置的尺度依赖常数[8-9]。k为实验确定的经验数值,一般在低尺度上较小,高尺度较大。阈值选取合理是阈值型去噪方法中的关键一步,如果阈值选取过大,会使图像自身的边缘纹理等重要细节特征丢失,而阈值选取过小,会使噪声无法得到有效抑制。文中在式10的基础上提出新的自适应阈值选取方案: (11) 其中,α(α∈(0,1))为自适应尺度调节因子;J为分解的总层数。上式中分别以αj和(1+αj)在各低尺度和最高尺度替换式10中确定的经验数值k,从而通过调节参数α的大小使得各层阈值得到自适应调节,避免了原阈值选取不够灵活的缺陷,使得各高频子带的噪声Curvelet系数和原始图像信号Curvelet系数能够更好地得到分离,达到更好的去噪效果。 文中J和α的取值分别为6和0.46。 (12) (1)运用基于Wrapping的快速离散算法,对含噪图像进行Curvelet变换,从而得到各尺度各方向的Curvelet系数cD(j,l,k); 为验证基于Wrapping的自适应阈值和改良折衷阈值函数的算法的优越性,选取指纹数据库中340×389的指纹图像作为实验对象。对比三种算法的去噪结果:Curvelet硬阈值去噪、Curvelet软阈值去噪、Curvelet软硬折衷阈值去噪(简称算法一、二、三)。选取峰值信噪比和去噪后的视觉效果作为评价指标。 PSNR的定义为: (13) 图2是指纹图像在标准差σ=20的高斯白噪声情况下,利用各种去噪算法得到的指纹图像。可以看出,几种Curvelet去噪算法都能对噪声起到很好的抑制作用。但算法二的去噪效果相较于其他几种算法视觉效果较差,出现了轻微的模糊失真。从表1的软阈值去噪后的PSNR值略低于其他几种算法也可得到验证。因此在实际应用中更倾向于硬阈值去噪方法。文中提出的方法利用自适应阈值和改进阈值函数的方法更好地将噪声Curvelet系数去除,从而更为有效地保留了各个高频子带原始指纹图像Curvelet系数,保持了图像的边缘部分和纹理细节信息,改善和提升了视觉效果,去噪效果更接近原指纹图像。 表1给出了指纹图像加入不同方差的高斯白噪声时,各种去噪算法的峰值信噪比的比较结果。可以看出,算法一,三去噪水平相当,但要优于算法二。文中算法使得去噪后的信噪比相较于其他三种算法具有较大的提高,去噪效果明显。 表1 指纹含噪图像和去噪后指纹图像峰值信噪比对比结果 dB 文中提出一种改进的多尺度自适应阈值选取方案,并与新型的阈值函数相结合,采用基于Wrapping的快速离散Curvelet变换算法进行指纹图像去噪,克服了传统软、硬阈值去噪的不足之处,不仅使得去噪后的图像边缘纹理细节得到了更好的保持,而且使图像信噪比显著提高约1 dB左右,获得了更好的视觉效果,展现了Curvelet多尺度几何分析工具在指纹图像预处理领域较好的应用前景和极有价值的探索意义。 参考文献: [1] DONOHO D L.Orthonormal Ridgelets and linear singularities[J].SIAM Journal on Mathematical Analysis,1998,31(5):1062-1099. [5] 李 雷.一种基于Curvelet相关图纹理图像检索方法[J].电子技术应用,2016,42(7):119-121. [6] 郝红侠,刘 芳,焦李成.基于Curvelet多方向差和多尺度积的图像去噪[J].华中科技大学学报:自然科学版,2013,41(12):39-43. [7] 何玉杰,李 敏,吕 东,等.一种基于Curvelet变换的红外图像去噪方法[J].计算机工程与应用,2011,47(32):191-193. [8] ZAHRA N, SIDDIQI A H. Denoising of MR images using curvelet transform[J].International Journal of Applied Engineering Research,2015,10(14):34521-34526. [9] STARCK J L, CANDS E J,DONOHO D L. The curvelet transform for image denoising[J].IEEE Transactions on Image Processing,2002,11(6):670-684. [10] 吴芳平,狄红卫.基于Curvelet变换的软硬阈值折衷图像去噪[J].光学技术,2007,33(5):688-690. [11] 柳慧谱,吕 健,潘伟杰,等.基于第二代Curvelet变换的自适应阈值去噪研究[J].微型机与应用,2014,33(10):76-79. [12] 朱 为,李国辉,涂 丹.一种基于第2代曲波变换的尺度相关图像去噪方法[J].中国图象图形学报,2008,13(12):2281-2285. [13] 徐 杰,崔崤峣,向永嘉,等.分布相关的曲波阈值超声图像去噪方法[J].计算机工程与应用,2015,51(19):189-193. [14] KAMBLE V M,PARLEWAR P,KESKAR A G,et al.Performance evaluation of wavelet,ridgelet,curvelet and contourlet transforms based techniques for digital image denoising[J].Artificial Intelligence Review,2016,45(4):509-533. [15] 姚胜南,金 野,唐降龙.基于USFFT Curvelet变换图像去噪算法[J].智能计算机与应用,2011,1(3):17-19. [16] 都伊林,白直灿.第二代曲波变换的图像降噪新算法[J].声学技术,2010,29(3):331-335.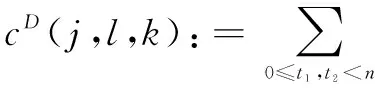
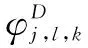
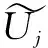
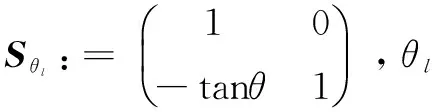
2.3 基于Wrapping的快速离散Curvelet变换实现方法
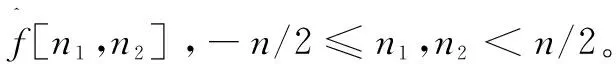
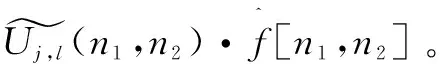
3 基于Curvelet的指纹图像去噪方法
3.1 改进的自适应阈值方案
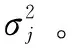
3.2 阈值函数的选择
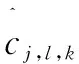
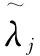
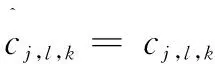
3.3 改进算法步骤
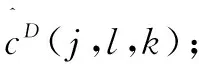
4 实验结果与分析
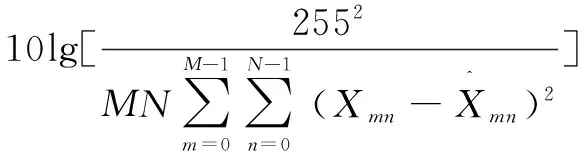
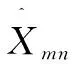
5 结束语

