有源相控阵天线的瞬态热分析方法研究

赵青，胡家渝

（西南电子技术研究所，成都 610036）

热仿真软件已经广泛应用于电子设备热设计中，大大提高了设计的准确性和可靠性。对于有源相控阵天线的热设计，特别是对波长很短的毫米波段，对于其连续波工作状态下的非稳态工作问题，如采用CFD分析，由于时间尺度与空间尺度差距大，将严重增大分析计算量。在空间尺度上，一个MMIC芯片在CFD网格空间分辨率上要求为0.01～0.1 mm之间，而由于天线阵面的其他结构体也要耦合进行计算，导致计算模型的尺度跨度将达到在0.1～1 m左右，甚至更大。巨大的空间尺度差异导致的直接后果是网格层次及复杂度增加，计算的可靠程度降低。在时间尺度上，对于具有不同工作模式的瞬态计算来说，天线各级结构在时间尺度上差距巨大（0.1 ms～10 min），为了捕捉在某些时间间隔之间的芯片温度响应情况，对于时间网格的划分又有严格要求，时间步长必定增加，计算时间将进一步增加，仿真分析软件的实际分析效率将大打折扣。工程中需要一种快速且较为准确的处理方法，对该类问题进行仿真分析。文献[1-4]建立起了器件的DEPHIL模型，但是该模型没有考虑热容，只能用于稳态热分析过程中。文献[5]利用热测试建立了器件的RC模型，并用于板级的热仿真分析，但是其获得需要逐个去实验得到每个器件的RC模型，短期效率比较低，且没有成熟固定的方法或仪器可提供，不便于大规模工程应用。在文献[6-10]中为了修正用于基于故障物理的可靠性仿真模型，使用了红外热像仪对所建立的仿真模型进行验证，文献[11]给出了热耗参数的估算方法。

目前，处理该类问题的主要方法有三类。

1）直接将T/R组件和天线结构体一起详细建模，直接计算，可利用对称边界条件，采用计算1/2天线结构或1/4天线结构的方法。该方法所需网格数量大，计算时间长，对于工程中的大阵面天线，特别是缺乏对称面的天线是不适用的。

2）将T/R组件结构通过测试或仿真分析，抽象出有源RC网络热阻模型，利用该模型，结合天线的其他结构进行与 CFD的联合仿真分析。该方法计算速度块，结果准确，但是对单个多热源组件的模型抽象困难，可能出现多热源热阻网络不可互易等问题。目前对于较为复杂的多热源 T/R组件尚没有一套可行的、成熟的方法与步骤。

3）T/R组件简化计算方法，由于采用方法2）在理论上和技术上存在问题，因此考虑将T/R组件在组件一级上尽量简化、抽象，简化单个组件或通道的芯片数量，从而减少组合后形成的总体模型的计算体量。

1 理论与方法

采用方法3）的核心问题是：判断简化后T/R组件仿真模型的正确性。通常简化T/R组件仿真模型的方法就是减少器件数量，使用虚拟的大面积热源代表离散的有源器件。这是因为热源与天线结构在空间尺度差距最大，热源耗用的网格数多，而减少器件数量可有效降低网格数量，但需要指出在何种情况下使用大面积热源替代是可行的。文中以毫米波T/R组件的空间尺度为例，采用正交分析方法，对比分析了热源器件尺寸参数、安装位置参数与简化的大面积虚拟热源的瞬态响应，给出相关结构、位置参数简化的范围。

以毫米波有源相控阵天线 T/R组件为例，典型T/R组件的有源芯片与T/R腔体之间的几何关系如图1所示。其中K为组件框架1/2边长，W为芯片宽度，L为芯片长度，n为1/2组件芯片个数，芯片厚度统一为 0.1 mm。为了考察各参数对热源简化计算结果的影响，建立一个四因素三水平的正交试验表进行正交试验，以减少试验次数，所采用的正交表见表1。利用该正交试验表对模型进行热仿真分析。

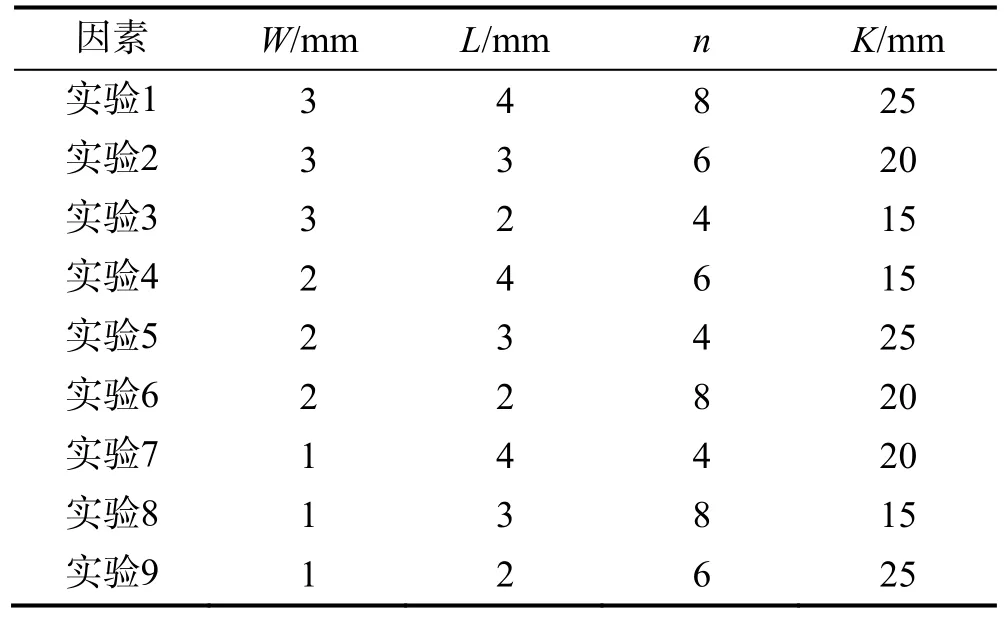
表1 数值实验所用正交实验表

对实验设计的9种模型进行瞬态热分析，分析时间统一规定为150 s，单芯片热耗为0.5 W，记录下芯片安装面监控点的温度tn，使用上述正交试验模型所给的芯片最高温度、最低温度和简化后模型相同监控点的最高温度和最低温度取差值，作为一次数值实验的实验结果，如图2所示。利用极差分析实验结果，所得的各参数对该简化计算误差的贡献如图3所示。可见对简化后计算结果影响最大的是芯片宽度，而最小的因素是芯片个数n。根据试验结果可知，W越宽，简化后的误差越小，W越窄，简化后的误差越大。由于 d=(2K－nW)/n，为方便作为判据用于模型简化，将d/W作为一特征参数，于是，d/W=2K/nW－1。

如图2所示，图中每一个模型都会算出器件的安装面温度tn，而在相同位置点，对于简化的模型同样可算出温度 tn′。将|max(tn)－max(tn′)|作为每次计算试验的实验结果，于是可有如下的各组正交试验结果，见表2。

表2 各监控点最大值为指征的正交实验结果

对各变量进行效应分析，用于给出文中所述类型T/R组件的热源简化，如图4所示。可见当W＞3 mm，K＜20 mm且n＞6时简化前后的的结果偏差趋势相对小，而L对结果的影响是单值的。将实验中的变量参数组合成W/D作为判断标准，并将边界值带入W/D的表达式可知，当W/D＞0.8时，采用这样的简化是合理的。事实上热源所占面积比例越大，和简化假设中的整体平面热源就越一致，当然简化就更为合理。

2 结果及分析

2.1 单个T/R组件的结果验证

利用上述方法与结论，以一个工程中的毫米波相控阵天线T/R组件为例，进行了仿真建模、仿真计算及实验测试。首先按照上述建模流程，考虑主要核心芯片为组件中的功放，将功放、驱动、开关等统一建模为长条状热源，如图5所示。两种不同建模方式计算的表面温度分布云图如图6所示。两种安装面温度随时间变化曲线如图7所示。

同时将 T/R组件在仿真的热耗条件下进行瞬态热测试，实验室内部环境温度为 21.8 ℃，壳体加电后温度为30.5 ℃，工作10 min温度为35 ℃，占空比为5%。实验使用FLUKE TI55红外热成像仪，实验时间为180 s，实验测试结果如图8所示。对比测试结果和仿真分析结果可见，对于详细模型最高温度相差4.5 ℃，对于等效建模组件，温度相差5 ℃。

实验结果表明，对于仿真分析的安装面温度而言，采用简化的单个组件模型和完整建模的单个组件模型计算结果相差为 1.7 ℃，误差小于 5%。将组件的两种仿真模型与实验结果进行对比，非简化模型的误差为10%，简化模型的误差为11%。实验验证结果和所简化的仿真模型结果一致，可用于仿真分析计算。

2.2 整个天线阵面的结果验证

由于阵面较大，不妨采用1/4大小进行计算，所采用的计算域及模型如图9所示。具有详细芯片结构的T/R组件模型，和简化组件的T/R组件模型都进行了仿真分析，以对比计算结果。所用峰值热耗为1361 W（1/4阵面），计算结果如图10—11所示。由于采用了变占空比的热耗，图11中显示的温度随时间变化曲线也随着占空比变化，且两种仿真方式的一致性很好。

计算结果表明，采用验证过的，简化的单个T/R组件模型进行全阵仿真，其计算结果较之详细计算的结果最大误差为 5.1 ℃，最小误差为 1.2 ℃，完全满足工程设计需要。

3 结论

文中采用等效热源的方法简化了单个 T/R组件中分布的芯片，降低了芯片数量，减少了计算网格，有效提高了计算速度。采用正交实验设计的方法进行了数值实验，提出了T/R组件中和组合安装条件下的边界具有一定的等价性。在口径不大的天线毫米波阵面中可以利用这一特性进行模型验证，单个组件的温度响应的实测结果和仿真分析结果误差低于11%，采用详细建模的T/R组件和简化的T/R组件进行天线全阵建模的结果最大误差为5.1 ℃，最小误差为1.2 ℃。计算精度完全满足工程设计需求。

参考文献：

[1] POPPE A, FARKAS G, PARRY J, et al. DELPHI Style Compact Modeling of Stacked Die Packages[C]// 23rdIEEE SEMI-THERM Symposium. 2007.

[2] LASANCE C J M. The European Project PROFIT: Prediction of Temperature Gradients Influencing the Quality of Electronic Products[C], Proc. of the 17thSEMITHERM.2001: 120-125.

[3] RENCZ M, SZÉKELY V, COURTOIS B. A Method for Enerating Dynamic Thermal Multiport Models of Ackages[C]// Inter PACK′01. Kaual, Hawaii, USA, 2001.

[4] SZÉKELY V, PÁHI A, ROSENTAL M, et al. SUNRED:Field Solver and Compact Model Generator Tool Based on Uccessive Mode Reduction[C]// MSM'99. San Juan,Puerto Rico, USA, 1999: 342-345.

[5] RENCZ M. Nclusion of RC Compact Models of Packages into Oard Level Thermal Simulation Tools[C]// IEEE semiconductor Thermal Measurement& Management Symposium. 2005: 71-76.

[6] 张蕊, 汪凯蔚, 沈峥嵘. 高可靠电子设备可靠性仿真试验技术应用研究[J]. 电子产品可靠性与环境试验,2012, 30(6): 13-19.

[7] 李永红, 曾晨晖. 电子产品基于故障物理的可靠性设计优化方法研究[J]. 航空标准化与质量, 2008(4): 39-43.

[8] 陈颖, 高蕾, 康锐. 基于故障物理的电子产品可靠性仿真分析方法[J]. 中国电子科学研究院学报, 2013, 8(5):444-448.

[9] 乔亮, 李传日, 刘龙涛. 基于故障物理的可靠性仿真试验的应用[J]. 装备环境工程, 2012, 9(2): 7-11.

[10] 罗成, 徐文正, 王云, 等. 航空电子产品环境仿真试验技术[J]. 装备环境工程, 2010, 7(6): 21-23.

[11] 朱嘉伟, 李婥, 张铮, 等. 电子装备热仿真关键参数计算方法概述[J]. 电子产品可靠性与环境试验, 2017, 35(4): 62-66.