地下结构抗震设计和分析的反应剪力法

禹海涛

(1.同济大学岩土及地下工程教育部重点实验室,上海 200092; 2.上海市政工程设计研究总院(集团)有限公司,上海 200092;3.同济大学地下建筑与工程系,上海 200092)

0 引 言

近年来,我国城市化发展的进程不断加快,地下空间的开发利用也随之步入了高速发展的阶段,地铁、地下城市综合体等地下结构为我们提供了便利的生活服务。通常认为地下结构处于岩土体介质中,受到岩土体的约束作用,其抗震性能优于地面结构,因此地下结构的抗震问题一直未受到重视。但近年地下结构震害频发,世界各国地震工作者开始重视地下结构的抗震分析。

目前,地下结构抗震分析方法主要有动力时程分析法和拟静力分析法。动力时程分析法作为一种缜密的动力分析手段,通过求解结构的振动微分方程可计算地震动作用时程内任意时刻的结构动力反应,且对于非均质地层有较好的适用性。但动力时程分析法往往需建立二维或三维的地层-结构模型,则边界问题不可避免,同时动力时程分析法计算工作量较大,计算结果处理繁琐,在工程实践应用中效率较低。拟静力分析法是将动力学问题转化为静力学问题的简化方法,该方法能较好地反映结构的动力反应,具有计算结果直观、计算效率高等优点,在工程实践中得到广泛应用。地下结构抗震分析的拟静力方法较多,如20世纪初,日本学者大森房吉最早提出静力理论指导隧道抗震设计;20世纪60年代,美国旧金山修建快速地铁时提出了BART法[1];Shukla基于弹性地基梁理论提出了Shukla法[2];前苏联学者提出了基于连续介质弹性力学的福季耶娃法[3];其中日本于20世纪70年代提出的反应位移法应用最为广泛。目前,国家规范《城市轨道交通结构抗震设计规范》(GB 50909—2014)[4]和上海市地方规范《地下铁道建筑结构抗震设计规范》(DG/TJ08-2064—2009)[5]均推荐反应位移法作为地下结构抗震设计方法。

近年反应位移法在抗震分析中得到了广泛的应用,但其在计算地下结构地震反应时精度不高,且存在非均质地层适用性较差、离散地基弹簧难以真实模拟土结相互作用、参数选取不明确等诸多问题。本文对反应位移法进行了深入研究,分析了反应位移法的不足及其原因;同时,在反应位移法的基础上,提出一种基于地层-结构模型的反应剪力法,并评价了其对不同场地条件和不同结构断面形式的适用性。

1 反应位移法的不足

拟静力分析法是将随时间变化的地震作用转化为等效静荷载或者等效静位移,通过静力分析计算结构在地震荷载下的附加内力及变形。反应位移法作为经典的拟静力分析法,其主要思想为:地下结构的地震动反应主要由其周围土层运动控制,把周围土体看作支撑结构的地基弹簧,将周围土体在地震作用下产生的位移通过地基弹簧以静荷载的形式施加给结构,分析结构的地震附加内力(下文均简称内力)和变形[6]。反应位移法假定:①结构与土体均为各向同性的线弹性体;②忽略土体之间的相互影响[7]。

采用反应位移法进行地下结构横断面的抗震分析时,将地震作用等效为三种静荷载:结构位置处土层的相对位移、地层剪力、结构自身惯性力。对于圆形隧道结构,其计算模型如图1所示。研究表明[8],土层相对位移和地层剪力是影响结构反应的主要因素,而结构自身惯性力的影响较小,计算时可忽略。关于地层位移的确定,规范[4]建议采用一维土层地震反应分析程序(SHAKE91[9]等)或反应谱法计算土层相对位移,然后将土层相对位移施加在地层弹簧上。

反应位移法作为目前规范推荐的地下结构抗震设计方法,在工程实践中广泛应用。但其在实际工程应用中仍存在诸多问题[10-11]:

(1) 反应位移法对于非均质地层的适用性较差。

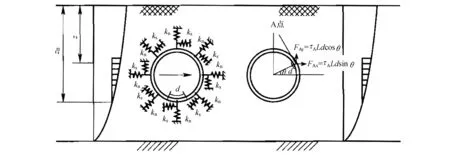
图1 反应位移法隧道横断面计算模型[4]Fig.1 Simplified model for tunnel cross section calculation using the response displacement method[4]

(2) 为获得较精确的地基弹簧刚度,需建立地层模型,利用静力有限元进行多次计算,工作量较大。

(3) 对于断面形式复杂的结构,地层剪力的施加较困难。

(4) 我国缺乏场地速度反应谱相关资料,无法采用速度反应谱确定地层强制位移,而必须依靠一维土层地震反应分析程序确定地层强制位移,操作较繁琐。

以上因素一定程度上制约了反应位移法在地下结构抗震分析中的推广应用。

针对反应位移法的诸多问题,国内外学者提出了多种基于反应位移法的优化方法,如日本学者片山幾夫等[12]提出的反应加速度法;何川等[13]提出的广义反应位移法;刘如山[10]提出的反应应力法;刘晶波[11,14]提出的整体式反应位移法和地下结构Pushover 分析方法,这些学者的研究一定程度上改善了反应位移法的适用性。

本文基于反应位移法基本原理,提出了一种基于地层-结构模型的反应剪力法。相比反应位移法,该方法具有更好的地层条件适用性及计算操作简便性。

2 反应剪力法的提出

研究表明[11],反应位移法的诸多不足主要源自于地基弹簧。反应位移法在结构模型中设置离散弹簧模拟土-结构相互作用,忽略土体之间的相互作用,同时离散地基弹簧难以真实模拟土体与结构间连续接触面的相互作用,因此导致反应位移法在实际工程应用中产生较大的误差。为克服反应位移法的不足,本文舍弃反应位移法中的梁-弹簧模型,建立地层-结构模型以更真实地模拟土-结构相互作用。考虑到结构横断面的尺寸远小于地震波波长,在水平横向地震作用下,土体与结构间的相互作用可近似为均匀剪切作用[15],从而提出了基于地层-结构模型的反应剪力法。

2.1 基本思想

反应剪力法基于反应位移法的基本原理,由土体自由场的地震反应分析,得到天然地层的应力状态如图3(a)所示,取出结构所在位置的土体单元,简称为等代土体单元。通常地下结构高度相对较小,等代土体单元上下表面的地层剪力τ1、τ2相差不大,为便于分析,可做简化处理[16],取其上下表面地层剪力的平均值τ近似代替τ1、τ2,其中:

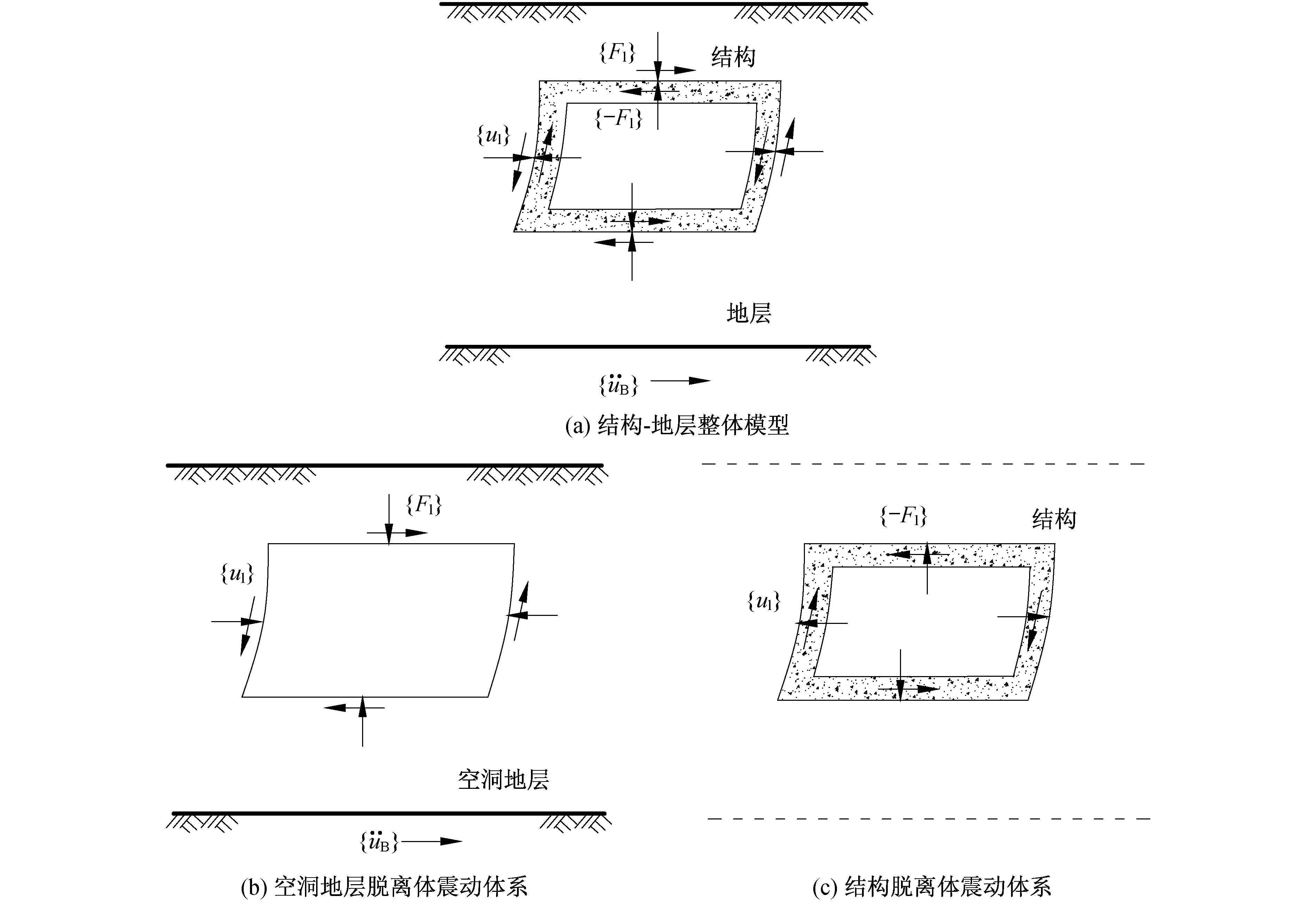
图2 结构-地层脱离体Fig.2 The detached parts of soil-structure systemτ=(τ1+τ2)/2

(1)

因此,等代土体单元简化后的应力状态如图3(b)所示,四周受均布地层剪力τ作用,同时产生地层剪切位移δ:

(2)

式中：H为等代土体单元的高度(m);γ为等代土体单元的剪应变;G为土体的剪切模量(Pa)。

以等代土体单元形心为中心向四周边界扩充其地层范围,得到一个与等代土体单元几何相似的地层模型,称之为等代地层模型,等代地层模型的四周边界同样施加同等的均布剪力τ,如图3(c)所示。由弹性力学基本知识可知,图3(b)与图3(c)所示模型的土体应力状态相同,等代地层模型中的等代土体单元的剪应变仍为γ,即扩充地层范围不改变等代土体单元的应力状态。故对于等代土体单元而言,等代地层模型边界上的均布剪力τ(图3(c))可等效代替地震荷载。为模拟反应位移法中结构脱离体与空洞脱离体间的相互作用,取出等代地层模型中的等代土体单元,将结构脱离体放入其空洞,如图3(d)所示,此时均布剪力τ可作为地下结构的等效地震荷载。通过设置合理接触,将等效地震荷载施加在地下结构上,从而求解地下结构的地震反应。

反应剪力法利用等代地层模型模拟空洞地层,用地层剪力代替地震荷载,将空洞与结构脱离体重新结合,不仅可以真实模拟土体与结构间连续接触面的相互作用,同时反应剪力法不直接施加土体自由场相对位移,可充分考虑结构对地层变形的影响,从而较真实地反映结构的地震反应。

2.2 地震引起的等效地层剪应力

地震作用下地层发生剪切变形,并产生地层剪应力,结构顶底点产生最大相对位移差时,地层处于最大剪应变状态,可认为此时地下结构受到的地震荷载最大,对结构也最不利。因此,可将此刻对应的最大地层剪力定义为等效地层剪应力,通常结构顶底点的地层剪力相差不大,地震引起的等效地层剪力可取结构顶底点剪力的平均值[16]:

(3)

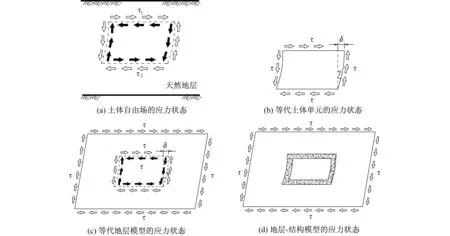
图3 反应剪力法中空洞地层等效Fig.3 The equivalent model of opening hole in free field using the response shear stress method

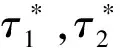
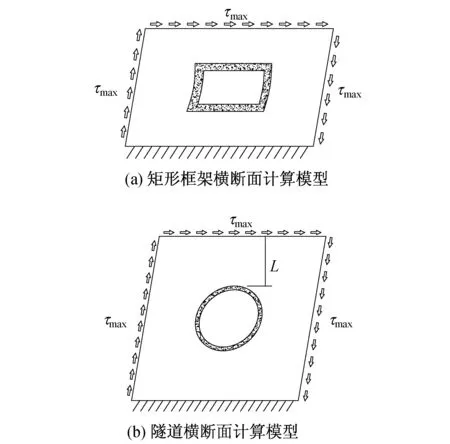
图4 反应剪力法的地层-结构计算模型Fig.4 Simplified soil-structure model for response shear stress method

2.3 反应剪力法计算流程

综合上述分析,本文所提出的反应剪力法具体计算步骤如下:

(1) 求解等效地层剪应力。建立土层自由场模型,采用一维土层地震反应分析程序(SHAKE91等)求解土体自由场地震反应,取最大相对位移时刻对应结构顶、底点深度处的地层剪力平均值作为等效地层剪应力τmax。

(2) 建立地层-结构有限元模型。利用有限元程序建立如图4所示的有限元模型(模型的边界尺寸要求见第3.4节详述),地层与结构间的接触可以考虑滑移或不滑移,约束模型底部的竖向和水平向位移。

(3) 进行拟静力计算。将第一步计算所得等效地层剪应力τmax施加在地层-结构有限元模型的顶面和侧面边界上,通过静力计算,得出结构的地震反应。

3 反应剪力法对于盾构隧道的适用性评价

对于地层-结构模型,地层模型边界的选取对计算精度影响较大。对于圆形盾构隧道,地层模型边界如图4(b)所示,各侧边界到隧道结构的距离均为L。以动力时程分析法为基准,采用反应剪力法进行不同模型边界尺寸的参数化分析,以内力计算误差为评价指标,确定L的最优化取值,同时对比反应位移法与反应剪力法的计算精度,评价反应剪力法对于不同软土地层条件下盾构隧道的适用性。

3.1 模型参数

依托典型的地铁区间盾构隧道,隧道直径D=6 m,衬砌壁厚t=0.35 m,隧道中心埋深为15 m。混凝土重度为25 kN/m3,弹性模量为34.5 GPa,泊松比为0.2。为便于计算,隧道结构简化为均质圆环。

为使地层模型边界尺寸更具一般性,土体选用不同的地层参数。考虑到区间隧道所处地层的剪切波速通常在100 m/s～400 m/s,假定为均质土进行分析。为考虑土体动力非线性[17],即土体的动剪切模量随剪应变增大而衰减,采用一维土层地震反应分析程序SHAKE91计算对应地震水准下的土体等效动剪切模量G,进而得到土体的等效动弹性模量E,具体地层参数见表1。

表1 地层参数Table 1 Ground parameters

为保持输入地震动的一致性,各种分析方法均从距地表70 m的基底处输入El Centro波,其加速度时程曲线如图5所示。

3.2 动力时程分析模型

本文以动力时程分析结果为基准,评价反应剪力法的计算精度。基于ABAQUS有限元程序建立动力时程分析模型,采用平面应变单元模拟隧道周围土体,采用二维梁单元模拟隧道结构。土体侧面采用自由边界,为避免边界效应的影响,土体两侧边界距隧道结构取为隧道直径的50倍,如图6所示。假设隧道结构与土体不发生相对滑移,且土体与结构均采用线弹性模型。

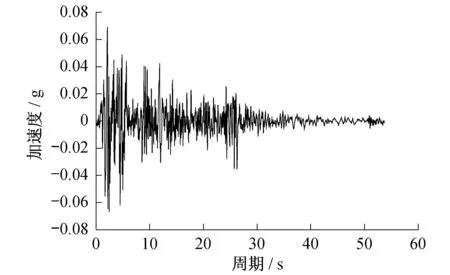
图5 El-Centro地震波Fig.5 El-Centro seismic wave

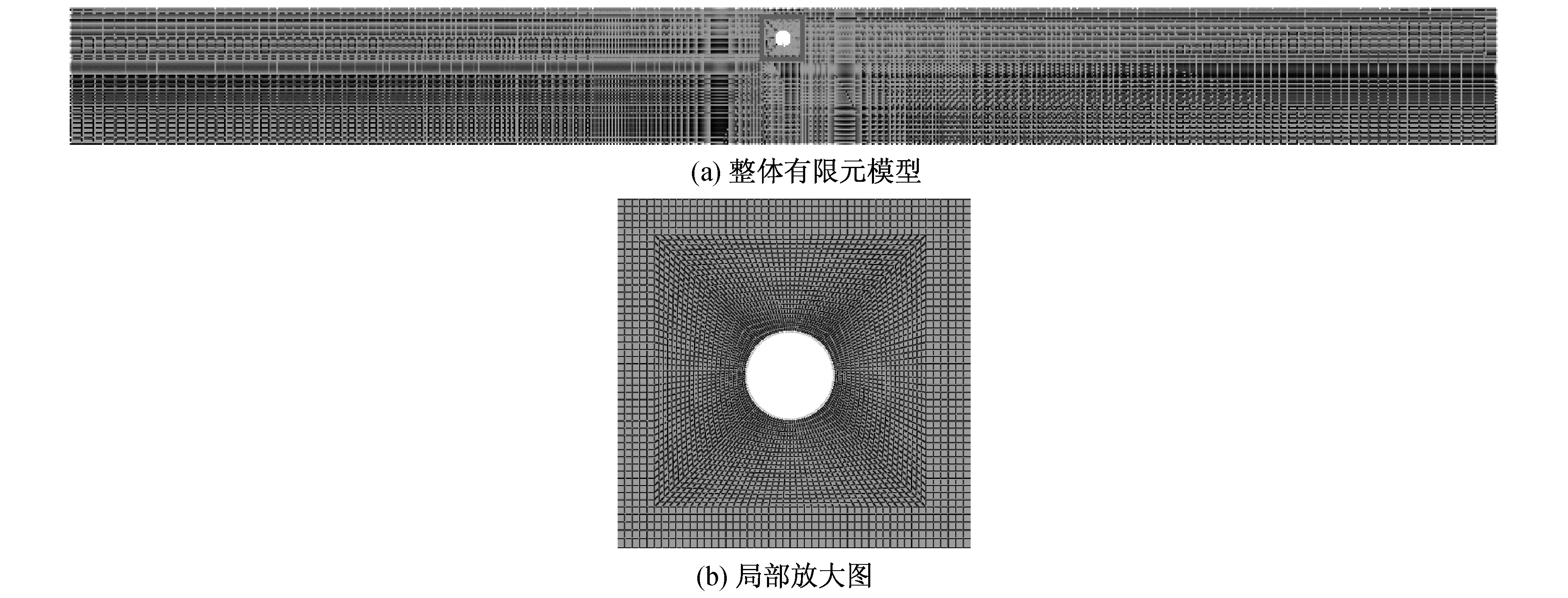
图6 动力时程有限元模型Fig.6 Finite element model of the dynamic time-history analysis method

土体采用Rayleigh阻尼理论模型,Rayleigh阻尼模型是广泛采用的一种正交阻尼模型,其数学表达式如下:

C=αM+βK

(4)

式中：α为质量阻尼比例常数;M为质量矩阵;β为刚度阻尼比例常数;K为刚度矩阵。

α和β可由式(5)确定:

(5)

式中：ξn第n阶振型的模态阻尼比;ωn为第n阶振型频率。

通常由前两阶模态确定α和β,利用ABAQUS软件进行土体自由场模态分析得到ω1、ω2,取ξ1=ξ2=0.05,由式(5)求解α、β。

3.3 反应位移法与反应剪力法模型

反应位移法与反应剪力法的计算模型及参数与动力时程分析方法保持一致。利用SHAKE91程序求解土体自由场的地震反应,将相应的地层剪力、土层相对位移、结构惯性力施加于反应位移法模型,如图7(a)所示;将相应的等效地层剪力施加于反应剪力法模型,如图7(b)所示,分别采用两种拟静力方法求解结构地震反应。

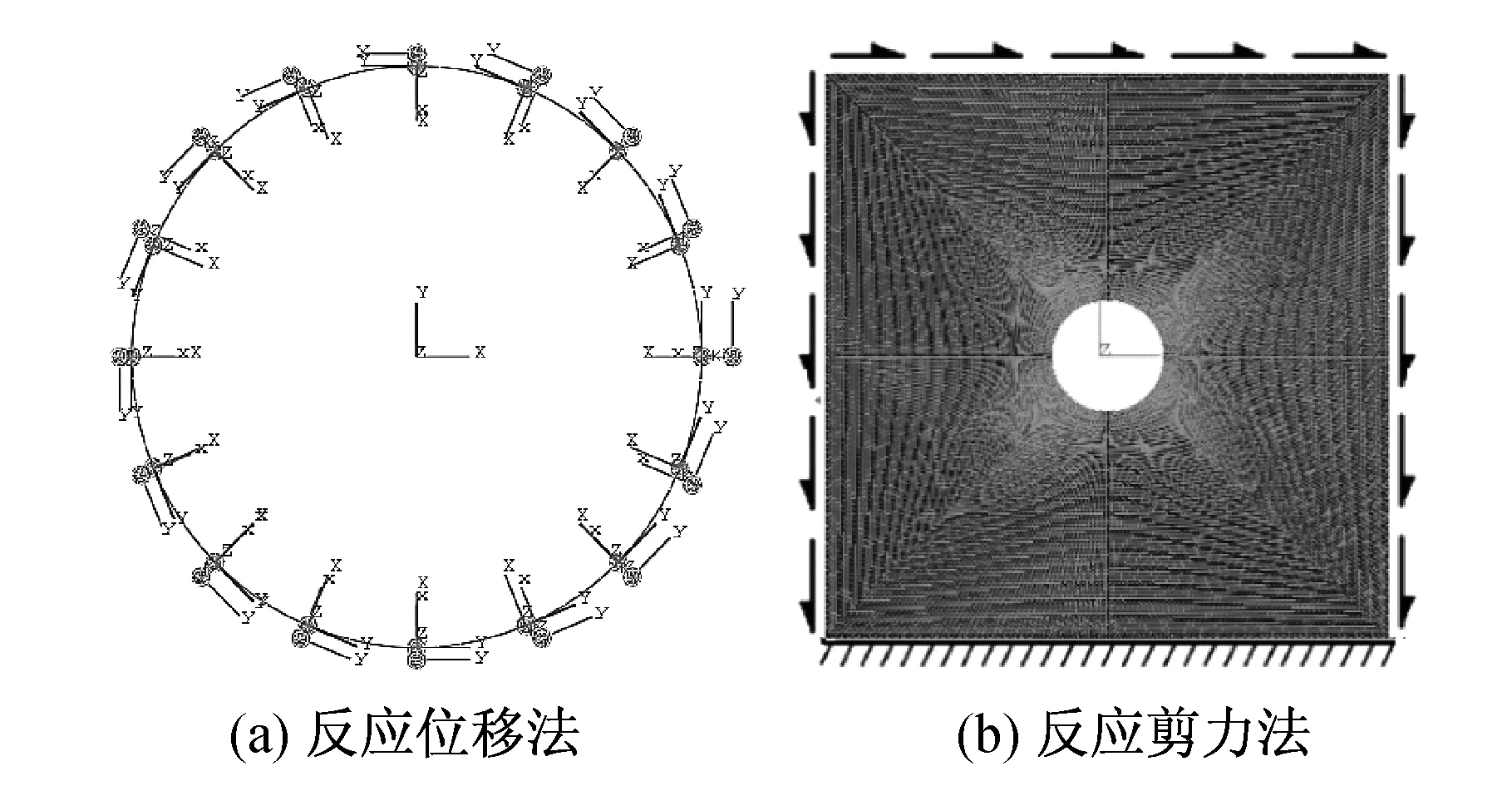
图7 拟静力方法有限元模型Fig.7 Finite element models of the quasi-static method

3.4 反应剪力法地层模型边界尺寸的确定

通过比较反应剪力法不同地层模型边界尺寸对应的内力相对误差,确定合理的地层模型边界尺寸L。取隧道顶底点发生最大相对位移时刻的结构内力为评价指标。隧道结构在地震作用下,动力时程法与反应剪力法计算得到的最大轴力及最大弯矩均发生在隧道横断面斜向45°处,最大剪力出现在隧道横断面的顶底点处,呈对称分布,故以此作为内力观察点。

定义内力相对误差:

(6)

式中：FS为反应剪力法的计算结果;FT为动力时程法的计算结果。

由图8可知,当地层模型边界尺寸L≥5D时,内力相对误差趋于稳定,故地层模型边界尺寸L可取5倍的隧道直径。

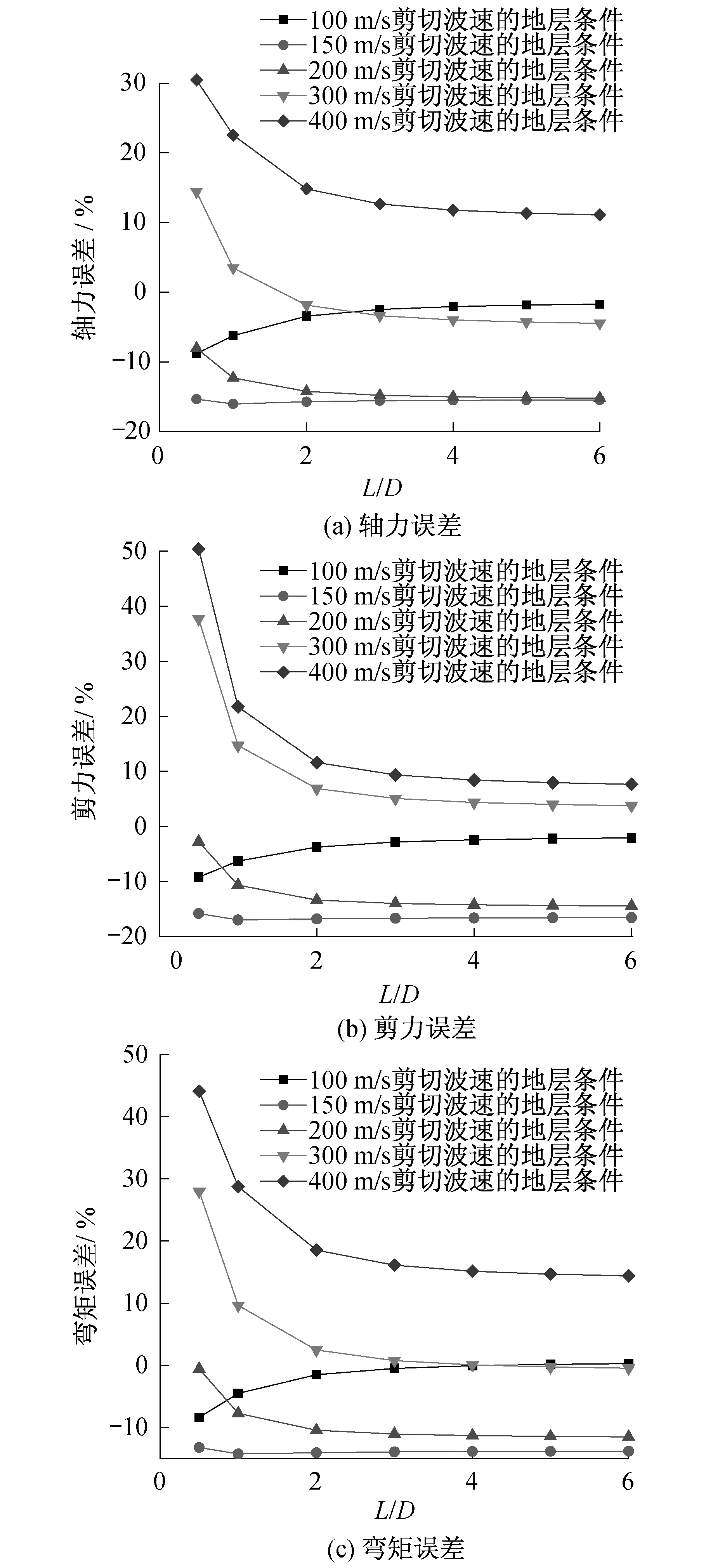
图8 截面内力误差分析Fig.8 Errors analysis of internal forces in tunnel section

3.5 对比分析与评价

以动力时程法为基准,对比分析反应位移法与反应剪力法对于圆形隧道的适用性。反应剪力法选取地层模型边界尺寸L=5D的计算结果。内力提取点见3.4节,得到地震作用下隧道的最大内力如表2所示。

由表2中动力时程法分析结果可知,随地层剪切波速的增大,结构的轴力逐渐增大,剪力与弯矩先增大后减小。对比两种拟静力方法的内力误差可以看出,反应位移法的计算误差明显偏大,尤其结构轴力,其相对误差最大超过了50%;相比之下,反应剪力法的计算精度较高,内力最大相对误差可控制在15%左右。由此可知,反应剪力法的计算精度明显优于反应位移法,且在各种地层条件下均有较好的适用性。

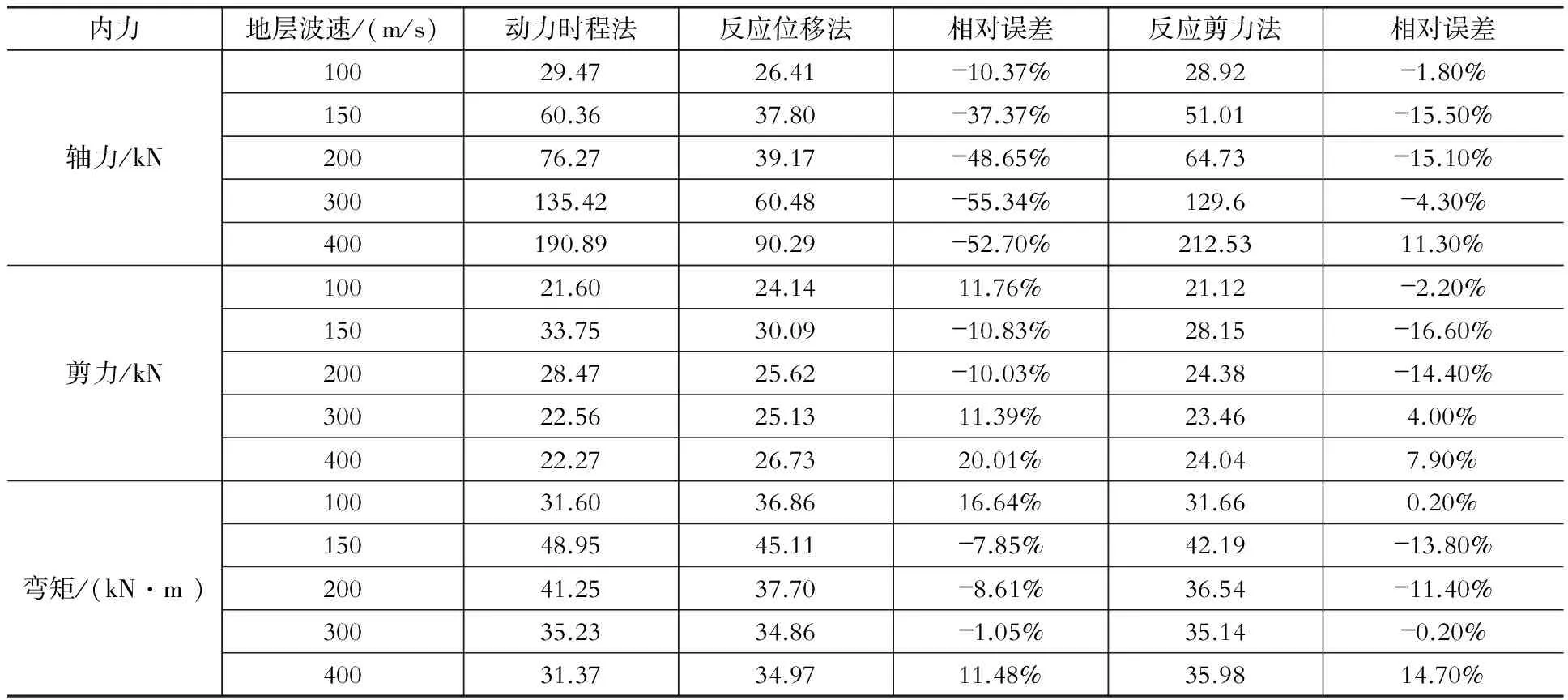
表2 不同方法截面内力误差Table 2 Sectional force errors of different methods

4 反应剪力法对于矿山法隧道的适用性评价

相比圆形隧道,断面形状不规则的矿山法隧道采用反应位移法进行抗震分析时,操作更加繁琐,由于其每段圆弧的圆心不同,致使地基弹簧方向的设定、地层剪力的计算与施加等操作存在困难。反应剪力法由于基于地层-结构模型,分析中将不受结构截面形式的限制,对于横断面形状不规则的结构有明显优势。现以典型的马蹄形矿山法隧道为例,评价反应剪力法对于不同围岩条件下矿山法隧道的适用性。

4.1 计算模型

隧道中心埋深30 m,横断面如图9所示,衬砌厚0.5 m,衬砌材料参数与第三节盾构隧道保持一致。为探究反应剪力法对于矿山法隧道的普遍适用性,地层选用不同的围岩参数。考虑到矿山法隧道所处围岩的剪切波速通常在500 m/s～3 000 m/s,故以此范围假定为均质围岩进行分析。围岩采用等效动弹性模量,具体围岩参数见表3。基于模型边界尺寸的参数化分析,竖向、水平向地层模型边界分别取隧道高度、宽度的5倍,建立如图10所示的有限元模型。假设隧道结构与土体不发生相对滑移,且隧道及围岩均采用线弹性模型。动力时程分析模型的参数选取与盾构隧道算例保持一致。

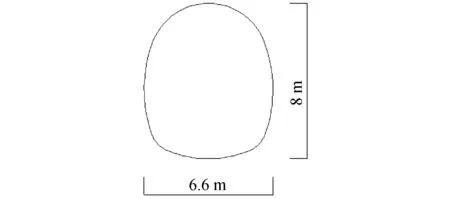
图9 矿山法隧道横断面Fig.9 The cross section of tunnels constructed by mining method

4.2 结果分析

以动力时程法为基准,分析反应剪力法对于不同围岩条件下矿山法隧道的适用性。基于结果分析,矿山法隧道在地震作用下最大内力均发生在拱脚处,故提取拱脚处的最大内力作为评价指标,如表4所示。

图10 矿山法隧道有限元模型Fig.10 Finite element model of tunnels constructed by mining method

由表4可知,随围岩剪切波速的增大,结构的内力逐渐变小。对比两种分析方法的内力数值,反应剪力法的内力结果与动力时程法基本一致,当围岩波速v=2 500 m/s时,反应剪力法的计算误差最大,但最大误差仅为10%左右。此外,内力误差大小与围岩波速无明显的相关性,说明反应剪力法的计算精度不会受岩体剪切波速的影响。为进一步验证反应剪力法的有效性,绘制围岩波速v=2 500 m/s工况下两种方法的结构内力图,见图11。由图可见两种方法的内力图几乎完全重合,内力分布及数值均完全一致。综上所述,反应剪力法在各种围岩条件下的计算精度均较高,可真实地反映结构在地震作用下的内力反应。

表3 围岩参数Table 3 Surrounding rock parameters

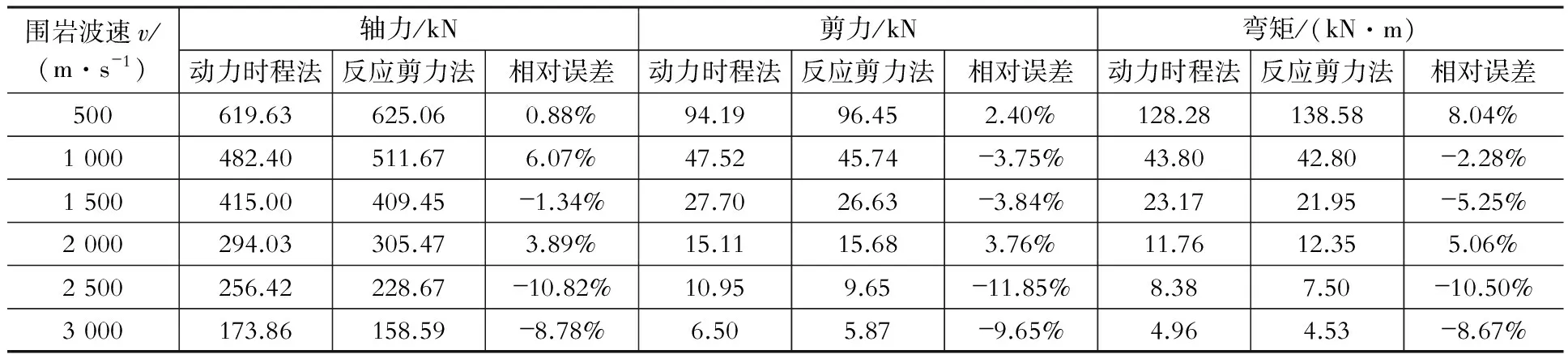
表4 反应剪力法截面内力误差Table 4Sectional force errors of response shear stress method

5 结 论

本文在反应位移法的基础上,提出一种基于地层-结构模型的反应剪力法。其主要思想为:水平横向地震作用下土体与结构间多为均匀剪切作用,可将最不利的地层剪应力定义为等效地层剪应力,基于一维土层地震反应分析程序计算该等效地层剪应力,将其施加在地层-结构模型上,通过静力计算求解结构地震反应。以动力时程方法为基准,通过系列算例分析,评价了反应剪力法对于不同地层条件和不同结构形式的适用性,结论如下:

(1) 基于地层-结构模型的反应剪力法可真实反映土体与结构间连续接触面的相互作用,且无需计算繁琐的地基弹簧刚度,分析流程更为简便。

(2) 反应剪力法由一维土层地震反应分析程序SHAKE91求解土体自由场地震反应,确定等效地层剪应力,既可考虑土体的动力非线性,又避免了动力时程分析模型的边界问题,具有较高的计算精度。

(3) 通过参数化分析,确定反应剪力法的模型边界尺寸取为结构尺寸的5倍即可获得较好的计算精度。

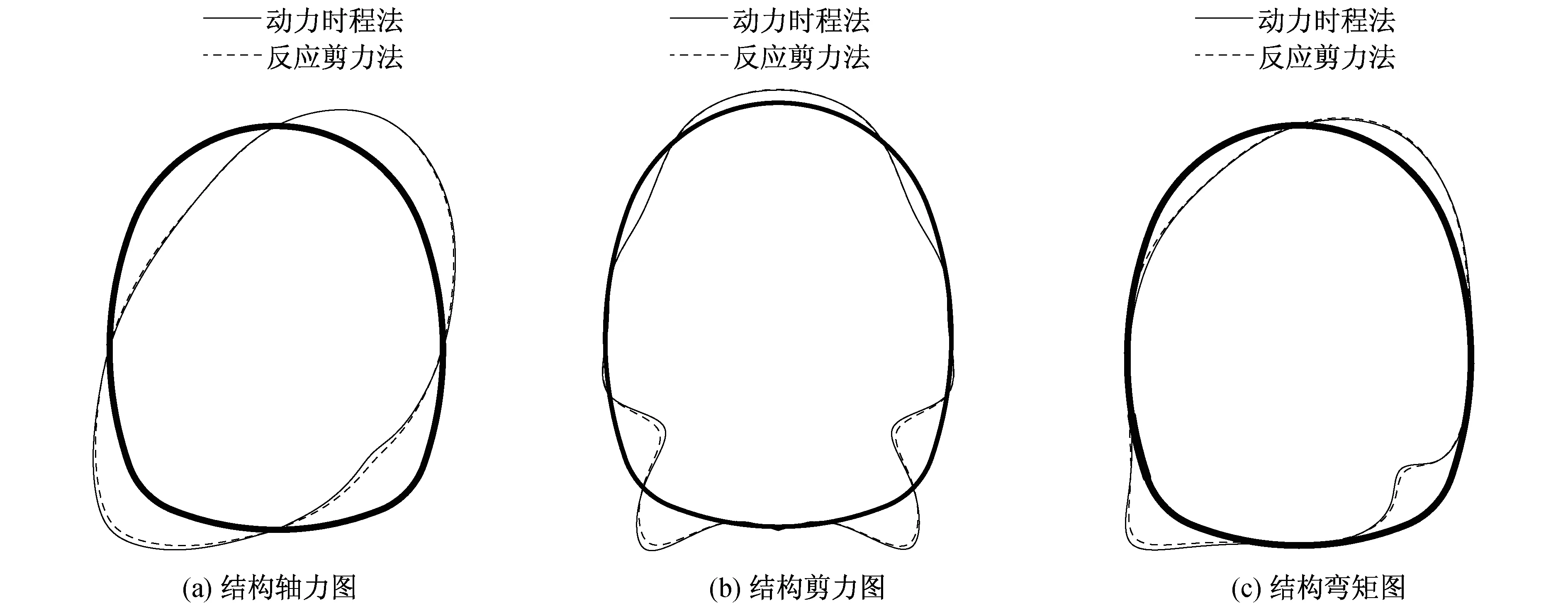
图11 不同方法的内力图(围岩波速v=2 500 m/s)Fig.11 Internal force diagram of different methods (v=2 500 m/s)

(4) 反应剪力法在不同场地条件、不同结构断面形式下的计算结果均与动力时程分析法保持一致,而反应位移法的计算误差均较大。

(5) 相比反应位移法,反应剪力法具有更广泛的场地条件和结构形式适用性,参数确定简单,在保证较高计算精度的同时大幅提高了计算效率。

参考文献

[1] Kuesel T R.Earthquake design criteria for subways[C].Journal of the Structural Division Proceedings of the American Society of Civil Engineers,1969,(6) :1213-1231.

[2] Shake D K,Rizzo P C,Stephenson D E.Earthquake load analysis of tunnels and shafts[C].Proceedings of the 7th World Conference on Earthquake Engineering.Michigan:University of Michigan Press,1980:20-28.

[3] 福季耶娃.地震区地下结构支护的计算[M].徐显毅,译.北京:煤炭工业出版社,1986.

Fotieva.Calculation to the support of underground structures in seismic region[M].Xu Xianyi,trans.Beijing:China Coal Industry Publishing House,1986.(in Chinese)

[4] 中华人民共和国国家标准编写组.GB 50909—2014城市轨道交通结构抗震设计规范 [S].北京:中国建筑工业出版社,2014.

The National Standards Compilation Group of People’s Republic of China.GB 50909—2014 Code for seismic design of urban rail transitstructures [S].Beijing:China Architecture and Building Press,2014.(in Chinese)

[5] 中华人民共和国国家标准编写组.DG/TJ 08—2009 地下铁道建筑结构抗震设计规范[S].上海:[s.n.],2009.

The Professional Standards Compilation Group of People’ Republic of China.DG/TJ08—2009 Code for seismic design of subway structures[S].Shanghai:[s.n.],2009.(in Chinese)

[6] 袁勇,禹海涛,陈之毅.软土浅埋框架结构抗震计算方法评价[J].振动与冲击,2009,28(8):50-56.

Yuan Yong,Yu Haitao,Chen Zhiyi.Evaluation of seismic calculation methods for shallow-buried frame structures in soft soil[J].Journal of Vibration and Shock,2009,28(8) :50-56.(in Chinese)

[7] 禹海涛,袁勇 ,张中杰 ,等 .反应位移法在复杂地下结构抗震中的应用[J].地下空间与工程学报,2011,05:857-862.

Yu Haitao,Yuan Yong,Zhang Zhongjie,et al.Application of response displacement method on seismic design of a complex underground structure[J].Chinese Journal of Underground Space and Engineering,2011,05:857-862.(in Chinese)

[8] 川岛一彦.地下构筑物の耐震设计[M].日本:鹿岛出版会,1994.

Kawajima K.Aseismic design of underground structure[M].Japan:Kajima Institute Publishing Co.,Ltd.1994.(in Japanese)

[9] Idriss I M ,Sun J.User’s manual for SHAKE91 A computer program for conducting equivalent linear seismic response analyses of horizontally layered soil deposits center for geotechnical modeling[R] .Department of Civil & Environmental Engineering,University of California,Davis,California,August1992.

[10] 刘如山,胡少卿,石宏彬.地下结构抗震计算中拟静力法的地震荷载施加方法研究[J].岩土工程学报,2007,29(2):237-242.

Liu Rushan,Hu Shaoqing,Shi Hongbin.Study on seismic loading of pseudo-static approach used in the seismic design of underground structure[J].Chinese Journal of Geotechnical Engineering,2007,29(2) :237-242.(in Chinese)

[11] 刘晶波,王文晖,赵冬冬,等.地下结构抗震分析的整体式反应位移法[J].岩石力学与工程学报,2013,32(8):1618-1624.

Liu Jingbo,Wang Wenhui,Zhao Dongdong,et al.Integral response deformation method for seismic analysis of underground structure[J].Chinese Journal of Rock Mechanics and Engineering,2013,32(8):1618-1624.(in Chinese)

[12] 片山幾夫,足立正信,嶋田穣,等.地下埋設構造物の実用な準動的解析法「応答震度法」の提案[C].土木学会.土木学会第40回年次学術講演会講演概要集第1部門.东京:土木学会,1985:1-9.

[13] He C,Koizumi A.Study on seismic behavior and seismic design methods in transverse direction of shield tunnels[J].Structural Engineer and Mechanics,2001,11(6):651-662.

[14] 刘晶波,刘祥庆,李彬.地下结构抗震分析与设计的Pushover 分析方法[J].土木工程学报,2008,41(4):73-80.

Liu Jingbo,Liu Xiangqing,Li Bin.A pushover analysis method for seismic analysis and design of underground structures[J].China Civil Engineering Journal,2008,41(4):73-80.(in Chinese)

[15] Penzien J.Seismically induced cracking of tunnel linings[J].Earthquake Engineering and Structural Dynamics,2000,29:683-691.

[16] 晏启祥,马婷婷,吴林,等.反应位移法在盾构隧道横向抗震分析中的应用[J].铁道建筑,2010,09:48-51.

Yan Qixiang,Ma Tingting,Wu Lin,et al.Application of the response displacement method to the aseismic design for cross-section of shield tunnel[J].Railway Engineering,2010,09:48-51.(in Chinese)

[17] 周川,焦玉勇,张国华,等.等效线性方法在地铁车站抗震分析中的应用[J].地下空间与工程学报,2015,S2:518-525.

Zhou Chuan,Jiao Yuyong,Zhang Guohua,et al.Application of equivalent linear method in the subway station seismic analysis[J].Chinese Journal of Underground Space and Engineering,2015,S2:518-525.(in Chinese)