BUCK/BOOST直流变换器的建模仿真验证

王 钊，马丛淦，宋振辉

(国网北京市电力公司，北京 100031)

0 引言

直流变换器可以对直流电压进行变换，通常被称作二次电源。降压变换器(BUCK变换器)和升压变换器(BOOST变换器)是2种最基本的直流/直流电压变换器，相关元件在电力仿真中有广泛的应用。

下面主要介绍这2种直流变换器的电路结构与工作原理，并通过OrCADPspice电路仿真软件进行建模与仿真验证，相关方法可为实际电力系统中直流/直流变换、交/直/交变换元件仿真提供依据和参考。

1 BUCK变换器

1.1 电路结构与原理

图1是BUCK变换器的电路原理图。开关T和二极管D构成了最基本的开关型直流/直流降压变换电路。通过对开关进行周期性的通断控制，可以将直流电源的输入电压VS变换为电压Vo，输出给负载。

图1 BUCK变换器的电路结构

在开关导通的Ton=DTS期间，直流电源VS经开关直接输出，二极管承受反向电压而截止，流经二极管的电流iD=0，电源电流iS经开关T流入电感负载，电感电流iL逐渐上升至iS，变换器的输出电压VEO=VS。电感负载两端的电压存在如下关系：

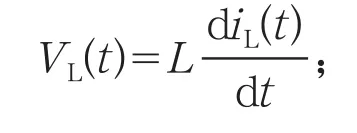
在开关T阻断的Toff=(1-D)TS期间，电路的负载与电源脱离。由于电感电流iL并不能立即降为0，期间iL经负载和二极管续流，二极管也因此被称作续流二极管。

在整个开关阻断的Toff期间，电感电流iL经二极管环流，若阻断时间足够短，则二极管一直处于导通状态。

整个周期中输出电压的直流平均值为：

1.2 仿真建模与验证分析

图2为依据图1的电路原理，通过OrCADPspice电路仿真软件，对BUCK变换器进行的仿真模拟。图1中的控制开关通过场效应管（MOSFET）实现。将电压探头放置在对应位置，即可测量变换器的输出电压。在OrCADPspice仿真软件中，可以变更导通比、开关频率等参量，并在同一幅图像中显示不同参量对应的输出电压波形曲线，观察参量变化对输出电压造成的影响。

为了验证降压变换器的输出电压与导通比的关系，将导通比设置为0.1，0.2，……，0.9这9个数值，观察电压波形曲线的变化关系，如图3所示。从图3显示的波形曲线中可以清晰地发现，当输出电压值趋于稳定(t=3.0ms)之后，电压值与导通比呈正比关系。线路通电后，由于电感电流需要一段时间才能增加到iS，该过程对应图3中t=3ms之前的充电期。

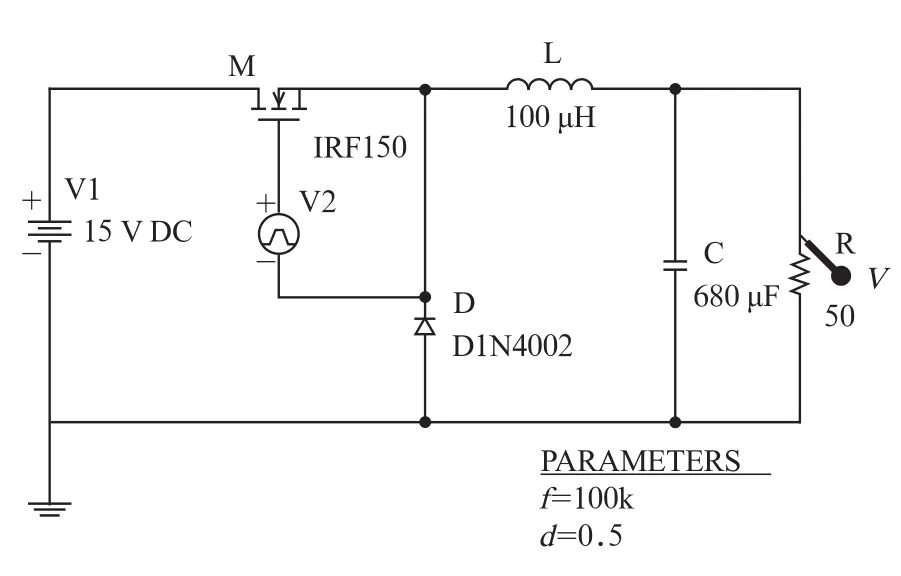
图2 降压变换器的仿真拓扑结构

图3 不同导通比状态下对应的输出电压波形

同样的方法还可以观察不同的开关频率对输出电压造成的影响。将fS设置为 40kHz，60kHz，80kHz和 100kHz这 4 个等级，观察不同频率对应的电压波形，如图4所示。

图4是在开关导通比不变的前提下(设D=0.5)，对应4个不同开关频率状态下的4条输出电压曲线。可以发现，变换器的输出电压随着开关频率变化，也发生微小的变化。随着开关频率增大，输出电压值略微下降。图5是图4中9.90—10.10ms时间段的区段放大的电压曲线。

(三)奢泰。奢即是奢侈，泰即是过度，奢泰就是违背自然规律而走向极端过分的主观行为。老子是辩证法大师，他看到了“物极必反”、“物壮则老”的基本规律，“物壮则老，是谓不道，不道早已”(三十章)。[3]“反者道之动，弱者道之用”(四十章)。[3]他主张适度原则，不搞极端，不搞过分，不搞奢侈，希望人们从圣人的思想中去体会立身处世的原理，做到“去甚、去奢、去泰”(二十九章)。[3]违反适度原则而走向奢泰，就会出现危险。如物质生活的过度，就会出现“五色令人目盲，五音令人耳聋，五味令人口爽”(十二章)[3]的结局。

当电压趋于稳定后，图3—5的电压波形曲线趋于一条直线，但将坐标轴放大，会清晰地发现电压波形实际为正弦曲线，图3—5的直线反映了输出电压平均值。图6显示的是将坐标轴适当放大之后的输出电压波形(以图5中80kHz的开关频率为例)。若将图3—5的其他波形曲线按照相应比例放大，同样也能观察其波形变动情况。

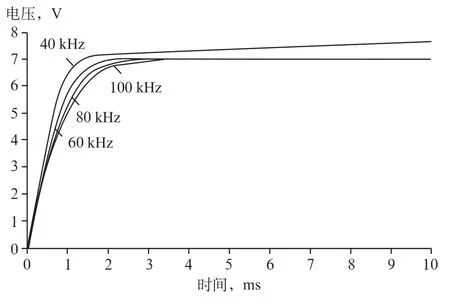
图4 不同开关频率对应的输出电压波形曲线

图5 不同开关频率对应的输出电压波形曲线(区段放大)

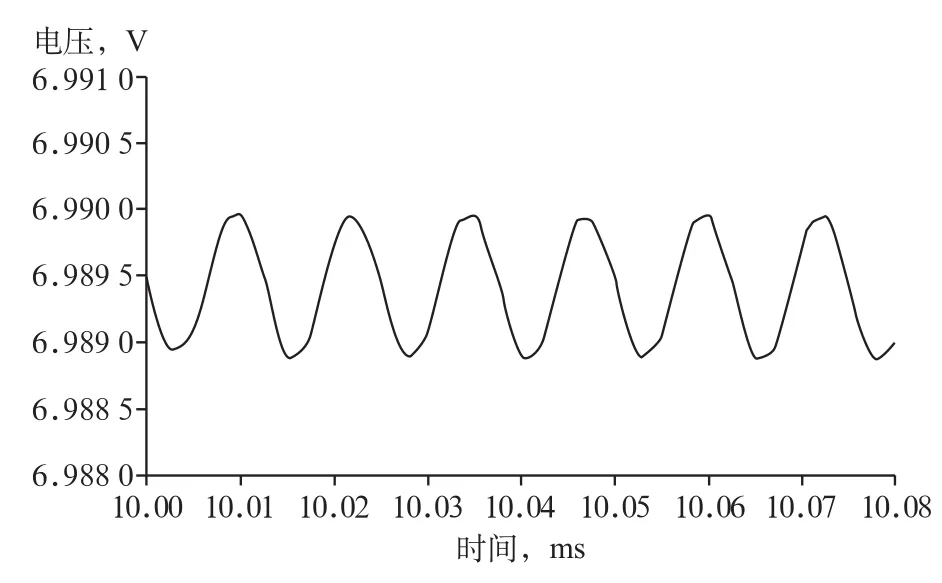
图6 80 kHz输出电压波形曲线

将电压和电流探头放在BUCK变换器对应的位置，就可以得到图1中电感L和电容C的两端电压和流入电流波形曲线，如图7和8所示。

2 BOOST变换器

2.1 电路结构与原理

图9是BOOST变换器的电路原理图。

为了获得高于电源电压VS的直流输出电压Vo，在BOOST变换器开关前段插入电感L，在开关T阻断时，利用电感线圈L在电流变小过程中产生的反向电动势，与电源电压串联，共同作用于负载。这样，负载就可以获得高于电源电压的输出电压Vo。

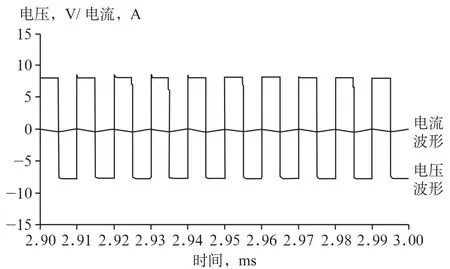
图7 电感L的电压、电流波形曲线

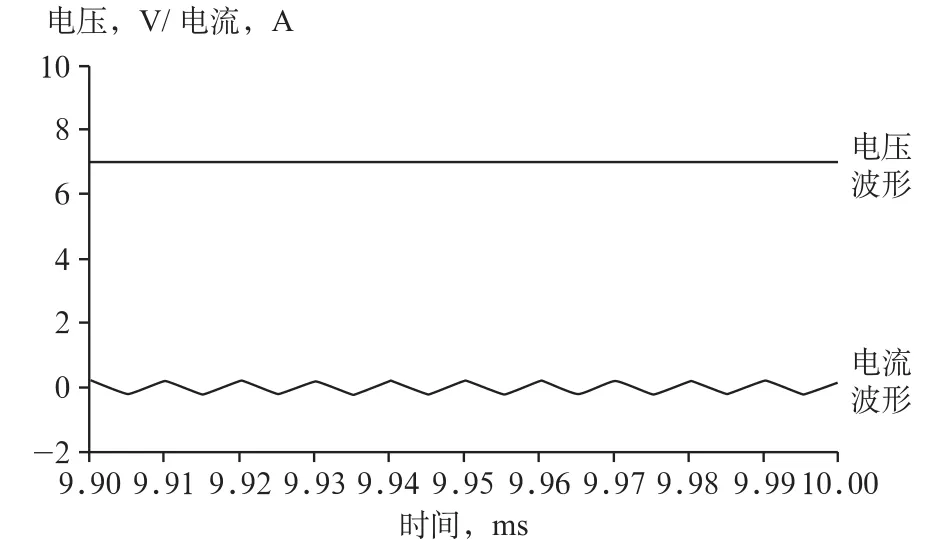
图8 电容C的电压、电流波形曲线

图9 BOOST变换器的电路结构

在开关导通的Ton=DTS期间，开关T导通，二极管D截止，电源电压VS作用于升压电感L上，电感电流iL线性增长，且满足：

当t=Ton=DTS时，iL达到最大值iLmax。在T导通期间，iL的增量ΔiL+为：

开关导通期间，由于二极管的截止作用，负载由电容C供电。若电容C的容量足够大，可使Vo变化很小。

在开关阻断的Toff=(1-D)TS期间，开关阻断，二极管导通，这时，iL和电源共同通过二极管作用于输出端负载和电容C，电容C处于充电状态。此时作用于电感L的电压为VS-Vo。由于Vo大于VS，故iL线性减小，存在以下关系：

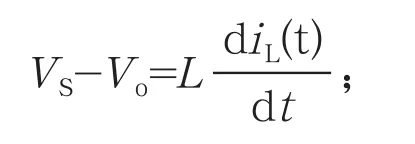
经过完整的开关阻断期间后，iL达到最小值iLmin。在开关阻断期间，iL的减小量ΔiL-为：

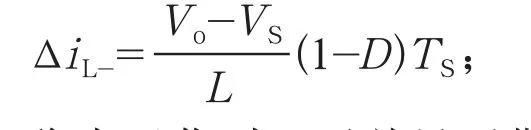
稳态工作时，开关导通期间的电感电流增量ΔiL+等于开关阻断期间的减少量ΔiL-，即ΔiL+=ΔiL-，因此输出电压Vo为：

2.2 仿真建模与验证分析

图10为依据图9的电路原理，通过OrCADPspice电路仿真软件，对升压变换器进行的仿真模拟。图9中的控制开关也通过场效应管实现。将电压探头放置在对应的位置，即可测量变换器的输出电压。在升压变换器的仿真模拟过程中，也通过变更导通比、开关频率等参量，并在同一幅图像中显示不同参量对应的输出电压波形曲线，观察参量变化对输出电压造成的影响。

图10 BOOST变换器的仿真拓扑结构

为了验证升压变换器的输出电压与导通比的关系，将导通比设置为0.1，0.2，……，0.7这7个数值，观察电压波形曲线的变化关系，如图11所示。

图11 不同导通比(0.1-0.7)状态下对应的输出电压波形

从图11显示的输出电压波形曲线中可以清晰地发现，升压变换器的输出电压Vo均大于电源电压VS。随着导通比D的增加，输出电压值也随之增大，符合升压变换器输出电压与导通比之间的关系式。同降压变换器一样，在开关导通比不变的前提 下 观 察 40kHz，60kHz，80kHz，100kHz 不同开关频率状态下的输出电压曲线，和对应的坐标轴放大图(以100kHz为例)，如图12和13所示。

图12 不同开关频率对应的输出电压波形曲线

图12是不同开关频率对应的输出电压曲线。同降压变换器一样，随着开关频率增大输出电压略微下降。最上方的电压曲线对应40kHz的开关频率，最下方的电压曲线对应100kHz的开关频率。如果将坐标轴适当放大，也能清晰地观察到实际电压变化波形曲线(以100kHz开关频率为例)，如图13所示。

将电压和电流探头放在对应的位置，即可得到图9中电感L和电容C的两端电压和流入电流波形曲线，如图14和15所示。

图13 输出电压波形曲线

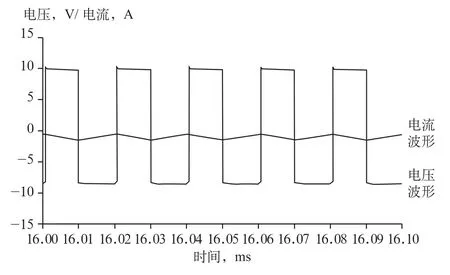
图14 电感L的电压、电流波形曲线

图15 电容C的电压、电流波形曲线

3 结论

对BUCK和BOOST变换器的电路结构、工作原理进行分析，并通过仿真建模的手段验证了模型和原理的准确性。同时，还分析了不同开关频率对输出电压造成的影响，对这2种最为基本的直流变换器有了清晰和直观的认识，为电力系统中研究直流变换器电路特性提供新的手段。

参考文献：

1 王贞艳，陈志梅，张井岗，等．基于PSpice的Buck变换器仿真教学研究[J]．电气电子教学学报，2012，34(2)：95-97.

2 茹秋生，庞美玉．PSpice对Buck变换器参数的仿真研究 [J]．制造业自动化，2009，31(7)：137-139．

3 强凯，文敏华，张锐，等．一种BUCK开关变换器的建模方法和仿真验证[J]．信息通信，2016，30(3)：53-55．

4 王英武，王俊峰，刘若宝．PWM单端正激变换器谐振磁复位分析与设计[J]．电力电子技术，2007，41(6)：43-44．

5 李锡宏，杨明超．单端正激直流变换器分析与设计探讨[J]．船电技术，2000，20(6)：15-20．