接触物系接触点的速度分解

谢剑龙

(新宾县高级中学，辽宁 抚顺 113200)

在学习速度的合成与分解时,一般会碰到两类问题.

(1) 求有杆或绳约束物系的各点速度.此类问题特征是:在同一时刻必具有相同的沿杆或绳方向的分速度,对于这类问题学生往往理解较好,问题不大．

(2) 求接触物系接触点的速度.求解这类问题学生遇到了困难．例如以下两道相似的例题.

图1

例1.如图1所示,一根长为L的轻杆OA,O端用铰链固定,另一端固定着一个小球A,轻杆靠在一个高为h的物块上.若物块与地面摩擦不计,则当物块以速度v向右运动至杆与水平方向夹角为θ时,物块与轻杆的接触点为B,求球A的线速度?

图2

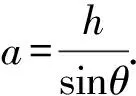
图3

例2.如图3所示,长为L的直棒一端可绕固定轴O转动,另一端搁在升降平台上,平台以速度v匀速上升,当棒与竖直方向的夹角为α时,棒的角速度为多少?

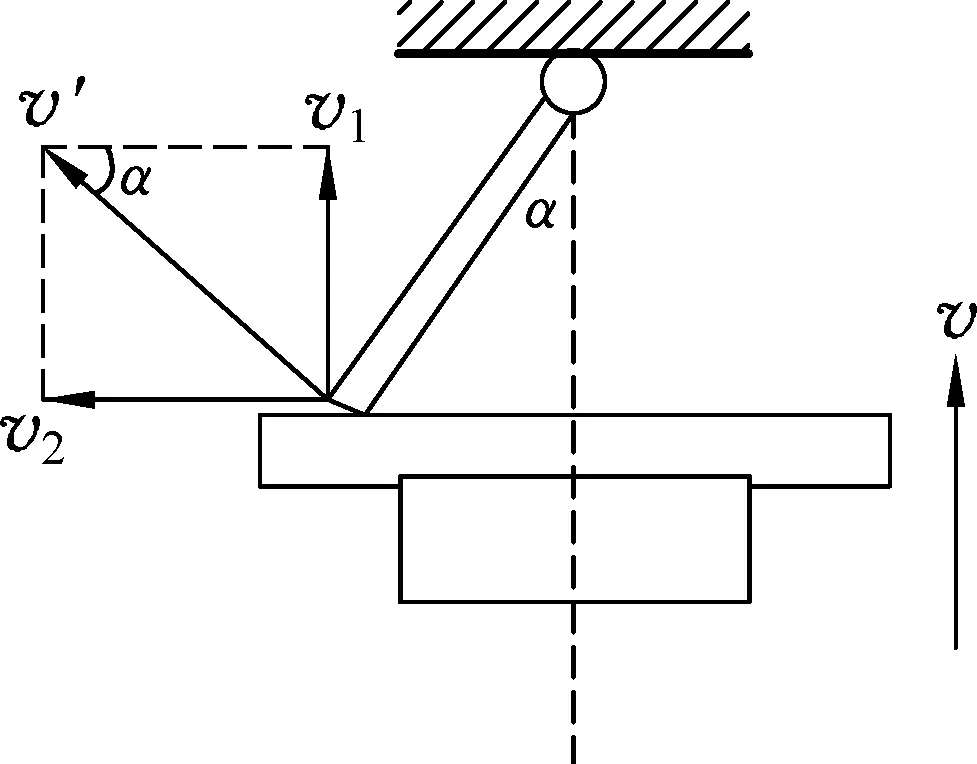
图4

对于上述两道例题表面相似却有不同,例1分解的是接触点在物块上的速度,而例2则分解的是接触点在棒上的速度．实际上,此类问题属于接触物系接触点速度的分解问题,由刚体(不能压缩和发生形变)的力学性质及接触的约束性可知,沿接触面法线方向,接触面双方必须具有相同的法向分速度,否则将分离或形变,违反接触或刚体的限制．至于沿接触面的切向接触双方是否有相同的分速度,则取决于该方向上双方有无相对滑动,若无相对滑动,则接触双方将具有完全相同的速度．

因此

图5

此类问题的特征是:沿接触面法向的分速度必定相同,沿接触面切向的分速度在无相对滑动时也相同.清楚了此类问题的原理,便可以很快地求解出此类问题.

例3.如图5所示,半径为R的半圆凸轮以等速v0沿水平面向右运动,带动从动杆AB沿竖直方向上升,O为凸轮圆心,P为其顶点.求:当∠AOP=α时,AB杆的速度.

图6

解析:由题可知,杆与凸轮在A点接触,首先确定接触点在两物体上实际运动方向．杆上A点速度vA是竖直向上的,轮上A点的速度v0是水平向右的．根据上述分析原理,两者沿接触面法向的分速度相同,如图6所示,即vAcosα=v0sinα,则vA=v0tanα.

例4.如图7所示,曲柄滑杆结构中,滑杆上有圆弧形滑槽,其半径为R,圆心在导杆BC上,曲柄OA长R,以角速度ω转动,当滑杆在在图示位置时,曲柄与水平线夹角φ=30°,求此时滑杆BC的速度.

解析:由题可知,曲柄与滑槽在A点接触,首先确定接触点在两物体上实际运动方向．曲柄上A点以O点转动,此时速度vOA与曲柄OA垂直,滑槽上的A点速度vBC水平向左．由几何关系可知vOA与vBC与法向夹角均为30°根据上述分析原理,两者沿接触面法向的分速度相同,如图8所示,即vBCcos30°=vOAcos30°,即vBC=vOA=ωR.

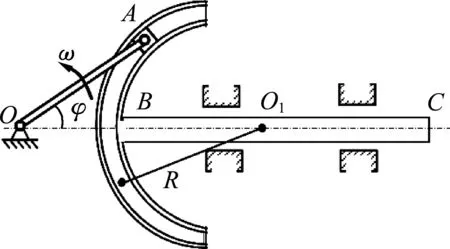
图7

图8

综上所述,在物理教学过程中,应避免让学生死记一些结论,而要让其真正地理解物理实质,明白其中道理,这样才会有利于物理教学以及学生物理思维的培养,从而达到物理教学的真正目的．

参考文献：

1 隋欣. 物体相关速度的分析方法[J]. 锦州医学院学报(社会科学版), 2006(2):23-25.

2 胡勇. 浅析速度的分解[J]. 数理化学习(高中版), 2002(17):31-32.