基于石墨烯振幅可调的宽带类电磁诱导透明超材料设计∗

王越 冷雁冰 王丽 董连和 刘顺瑞 王君 孙艳军

(长春理工大学光电工程学院,长春 130022)

1 引 言

电磁诱导透明(EIT)是三维原子系统中的一种重要的干涉现象,它能使得原来宽范围内不透明的区域中出现一个尖锐的透射窗[1,2],同时,在窄带传输窗口内,传输相位发生陡峭变化,导致“慢光”效果和非线性作用.这些特性使EIT效应在慢光器件、光信号处理、传感器、量子开关和非线性器件中具有广泛的应用.然而,三维原子系统中的EIT所需要的苛刻实验条件(即低温和高强度激光)却大大限制了EIT特性的应用.

超材料是由亚波长谐振单元组成的人工复合材料,具有自然界中材料所不具备的超常电磁特性,且其电磁特性主要取决于人工设计的单元结构.近年来,利用超材料在微波段[3,4]、太赫兹波段[5−7]及光波段[8,9]实现EIT引起了广泛关注,这种利用超材料实现EIT的效应被称为超材料类电磁诱导透明(类EIT)效应.超材料类EIT效应一般通过被称为明模式和暗模式的两类本征模的干涉作用来实现.由于主要利用等离子体谐振之间的效应而不需要另加耦合光束,因此这种用超材料实现EIT的现象成为当前研究的热点.这种明态激发暗态实现EIT的现象在波导[10]和伪局域表面波[11,12]中同样存在.然而,传统的类EIT超材料只能通过改变超材料的结构尺寸来实现对其透射窗进行调控,并且结构一旦制作完成很难改变,这就限制了类EIT超材料在实际中的应用.因此,人们希望能够利用热、电、光等方式来实现对其透射窗的主动调节和控制.2012年,Gu等[13]将半导体硅与超材料结合设计了一种类EIT超材料,通过改变外加光抽运能量实现了对其透射窗的振幅调制;2017年,Fan等[14]将二极管嵌入类EIT超材料中,通过改变外加电压实现了对其透射窗的振幅调制;同年,Xiao等[15]将石墨烯与类EIT超材料的暗模式结构相结合,通过改变石墨烯的费米能级来改变暗模式的阻尼率,从而改变了透射窗的振幅强度.

虽然上述研究通过外加主动控制材料实现了对类EIT超材料透射窗的强度调制,但都是对窄带透射窗的主动调控,在一定程度上限制了类EIT超材料的实际应用.本文基于石墨烯的电控特性提出了一种宽带可调类EIT超材料结构.在该结构中把金属线结构作为明模式,“H”型结构作为暗模式,通过增加暗模式谐振器的数量实现宽频的类EIT效应,并将石墨烯置于结构最下方,通过改变石墨烯的外加偏置电压来改变石墨烯本身的费米能级,从而实现对类EIT超材料透射窗的主动调控,并通过实验测试证明了所获得的仿真结果.该结构对太赫兹开关、太赫兹滤波器和太赫兹调制器都具有潜在的应用价值.

2 类EIT模型

为了阐明类EIT超材料的基本机理,采用(1)式所示的线性耦合的Lorentz模型对其进行分析:

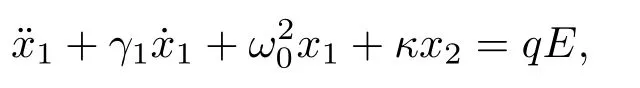
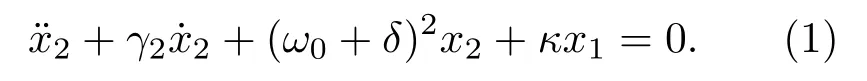
其中,x1,x2分别为明模式与暗模式的透射振幅;γ1,γ2分别为明模式与暗模式的衰减系数;ω0,ω0+δ分别为明模式与暗模式的共振频率;κ为两个模式之间的耦合系数;q为明模式与入射场E的耦合系数.

通过(1)式得出的δ,κ,γ1,γ2可以求得类EIT超材料单元结构的极化率e[16],进而可以利用公式=e/d求得类EIT超材料的极化率,其中d为类EIT超材料的等效厚度.

当类EIT超材料的等效厚度足够小时,可以近似认为入射的太赫兹波全部穿过超材料层,没有发生反射.当太赫兹波垂直入射到类EIT超材料表面时,类EIT超材料的透过率可表示为

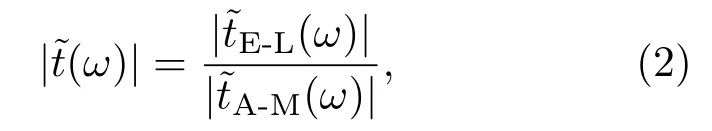
式中,为空气与介质之间的透过率,可由菲涅耳公式近似得到

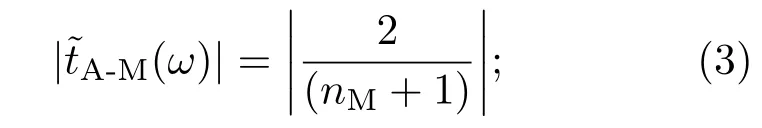
E-L(ω)为类EIT层的透过率,可以利用法布里-珀罗干涉传输方程得到

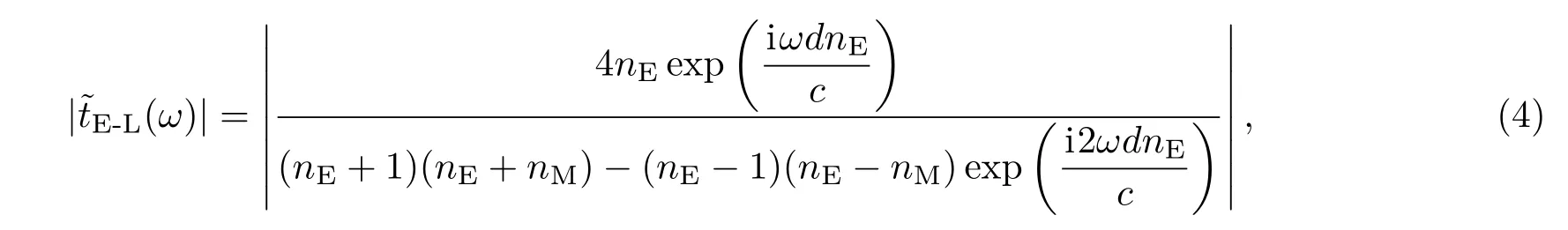
其中,为类EIT超材料层的等效折射率,nM为介质层的折射率,c为真空中的光速.

由于超材料结构层的厚度远远小于入射波长,故类EIT的远场透射系数可近似为近场透射系数:

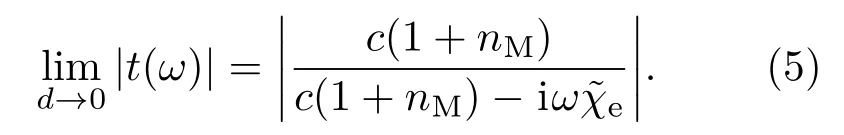
通过(1)—(5)式可以拟合出洛伦兹方程的各因素,计算结果表明,增加暗模式谐振器的数量可以使暗模衰减系数γ2减少,即降低其损耗系数,并且可以使其电偶极子的耦合系数κ增加,故可以通过此方法来增加透射窗带宽.

3 结构设计

本文提出了一种基于金属线谐振器和“H”型谐振器的类EIT超材料结构,利用金属线谐振器产生的等离子体谐振作为明模式,利用“H”型谐振器产生的电感-电容(LC)谐振作为暗模式,通过增加暗模式谐振器的数量来增强谐振器的耦合从而增加透射窗带宽,通过调节石墨烯的费米能级对其透射窗进行主动调制,其结构如图1所示.该结构由五层结构组成,由上到下依次为:金属铝结构、聚二甲基硅氧烷(PDMS)介质层、硅介质层、聚甲基丙烯酸甲酯(PMMA)介质层和石墨烯层.其结构参数为:Px=120µm,Py=140µm,D1=25µm,D2=3µm;四个“H”型的结构参数为L1=40µm,L2=28µm,L3=75µm,金属铝宽度ω=5µm;PDMS介质层的介电常数为2.35,厚度H1=35µm,金属铝厚度均为T=200 nm;硅介质层的厚度H2=50 nm,且在该结构中选用掺杂硅,作为给石墨烯施加偏置电压的另一电极[7,17,18];PMMA介质层的介电常数为4,厚度H3=50 nm.除此之外,在石墨烯层与PMMA介质层之间的边界处还设置了一条窄带的银电极,用于外加偏置电压.假设太赫兹波垂直于超材料表面沿Z轴负方向入射,利用商业软件CST对所设计的类EIT超材料进行仿真模拟.石墨烯的表面电导率(无偏置磁场时)在微波波段到可见光波段都可以由Kubo公式[19]表示:

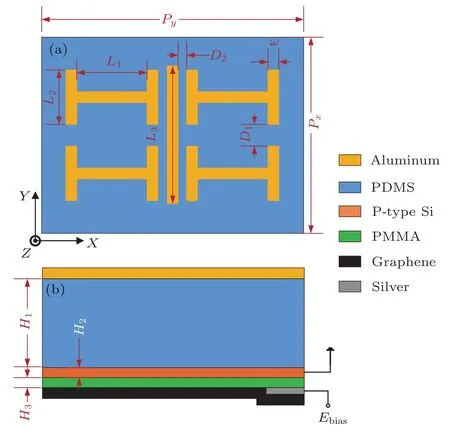
图1 类EIT超材料结构的(a)单元俯视图和(b)主视图Fig.1.Schematic diagrams of(a)top view of unit cell and(b)front view of EIT-like metamaterial.

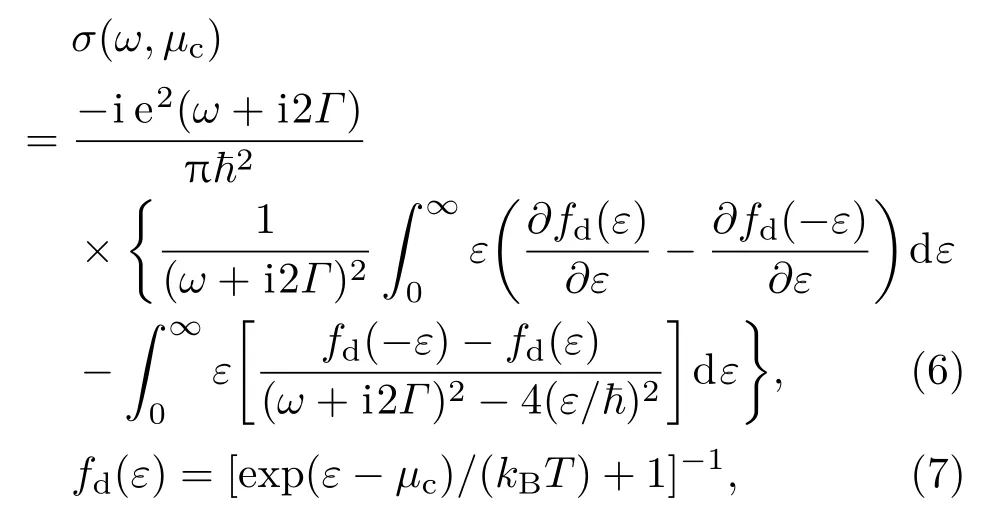
其中,kB是玻尔兹曼常数,h是狄拉克常数,fd(ε)是费米-狄拉克分布,ε是能量,µc是石墨烯的费米能级,T是开尔文温度,Γ是载流子散射率(其倒数即是弛豫时间τ).在本文中,取T=300 K,Γ=5×1012Hz.

而石墨烯的费米能级需要外加偏置电压来改变,二者的关系为

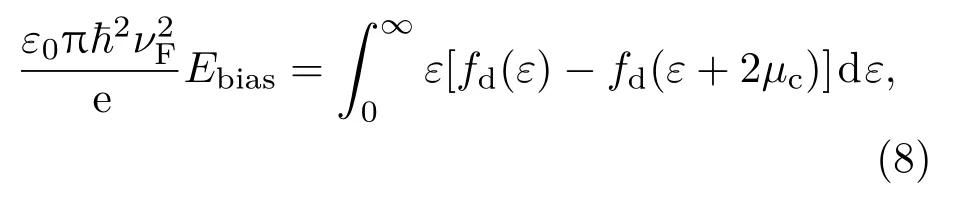
其中,Ebias为外加偏置电压,νF=106m/s为与能带无关的电子速度.在仿真过程中,将根据(6)和(7)式计算出的石墨烯电导率值导入其材料特性中,将石墨烯看作厚度为0.001µm的薄层,从而实现对石墨烯材料的设置.

4 仿真结果与分析

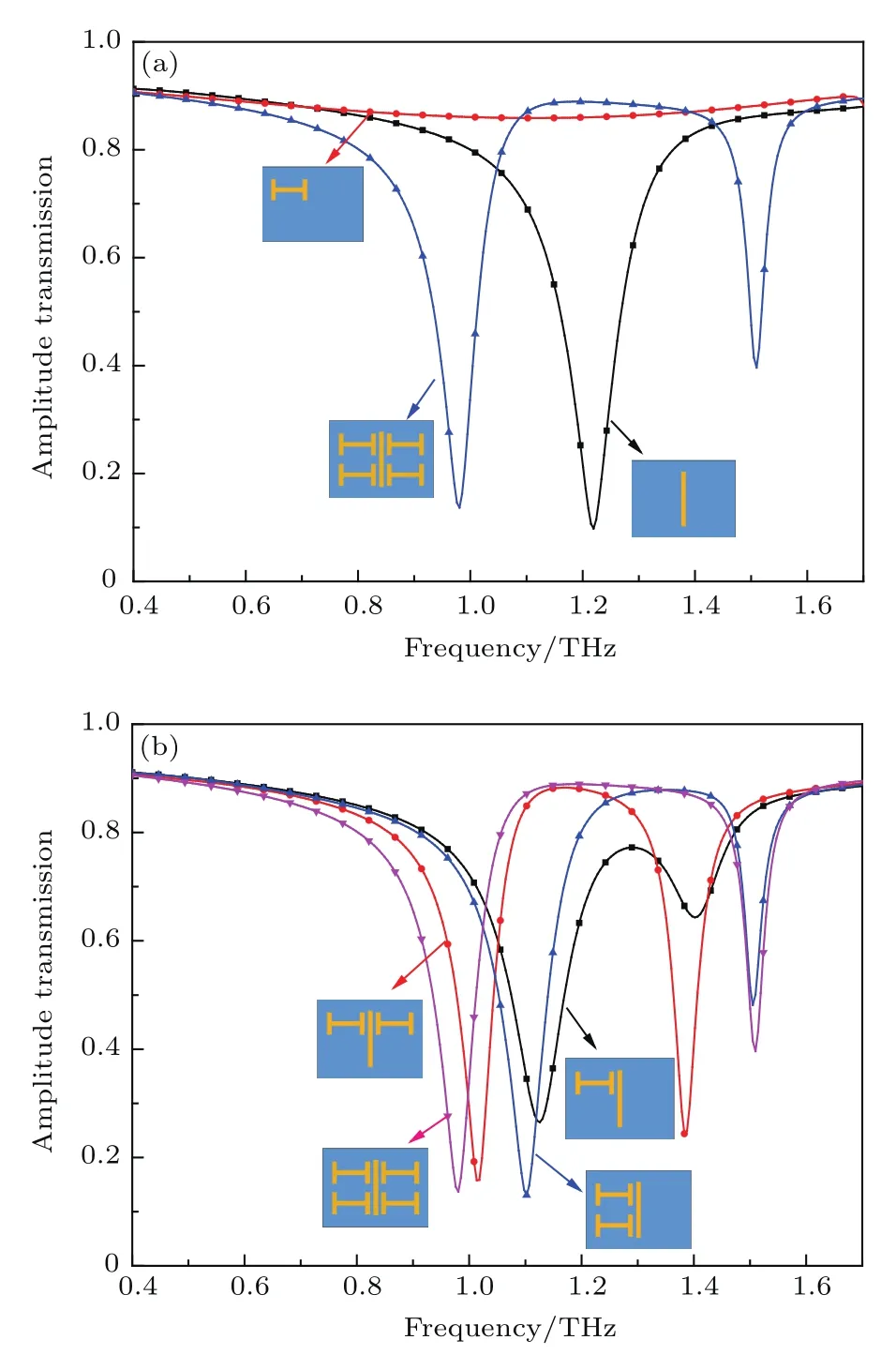
图2 当石墨烯费米能级为0 eV时,(a)“H”型谐振器、金属线谐振器和类EIT超材料的透射曲线;(b)金属线谐振器+“H”型谐振器、金属线谐振器+左右对称的“H”型谐振器、金属线谐振器+上下对称的“H”型谐振器和金属线谐振器+四个“H”型谐振器的透射曲线Fig.2.When the Fermi level of graphene is 0 eV,(a)amplitude transmission spectra of sole H-shaped resonator,sole cut-wire resonator,and EIT-like metamaterial;(b)amplitude transmission spectra of cutwire and H,cut-wire and left-right H,cut-wire and up-down H,and cut-wire and four H.

首先,分别对独立金属线谐振器、独立“H”型谐振器和石墨烯费米能级为0 eV时的组合单元结构的透射曲线进行仿真模拟,其结果如图2(a)所示.独立金属线谐振器可以在1.21 THz处产生等离子体谐振,工作在明模式;与此同时,独立“H”型谐振器无法在相同频率下产生对应的LC谐振,工作在暗模式;而将两者组合之后,金属线谐振器会被入射场激发,直接产生相应的等离子体谐振,且金属线谐振器与“H”型谐振器之间产生近场耦合,从而激发“H”型谐振器的LC谐振,最终导致明模式与暗模式相消干涉产生一个透明窗口.而且,将“H”型谐振器相对于金属线谐振器对称排布可增加暗模式间的耦合从而增加类EIT透射窗口的带宽,如图2(b)所示.随着暗模式谐振器的增加,其类EIT透射窗口的带宽也逐渐增加.

然后,对石墨烯不同费米能级下的类EIT超材料透射曲线进行仿真模拟,结果如图3所示.当石墨烯费米能级为0 eV时,其中心频率为1.26 THz,获得了在1.05—1.46 THz内透射振幅大于80%的透射窗,且平均透射振幅达到了87%左右;随着石墨烯费米能级的逐渐增加,其透射振幅随之逐渐降低,当石墨烯费米能级增加到0.5 eV时,其中心频率依旧为1.26 THz,而其在1.05—1.46 THz内平均透射振幅已经降低到了55%左右;持续增加石墨烯的费米能级,发现其透射窗的透射振幅变化幅度逐渐降低,且在石墨烯费米能级为1.5 eV时,平均透射振幅降低到了25%左右;继续增加石墨烯的费米能级,透射振幅不再产生明显变化.

最后,为了进一步研究该类EIT超材料结构的机理,对其电场分布进行了仿真计算与分析.首先在1.26 THz处设置相应的场监视器,在太赫兹波垂直入射到结构表面的条件下计算得到其表面电场分布.图4(a)—(d)分别是类EIT超材料在石墨烯费米能级为0,0.1,0.3,0.5 eV下的表面电场分布.从图4可以明显地看出,当石墨烯费米能级为0 eV时,其表面电场主要分布在四个“H”型谐振器上,而此时金属线谐振器上的电场被完全抑制,产生了类EIT效应.随着石墨烯费米能级的逐渐提高,一方面导致类EIT超材料的表面电场不仅分布在四个“H”型谐振器上,而且在金属线谐振器上的电场分布也在逐渐增加,类EIT效应逐渐减弱,透过曲线逐渐平缓.另一方面,由于石墨烯表面电导率随费米能级的增加而增强,导致类EIT超材料的表面金属结构与底层石墨烯结构的谐振也逐渐增强,如图5所示.随着类EIT超材料的反射变化幅度减小,对入射太赫兹波的吸收逐渐增强,进而透射振幅逐渐减少,最终实现了对其宽频透射窗的调制.

图3 不同石墨烯费米能级下对应的透射曲线Fig.3.Amplitude transmission spectra with different Fermi level of graphene.

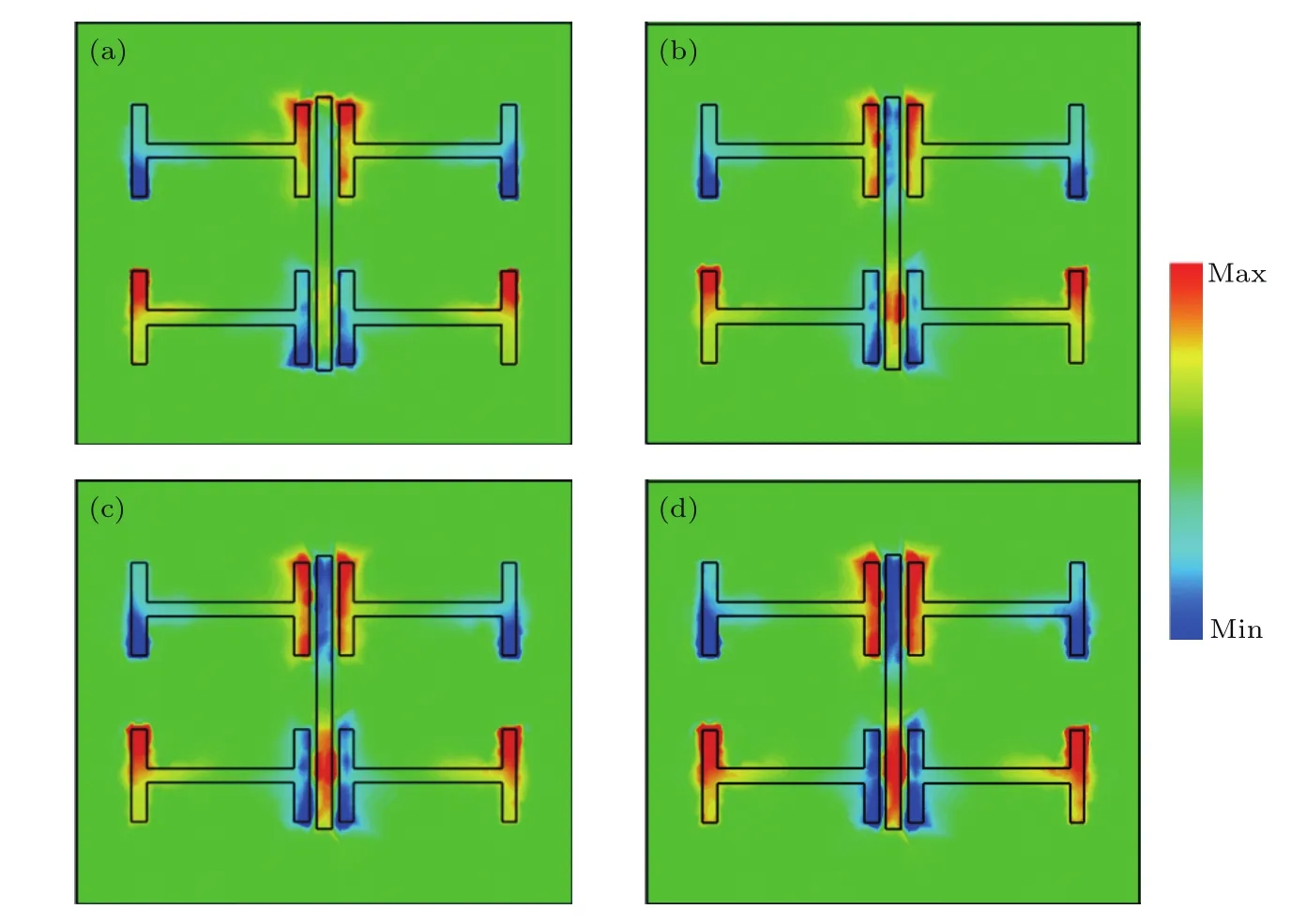
图4 当石墨烯费米能级为(a)0,(b)0.1,(c)0.3和(d)0.5 eV时,在中心频率1.26 THz处的电场分布Fig.4.Distribution of electric field at central frequency of 1.26 THz when Fermi level of graphene is(a)0,(b)0.1 eV,(c)0.3 eV,and(d)0.5 eV.

图5 不同石墨烯费米能级下对应的反射曲线Fig.5.Amplitude re flection spectra under different Fermi levels of graphene.

5 实验与测试

实验中,首先采用磁控溅射的方式在35µm PDMS薄膜的一侧表面沉积一层200 nm的铝,在PDMS薄膜的另一侧利用等离子体激活的化学气相沉积法沉积一层厚度为50 nm的轻度掺杂P型硅[20]并引出调制电极;然后在硅层的下方选用浓度为4%PMMA溶液以3000 r/min旋涂40 s制成PMMA隔离层,在PMMA层下方,采用磁控溅射的方法获得厚度为40 nm的银电极,并采用湿法转移技术将化学气相沉积法生长的单层石墨烯薄膜转移到PMMA层上方,同时保证石墨烯一部分与银电极重叠以引出调制电极;最后采用微光刻技术将铝层加工成所设计的超材料结构,加工结果如图6(a)所示.

在完成器件制备后,选用太赫兹时域光谱系统(系统型号:API T-Ray5000)进行超材料的太赫兹透射光谱测量.测试原理图如图6(b)所示.把类EIT超材料放置在样品架上,随后将两根导线分别连入直流电压源,之后太赫兹脉冲从太赫兹发射器射出,最后由太赫兹接收器接收.控制调制电压在0—55 V(即石墨烯费米能级约为0—0.5 eV)变动,从而改变石墨烯的费米能级,并探测该结构在不同调制电压下的太赫兹透射光谱.

实验结果如图7所示.当外加偏置电压为0 V时,即石墨烯费米能级为0 eV时,其中心频率为1.26 THz,在1.05—1.46 THz内获得了透射率大于80%的透射窗;随着外加偏置电压逐渐增加到8和55 V时,即石墨烯费米能级分别为0.2和0.5 eV时,其中心频率依旧为1.26 THz,而其在1.05—1.46 THz内的平均透射振幅降低到了70%和58%左右.测试结果与图3中仿真结果的变化趋势一致,但实验中透射窗的强度与仿真结果仍存在一定的偏差,出现偏差的主要原因有:实验中介质层的实际损耗系数大于仿真时设置的损耗系数;实验制作中的结构参数与仿真时的参数存在差异;测试过程中石墨烯的外加偏置电压是根据石墨烯的费米能级由(7)和(8)式求出的近似电压.

图6 (a)类EIT超材料实物图;(b)太赫兹透射光谱测试原理图Fig.6.(a)Microscopic image of fabricated EIT-like metamaterial;(b)test schematic of terahertz transmission spectrum.

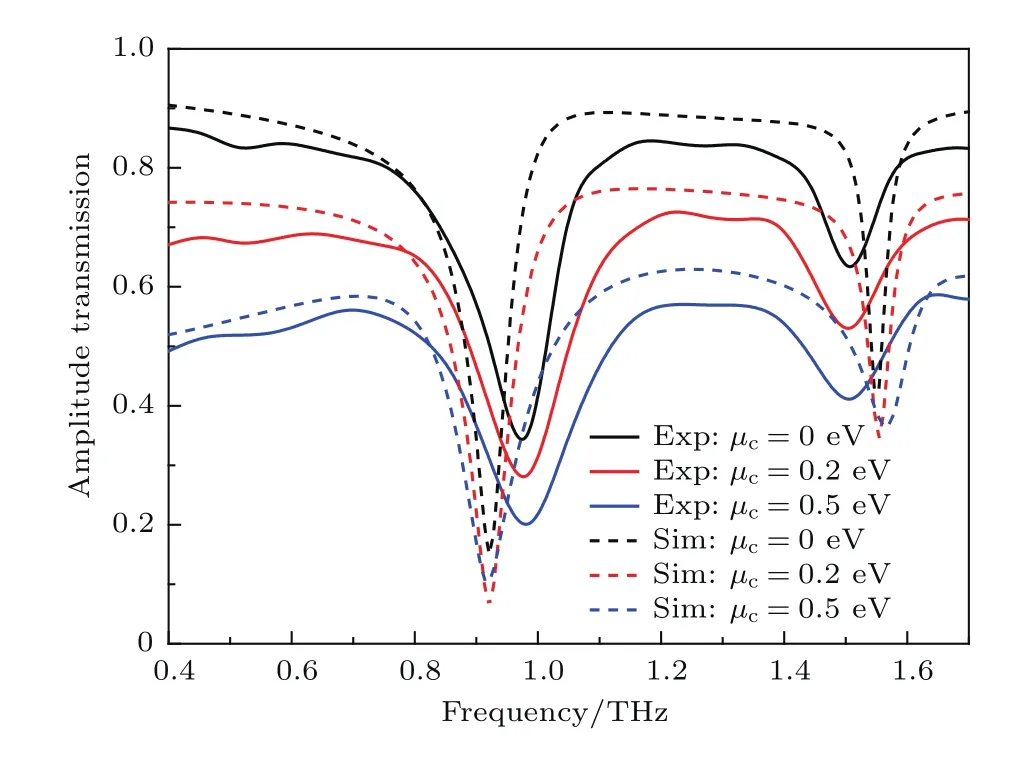
图7 不同石墨烯费米能级下的透射测试曲线和透射仿真曲线Fig.7.Transparency data obtained by experimental measurement and simulation under various Fermi levels of graphene.

6 结 论

本文基于石墨烯的电控特性提出了一种由金属线谐振器和“H”型谐振器组成的宽带可调的类EIT超材料结构.通过仿真模拟、理论计算和实验测试,证明了该结构透射窗在1.05—1.46 THz内可实现透射振幅的宽带可调特性,并通过仿真模拟该结构在1.26 THz下的电场分布对其透射机理进行了分析.该结构设计简单、调制方法简便,对太赫兹开关、太赫兹滤波器和太赫兹调制器都具有潜在的应用价值.

参考文献

[1]Marangos J P 1998J.Mod.Opt.45 471

[2]Fleischhauer M,Imamoglu A,Marangos J P 2005Rev.Mod.Phys.77 633

[3]Zhang L,Tassin P,Koschny T,Kurter C,Anlage S M,Soukoulis C M 2010Appl.Phys.Lett.97 241904

[4]Hu S,Liu D,Lin H,Chen J,Yi Y Y,Yang H 2017J.Appl.Phys.121 123103

[5]Zhao Z Y,Song Z Q,Shi W Z,Peng W 2016Opt.Mater.Express6 2190

[6]Chen X,Fan W H 2016Opt.Mater.Express6 2607

[7]He X J,Yang X Y,Li S P,Shi S,Wu F M,Jiang J X 2016Opt.Mater.Express6 3075

[8]Wang J Q,Yuan B H,Fan C Z,He J N,Ding P,Xue Q Z,Liang E J 2013Opt.Express21 25159

[9]Huang Z,Dai Y Y,Su G X,Yan Z D,Zhan P,Liu F X,Wang Z L 2018Plasmonics13 451

[10]Chen L,Gao C M,Xu J M,Zang X F,Cai B,Zhu Y M 2013Opt.Lett.38 1379

[11]Chen L,Wei Y M,Zang X F,Zhu Y M,Zhuang S L 2016Sci.Rep.6 22027

[12]Chen L,Xu N N,Singh L,Cui T J,Singh R,Zhu Y M,Zhang W L 2017Adv.Opt.Mater.5 1600960

[13]Gu J Q,Singh R,Liu X J,Zhang X Q,Ma Y F,Zhang S,Maier S A,Tian Z,Azad A K,Chen H T,Taylor A J 2012Nat.Commun.3 1151

[14]Fan Y C,Qiao T,Zhang F L,Fu Q H,Dong J J,Kong B T,Li H Q 2017Sci.Rep.7 40441

[15]Xiao S,Wang T,Liu T T,Yan X C,Li Z,Xu C 2018Carbon126 271

[16]Zhang S,Genov D A,Wang Y,Liu M,Zhang X 2008Phys.Rev.Lett.101 047401

[17]He X Y 2015Carbon82 229

[18]Huang X J,Hu Z R,Liu P G 2014AIP Adv.4 117103

[19]Fallahi A,Perruisseau-Carrier J 2012Phy.Rev.B86 195408

[20]Ren L,Zhang Q,Yao J,Sun Z Z,Kaneko R,Yan Z,Nanot S L,Jin Z,Kawayama I,Tonouchi M,Tour J M,Kono J 2012Nano Lett.12 3711