基于复杂网络动力学模型的无向加权网络节点重要性评估

孔江涛 黄健 龚建兴 李尔玉

(国防科技大学机电工程与自动化学院,长沙 410073)

1 引 言

随着时代的发展,人们的生产生活与各种复杂网络系统的联系越来越紧密,如计算机网络、交通网络、电力网络、社交网络等,这些复杂网络系统给人们提供了极大的便利.但是伴随复杂网络系统的危害也时有发生,如俄亥俄州克利夫兰市的几条高压线路短路造成了北美大停电事故,WannaCry勒索病毒的全球大爆发,传染病的爆发和舆情危机等.网络带来的危害通常是从一小部分节点开始最终蔓延扩展到整个网络系统[1,2].复杂网络系统中各个节点所处的拓扑结构不同,甚至各个节点的特性也不相同,使用定量方法对复杂网络中节点的重要性进行分析意义重大,可有效指导人们对重要节点进行性能改进和防护加强,达到避免危害发生或控制危害程度的目的.另一方面,分析出复杂网络中重要节点可以帮助用户确定雇佣社交网络中哪些账号进行营销效果最好、打击网络中的哪些节点破坏效果最佳等.近年来,关于复杂网络中节点的重要性评估方法已成为复杂网络理论研究的一个重要方面,已有的研究成果多集中在挖掘复杂网络的拓扑结构信息上,而基于网络动力学模型的节点重要性评估方法研究成果较少,复杂网络中的节点重要性评估方法的研究仍具有很大的空间.

复杂网络的重要节点是指相比网络其他节点而言,能够在更大程度上影响网络的结构与功能的一些特殊节点[3],现已衍生出很多复杂网络节点重要性的评估方法.从网络拓扑结构出发的经典方法包括度中心性方法[4]、介数中心性方法[5]、K-壳分解法[6]、PageRank方法[7]等.度中心性计算高效,但是只能反映复杂网络局部信息.Chen等[8]提出了半局部中心性,其涉及了节点的四阶邻居信息.阮逸润等[9]提出了一种考虑节点度以及邻居节点拓扑重合度的节点重要性评估方法,该方法只需获取节点两跳内邻居就可以计算出节点的重要度值.介数中心性仅考虑了最短路径,Freeman[10]进一步提出了流介数中心性,他认为网络中所有不重复的路径中,经过节点的路径比例越大该节点就越重要.同时,可将所有路径通过某节点的路径都赋予一个权重,并对这些权重求和用于表示该节点的重要程度[11].PageRank方法中假设节点跳转概率相同并且算法参数依靠经验决定,LeaderRank方法很好地解决了这些问题,实验表明LeaderRank方法拥有更好的收敛性和更强的鲁棒性[12].此外,还有HITs(hyperlink-induced topic search)算法、基于节点移除的评估方法和基于Dempster-Shafer(D-S)证据理论的评估方法.HITs算法从权威值和枢纽值两个维度表示节点的重要性[13].基于节点移除的评估方法则是通过考察移除节点后网络结构的破坏程度,破坏程度越大,对应的节点越重要[14].基于D-S证据理论的评估方法利用证据理论将节点的度和节点的强度进行融合,利用融合后形成新指标表示节点的重要程度[15].类似的多指标融合的方法还有基于多重影响力矩阵的有向加权网络节点重要性评估方法[16].仅仅从拓扑结构角度出发去评估节点重要性没有考虑到每个节点的自身特点.

考虑网络拓扑结构的同时,对节点的行为和特性进行动力学建模,可以得到复杂网络动力学模型.基于复杂网络动力学模型进行节点重要性评估也是研究热点.目前较为成熟的用于节点重要性评估的动力学模型是传染病模型,在该类模型中节点是指可以得传染病的人,并且这些人具有自愈的能力,其中主流的模型有病人可以反复多次得病的SIS模型[6]和病人生病治愈后具有终生免疫力的SIR模型[17],基本思路是依次设置不同节点处于感染状态,并通过对比一定时间内病毒传播的速度和范围来评价每个节点的重要程度.Yan等[18]在加权无标度网络上的病毒传播实验表明网络拓扑结构影响疾病传播过程的同时,强度越大的节点越易被感染.随着复杂网络研究的深入,级联失效现象逐渐引起了人们的重视,级联失效模型是在复杂网络拓扑结构的基础上赋予节点一定的负载能力,并设置节点因负载过大失效后其负载重新分配机制,然后通过测试不同节点失效后网络级联失效的程度进行节点的重要性评估[19].杜文举等[20]建立了公交网络耦合映象格子模型用于描述网络级联失效行为,并通过实验说明节点度越大越容易造成网络全局故障.在复杂网络可控性研究领域,可以将最佳驱动节点看作重要的节点[9].Liu等[21]发现在节点自身动力学模型相同的复杂网络动力学系统中,驱动节点倾向于避免高度节点.进一步,Jia和Barabási等[22]对最小的驱动节点集进行研究,发现节点的入度越大,其成为驱动节点的可能性越小,节点是否为驱动节点与节点的出度无关.基于动力学模型的方法包含网络拓扑结构信息,也包含对节点的建模,并且能够在时域上对网络状态的变化进行描述,所以评价比较全面.但是目前已有的基于动力学模型的网络节点重要性评估方法也有不足.级联失效模型主要适用于会发生“雪崩”式故障的复杂网络.利用传染病模型进行复杂网络节点评估时,疫情的传播最后应具有稳定规模,稳定的疫情规模是进行节点重要性评估的前提,基于复杂网络可控性研究领域的动力学模型进行节点重要性分析时同样要求建立的复杂网络动力学模型稳定可控,但是针对复杂网络建立其对应的满足节点重要性评估条件的传染病模型和动力学模型困难,故这两种方法难以直接推广使用.

本文提出了基于复杂网络动力学模型的节点重要性评估方法,其适用于任意无向加权网络的节点重要性评估,具有良好的通用性.复杂网络的正常状态是所有节点都处于各自的稳定平衡态,节点偏离自己的稳定平衡态后,这种非稳定状态会通过网络的拓扑结构影响到整个网络.本文提出的节点重要性评估方法就是根据节点偏离稳定平衡态对整个网络的影响程度来确定节点的重要性,对网络的影响程度越大,对应的节点越重要.本文提出的方法不仅包含了网络拓扑结构信息,还包含了单个节点的动力学模型,并通过仿真方法对网络动力学模型状态变化进行分析,最终完成对节点重要性的评估.本文的具体结构如下:第二部分提出了无向加权网络对应的复杂网络动力学模型的构建方法,并证明了构建的动力学模型都是大范围内一致渐近稳定的,同时建立了基于复杂网络动力学模型的节点重要性评价指标;第三部分提出了基于复杂网络动力学模型进行节点重要性评估的扰动测试方法和破坏测试方法;第四部分对本文提出的节点重要性评估方法进行实验验证;最后给出结论.

2 复杂网络动力学模型的构建及节点重要性评估标准

本节首先介绍构建无向加权网络动力学模型的方法,进一步利用李雅普诺夫稳定性定理证明该类复杂网络动力学模型是大范围内一致渐近稳定的,最后提出基于动力学模型的节点重要性评估标准.

2.1 复杂网络动力学模型构建方法

线性耦合常微分方程组在时空复杂网络和复杂系统研究中有广泛的应用,本文用线性耦合常微分方程组描述复杂网络动力学模型.给定无向加权网络模型为三元组G={V,E,W},式中V={v1,v2,···,vn}表示节点集合.文中网络模型节点个数都为n;E={e1,e2,···,em}表示边的集合,(vi,vj)∈E表示从节点vi到节点vj的连边;为连边的权重矩阵,其中wii=0且wij>0,wij(ij)表示边(vi,vj)的权重.无向加权网络的权重矩阵W满足

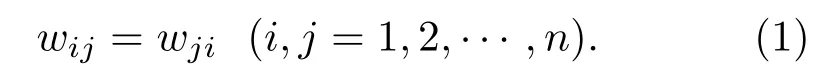
根据W可以得出无向加权图的拉普拉斯矩阵其中

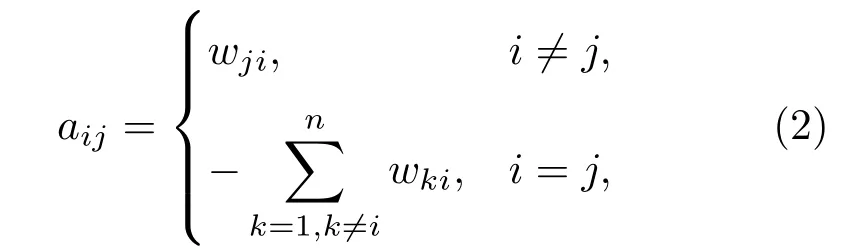
显然有本文假定权重值越大,其连接的节点关系越紧密.对复杂网络中的节点vi建立如下线性耦合常微分方程:

其中,xi(t)∈R表示节点vi在t时刻的状态,c>0表示网络整体耦合强度,aij为网络拉普拉斯矩阵对应位置上的元素.本文设定c=1,fi(·):R→R是一个连续函数,为节点vi的自身动力学模型.

复杂网络节点的自身动力学模型可以分为两类.如果复杂网络中所有节点的自身动力学模型都相同,那么构建的复杂网络动力学模型就是同质网络.如果复杂网络中的节点都有各自的自身动力学模型,那么构建的复杂网络动力学模型就是异质网络.构建同质网络时,任意节点vi的自身动力学模型如下:

构建异质网络时,每个节点的自身动力学模型根据实际问题进行确定,节点自身动力学模型具有一个可调参数,节点vi的自身动力学模型如下:

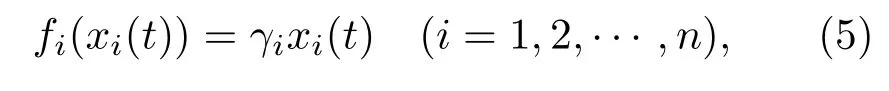
其中γi∈R为节点vi自身动力学模型的可调参数,其取值范围为γi<0(i=1,2,···,n).γi的取值反映节点自身的稳定性.节点自身动力学模型的可调参数|γi|值大时,增益小,抗干扰能力强,并且恢复稳定的时间短,所以稳定性好.

本文提出的建立复杂网络动力学模型的方法也适用于对称有向加权网络.对称有向加权网络,其权重矩阵为对称矩阵,根据(2)式可以得出其拉普拉斯矩阵,进而建立(3)式所示的对称有向加权网络动力学模型.

2.2 复杂网络动力学模型稳定性分析

建立复杂网络动力学模型后,需要对动力学模型的稳定性进行分析.正常运转时复杂网络系统处于稳定的平衡态.只有建立的动力学模型稳定,才能通过测量复杂网络动力学模型偏离稳态的程度衡量网络中各个节点的重要性,所以建立稳定的复杂网络动力学模型是后续展开节点重要性分析的基础.本文根据李雅普诺夫稳定性定理,对复杂网络动力学模型的稳定性进行证明.这里先介绍三个定理.

定理1[24]如果方阵是实矩阵,满足则|B|>0.

定理2如果方阵是实对称矩阵,其特征值都为实数,且存在正交矩阵Q,使QTBQ=Q−1BQ为对角阵.

定理3[25]设有一动态系统,其状态方程为

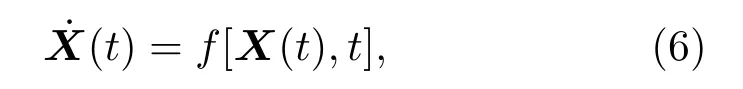
其中X(t)∈Rn为状态向量,f(·):Rn×T→Rn是状态和时间的函数.如果系统在平衡状态Xe的某些邻域内存在一个正定的具有连续一阶偏导数的标量函数V[X(t),t],其导数[X(t),t]是负定的,当∥X∥→∞时,有V[X(t),t]→∞,则该平衡态是大范围内一致渐近稳定的.

为了便于分析,将无向加权网络的动力学模型写成状态方程:

其中X(t)=(x1(t),x2(t),···,xn(t))T, 偶和强度c=1,F=diag{γ1,γ2,···,γn}为对角矩阵,γi(i=1,2,···,n)为节点vi自身动力学模型的可调参数,A为复杂网络的拉普拉斯矩阵.取复杂网络动力学模型的平衡状态Xe=0,定义李雅普诺夫函数

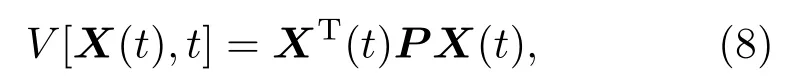
其中P∈Rn×n为正定矩阵.取P为单位矩阵,显然正定,当X(t)Xe时,有V[X(t),t]>0,并且当∥X∥→∞时,有V[X(t),t]→∞.

进一步,对V[X(t),t]求导可以得到

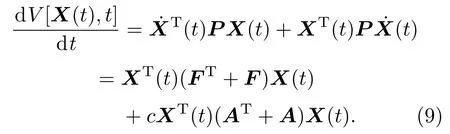
设V1[X(t),t]=XT(t)(FT+F)X(t),V2[X(t),t]=cXT(t)(AT+A)X(t).下面对V1[X(t),t]和V2[X(t),t]分别进行分析.对于V1[X(t),t],由于F为一个对角矩阵且对角元γi<0,所以当X(t)Xe有

对于V2[X(t),t],设矩阵且A′=为对称矩阵,其任意特征值都非正实数.因为

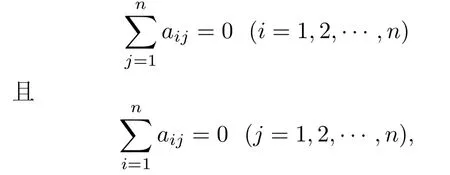
存在n维列向量满足A′Y′=0Y′,所以0是矩阵A′的特征值.假设矩阵A′存在一个特征值λ>0,则有|λI−A′|=0,其中I为单位阵.矩阵A′中任意对角元任意非对角元并且

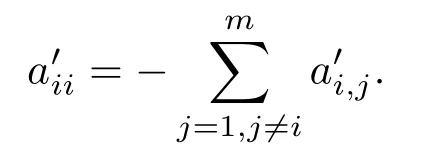
设矩阵所以矩阵D的任意对角元素显然有

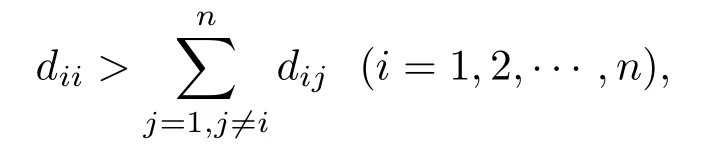
根据定理1可得|D|=|λI−A′|>0,所以矩阵A′不存在正实数特征值.同时A′为对称实矩阵,根据定理2可知,其可进行正交对角线化,假设A′的特征值为0=λ1>λ2>···>λn以及其正交化矩阵为Φ,然后有

其中ΦX(t)=(z1(t),z2(t),···,zn(t))T.故当X(t)Xe时有V1[X(t),t]<0 和V2[X(t),t]6 0,所以˙V[X(t),t]<0,根据定理3可知,本文针对无向加权网络和对称有向加权网络构建的动力学模型簇都是大范围内一致渐近稳定的,并且该模型簇具有相同的稳定平衡状态Xe=0.

值得注意的是,构建的动力学模型的李雅普诺夫函数的导数满足

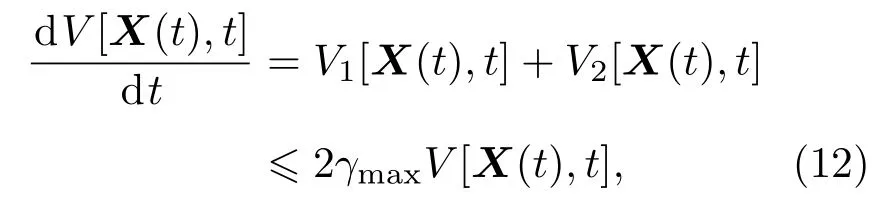
所以对应的李雅普诺夫函数成指数级收敛,

其中γmax<0.指数级收敛特性保证了构建的动力学模型能够在有限的时间内恢复稳定.此外,当有向加权网络图的权重矩阵满足

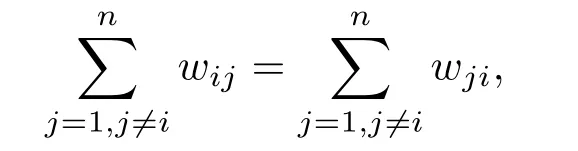
可以称其为有向加权平衡网络图[26],对于有向加权平衡网络,利用本文提出的构建复杂网络动力学模型方法构建的动力学模型同样是大范围内一致渐近稳定的.

2.3 基于复杂网络动力学模型的节点重要性评估标准

本文利用复杂网络动力学模型描述复杂网络中节点间的相互影响活动.当单个节点状态变化时,这种变化会在网络中传播,进而影响网络整体平衡态,这种平衡态的变化可以用来衡量节点的重要性.通过对每个节点进行测试,测量测试开始至动力学模型重新稳定的时期内动力学模型偏离平衡态Xe的程度.测试的节点致使复杂网络动力学模型偏离稳定平衡态的程度越大,该节点的重要程度越高.基于复杂网络动力学模型,本文建立了两级指标衡量复杂网络偏离稳定平衡态的程度.首先是复杂网络动力学模型的偏离均值,该指标衡量模型总体的偏离稳定平衡态Xe的距离.假设测试模型为S,需要分析其在测试开始至稳定的时期T内的状态变化情况.复杂网络动力学模型的偏离均值计算公式如下:

其中n为复杂网络动力学模型中的节点个数;T0为测试开始时间;∆t为时间步长,且有m∆t=T.复杂网络动力学模型的基于偏离均值的方差是衡量所有节点在偏离均值附近波动的情况.基于偏离均值的方差的计算公式如下:

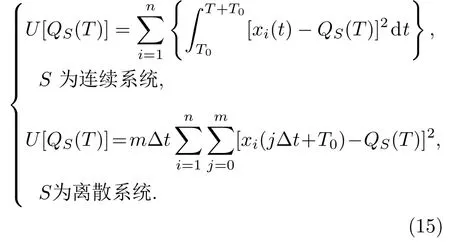
基于复杂网络动力学模型进行节点重要性评估时,本文提出了两种测试方法,分别为扰动测试方法和破坏测试方法,具体见第3节.需要说明的是:在同质网络扰动测试中,仅使用基于偏离均值的方差作为节点重要性评估的评估指标;而在同质网络破坏测试、异质网络扰动测试和破坏测试中,则是先比较复杂网络动力学模型的偏离均值,如果偏离均值无法区分节点重要度,进一步使用基于偏离均值的方差.无论是偏离均值还是基于偏离均值的方差,都是值越小对应的节点重要性越低.

3 基于复杂网络动力学模型的节点重要性评估方法

在同质和异质网络中,节点自身动力学模型描述节点自身的工作状态变化,其受影响的性质可分为两种:一种是节点受到干扰后并未被破坏,可以自行恢复;另一种是受到扰动后节点被破坏,即节点状态始终处于一种非正常状态.为了在两种不同情况下进行节点重要性评估,本文分别提出了扰动测试方法和破坏测试方法.

3.1 基于复杂网络动力学模型的扰动测试方法

扰动测试方法是对复杂网络动力学模型中的测试节点施加一个脉冲输入,然后观察自脉冲输入起到复杂网络动力学模型重新稳定的时期T内网络中各个节点的状态变化,对节点vi进行扰动测试的情形如图1所示.

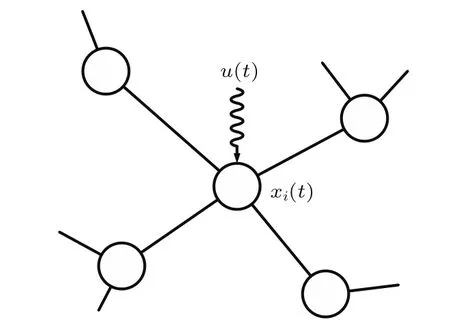
图1 扰动测试示意图Fig.1.Schematic diagram of the perturbation test.

对(7)式所示的复杂网络动力学模型进行扰动测试,其对应的扰动测试模型如下:

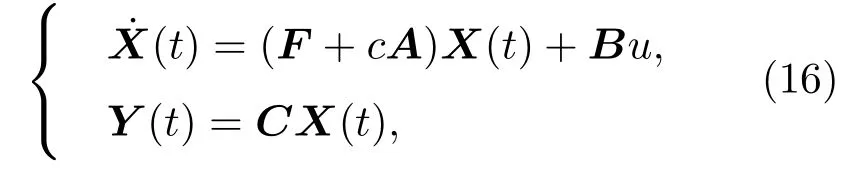
其中F,c和A与(7)式中的定义相同;B=[b1,b2,···,bn]为输入矩阵,如果测试节点为vi,则bi=1 并且bj=0(ji;j=1,2,···,n);u为脉冲输入;C为n阶单位矩阵.在扰动测试模型中,节点的初始状态为X(T0)=Xe,由于C为单位阵,节点的状态即测试模型的输出Y(t).在对同质网络中任意节点进行扰动测试时,对应的复杂网络扰动测试模型都具有相同的偏离均值,所以需要利用基于偏离均值的方差区分不同节点的重要性.初始状态为零的情况下,(16)式表示的同质网络扰动测试的偏离均值为

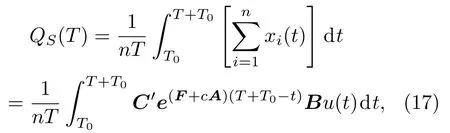
其中,C′是一个元素都为1的n维行向量,e(F+cA)(T+T0−t)为状态转移矩阵.因为拉普拉斯矩阵A满足所以有

其中由(18)式可知,对于任意两个输入矩阵和只要有那么输入矩阵B1和B2对应的动力学模型的偏离均值相等.在同质网络扰动测试中,不同节点的扰动测试动力学模型的输入矩阵元素加和都为1,所以同质网络的所有扰动测试动力学模型都有相同的偏离均值.

3.2 基于复杂网络动力学模型的破坏测试方法

破坏测试是指使测试节点状态始终处于某个固定的非平衡态,如图2所示,当设置节点vi为破坏节点,则有节点状态xi(t)≡1,该节点非稳定状态会直接影响与它相连的邻居节点,进而影响整个网络的稳定平衡态,观察自测试节点被破坏起到复杂网络动力学模型重新稳定的时期T内各个节点的状态变化.

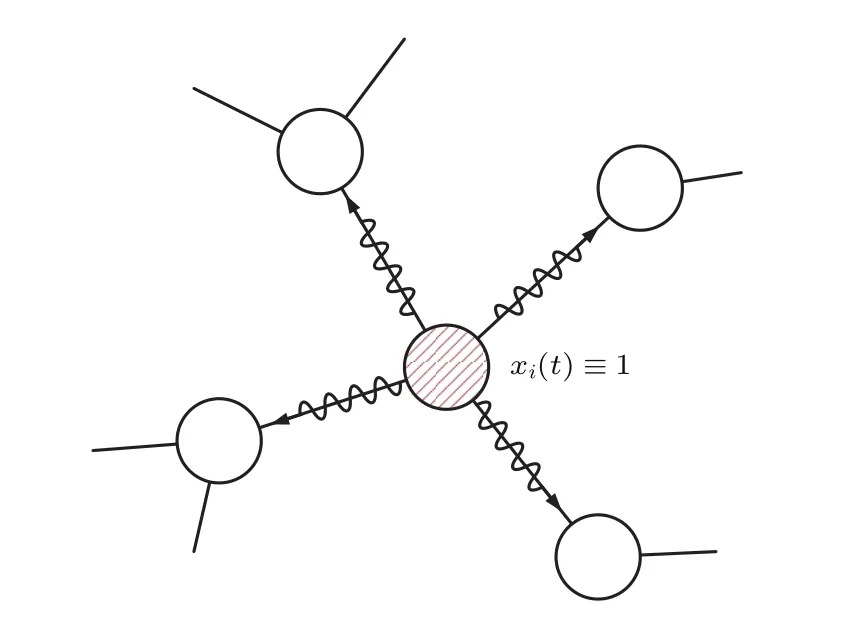
图2 破坏测试示意图Fig.2.Schematic diagram of the destructive test.

针对(7)式所示复杂网络动力学模型进行破坏测试,如果测试节点为vi,其对应的破坏测试模型如下:

参照2.2节动力学模型稳定性分析的过程,可以证明该状态演变模型除测试节点外的其他节点状态是大范围内一致渐近稳定的.在进行破坏测试过程中,如果测试节点为vi,节点的初始状态都设定为并且满足(ji;j=1,2,···,n),并且有最后对不同节点的破坏测试数据进行分析,按照先比较偏离均值,再比较基于偏离均值的方差的顺序,对节点进行重要性评估.

4 实验分析

基于动力学模型的节点重要性评估方法的验证实验可以分为同质网络的扰动测试、同质网络的破坏测试、异质网络的扰动测试和异质网络的破坏测试共四类.本节具体的安排是通过实验对同质网络扰动测试方法的有效性进行解释说明;进一步选取度中心性方法、互信息方法[27]、PageRank[28]方法和介数中心性方法与同质网络破坏测试方法进行比较,说明同质网络破坏测试方法的有效性;而在异质网络的扰动测试和破坏测试中,本文通过设置不同的节点自身动力学模型可调参数并进行分组实验,对分组实验的评估结果进行比较分析,说明异质网络的扰动测试方法和破坏测试方法的有效性.

4.1 扰动测试的有效性分析

扰动测试分为同质网络的扰动测试和异质网络的扰动测试,本文分别利用ARPA(advanced research project agency)网络和DWS(Dobbs-Watts-Sabel)网络进行扰动测试.对ARPA网络的边赋予权重[29],得到如图3所示的无向加权ARPA网络并建立其同质网络动力学模型.依次对每个节点施加脉冲输入,计算脉冲输入下测试模型的基于偏离均值的方差,具体结果如图4所示.扰动测试方法下,节点v9,v8,v10比较重要,从图3可以发现,这些节点属于边缘节点,这些节点的度比较小,而节点v2,v3,v14受到脉冲输入后,对应的扰动测试模型的基于偏离均值的方差较小,重要程度低,所以结论是节点度数低的重要程度高,而节点度数高的重要程度低.可以看出扰动测试的结论与Jia和Barabási[22]发现驱动节点倾向于避免高度节点的结论一致.本质原因是当节点的度较高时,与其相连接的节点多,在不破坏该节点的前提下,该节点会将冲击向周围节点分摊并借助整个复杂网络快速恢复稳定状态.

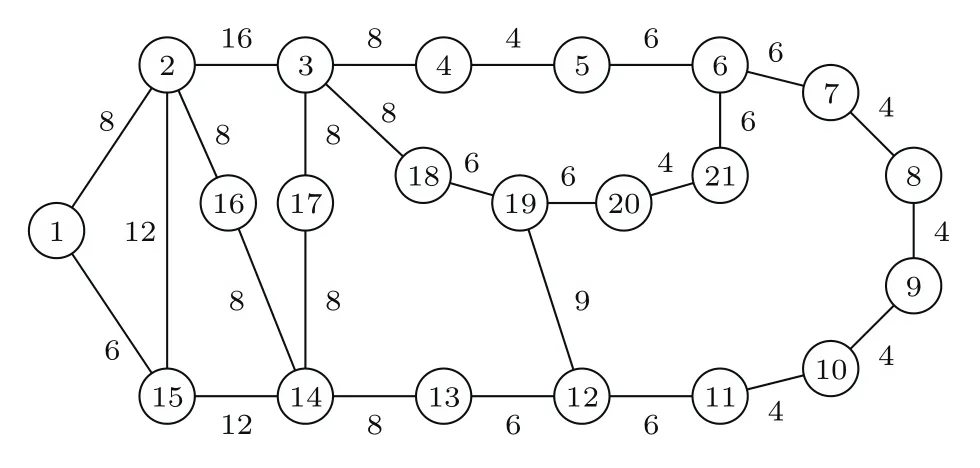
图3 无向加权ARPA图络Fig.3.Undirected weighted network obtained by the ARPA network.

图4 ARPA网络节点按基于偏离均值的方差大小排序Fig.4.Nodes in ARPA sorted by the variance from the mean deviation.

在异质网络扰动测试上,本文建立了DWS网络的异质网络动力学模型.DWS网络既含有规则的树形骨架,又含有随机的连接[30].从DWS网络反映的实际物理系统上看,层级之间有隶属关系,第一层节点只有一个,级别最高,层级越高的节点级别越低.本文假设处于树形骨架层级越低的节点,其自身动力学模型的稳定性越好,节点vi自身动力学模型的可调参数表示网络的平均度,fG(vi)表示节点vi所属的层级.本文建立了四层共100个节点的DWS网络,添加连接的算法是任意选择两个节点i和j,依概率

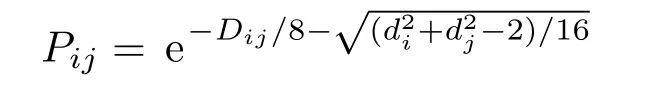
在节点vi和节点vj间添加随机的连接,其中Dij表示节点vi和节点vj最近共同上级的深度,di和dj分别表示节点vi和节点vj的深度,并且所有边的权重皆为1.通过对DWS网络中每个节点进行扰动测试,得到的节点重要性排序如图5所示.图中横坐标表示排序,纵坐标表示节点的编号,图中紫色的三条横线将所有点分为4个部分,从下往上分别对应于第一层节点、第二层节点、第三层节点和第四层节点,级别最高的第一层节点只有一个节点,第二层节点有5个,第三层节点有19个,其余的都是第四层的节点.可见级别越低的节点重要性越高,这不仅是因为级别低的节点度数小,同时也是因为级别低的节点自身动力学模型稳定性差,容易受扰动影响,这与对DWS网络进行级联失效时选择从末端节点进行打击相符[31].进一步,如果将第一层和第二层的所有节点自身动力学模型可调参数都设置为经过扰动测试得出的节点重要性排序如图6所示,与图5相比,可以发现第一层和第二层节点重要性有明显提高,并且都高于第三层节点,特别是节点1从第100位提高至第57位,节点5从第98位提高至第54位.该变化符合实际,因为在度不变的情况下节点自身稳定性与节点的重要程度负相关,即稳定性越差的节点,其重要程度越高.

图5 扰动测试条件下DWS网络节点的重要性排序Fig.5.Rank of important nodes in DWS under disturbance test.

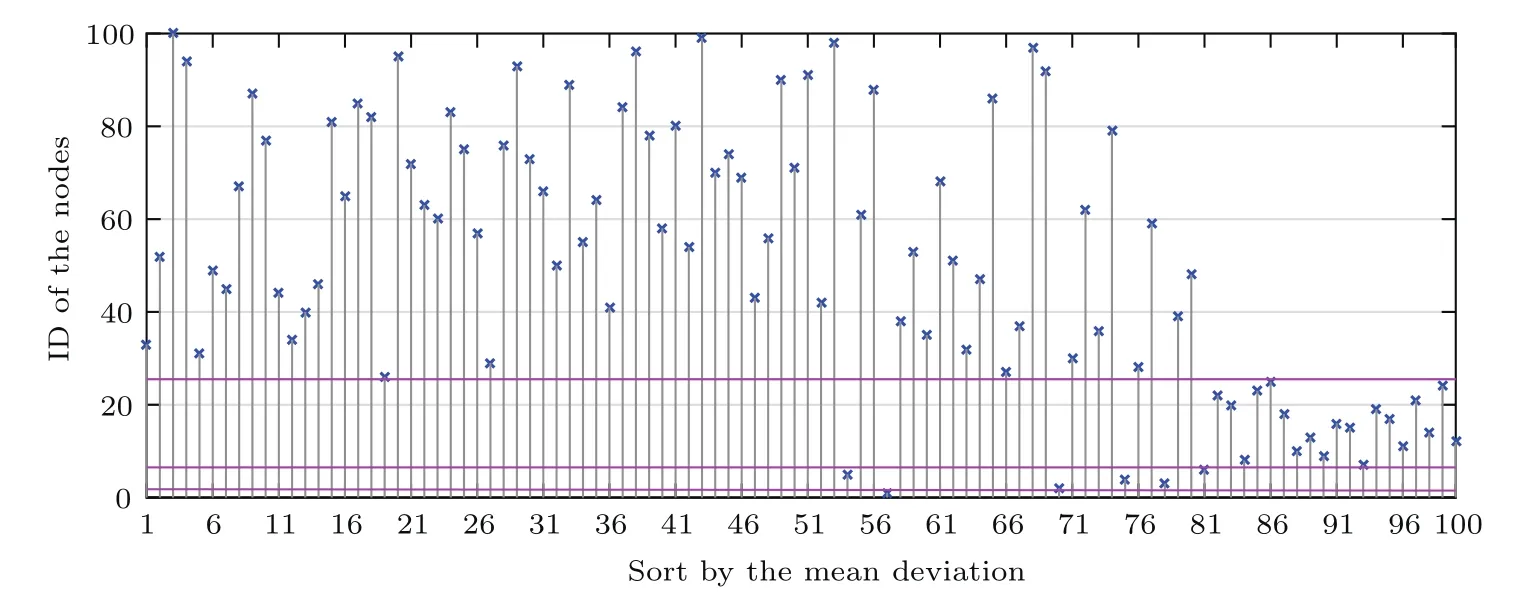
图6 扰动测试条件下调整后的DWS网络节点的重要性排序Fig.6.Rank of important nodes in adjusted DWS under disturbance test.

4.2 破坏测试的有效性分析

本节先对同质网络破坏测试方法的有效性进行验证,然后对异质网络破坏测试方法的有效性进行验证.同质网络节点自身动力学模型相同,所以同质网络破坏测试方法可以与其他基于网络拓扑结构的节点重要性方法进行对比分析,本文选用了度中心性方法、互信息方法、PageRank方法和介数中心性方法与同质网络破坏测试方法进行比较.首先在三种典型网络上进行对比验证,其分别为图3所示的ARPA网络、图7所示的对称无向加权网络[27]以及图8所示的典型社交网络——Karate俱乐部网络[32].表1—表3分别列出了在这三种网络上不同方法得到的前10个重要节点,表中括号前数值为节点编号;括号内为对应方法计算所得数值,这些数值是节点排序的依据.对于ARPA网来说,破坏性测试方法得出的前4个重要节点一定程度上是另外四种方法的综合,即和其余四种方法中的两种方法结论相同.值得注意的是,破坏性测试方法的结论与PageRank方法的结论差异最小.对于对称无向加权网络来说,破坏性测试得出的前4个重要节点也是度中心性方法、互信息方法、PageRank方法和介数中心性方法得出的前4个重要节点.对于Karate俱乐部网络来说,五种方法得出的最重要的五个重要节点基本相同,只有互信息方法得出的第4、第5重要节点的顺序和其他四种方法的不同.这三个网络上的实验表明破坏测试方法是合理有效的.此外,与另外四种方法相比,破坏性测试方法在节点重要性评估上的区分度最好,主要体现在表1中节点12和节点19,除破坏性测试方法和介数中心性方法,其余三种方法无法区分这两个节点,以及在表2中破坏性测试方法计算出的节点偏离均值完全反映出了节点对称关系,明显优于其他四种方法.

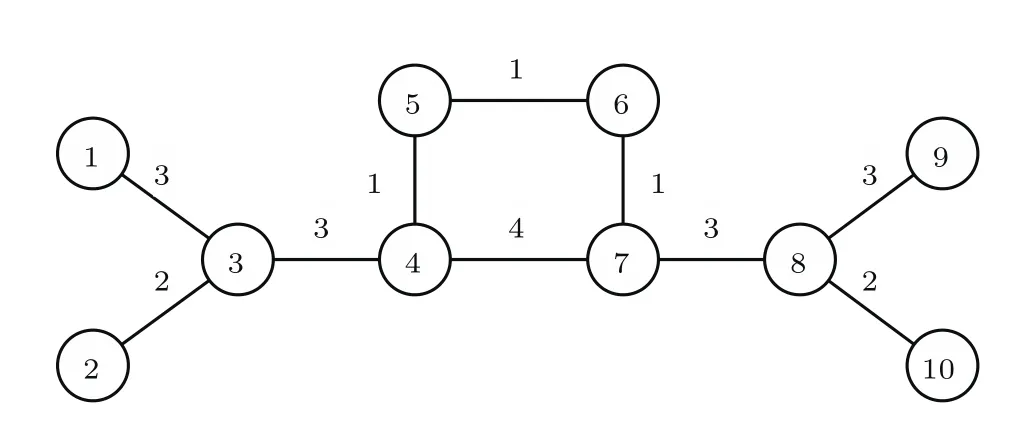
图7 对称无向加权网络Fig.7.Undirected weighted network with symmetric structure.

图8 Karate俱乐部网络Fig.8.Karate club network.

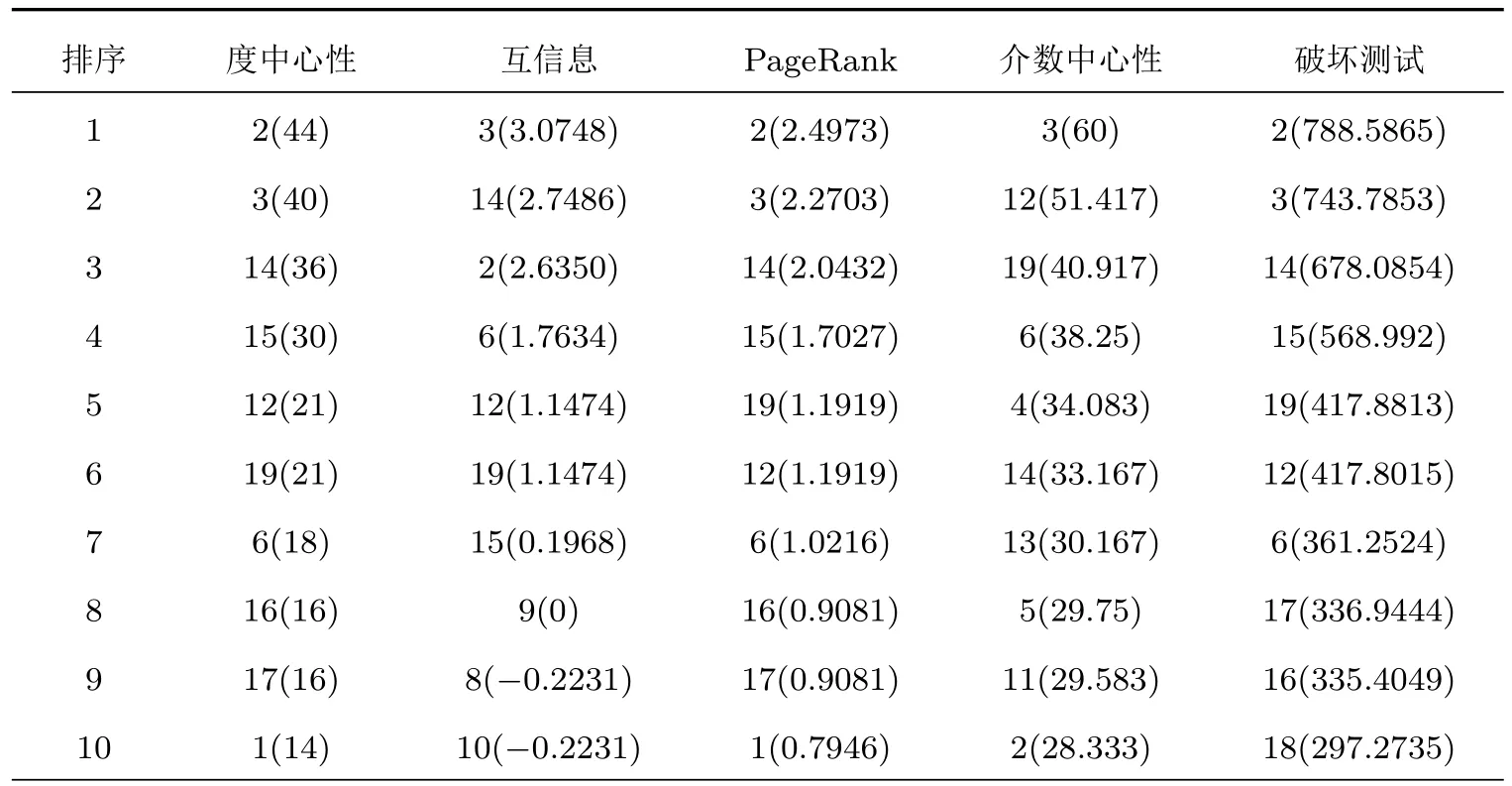
表1 无向加权ARPA网络中节点重要性排序结果Table 1.Importance ranking results of the undirected weighted ARPA network.

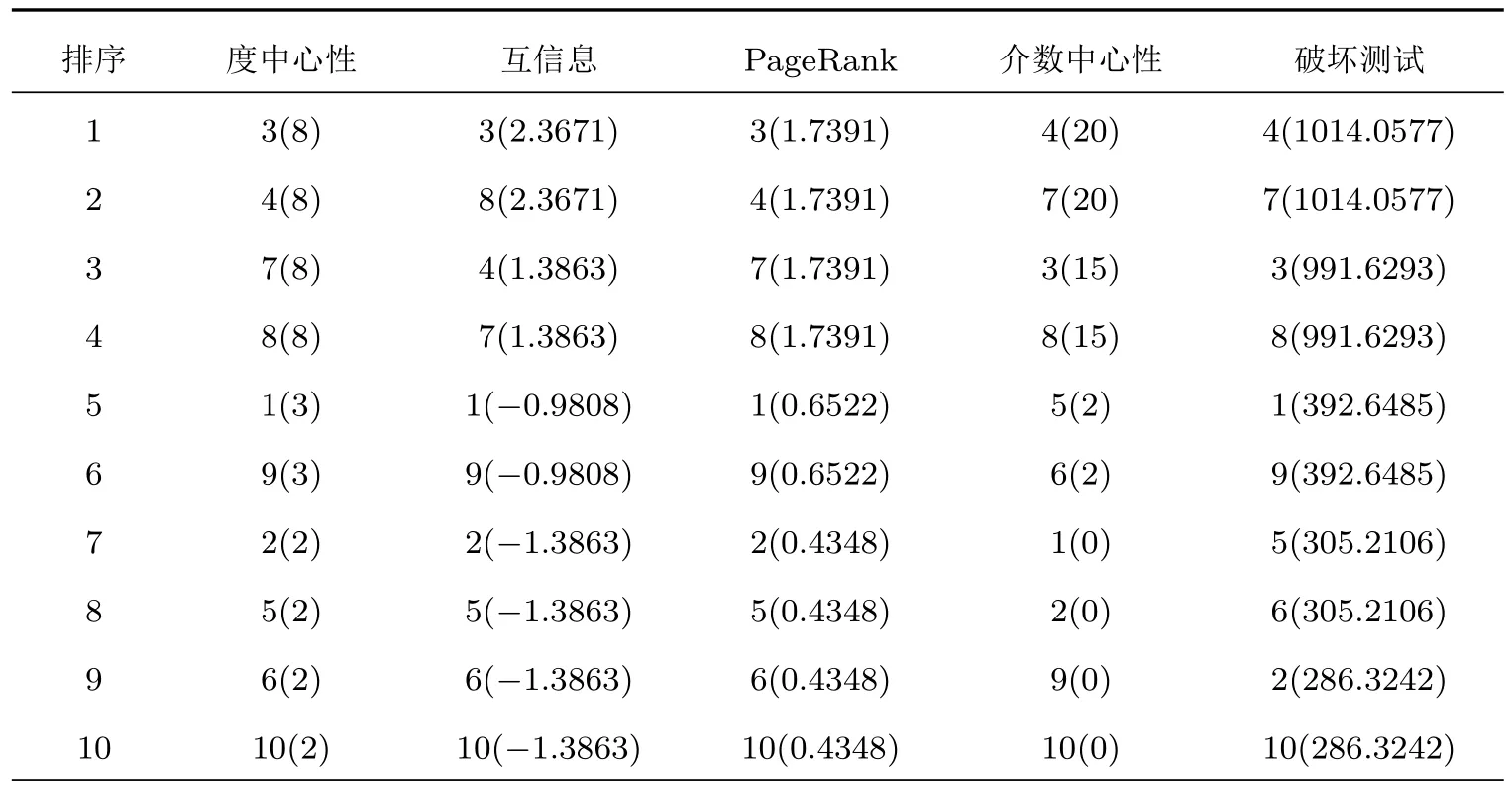
表2 图7对称网络中节点重要性排序结果Table 2.Importance ranking results of the undirected symmetric weighted network in Fig.7.

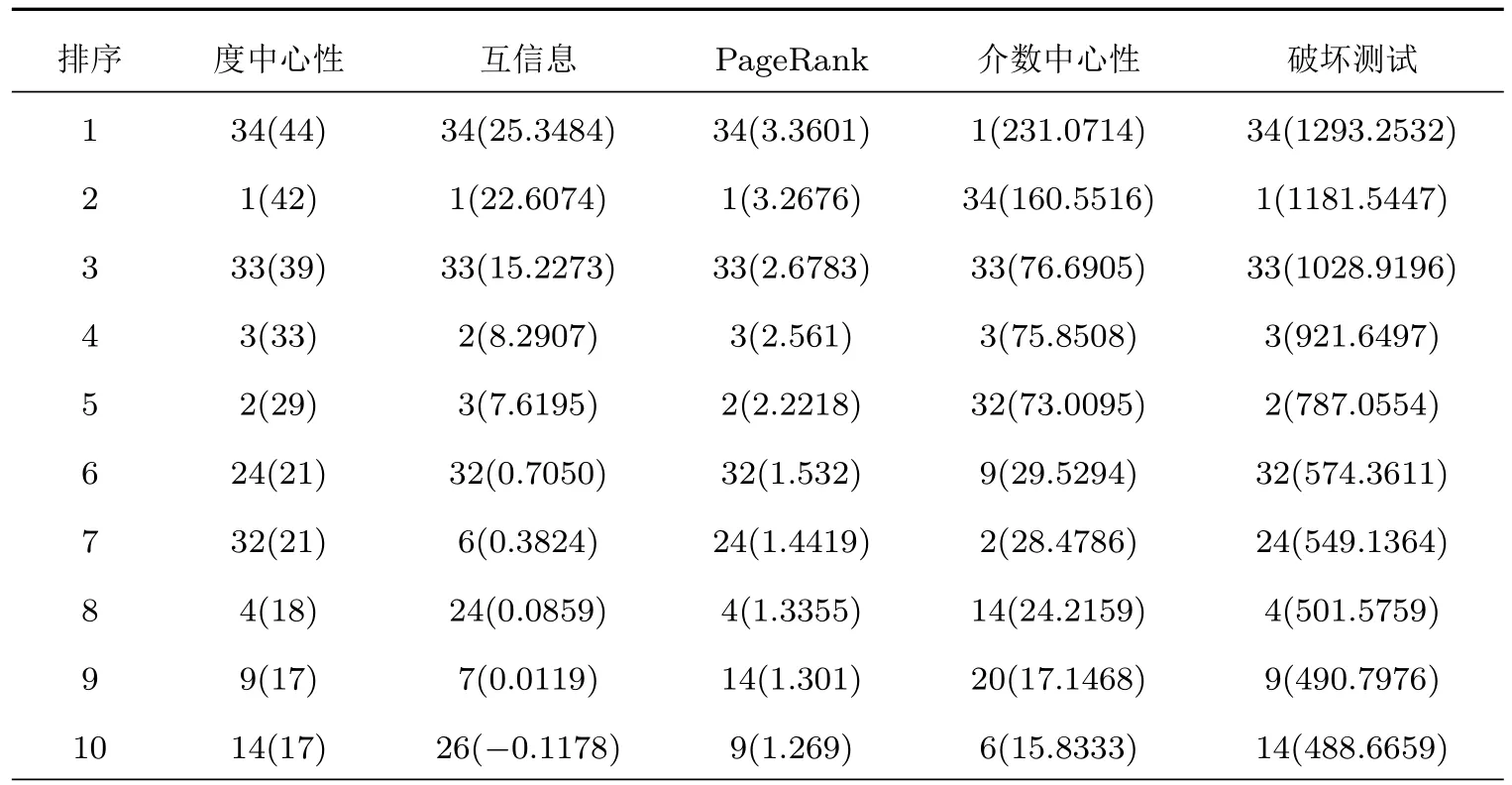
表3 加权Karate俱乐部网络中节点重要性排序结果Table 3.Importance ranking results of the Karate club network.

在实际复杂网络系统中,很多网络都是BBV(Barrat-Barthelemy-Vespignani)网络,即网络的度和节点权重都满足幂律分布.本文随机建立了七类BBV网络模型[33],它们的初始节点数为9,10,11,12,13,14,15,初始边权均为1,新增边带来的额外流量为1,每次增加1个节点新增加的边分别为9,10,11,12,13,14,15.每类模型都建立50个具体网络进行分析.本文使用网络效率下降比例指标,用于衡量移除最重要节点对网络效率的影响,具体在七类共350个随机产生的BBV网络上,利用该指标对破坏性测试方法和度中心性方法、互信息方法、PageRank方法、介数中心性方法得出的重要节点进行比较分析.网络效率下降比例可表示为[34]

其中η为节点移除后网络效率,η0为未移除节点时的网络效率.针对本文中权重越大表示联系越紧密的情况,设定相邻节点的路径为对应边权的倒数,具体的节点移除后网络效率为

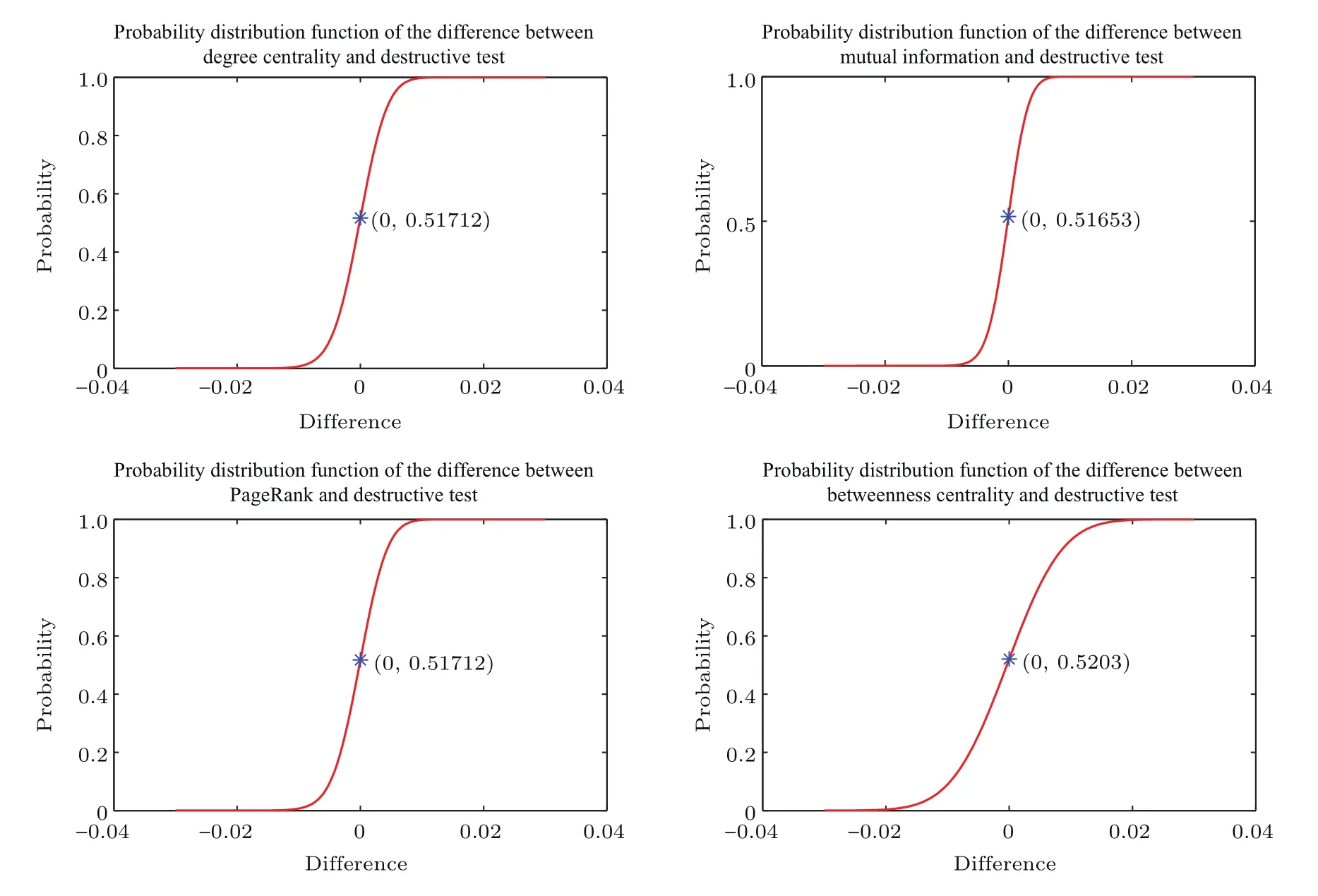
图9 新增节点与之前9个节点相连的BBV网络的效率差值分布函数Fig.9.Efficiency difference distribution function of the BBV network with every new node connected to the previous 9 nodes.

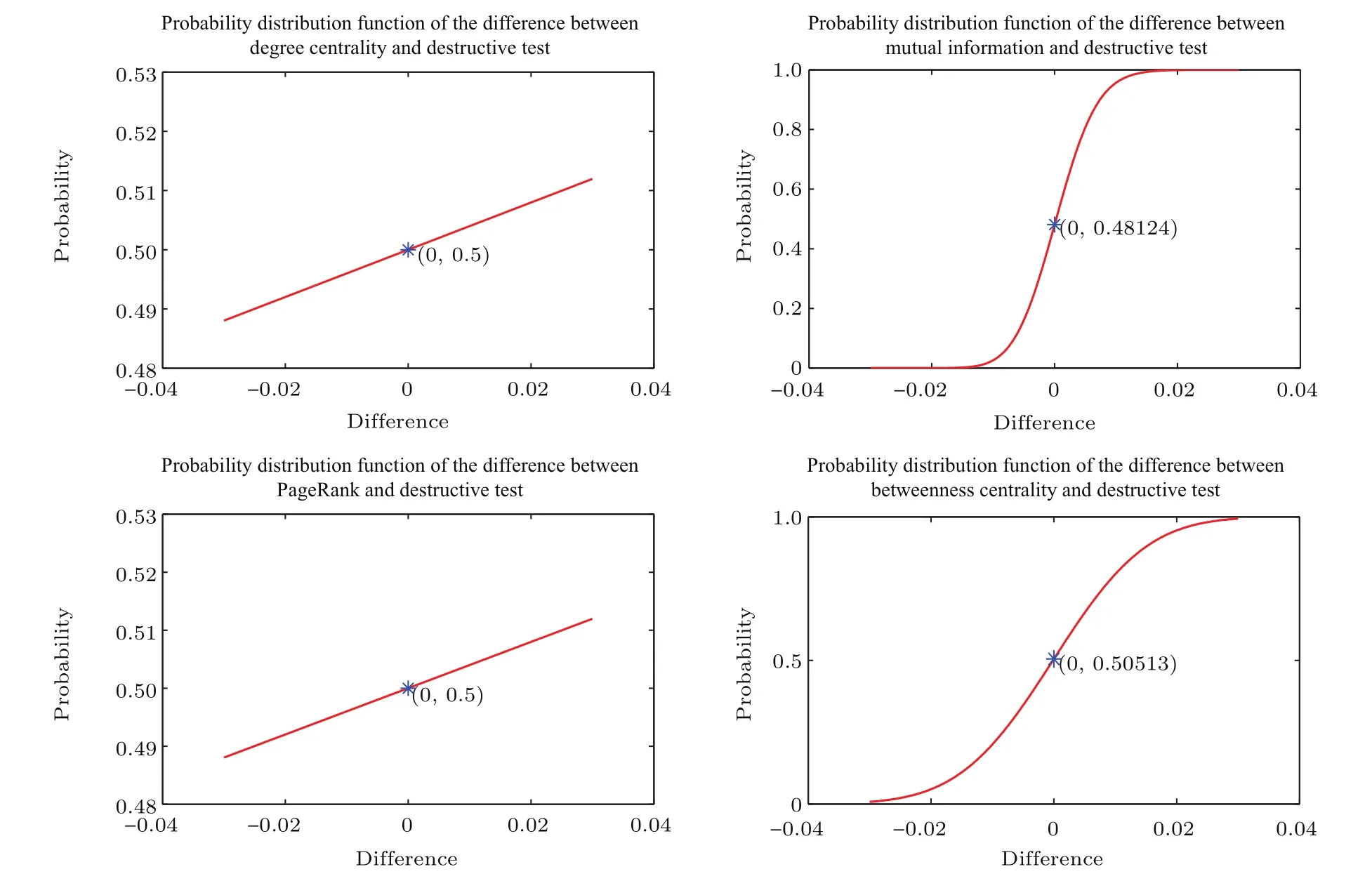
图10 新增节点与之前10个节点相连的BBV网络的效率差值分布函数Fig.10.Efficiency difference distribution function of the BBV network with every new node connected to the previous 10 nodes.

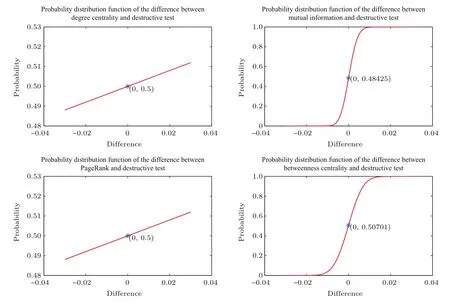
图11 新增节点与之前11个节点相连的BBV网络的效率差值分布函数Fig.11.Efficiency difference distribution function of the BBV network with every new node connected to the previous 11 nodes.

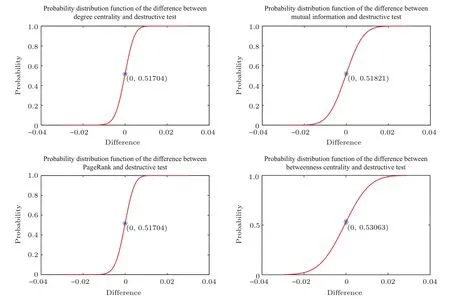
图12 新增节点与之前12个节点相连的BBV网络的效率差值分布函数Fig.12.Efficiency difference distribution function of the BBV network with every new node connected to the previous 12 nodes.

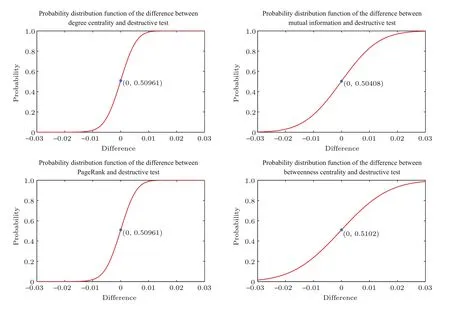
图13 新增节点与之前13个节点相连的BBV网络的效率差值分布函数Fig.13.Efficiency difference distribution function of the BBV network with every new node connected to the previous 13 nodes.

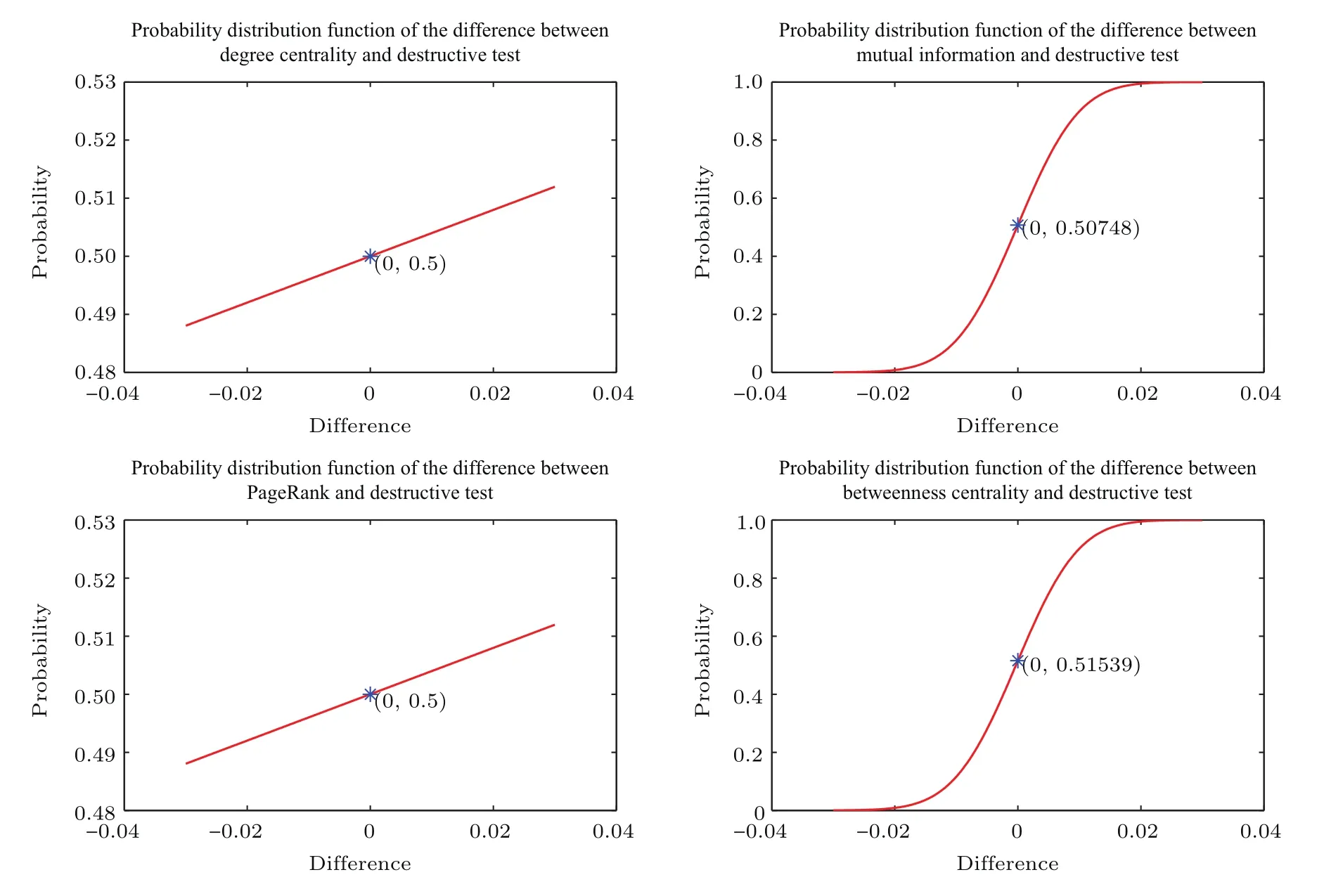
图14 新增节点与之前14个节点相连的BBV网络的效率差值分布函数Fig.14.Efficiency difference distribution function of the BBV network with every new node connected to the previous 14 nodes.

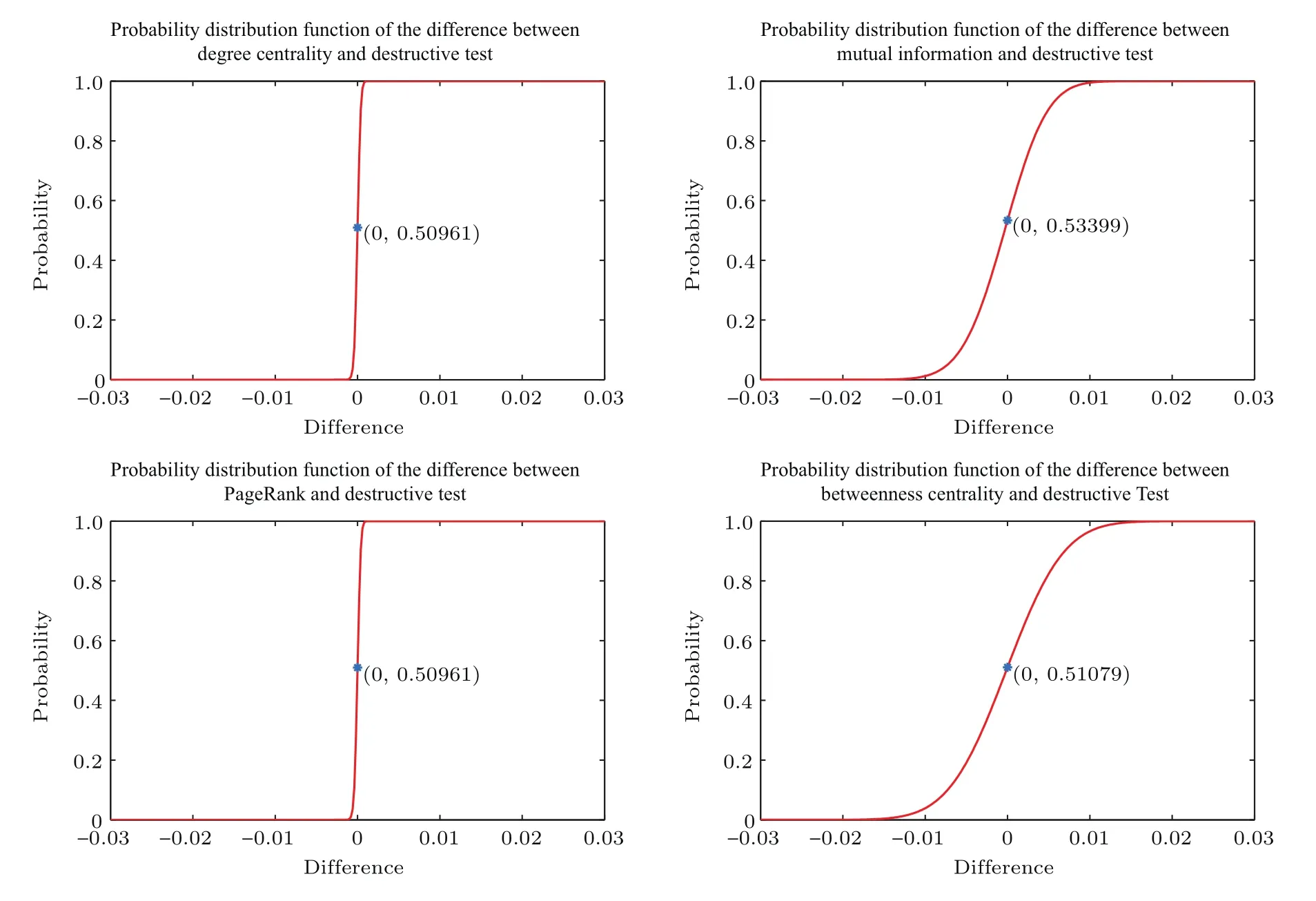
图15 新增节点与之前15个节点相连的BBV网络的效率差值分布函数Fig.15.Efficiency difference distribution function of the BBV network with every new node connected to the previous 15 nodes.

其中n为节点总数,rij为节点vi到vj的最短路径.通过从这些网络中删除最重要的节点,分析网络效率下降比例.以从网络中删除破坏测试方法得出的最重要节点后网络效率下降比例为该网络的基准值,用从对应网络中删除其他方法得出的最重要节点后网络效率下降比例减去该网络基准值得出差值,如果该差值为正,则表示其他方法得出的重要节点优于破坏测试方法.针对每类BBV网络的50个具体网络,计算出每种方法下网络效率下降比例与对应基准值的50个差值,利用核密度估计方法估计这些差值的概率分布函数,进而分析对比破坏测试方法与其他四种方法的优劣.图9—图15分别展示了每类BBV网络中其他四种方法得到的差值概率分布函数.如果图中差值为0对应的概率大于0.5,其表示差值小于0的可能性更大,也就是说删除其他方法得出的最重要节点时造成的效率下降值低于删除破坏测试方法得出的最重要节点时造成的效率下降值的可能性更大,即破坏测试方法依概率优于对应的其他方法.从图9、图12、图13和图15可以看出,破坏测试方法优于其他四种方法.从图10和图11可以看出,破坏测试方法没有互信息方法好,与度中心性方法和PageRank方法相当,比介数中心性方法好.从图14可以看出,破坏测试方法、度中心性方法和PageRank方法相当,破坏测试方法要优于互信息方法和介数中心性方法.综合以上BBV网络上的实验结果,可以得出破坏测试方法具有统计学意义上的最优性,删除其计算得出的重要节点导致网络效率下降幅度最大.

在异质网络破坏测试方法有效性验证上,本文选择在4.1节中建立的异质DWS网络模型上进行实验.通过破坏测试方法得出的节点重要性排序如图16所示,可以看出度高并且级别高的节点是比较重要的节点,这与异质网络上的扰动测试方法得出的结论相反.图16中显示节点v1比节点v20重要,并且在实验建立的DWS网络中,节点v1和节点v20的度相同.如果提高节点v20的稳定性,设置其自身动力学模型的可调参数为再次进行破坏测试,可以发现节点v20比节点v1重要,具体如图17所示.由此可见,利用异质网络破坏测试方法进行节点重要性评估,节点度越大,节点越重要,同时在控制度不变的情况下,节点自身动力学模型越稳定,节点越重要.该结论与实际相符,因为破坏度大的点影响范围大,所以重要.同时由于稳定性好的点可以更好地促进网络稳定和保持网络处于平衡状态,所以节点的重要程度与节点自身动力学模型的稳定性正相关.

图16 破坏测试条件下的DWS网络节点的重要性排序Fig.16.Rank of important nodes in DWS under destructive test.

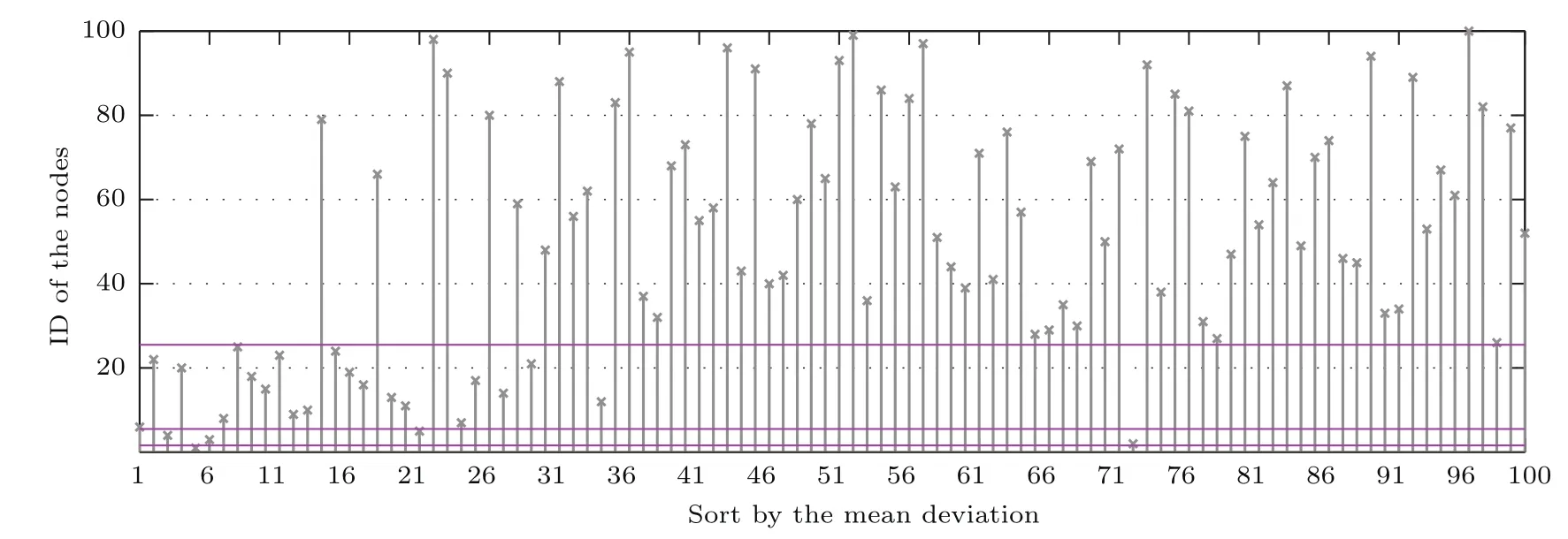
图17 破坏测试条件下调整后的DWS网络节点的重要性排序Fig.17.Rank of important nodes in adjusted DWS under destructive test.

5 结 论

分析复杂网络中的重要节点可以帮助我们有针对性地设计防护策略或者有效控制网络上危害的蔓延.现有的复杂网络的节点重要性评估方法中,从网络拓扑结构出发,建立网络局部与全局以及节点位置相关的评价指标进行节点重要性评估的研究比较成熟,但是基于复杂网络动力学模型的节点重要性评估方法较少,已有的方法多是针对给定并且满足特定条件的复杂网络动力学模型展开的.对于无向加权网络,本文提出了建立其对应动力学模型的方法,并从理论上证明了建立的动力学模型是大范围一致渐进稳定的.基于动力学模型,本文进一步提出了两种节点重要性评估方法,并揭示了现有的基于拓扑结构的和基于动力学模型的节点重要性评估方法结论的差异源于节点功能是否被破坏.扰动测试方法是在不破坏节点功能的情况下,分析对哪些节点施加干扰对网络整体平衡状态影响最大,从而确定重要节点.实验表明该方法所得结论与现有基于动力学模型的节点重要性评估方法的结论一致程度较高,即重要节点倾向于避免高度节点.破坏测试方法是节点受到破坏并且无法恢复正常时,通过比较破坏节点对网络整体平衡状态造成影响的不同来确定节点的重要性,实验表明该方法所得结论与基于网络拓扑结构的节点重要性评估方法的结论一致程度较高.特别是对BBV网络进行节点重要性评估和以网络效率为评估指标时,实验表明在统计意义上破坏测试方法得出的重要节点比度中心性方法、互信息方法、PageRank方法和介数中心性方法更为合理和稳定.由于扰动测试方法和破坏测试方法既包含了网络拓扑结构信息又包含了节点自身特性,所以本文提出的节点重要性评估方法能更加全面地反映不同节点重要性.同时,本文建立了偏离均值和基于偏离均值的方差两级评估标准,对节点重要性评估更为细致,区分度好.此外,建立异质的复杂网络动力学模型时,节点自身动力学模型的可调参数可以灵活设置,可以更好地面向实际问题建立动力学模型和进行节点重要性评估.

本文只针对单个节点的重要节点评估进行了研究,进一步可以将扰动测试方法和破坏测试方法用于重要节点集合的评估.由于是连续时间动力学模型,除衡量测试开始至系统稳定的时期内的偏离均值和基于偏离均值的方差外,还可以分析自测试开始后每个时刻的复杂网络动力学模型状态变化轨线,依据状态变化轨线设置更合理的与时间相关的节点重要性评估指标.为了建立更合理的动力学模型,可以进一步结合信息在不同节点之间传递的延时效应,建立具有延时环节的复杂网络动力学模型.同时,针对网络中的节点建立更为一般的非线性动力学方程并基于其进行节点重要性评估,具有重要研究价值.这将是我们下一步研究的方向.

参考文献

[1]Zhao M,Zhou T,Wang B H,Wang W X 2005Phys.Rev.E72 057102

[2]Zemanová L,Zhou C,Kurths J 2006Physica D224 202

[3]Lü L Y,Chen D B,Ren X L,Zhang Q M,Zhang Y C,Zhou T 2016Phys.Rep.650 1

[4]Bonacich P 1972J.Math.Sociol.2 113

[5]Estrada E,Rodríguez-Velázquez J A 2005Phys.Rev.E71 056103

[6]Kitsak M,Gallos L K,Havlin S,Liljeros F,Muchnik L,Stanley H E,Makse H A 2010Nat.Phys.6 888

[7]Lü L Y,Zhou T,Zhang Q M,Stanley H E 2016Nat.Commun.7 10168

[8]Chen D B,Lü L Y,Shang M S,Zhang Y C,Zhou T 2012Physica A391 1777

[9]Ruan Y R,Lao S Y,Wang J D,Bai L,Chen L D 2017Acta Phys.Sin.66 038902(in Chinese)[阮逸润,老松杨,王竣德,白亮,陈立栋2017物理学报66 038902]

[10]Freeman L C,Borgatti S P,White D R 1991Soc.Networks13 141

[11]Estrada E,Higham D J,Hatano N 2009Physica A388 764

[12]Li Q,Zhou T,Lü L Y,Chen D B 2014Physica A404 47

[13]Zhou Y B,Lei T,Zhou T 2011Europhys.Lett.94 48002

[14]Li P X,Ren Y Q,Xi Y M 2004Systems Eng.22 13(in Chinese)[李鹏翔,任玉晴,席酉民 2004系统工程 22 13]

[15]Gao C,Wei D J,Hu Y,Mahadevan S,Deng Y 2013Physica A392 5490

[16]Wang Y,Guo J L 2017Acta Phys.Sin.66 050201(in Chinese)[王雨,郭进利 2017物理学报 66 050201]

[17]Lü L,Zhang Y C,Chi H Y,Zhou T 2011Plos One6 e21202

[18]Yan G,Zhou T,Wang J,Fu Z Q,Wang B 2005Chin.Phys.Lett.22 510

[19]Brummitt C D,D’Souza R M,Leicht E A 2012Proceedings of the National Academy of Sciences of the United States of America109 E680

[20]Du W J,Yu J L,An X L,Ma C X 2015Transport Research1 14(in Chinese)[杜文举,俞建宁,安新磊,马昌喜2015交通运输研究1 14]

[21]Liu Y Y,Slotine J J,Barabasi A L 2011Nature473 167

[22]Jia T,Barabási A L 2013Sci.Rep.3 2354

[23]Chen T P,Lu W L 2013Theory of Coordination in Complex Networks(Beijing:Higher Education Press)p14(in Chinese)[陈天平,卢文联2013复杂网络协调性理论(北京:高等教育出版社)第14页]

[24]Wang E F,Shi S M 2005Advanced Algebra(3rd Ed.)(Beijing:Higher Education Press)p160(in Chinese)[王萼芳,石生明 2005高等代数第三版 (北京:高等教育出版社)第160页]

[25]Zhong Q H 2004Modern Control Theory2004(Beijing:Higher Education Press)p142(in Chinese)[钟秋海2004现代控制理论(北京:高等教育出版社)第142页]

[26]Liang H L 2015Ph.D.Dissertation(Shanghai:Shanghai Jiao Tong University)(in Chinese)[梁海丽 2015博士学位论文(上海:上海交通大学)]

[27]Wang B,Ma R N,Wang G,Chen B 2015J.Comput.Appl.35 1820(in Chinese)[王班,马润年,王刚,陈波2015计算机应用35 1820]

[28]Brin S,Page L 1998Computer Networks and ISDN Systems30 107

[29]Yao Z Q,Shang K K,Xu X K 2012J.Univ.Shanghai Sci.Technol.34 18(in Chinese)[姚尊强,尚可可,许小可2012上海理工大学学报34 18]

[30]Dodds P S,Watts D J,Sabel C F 2003PNAS100 12516

[31]Yuan M 2014Acta Phys.Sin.63 220501(in Chinese)[袁铭2014物理学报 63 220501]

[32]Zachary W W 1977J.Anthropol.Res.33 452

[33]Pan Z F,Wang X F 2006Acta Phys.Sin.55 4058(in Chinese)[潘灶烽,汪小帆 2006物理学报 55 4058]

[34]Latora V,Marchiori M 2007New J.Phys.9 188