基于两级压缩感知的脉冲星时延估计方法∗
康志伟 吴春艳 刘劲 马辛 桂明臻
1)(湖南大学信息科学与工程学院,长沙 410082)
2)(武汉科技大学信息科学与工程学院,武汉 430081)
3)(北京航空航天大学仪器科学与光电工程学院,北京 100191)
1 引 言
X射线脉冲星导航作为一种前瞻性的航天器自主天文导航方法,能为近地轨道、深空和星际飞行的航天器提供位置、速度、时间、姿态等丰富的导航信息[1,2].天文台通过长期的天文观测,可获得高信噪比的脉冲星标准脉冲轮廓,器载X射线探测器通过短时间观测采集X射线脉冲星信号,并将这些信号按照周期累积,可得到脉冲星累积脉冲轮廓,其信噪比较低.X射线脉冲星导航的基本量测量是脉冲时延,它通过比较脉冲星累积脉冲轮廓相对于标准脉冲轮廓的相位得到[3,4].如何快速精确地进行累积脉冲轮廓时延估计是提高脉冲星自主导航性能的关键[5].
脉冲星累积脉冲轮廓的时延估计方法主要分为频域与时域两类[6−9].频域方法所需的变换、计算相对复杂,而时域方法较为直观、计算量小、实时性较好,已得到研究者关注.Emadzadeh和Speyer[10]提出了在时域利用历元折叠得到累积脉冲轮廓后,再通过设计累积脉冲轮廓与标准脉冲轮廓的最小二乘目标函数,以获得相位值的时延估计方法.另外,Emadzadeh和Speyer[11]还提出了利用累积脉冲轮廓与标准脉冲轮廓间的互相关函数的最大值来估计时延.李建勋和柯熙政[12]提出了利用到达时间概率函数构建最大似然准则对脉冲星累积脉冲轮廓进行时延估计的方法.
压缩感知[13]是一种时域的信号处理方法,它基于信号的稀疏性,通过极低的采样率获取的信息来重构原始信号,近年来已被应用于累积脉冲轮廓时延估计.苏哲等[14]提出了一种基于模信转换器的观测矩阵,以构建能在短时间内得到高信噪比累积脉冲轮廓的压缩感知方法.Li等[15]将脉冲探测过程模拟成对累积脉冲轮廓的随机采样,以随机0-1矩阵作为测量矩阵实现了一种能有效提高实时性的压缩感知方法.Shen等[16]利用Hadamard矩阵正交性好以及其元素为−1与+1时容易硬件实现和易存储的特点,提出了一种基于Hadamard测量矩阵的累积脉冲轮廓压缩感知方法.
以上累积脉冲轮廓时延估计主要是基于测量矩阵及其改进的压缩感知方法,具有较好的时延估计性能.考虑到压缩感知方法中字典的原子数与字典精度密切相关,原子个数越多则原子间隔越小、估计越精确,但相应的计算量也越大.因此,从波形字典的角度来考虑,实现具有高精度、低计算复杂度的压缩感知累积脉冲轮廓时延估计方法是一条值得探讨的途径.
针对传统字典中原子数增加虽可提高估计精度但会增加计算量这一问题,本文基于波形字典的可分解性,构建粗估计与精估计两级字典,探寻运用两级字典压缩感知的脉冲星累积脉冲轮廓时延估计方法,以实现能进行全局估计与局部估计的动态组合,达到具有高精度和低计算复杂度的时延估计性能.
2 X射线脉冲星信号轮廓模型
X射线脉冲星信号轮廓是通过长时间天文观测获取脉冲星辐射数据,并对其进行脉冲周期折叠和同步平均而得到,其本质是探测到的光子流量密度与相位或时间的曲线关系[2].脉冲星标准脉冲轮廓是一组具有超高信噪比的数据,累积脉冲轮廓是在某一观测时间段累积得出的数据.假设观测时间间隔为(u0,uf),总的观测时间为Tobs=uf−u0,定义ui为第i个光子的到达时间,递增的到达时间集合{u1,u2,···,uM}可表示成u06u16u26···6uM6uf,设u0=0,Cu为(0,uf)时间间隔内探测到的光子数量,它是具有时变速率λ(u)>0的非齐次泊松过程.对于固定的时间uf,Cu是泊松过程的随机变量,在时间间隔(0,u)内探测到m个光子的概率可表示为[11]

其均值和方差分别为

标准脉冲轮廓模型,即总流量密度函数λ(u),由X射线脉冲星的光子密度及来自背景环境的光子密度构成:
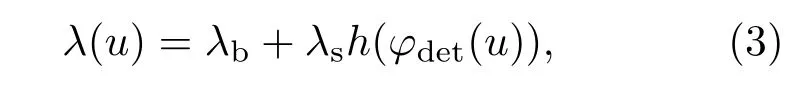
式中λb和λs分别代表已知有效的背景流量和脉冲星源的流量;h(φ)为归一化周期脉冲轮廓,具有以下特性[17]:minφh(φ)=0,φ∈[0,1);φdet(u)为探测器相位.
对于同一颗脉冲星,累积脉冲轮廓与标准脉冲轮廓的关系可表示如下[2]:
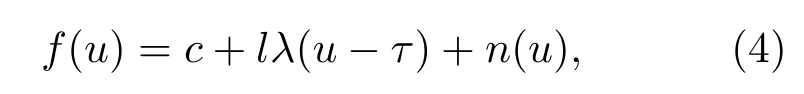
式中f(u)为累积脉冲轮廓,λ(u)为标准脉冲轮廓,n(u)为噪声,c为直流分量,l为放大系数,τ为累积脉冲轮廓相对于标准脉冲轮廓的时间延迟值.
实际提取出的脉冲星标准脉冲轮廓与累积脉冲轮廓是离散序列.标准脉冲轮廓在一个周期P中有N个采样点,每个采样点的间隔为∆t=P/N,则累积脉冲轮廓与标准脉冲轮廓关系为
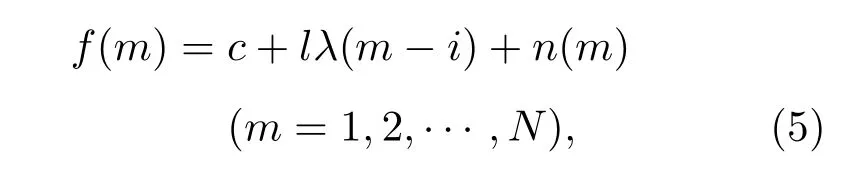
i为累积脉冲轮廓相对于标准脉冲轮廓的延迟间隔数,脉冲时延估计量为
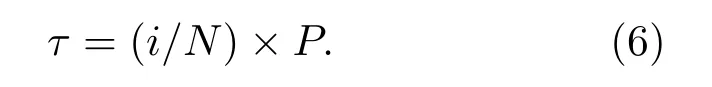
3 两级压缩感知的时延估计算法
压缩感知作为一种新采样理论,利用了信号的稀疏性,在低采样率的情况下,通过降维来获取信号的离散样本以重建信号.压缩感知主要包括三个部分:信号的稀疏表示、测量矩阵采样和信号重构.
压缩感知以其低计算复杂度与累积时间短而优于其他方法,近年来已被用于脉冲星时延估计.字典是一个影响压缩感知估计精度的重要因素.字典中原子数越多,估计精度越高,但同时也增加了计算复杂度.为此,本文采用两级字典使其在提高估计精度的同时降低计算复杂度.两级字典包括粗估计字典与精估计字典,粗估计字典原子间隔大,能提供全相位估计,精估计字典原子间隔小,且个数少,能提供局部估计.利用粗估计字典对累积脉冲轮廓时延值进行预估计,将其相位调整到精估计字典的估计范围内,再利用精估计字典得到精确时延值.
3.1 两级字典的脉冲轮廓稀疏表示
字典选择在压缩感知稀疏过程中起着至关重要的作用,由(4)式可知,累积脉冲轮廓和标准轮廓经归一化后,仅相差一个时间延迟量.因此,对X射线脉冲轮廓,可根据标准脉冲轮廓λ(u)设计出粗估计与精估计两级字典.
第一级由粗估计字典提供全局相位预估计.粗估计字典包含脉冲轮廓的所有相位,采样点数越多、字典原子间隔越小、时延估计值越精确,但这种全局估计会增加计算量.因此,第一级可先采用子间隔大的粗估计字典对时延值进行预估计,以减少计算量.粗估计字典ΨR[14,18]设计为N1×N1维:
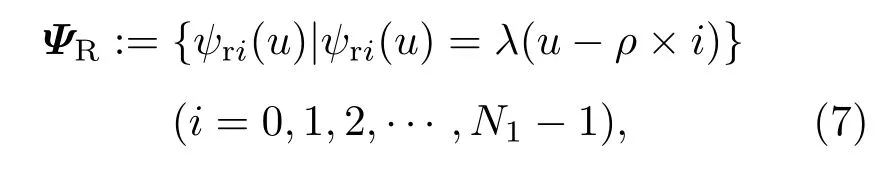
式中ΨR为粗估计字典;ψri(u)为字典中第i个原子;N1为第一级输入信号长度即字典原子个数;ρ为累积脉冲信号与第一级输入信号的长度比,ρ=N/N1,其中N为累积脉冲信号长度,N1
第二级由精估计字典提供对时延值的局部精确估计.精估计字典只包含部分相位的原子,其数量少、子间隔小,从而减小了字典尺寸、降低了计算量.精估计字典矩阵ΨP为N×D维,其数据量仅为传统字典的D/N,即使原子个数远小于信号长度,也可对时延值进行局部精确估计.精估计字典表示如下:

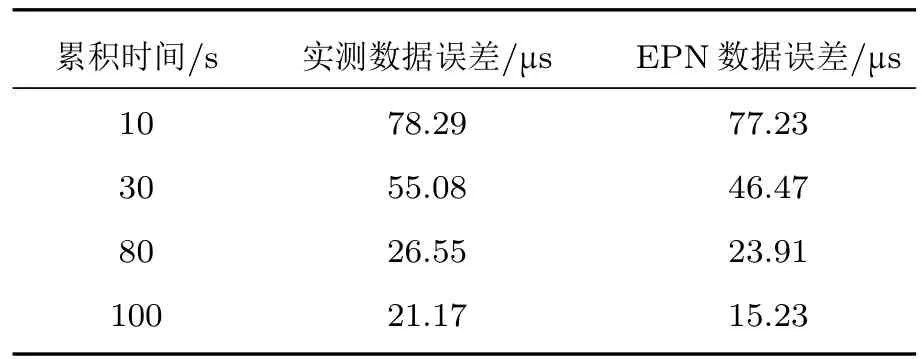
式中,ΨP为精估计字典;ψpj(u)为第j个原子;N为信号长度;D为字典原子个数,D 累积脉冲轮廓可由字典原子与稀疏系数表示为 式中,fR(u)是粗估计累积脉冲轮廓,ai是粗估计字典中第i个原子对应的稀疏系数,fP(u)是精估计累积脉冲轮廓,aj是精估计字典中第j个原子的稀疏系数. 测量矩阵的选取对数据采样和信号重构十分重要.由于信号在相同稀疏阶次情况下,哈达玛矩阵的恢复效果优于随机0-1矩阵[16],本文选择哈达玛矩阵作为测量矩阵.测量矩阵采样是一个降维的过程,第一级中可选取哈达玛矩阵的前M1行,表示如下[15]: 式中ΦR是粗估计测量矩阵;H为哈达玛矩阵,矩阵,用于选取哈达玛矩阵的前M1行;yR是测量值;fR为第一级输入信号;ΘR为感知矩阵;AR是一阶稀疏系数矩阵,AR={a1,a2,a3,···,aN1−1}. 第二级精估计测量矩阵为 其中,ΦP是精估计测量矩阵; 为M2×N矩阵,其中M2=Sa2×N,Sa2为第二级信号采样率;fP第二级输入信号;ΘP为感知矩阵. 累积脉冲轮廓的重构是一阶稀疏信号的优化问题,可选择正交匹配追踪法[19]进行累积脉冲轮廓重构.时延估计由粗估计与精估计两级构成,图1为两级时延估计算法流程图. 第一级粗估计与重构算法如下: 1)初始化残差r0=yR,迭代选取的位置Λ1=φ,增量矩阵T1=φ,初始迭代次数i=1; 2)寻找感知矩阵中与残差投影系数最大,即内积最大的列原子向量,保存最大投影系数对应的位置保存对应的列原子向量Ti=Ti−1∪θt; 3)求yR=Ti·ai的最小二乘解i; 4)输出稀疏系数A,利用等式fR=ΨRA进行信号重构. 图1 两级时延估计算法流程图Fig.1.Flow chart of two stage delay estimation algorithm. 第一级输出索引值为t,即累脉冲轮廓相对于标准脉冲轮廓的延迟间隔数,可得预估时延值为τ1=t×ρ(µs),ρ为第二级与第一级输入信号的比值.精确时延估计值可通过第二级得到.第二级精估计字典为N×D维,只包含标准脉冲轮廓的部分相位,因此,需利用预估时延值τ1的先验条件,使累积脉冲轮廓f(u)处于精估计字典包含的相位范围内,即将其移位到精估计字典中间位置D/2,移位值为∆=(D/2)−τ1,移位修正后的输入信号为fP(u)=f(u−∆),再进行第二级精确时延估计. 第二级精估计算法如下: 1)初始化残差r0=yP,迭代选取的位置Λ1=φ,增量矩阵T1=φ,初始迭代次数i=1; 2)寻找感知矩阵中与残差投影系数最大,即内积最大的列原子向量,保留最大投影系数对应的位置保存其对应的列原子向量Ti=Ti−1∪θt1. 上述步骤得出的t1为精估计索引值,最后可得到精确时延估计值τ=(t×ρ+t1−D/2)×1(µs). 在压缩感知中,波形字典大小对时延估计精度影响很大. 在信号长度为N,且采样率为M/N的情况下,如使用一级压缩感知方法,当输入信号长度N=32768,字典原子间隔为1µs时,波形字典应为N×N维,即32768×32768.字典需占用较大内存,且运行时间长. 而采用本文方法,一级字典仅为N1×N1维,即1024×1024,二级字典为N×D维,即32768×300,二者所占存储空间比一级字典小两个数量级. 因此,本文方法能有效提高测量精度且兼顾合理的运行时间与内存. 使用欧洲脉冲星网络数据库(European Pulsar Network,EPN)数据[20]与硬X射线探测卫星(Rossi X-ray Timing Explorer,RXTE)实测数据[21]对本文方法进行了仿真实验.EPN收集了超过1000颗脉冲星的脉冲轮廓;RXTE是美国NASA发射的具有高时间分辨率、高灵敏度、宽能谱范围的大型硬X射线探测卫星,用于接收脉冲星光子以获得实测数据. 利用EPN数据获得标准脉冲轮廓,累积脉冲轮廓由泊松分布产生,以PSR B0531+21脉冲星作为导航星,对本文方法进行了轮廓重构、采样率选择、时延估计精度的仿真实验.另外,通过RXTE获取的脉冲星B0531+21的光子到达时刻进行不同时段的历元折叠,以得到标准脉冲轮廓与累积脉冲轮廓,并在不同累积时间下与基于EPN数据的时延估计精度进行对比. 有关参数为:脉冲星B0531+21的周期P=0.0334 s,背景流量为λb=5×10−3ph/(s·cm2),来自脉冲星的源流量为λs=1.54 ph/(s·cm2),X射线探测器有效面积设为800 cm2.为验证本文方法的实时性,将其在酷睿i5 CPU 2.1G计算机上进行了仿真. 为验证本文方法在重构脉冲轮廓方面的有效性,将两级压缩感知与历元折叠方法获得的脉冲轮廓信噪比进行比较. 仿真实验中,累积脉冲轮廓的子间隔数为N=32768,第一级粗估计字典为N1×N1维,测量矩阵为M1×N1维,N1=1024,M1=614,N1×N1,采样率Sa1为M1/N1=0.6;第二级精估计字典为N2×D维,测量矩阵为M2×N2维,N2=N=32768,M2=1024,D=300,采样率Sa2为M2/N2=0.03125.针对脉冲星B0531+21在不同累积时间下的脉冲轮廓的实验结果如图2所示. 图2 不同累积时间下的重构轮廓 (a)累积时间1 s;(b)累积时间10 s;(c)累积时间100 sFig.2.Reconstructed pro filesat different integrated time:(a)Integrated time of 1 s;(b)integrated time of 10 s;(c)integrated time of 100 s. 图2(a)—(c)分别给出了累积时间为1,10,100 s的历元折叠法与本文方法提供的累积脉冲轮廓.由图2可知,观测时间较短时,压缩感知恢复出的累积脉冲轮廓信噪比远高于历元折叠法的结果.因此,两级压缩感知方法能重构出高信噪比的累积脉冲轮廓. 测量矩阵采样点数与计算量以及存储空间密切相关.当测量矩阵采样点数少时,计算量较小,时延估计精度低;反之,计算量大,时延估计精度高. 针对脉冲星B0531+21在不同采样率下的时延估计精度的仿真实验中,第一级实验参数与4.1.1节一致,第二级精估计字典尺寸也与4.1.1节相同,第二级测量矩阵大小为M2×N2维,其中,N2=N=32768,M2为采样点数,分别有M2=512,1024,2048,4096,对应的采样率Sa2为M2/N2=0.015625,0.03125,0.0625,0.125. 图3(a)和图3(b)分别给出了累积时间为10—100 s,500—2500 s两个较短与较长时间内不同采样率的估计误差值,不同采样率下的运行时间如表1所列. 图3 不同时间与采样率下的时延估计精度 (a)累积时间10—100 s;(b)累积时间500—2500 sFig.3.Time delay estimation accuracy at different time and sampling rates:(a)Integrated time of 10–100 s;(b)integrated time of 500–2500 s. 表1 不同采样率下的运行时间Table 1.Running time with different sampling rates. 由图3与表1可知:采样率为0.03125对应的第二级采样点数M2=1024,采样率大于0.03125时,时延估计误差缓慢减小,运行时间明显增大,因此当累积时间大于40 s,选择0.03125为最优的采样率;但累积时间小于40 s时,不同采样率下的估计误差波动较大,因此当累积时间较短时,有必要增大采样率,选择采样率为0.125. 图4给出了脉冲星B0531+21在本文方法与一级压缩感知方法下的估计精度比较结果.本文方法下字典与测量矩阵参数与实验4.1.1节一致,一级压缩感知方法下累积脉冲轮廓的子间隔数为N=1024,第一级字典为N×N维,测量矩阵为M×N维,M=614,采样率Sa为M/N=0.6.由图4可知,在时延估计精度上,基于两级字典的压缩感知方法优于一级压缩感知.随着累积时间的延长,时延估计精度显著增加. 图4 一级与两级压缩感知估计精度的比较Fig.4.Comparison of time delay estimation between onelevel compressed sensing and two-level compressed sensing. 为进一步验证本文时延估计方法的性能,利用RXTE卫星收集到的实测数据进了仿真实验.采用RXTE中Crab脉冲星观测数据,数据包为40805-01-05-000[21],计算不同累积时间下的信号时延估计精度. 标准脉冲轮廓由数据包的光子到达时间序列经过历元折叠获得,截取数据包的一段光子到达时间序列数据,对其中所有数据加上10µs的时延,再利用新生成的时间序列进行历元折叠,即可获得具有确定时延的累积脉冲轮廓.不同累积时间的累积脉冲轮廓可通过截取数据包中不同时段的数据进行处理. 实验中,第一级粗估计字典为N1×N1维,测量矩阵为M1×N1维,N1=1024,M1=614;第二级精估计字典为N2×D维,测量矩阵为M2×N2维,N2=N=32768,M2=512,其中D=300. 实验结果列于表2,由表2可知,累积时间分别为10,30,80,100 s时,随着累积时间的增加,RXTE实测数据得到的时延估计精度与EPN数据得到的时延估计精度都有所提高,二者的误差值比较接近,这进一步表明了本文方法的有效性. 表2 RXTE实测数据与EPN数据的时延估计对比Table 2.Comparison of time delay estimation between RXTE real data and EPN data. 基于两级压缩感知的脉冲星累积轮廓时延估计是一种能保持高估计精度并降低计算量的有效方法.将字典分解为粗估计字典与精估计字典,可避免大数据量的计算,既能利用粗估计字典进行预估得到全局累积脉冲轮廓时延值,又可利用精估计字典对经过预估时延值调整的累积脉冲轮廓进行精确估计,从而实现了全局估计与局部估计的有机结合.实验结果表明,该方法能保持对累积脉冲轮廓的高估计精度,并大幅降低计算量. 参考文献 [1]Hanson J E 1996Ph.D.Dissertation(Stanford:Stanford University) [2]Sheikh S I 2005Ph.D.Dissertation(Maryland:University of Maryland) [3]Liu J,Wu J,Xiong L,Fang J C,Liu G 2017Chin.J.Electron6 1325 [4]Taylor J H 1992Philos.T.R.Soc.A341 117 [5]Tran N D,Renaux A,Boyer R,Marcos S 2014IEEE Trans.Aeros.Elec.Sys.50 786 [6]Kang Z W,He X,Liu J 2016Optik127 5050 [7]Zhang H,Xu L P,Xie Q,Luo N 2011Acta Phys.Sin.60 049701(in Chinese)[张华,许录平,谢强,罗楠2011物理学报60 049701] [8]Fang H Y,Liu B,Li X P,Sun H F,Xue M F,Shen L R,Zhu J P 2016Acta Phys.Sin.65 119701(in Chinese)[方海燕,刘兵,李小平,孙海峰,薛梦凡,沈利荣,朱金鹏2016物理学报65 119701] [9]Liu J,Fang J C,Wu J,Kang Z W,Ning X L 2014IET Radar Sonar Navig8 1154 [10]Emadzadeh A A,Speyer J L 2011IEEE Trans.Aeros.Elec.Sys.47 2317 [11]Emadzadeh A A,Speyer J L 2010IEEE Trans.Sig.Proc.58 4484 [12]Li J X,Ke X Z 2010Acta Astronom.Sin.51 263(in Chinese)[李建勋,柯熙政 2010天文学报 51 263] [13]Do T T,Gan L,Nguyen N H,Tran T D 2012IEEE Trans.Sig.Proc.60 139 [14]Su Z,Xu L P,Gan W 2011Sci.Sin.:Phys.Mech.Astron.41 681(in Chinese)[苏哲,许录平,甘伟 2011中国科学:物理学力学天文学41 681] [15]Li S L,Liu K,Xiao L L 2014Optik125 1875 [16]Shen L R,Li X P,Sun H F,Fang H Y,Xue M F 2016Optik127 4379 [17]Golshan A R,Sheikh S I 2007Annual Meeting of Institute of NavigationCambrige,MA,USA,April 23–25,2007 p413 [18]Shi G,Lin J,Chen X Y,Qi F,Liu D H,Zhang L 2008IEEE Trans.Sig.Proc.55 379 [19]Tropp J A,Gilbert A C 2007IEEE Trans.Sig.Proc.53 4655 [20]EPN http://www jb man acuk/∼pulsar/Resources/epn/browser html[2017-1-13] [21]RXTE https://heasarcnasagov/docs/archivehtml[2017-5-24]
3.2 测量矩阵选取
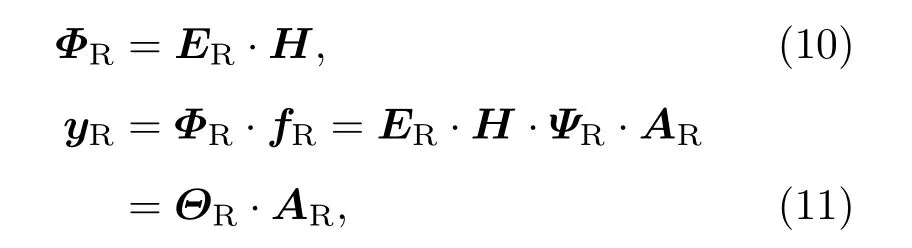
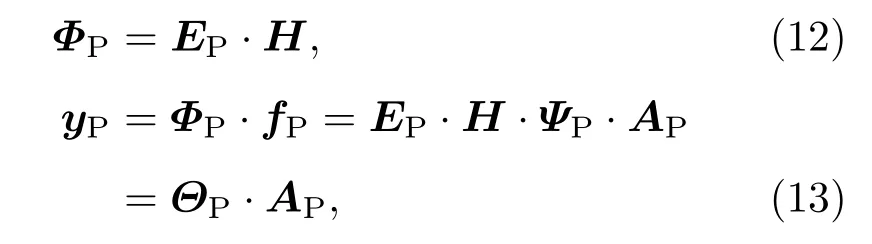
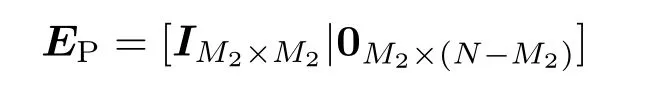
3.3 脉冲轮廓重构与时延估计算法
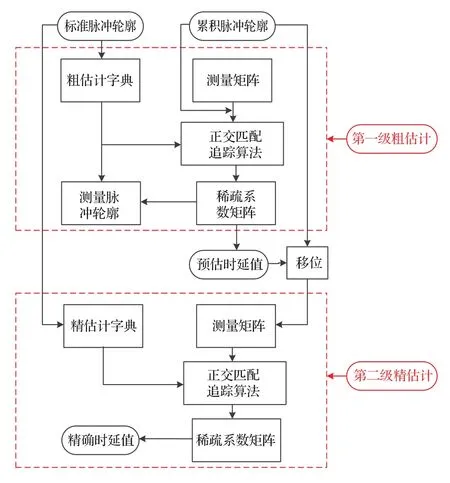
3.4 计算复杂度分析
4 仿真实验与结果分析
4.1 基于EPN数据的仿真实验
4.1.1 不同累积时间下的重构轮廓
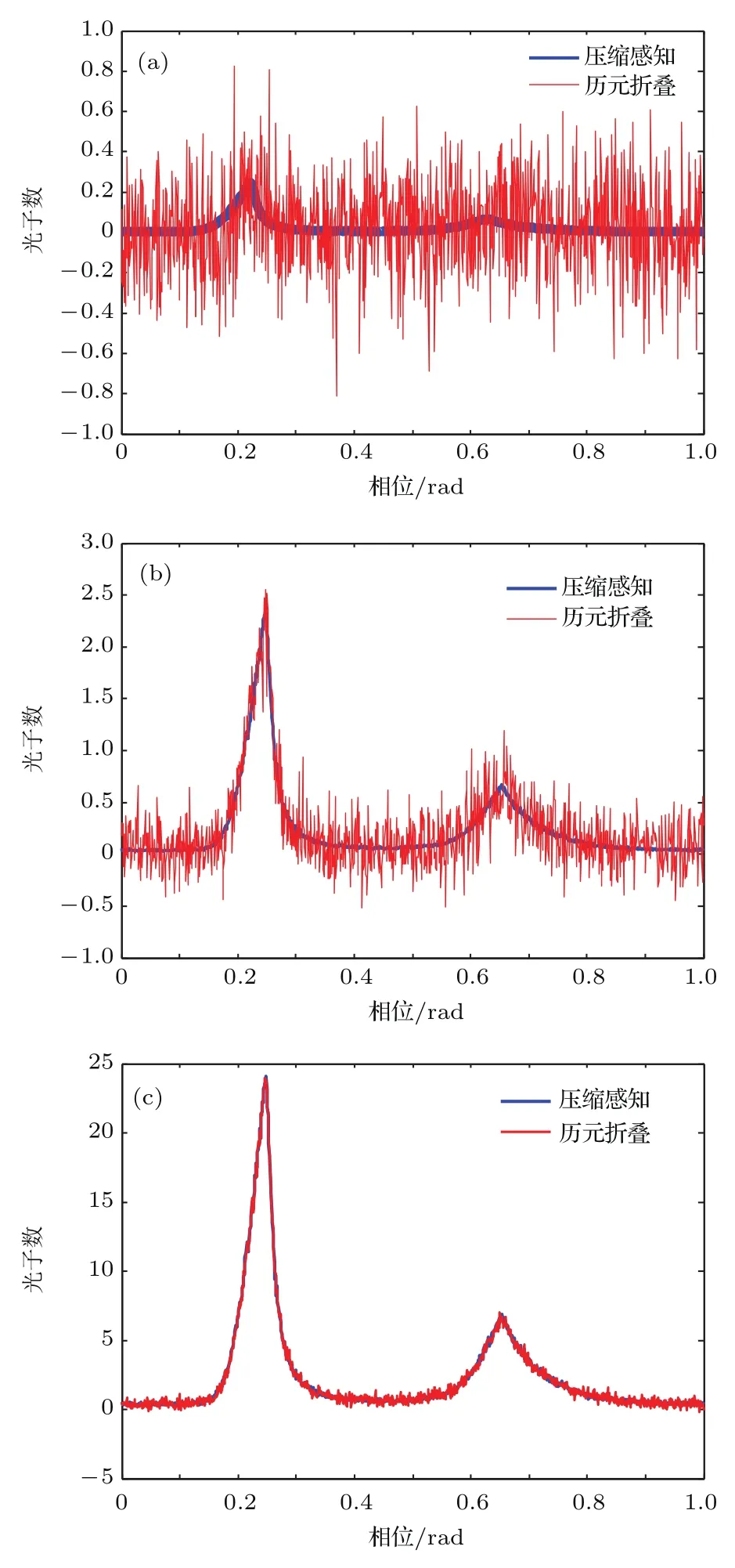
4.1.2 采样率的最优选择
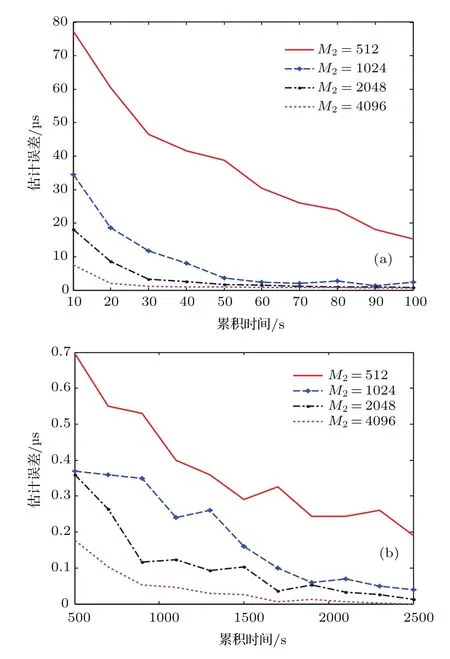
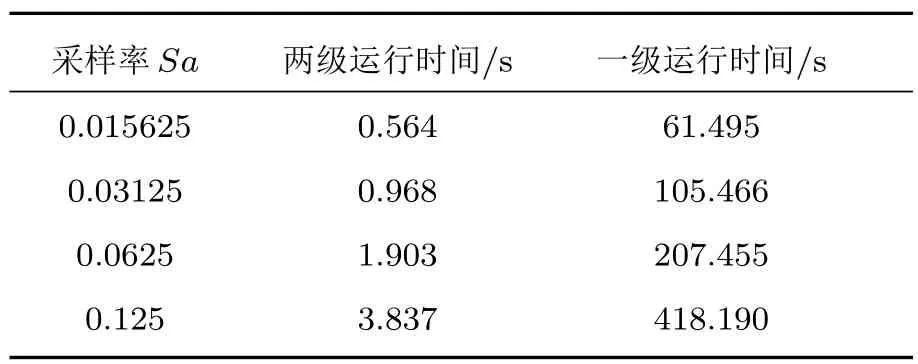
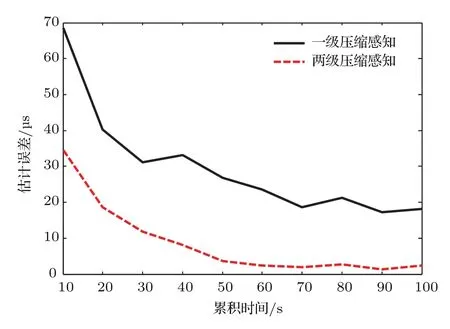
4.1.3 一级压缩感知与两级方法的估计精度
4.2 基于RXTE实测数据的仿真实验
5 结 论

