木网壳节点半刚性研究

周烨楠

(南京工业大学,南京 210000)

0 引 言

网壳结构具有受力简洁、造型优美、经济实用等优越性,近些年来被广泛应用于公共建筑、民用建筑和大中型工业建筑,尤其运用于屋面体系。规范中要求单层网壳应采用刚性节点,对于网壳结构的分析和设计都是建立在其节点为刚接的基础上。但是实际工程中有很多网壳节点既不属于刚接节点也不属于铰接节点,而是介于两者之间的一种半刚性节点。近年国内外网壳的理论及试验研究[1-3]表明,节点的刚度对网壳整体的稳定性和承载能力有着重要影响。

目前木结构网壳中,常用的节点有装配式植筋节点、钢板螺栓节点以及叠合节点等。本试验选取一种螺栓钢填板节点,这种节点将钢板隐藏在木杆件内,提高了节点连接的美观程度。

木材的不可焊性使得构件在工作时的受力状况复杂化。由于安装或加工精度,节点在承受外力时,连接节点处的相邻构件会发生相对转角或滑移,具有明显的半刚性特点。范峰[2]用3根单自由度的非线性转动弹簧Combin39模拟节点的转动刚度,半刚性节点的转动刚度就通过弹簧的实常数设置来控制。王凡[5]选用ANSYS中的Matrix27单元,通过单元刚度矩阵实数的变化来模拟节点刚度的变化。以上模型中,完全刚接与半刚性连接的区别在于,刚接的时候连接界面处没有相对转角,而半刚性连接,由于连接处的空隙等原因,两个连接界面处会有相对转动,但在木结构中,节点和构件连接的长度不可忽略。郭小农[6]将两节点之间的梁单元分成3个单元,将两端梁单元的截面惯性矩进行一定的折减,以此来考虑节点刚度时。徐菁[7]在梁单元有限元法的基础上,引入α系数对杆件惯性矩进行调节,以模拟球节点的刚性反映。但以上模型并未将节点的实际刚度与多段梁模型联系起来。

影响节点刚度大小的因素有很多,何敏娟[4]研究了不同螺栓排数对节点抗侧力性能的影响,结果表明增加螺栓排数可提高节点的强度和延性。故本文首先通过改变螺栓排数,得到试验节点弹性阶段的刚度。根据试验过程中节点的变形特征,确定合理的木网壳节点简化模型,通过将试验结果和模型理论值、分析值对比,验证简化模型的合理性。在此基础上,建立网壳半刚性有限元模型,探究木网壳节点刚度大小对木网壳极限承载力的影响。

图1 木网壳工程实例Fig.1 The case of wooden latticed shells

1 半刚性节点试验

1.1 节点尺寸

本文选择一种钢管-耳板螺栓节点作为网壳模型的节点,JD1单个耳板连接2个螺栓,JD2则连接4个螺栓,节点外形见图2。无缝钢管直径83 mm,壁厚5 mm,高度100 mm,其他尺寸见表1,节点抗弯试验分为2组,每组3个构件。钢管和耳板钢材选用Q235,连接节点与木杆件的螺栓采用直径为8 mm的8.8级高强度螺栓,考虑到安装问题,胶合木和耳板的预钻孔径取10 mm。

图2 试验节点形式(单位:mm)Fig.2 Joints form of test (Unit:mm)

表1 构件参数Table 1 The component parameter

1.2 试验装置及方案

网壳中常常将面荷载等效为网壳节点处的等效集中力,故本节点抗弯性能试验以位移控制,在节点中心处进行加载,测量节点位移值随荷载的变化,具体布置见图3。在构件上下布置位移计主要是为了抵消安装误差,防止个别位移计测量失效。

图3 位移计测点布置(单位:mm)Fig.3 Arrangement of displacement measuring points (Unit:mm)

为求连接部位界面与节点域之间的相对转角θ。由于木构件在加载平面内变形很小,视为刚体,由测点2和测点5的位移平均值推得连接部分界面a处的竖向位移,继而根据连接部分界面a与节点核心区的相对位移计算求得转角θ左,同理求得θ右,具体公式如下:

(1)

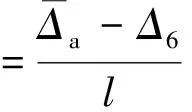
(2)

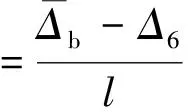
(3)

(4)

(5)

1.3 试验结果

1.3.1JD1组结果

木材端部与节点域之间保持有一定距离,以保证工作时主要由螺栓受力,以明确传力途径。以JD1-1为例,加载之初,随着位移增加,节点处竖向荷载增加较慢,螺栓与木杆件逐渐压实。当位移达到16.16 mm时,胶合木构件上部与节点域接触。当位移达到39.66 mm时,节点右侧杆件下部出现裂缝,随后节点左右杆件延栓杆处均出现裂缝。当位移达到58.66 mm时出现劈裂声,节点右侧杆件上部裂缝扩大,螺栓周围木材出现横向劈裂破坏,构件失效,加载结束。

图4 JD1-1裂缝开展及变形图Fig.4 Crack development and deformation of JD1-1

由弯矩转角曲线可知,节点前期的刚度相对较小,处于预紧阶段,随着位移增加其刚度逐渐增大,其荷载峰值为2.42 kN。

JD1组的3个构件的荷载-位移曲线及弯矩-转角对比图见图5和图6。

1.3.2JD2组试验结果

JD2组试验以JD2-1为例,加载之初同样经历杆件与螺栓压实的过程。当位移达到18.64 mm时胶合木构件上部与节点域接触。当位移达到44.26 mm时,节点左侧杆件上部和下部先后劈裂,随后裂缝逐渐增大,贯穿顺纹方向2个螺栓孔;位移达到58.66 mm时,下部螺栓孔位置沿顺纹方向剪切破坏,节点丧失承载能力,加载结束。构件JD2-1的极限承载力为3.41 kN。

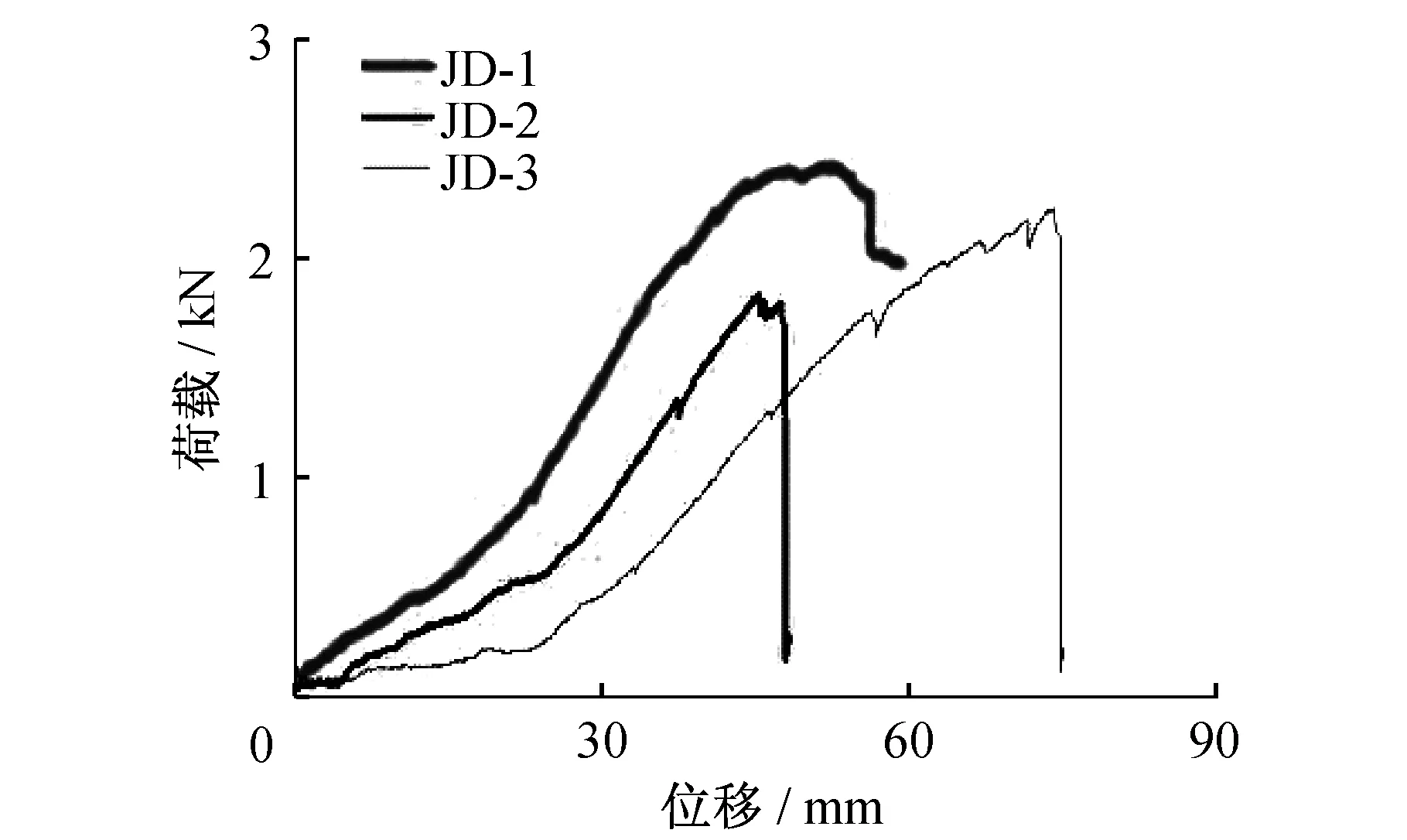
图5 JD1组构件荷载-位移曲线Fig.5 Load-displacement curves of JD1

图6 JD1组构件弯矩-转角曲线Fig.6 Moment-rotation curves of JD1

图7 JD2裂缝开展及变形图Fig.7 Crack development and deformation of JD2

节点2组的3个构件的荷载-位移曲线及弯矩-转角曲线对比图见图8和图9。

图8 JD2组构件荷载-位移曲线Fig.8 Load-displacement curves of JD2

1.3.3对比分析及结论

由试验现象可知JD1、JD2在集中力作用下的变形过程,初始阶段是一个预压的过程,螺栓与孔壁接触。进入弹性阶段,胶合木构件上部与节点域接触受压。当位移逐渐增大,杆件下部逐渐出现裂缝,最终节点受压区压溃,螺栓周围木材出现横向劈裂,节点脆性破坏。试验过程中,JD2相对JD1在连接部位变形的约束更加明显。

图9 JD2组构件弯矩-转角曲线Fig.9 Moment-rotation curves of JD2

为得到弯矩转角曲线,以单排螺栓节点JD1为例,弹性阶段内力图见图10,试验中测得的连接部分界面1与节点域的相对转角θ包括由弯矩引起的转角θ1和由剪力引起的转角θ2,根据实际试验的构件尺寸,由图11计算相对转角θ,公式如下:

θ=θ1+θ2

(6)

(7)

(8)

(9)

图10 JD1弯矩图Fig.10 Bending moment diagram of JD1

图11 JD1连接部位内力图Fig.11 Internal force diagram of the connection of JD1

带入数据得,

(750×100×100/2)=11.4

则θ与转角θ1之间的关系为θ=1.088θ1。根据式(6)-式(9)得弯矩转角曲线M-θ1,如图6所示。

同理,带入双排螺栓节点JD2数据得,

(1 000×160×160/2)=7.125

θ与转角θ2之间的关系为θ=1.14θ2。根据式(6)-式(9)得到弯矩转角曲线M-θ2,如图9所示。

由弯矩转角曲线看出,JD1、JD2两组构件在初始阶段转动刚度差异较大,这主要是由于安装时螺栓预紧,垫片与木材之间摩擦的差异造成的。接下来较长范围内具有较低的刚度,这主要是由于螺栓和预留孔壁之间存在间隙,在加载初期,螺杆和木材并未完全接触,因而节点表现为可变体系而产生局部刚体位移。

实际工程中,初始平缓段可通过安装完成后的预压消除,因而为了得到节点在网壳中工作时的真实刚度,取相同螺栓排数节点的弯矩转角曲线的平均值,并采用平移的方法[8],去除初始低刚度段之后的弯矩转角曲线为图12、图13,得JD1、JD2的平均弹性刚度分别为11.47 kN·m/rad、13.18 kN·m/rad,JD2相较JD1提高了14.9%,说明增加螺栓排数对节点的抗弯刚度有一定提高。

图12 JD1组构件平均弯矩-转角曲线Fig.12 Average moment-rotation curves of JD1

图13 JD2组构件平均弯矩-转角曲线Fig.13 Average moment-rotation curves of JD2

2 节点简化模型

考虑到若采用实体建模,建立考虑节点半刚性的网壳模型过程相当复杂,且计算量大,不利于应用于实际工程结构设计,故对节点模型进行简化,后采用梁单元建立半刚性模型。采用的简化模型能准确地反映节点变形特征,将试验得到的荷载位移曲线和半刚性模型联系起来。

2.1 试验节点简化模型

试验中看出,木结构网壳节点与钢网壳节点之间的区别在于,在钢板和木构件连接的部位不能简单看做杆件的一部分,其长度不可忽略,故不适合采用弹簧单元模拟,本文将试验节点简化为杆件+连接部分+节点域,抗弯刚度分别为E1I1、E2I2、E3I3,简化力学模型两端采用铰支,中心点处施加集中荷载,见图14。

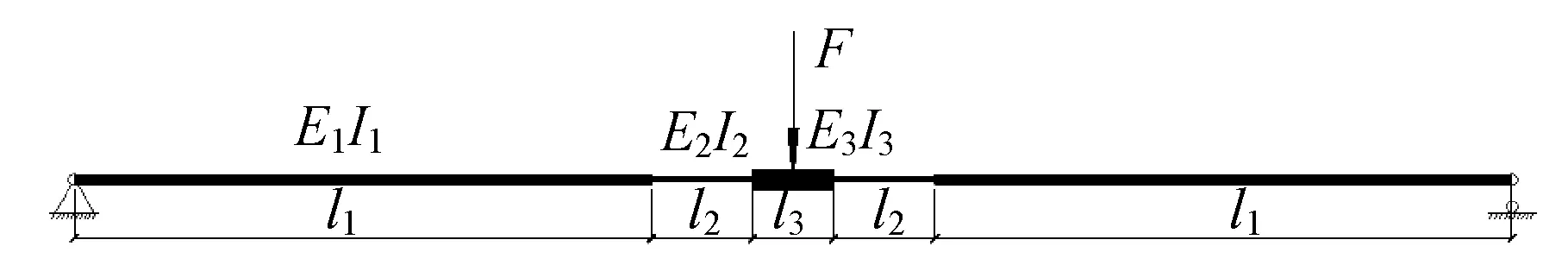
图14 节点简化模型Fig.14 Simplified model of joints

由荷载位移图5可知,JD1在1 500 N作用下节点刚度仍处于弹性段,模型各参数见表2,故根据力法计算单排螺栓节点在1 500 N作用下的跨中位移。

表2 模型参数Table 2 Parameters of the model

试验中节点域刚度E3I3远大于连接部分和木构件,可假设Δ3=0。根据力法[10]计算跨中位移过程如下:

(10)

代入JD1各参数得

Δ=2(Δ1+Δ2)=2×(0.506+12.595)=26.20 mm

同理,JD2在2 000 N作用下节点刚度仍处于弹性段,计算双排螺栓节点在2 000 N作用下的跨中位移,模型各参数见表2,跨中位移为27.54 mm。

2.2 试验结果和有限元分析对比

利用ANSYS中Beam189的非线性广义梁截面特征模拟节点域和杆件之间的连接部位,非线性广义梁单元是一种抽象的梁截面类型,可以直接定义弯矩与曲率的函数关系,该截面形式主要利用由试验获得的弯矩转角曲线对结构进行分析。与节点平面内抗弯刚度有直接联系的参数是Bsm2,连接部位弯矩与曲率的函数关系为

(11)

以JD1为例,其他参数设置见表3。

木网壳杆件采用Beam189 梁单元模拟,并均假设为各向异性的弹性材料,各参数取值见表3-表4。建模时,各部分的尺寸与之前计算时尺寸对应,由于节点域刚度较大,可视作刚体,其对最终节点变形的影响不大,故建模时忽略节点域。JD1建立的模型如图15所示。

表3 非线性广义梁截面特征参数设置Table 3 Parameter settings of the nonlinear general beam section

表4 花旗松正交各向异性参数Table 4 Orthogonal anisotropic parameters of Douglas fir

JD1分析得到的变形图为图16,节点杆件部分变形较小,主要为刚体位移,而连接部位变形较大,与试验得到的节点变形特征吻合。JD2由于是双排螺栓,连接部位的约束要大于JD1。试验值取平均荷载位移曲线对应值,分析结果与试验值和理论值对比如表5所示。

表5 节点中点位移值Table 5 Displacement of the midpoint of the joint

图15 JD1模型图Fig15 Finite element model of JD1

图16 JD1变形图Fig.16 Deformation of JD1

理论值和分析结果与试验值相当接近,JD1理论值与试验值相差1.8%,与分析值相差0.1%,JD2理论值与试验值相差10%,与分析值相差0.2%。结论,该简化模型能准确地反映节点变形特征,将试验得到的荷载位移曲线和半刚性模型联系起来。

3 半刚性节点网壳

木网壳实际建造过程中,由于节点制作和安装的误差,使节点并非完全铰接,也不可能完全刚接,此时就需要建立能够考虑节点半刚性的有限元模型。由于凯威特型网壳网格易于划分、受力合理等优点,故本文选择K6型网壳进行非线性稳定分析。

3.1 半刚性网壳模型

以K6型单层球面网壳为例,半刚性模型如图17所示。网壳跨度为9 m,矢跨比1/13,杆件截面选取与试验节点相同50 mm×100 mm,单排螺栓节点网壳杆件两端连接部分为100 mm,双排螺栓节点网壳杆件两端连接部分为160 mm,连接部分均采用Beam189的非线性广义梁截面特征模拟,杆件选用Beam189 梁单元,周边支承采用刚接。在用ANSYS对结构进行非线性屈曲分析时,利用弧长法进行屈曲失稳过程追踪,打开大变形开关,同时激活自动时间步长加速收敛。每次结果选取位移最大的那个节点的荷载-位移曲线作为代表。

图17 木网壳半刚性模型Fig.17 Semi -rigid model of wooden latticed shells

3.2 节点刚度对网壳极限承载力的影响

对于网壳结构设计来说,工程人员最关心的往往是网壳结构的极限承载力,以及对应的位移是否能够满足要求。从稳定方面讲,网壳荷载-位移曲线的第一个上极限点远高于其后的各个极限点,整条载荷-位移曲线呈现退化的趋势[ 9],所以一旦载荷超过第一个上极限点,那么网壳结构将失去稳定承载能力,从而变形越来越大直至彻底垮掉。因此选取荷载-位移曲线的第一个上极限点作为极限荷载。

选取位移最大的那个节点的荷载-位移全过程曲线,将本文中JD1、JD2作为节点的木网壳承载力与理想刚接、铰接网壳承载力对比,如图18可以看出,JD1、JD2木网壳的极限承载力明显大于节点按铰接考虑的数值,其曲线形态及趋势更接近于刚接网壳,且随着节点刚度的增加,结构达到极限荷载对应的位移逐渐减小。具体数值见表6。

图18 不同节点刚度网壳跨中位移全过程曲线Fig.18 Curves of shells with different bending stiffness

表6 不同节点刚度极限荷载和对应位移Table 6 Ultimate load and corresponding displacement with different bending stiffness

节点刚度越小,结构的容许变形越大,节点的变形趋势越容易确定其中抗弯刚度只有在杆件主要受压弯或节点有较大的相对位移时,影响变大节点具有一定的刚度时,结构不会发生跳跃性的屈曲。

4 结 论

(1) 由试验可知,螺栓排数的改变对构件承载力有明显的影响,JD2组构件的平均承载力比JD1组提高了91.7%,且延性更好。螺栓数量对节点的抗弯刚度有一定提高,JD2组构件的平均弹性刚度相较JD1组构件提高了14.9%。

(2) 将试验节点简化为杆件+连接部分+节点域的三段梁模型,根据力法计算得模型弹性段跨中位移理论值,JD1和JD2分别为26.20 mm、27.54 mm。

(3) 采用Beam189的非线性广义梁截面特征模拟节点域和杆件之间的连接部位,利用由试验获得的节点弹性段刚度对节点进行分析,节点杆件部分变形较小,主要为刚体位移,而连接部位变形较大,与试验得到的节点变形特征吻合,JD1和JD2跨中位移分析值分别为26.22 mm、27.60 mm。

(4) 理论值和分析结果与试验值相当接近,JD1理论值与试验值相差1.8%,与分析值相差0.1%,JD2理论值与试验值相差10%,与分析值相差0.2%。该简化模型能准确地反映节点变形特征,将试验得到的荷载位移曲线和半刚性模型联系起来。

(5) 以K6型单层球面网壳为例,将节点简化模型运用于半刚性木网壳模型,将本文中JD1、JD2作为节点的木网壳承载力与理想刚接、铰接网壳承载力对比,JD1、JD2木网壳的极限承载力明显大于节点按铰接考虑的数值,其曲线形态及趋势更接近于刚接网壳,且随着节点刚度的增加,结构达到极限荷载对应的位移逐渐减小。

参考文献

[1] 徐菁,杨松森.节点刚度对凯威特型单层球面网壳内力的影响[J].钢结构,2005,4(20):15-17.

Xu Jing,Yang Songsen.Influence exerted on the internal forces of Kiewitt single-layered spherical shells by the stiffness of joints[J].Steel Construction,2005,4(20):15-17.(in Chinese)

[2] 范峰,马会环,沈世钊.半刚性型螺栓球节点单层K8 型网壳弹塑性稳定分析[J].土木工程学报,2009,42(2):45-52.

Fan Feng,Ma Huihuan,Shen Shizhao.Elasto-plastic stability analysis of K8 single-layer reticulated shells with bolt-ball joint system[J].China Civil Engineering Journal,2009,42(2):45-52.(in Chinese)

[3] Aitziber Lopez,Inigo Puente,Miguel A.Serna.Numerical model and experimental tests on single-layer latticed domes with semi-rigid joints.Computer and structures,2007,85:360-374.

[4] 何敏娟,赵艺.螺栓排数和自攻螺钉对木梁柱节点抗侧力性能的影响[J].同济大学学报(自然科学),2015,43(6):845-852.

He Minjuan,Zhao Yi.Effect of bolt row and self-tapping screw reinforcement on lateral performance of bolted timber connection[J].Journal of Tongji University(natural science),2015,43(6):845-852.(in Chinese)

[5] 王凡,王星,张薇.节点刚度对单层网壳稳定性能的影响分析[J].钢结构,2015,30(8):43-45.

Wang Fan,Wang Xing,Zhang Wei.Analysis of the influence of joint stiffness on stability performance of single-layer reticulated shell[J].Steel Construction,2015,30(8):43-45.(in Chinese)

[6] 郭小农,沈祖炎.半刚性节点单层球面网壳整体稳定性分析[J].四川建筑科学研究,2004,30(3):10-12.

Guo Xiaonong,Shen Zuyan.Analysis of stability of single-layer spherical reticulated shells with semi-rigid joints[J].Sichuan Building Science,2004,30(3):10-12.(in Chinese)

[7] 徐菁,尚鹏,王秀丽.“变刚度”法在网壳结构设计中的应用[J].青岛建筑工程学院学报,2003,24(2):9-11.

Xu Jing,Shang Peng ,Wang Xiuli.The application of the rigidity-modulating method in the space shell design[J].Journal of Qingdao Institute of Architecture and Engineering,2003,24(2):9-11.(in Chinese)

[8] Xu Bohan ,Abdelhamid Bouchaïr.Appropriate wood constitutive law for simulation of nonlinear behavior of timber joints[J].Journal of Materials in Civil Engineering,2014,26(26):150-153.

[9] 符立勇.大跨度单层球面网壳的稳定性分析[D].成都:西南交通大学,2002.

Fu Liyong.The stability analysis of large-span single-layer spherical lattice shell[D].Chengdu:Southwest Jiaotong University,2002.(in Chinese)

[10] 龙驭球,包世华.结构力学教程(Ⅰ)[M].北京:高等教育出版社,2012.

Long Yuqiu,Bao Shihua.Structural mechanics tutorial (Ⅰ)[M].Beijing:Higher Education Press,2012.(in Chinese)