平行四边形易错题解析
周 杰
平行四边形是中心对称图形中最基本的几何图形,也是“空间与几何”领域的研究对象之一.下面,我们总结分析同学们在学习这部分知识时易出现的几类错误,希望能帮助大家走出误区.
一、基础不牢
例1 已知四边形ABCD,如图1,AD∥BC,试着再添加一个条件,使四边形ABCD为平行四边形.
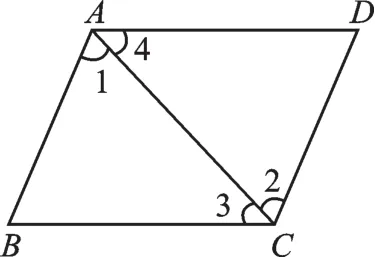
图1
【错解】∠3=∠4或AB=CD.
【剖析】由题意可知,四边形已经有一组对边平行,所以只要这组对边相等或另一组对边平行即可.而错解中由∠3=∠4推出的还是已知的AD∥BC,所以添加的这个条件是无效的.相反,添加∠1=∠2是可行的,因为由∠1=∠2可推出AB∥CD,此时利用两组对边分别平行的判定定理即可.错解中的AB=CD也不行,等腰梯形就是一个反例.
【正解】∠1=∠2或AB∥CD等.
【点评】这道题实际考查同学们对平行线判定的掌握情况,所以大家不仅要掌握好平行四边形的判定定理,还要对之前所学的平行线的判定方法了如指掌,这样,才能百战百胜.
二、理解不深
例2 已知四边形ABCD,有下列四个条件:①AB∥CD;②AD=BC;③∠A=∠C;④AB=CD,以其中的两个条件为一组,能判定四边形ABCD是平行四边形的有( ).
A.2组 B.3组 C.4组 D.5组
【错解】A.
【剖析】所给的四个条件中,两个一组,共有六种情况:①②、①③、①④、②③、②④、③④,其中①④、②④是课本上的判定定理,同学们能够很快判断出来,但是对于①③(一组对边平行,一组对角相等)这样的命题,一些同学没有进行深入思考,所以会有所遗漏.实际上,这也是一个真命题.
【正解】B.
【点评】对于平行四边形的判定问题,我们能够运用的工具不仅有教材中相关的判定定理,还有一些相关的真命题(推论),把它们的条件稍作转化,就可以进行判定了.所以,在解题过程中,同学们要认真审题,对照判定定理仔细思考,方能得出正确结论.
三、考虑不周
例3 平面直角坐标系内有A(-2,1)、B(-3,-1)、C(0,-1)三点,点D也在坐标平面内,且以A、B、C、D四个点为顶点的四边形是一个平行四边形,则点D的坐标为 .
【错解】(1,1).
【剖析】如图2,先把A、B、C三点的坐标在平面直角坐标系中标出来.

图2
因为以A、B、C、D四个点为顶点的四边形是一个平行四边形,所以线段AB不是边就是对角线.过C、A、B三点分别作AB、BC、AC的平行线,然后利用平行四边形的定义,将符合条件的点找出,即D1、D2、D3.因此符合题意的D点共有3个.
【正解】(1,1)、(-5,1)、(-1,-3).
【点评】已知三个点求第四个点,使它们构成平行四边形,关键是根据平行四边形的定义(两组对边平行的四边形是平行四边形),正确画出所有符合条件的平行四边形.顺便提醒同学们,以后遇到没有给出图形的平行四边形问题时,要善于画出所有可能的情形,当题目中有不确定的已知条件时,要注意分类讨论,全面考虑,这样才不至于漏解.
四、说理不严
例4 已知平行四边形ABCD,如图3所示,AC、BD交于点O,OE⊥AD于E,OF⊥BC于F.求证:OF=OE.

图3
【错解】∵四边形ABCD是平行四边形,∴OA=OC,∵OE⊥AD,OF⊥BC,垂足分别为E、F,∴∠AEO=∠CFO=90°,又∠AOE=∠COF(对顶角相等),∴△AOE≌△COF(AAS),∴OF=OE.
【剖析】错解中,因为题目中未明确指出点E、O、F在同一直线上,因此不能肯定∠AOE与∠COF是对顶角.若用到这个条件,必须先给出严格的证明.
【正解】∵四边形ABCD是平行四边形,∴OA=OC,AD∥BC,∴∠DAO=∠FCO,∵OE⊥AD,OF⊥BC,垂足分别为 E、F,∴∠AEO=∠CFO=90°,∴ΔAOE≌ΔCOF(AAS),∴OF=OE.
【点评】运用平行四边形的性质证明三角形全等,当对应角的位置关系似乎是对顶角时,要根据所给出的条件认真识别,看它是否满足对顶角的条件.若不满足,则需另找判断三角形全等的条件,不可主观臆断.

