金融机构存款预测的组合预测模型研究

冯 宇，王 聪

（1.国家开发银行股份有限公司 吉林省分行，长春130022；2.西安电子科技大学 机电工程学院，西安710071）

引言

金融机构本外币存款余额主要由企事业单位存款和城乡居民储蓄存款组成，它是地方乃至全国经济统计中非常重要的指标。对金融机构本外币存款余额做出科学合理的预测，可为相关决策部门研究居民的收入水平、资金流向、调整储蓄利率、居民的消费习惯等影响存储行为的因素提供依据，从而可更好地促进吉林省经济的快速发展。

关于预测的方法种类繁多，从经典的单耗法[1]、统计分析法[2]，到目前的灰色预测法[3-6]、简单移动平均法[6，7]、ARMA[4，8，9]，甚至刚刚兴起的神经网络法[10-12]、优选组合法[13]和小波分析法[14]，这些预测方法各有结构特点、优缺点和适用范围，因此，在对某一个问题进行预测时，可使用不同的常见预测方法进行尝试，选择最佳的预测方法。

由于组合预测方法尤其适用于信息不完备的复杂经济系统[15]，因此本文选用灰色模型 GM（1，1）[3-6]、三次指数平滑模型[16]和BP神经网络模型[10-12]三种预测模型，应用Shapley值权重分配法[17，18]确定各预测模型的权重，从而构建组合预测模型[19-21]并对吉林省金融机构本外币存款余额进行组合预测。

一、单一模型的建立

（一）灰色模型GM（1，1）

灰色系统理论[3-6]是基于关联空间、光滑离散函数等概念定义灰导数与灰微分方程，进而用离散数据列建立微分方程形式的动态模型，记为GM（Grey Model），即灰色模型是利用离散随机数经过生成变为随机性被显著削弱且较有规律的生成数，建立起微分方程形式的模型，这样便于对其变化过程进行研究和描述。

设x（0）为n个元素的数列x（0）=（x（0）（1），x（0）（2），…，x（0）（n）），x（0）的 AGO[3]生成数列为 x（1）=（x（1）（1），x（1）（2），…，x（1）（n）），其中，则定义x（1）的灰导数为：

令 z（1）为数列 x（1）的紧均值数列，即：

定义GM（1，1）的灰微分方程模型：

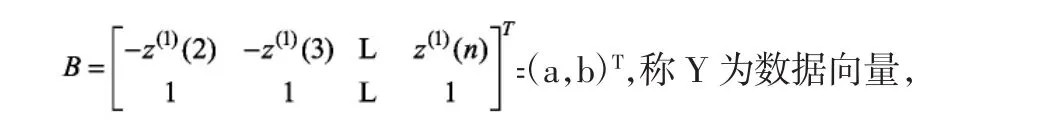
B为数据矩阵，u参数向量，则GM（1，1）模型可表示为矩阵方程Y=Bu。有最小二乘法可求得：

（二）三次指数平滑模型

指数平滑法[16]是对预测对象的全部历史序列数据，通过加权平均从而进行预测的一种方法。三次指数平滑预测法的计算公式为

式中，yt+T——金融机构本外币存款余额，T、t——预测的时间周期数和预测起始年，at、bt、ct——三次指数平滑的平滑系数，计算公式见式（6—8）。

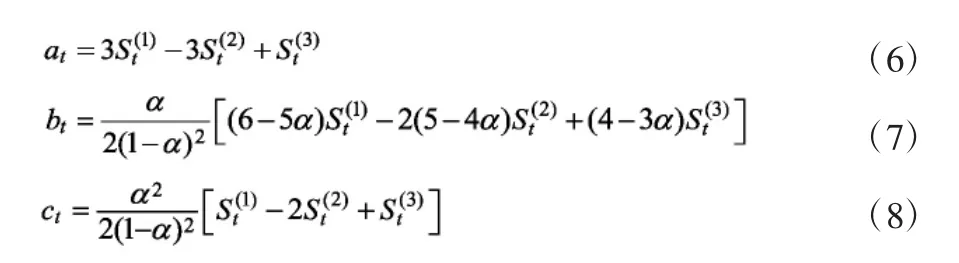
其中，0≤α≤1。经过多次试验后，选取α=0.3。指数平滑值计算公式为

式（9）中：yt——t起始年t的对应原始数据。

（三）BP神经网络模型

BP神经网络[10-12]包括信号的前向传播和误差的反向传播两个方面，即计算实际输出时按从输入到输出的方向进行，而权值和阈值的修正从输出到输入的方向进行。BP神经网络模型如图1所示，BP神经网络算法设计流程如图2所示。

图1 BP神经网络模型

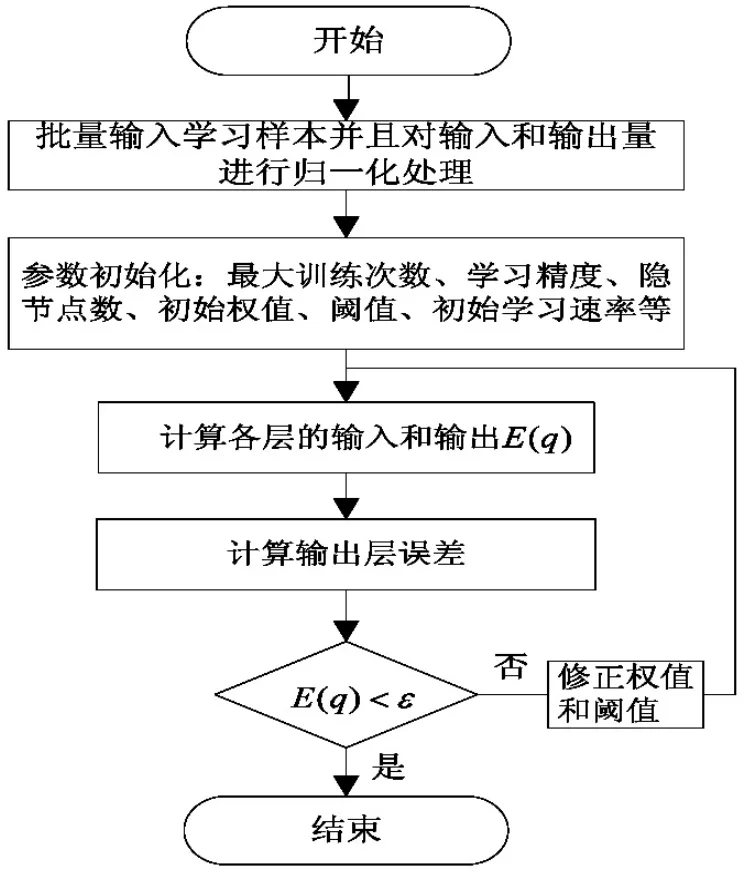
图2 原理流程

图 1 中，xj为输入层第 j个节点的输入，j=1，…，M；wij为隐含层第i个节点到输入层第j个节点之间的权值；θi为隐含层第i个节点的阈值；准（x）为隐含层的激励函数；wki为输出层第k个节点到隐含层第i个节点之间的权值，i=1，L，q；ak为输出层第 k 个节点的阈值 k=1，L，L；ψ（x）为输出层的激励函数；ok为输出层第k个节点的输出。

（四）单一模型优缺点总结

灰色模型GM（1，1）经过多次输入数据检验，模型代码本身是良好的，但由于金融机构存款数据离散程度太大导致了模型结果的误差较大，因此灰色模型GM（1，1）预测在输入数据有一定增减趋势时，预测效果才能较好；采用三次指数平滑模型处理数据时，可发现预测整体趋势很准确，但个别数据的预测准确度不高，因此在预测数据发展趋势时较适合采用此方法；BP神经网络预测通过模拟生物神经元系统，经过多次训练最终得到较合适的结果，但训练次数较多，不易操作，且存在较高的偶然性。在其他方面选用预测方法时可依据不同情况进行不同选择，从而建立合理的数学模型。其实在一般情况下最合理的就是组合预测模型。组合预测模型集中了多个单一模型的优点，有效减小了单一模型预测的较大误差，适合大量不规则数据的预测处理，因此在随机预测领域会有很大的用处。

二、组合预测模型

组合预测模型[19-21]汇聚了单个模型中的蕴含的有用信息，从而更易适应未来变化，减少了预测的风险性，提高了预测精度。组合预测方法利用数学语言描述如下：假设有m种预测模型对同一预测对象进行预测，则由这m种单一预测模型构成的组合预测模型为

式（12）中，y赞t为 t时刻组合预测模型的预测值；y赞it为 t时刻第 i个预测模型的预测值（i=1，2，…，m）；ki为第 i个预测模型的权系数

本文采用Shapley值法确定组合预测模型中的权系数。Shapley值法[17，18]是L.S.Shapley于1953年提出的用于解决多人合作对策问题的一种数学方法，Shapley值实现的是每个合作成员对该合作的平均贡献。基于Shapley值的共同收益分摊方法最大的优点就是在于其分摊原理和分摊结果易于被各个合作方视为公平，分摊结果易于被各个合作方所接受。

设有n种预测模型来进行组合预测，记为I={1，2，…，n}，对于I的任何子集s，t（表示n种模型中的任一组合），E（s），E（t）表示各自组合的误差。定义如下：

（1）对于 I的任一子集 s，t，都有 E（s）+E（t）≥E（s∪t），E（s），E（t）为各自预测时产生的误差；

（2）s哿I，yi表示第i种模型在合作最终分摊的误差值，总有 yi≤E（i）；

（3）对于n种预测模型参与的组合预测产生的总误差E（n），将在n种预测模型之间进行完全分配，即

设第i种预测模型误差的绝对值的平均值为Ei，组合预测的总误差值为E，则有

式（13）中，m为样本的个数；|eij|为第i种模型第j个样本的误差绝对值。

Shapley值法的权重分配公式为

其中，ω（|s|）——第i种模型应承担的组合边际贡献，ω（|s|）=；（si）——组合中去除模型i；i——参与组合的某个预测模型；Ei——i预测模型分得的误差量，即Shapley值；s——I中的任何子集；|s|——组合中的预测模型的个数。

由式（13）、（14）可得出组合预测中各预测方法的权重计算公式

式（16）中，n——预测模型个数。

三、实证研究

（一）数据来源

吉林省2006—2015年金融机构本外币存款余额如表1所示，其变化趋势如图3所示。

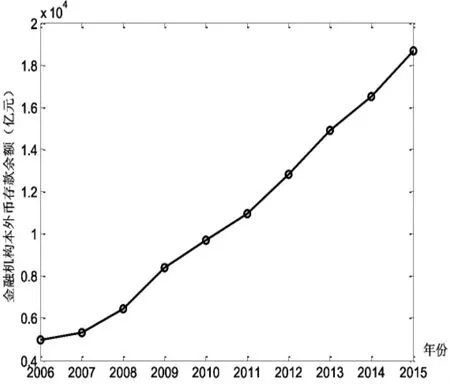
图3 2006—2015年金融机构本外币存款余额

由表1和图3可以看出，金融机构本外币存款余额总体呈上升趋势。2006年末，吉林省金融机构本外币存款余额总量为4 964亿元，至2015年末，已达到18 684亿元，2006—2015年这十年间年均增长1 372亿元。

（二）灰色模型 GM（1，1）的实证结果

依据式（1—4），结合表1中吉林省2006—2015年金融机构本外币存款余额数据，可建立灰色预测模型GM（1，1）。通过建立的模型预测2006—2015年的存款余额，从而验证灰色模型GM（1，1）的预测精度。具体预测值和预测精度如表2所示。

由表2可得，灰色模型GM（1，1）预测的平均相对误差值为0.045 7，即4.57%。由此可知，灰色模型GM（1，1）具有很好的拟合精度，可用于吉林省金融机构本外币存款余额的预测。

（三）三次指数平滑模型的实证结果

本文取初始平滑值根据表1中2006—2015年吉林省金融机构本外币存款余额的历史数据，利用式（5～11）进行计算，其预测结果如表3所示。

由表3可得，三次指数平滑模型预测的平均相对误差值为8.93%。由此可知，三次指数平滑模型的拟合精度不如灰色模型GM（1，1），但总体上依然可用于吉林省金融机构本外币存款余额的预测。

令t=2015，则吉林省金融机构本外币存款余额的三次指数平滑预测公式为

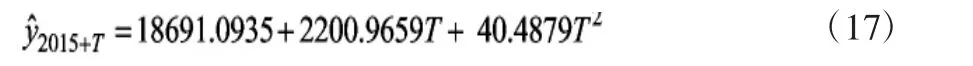
根据式（17），可对2015年以后的存款余额进行预测。

（四）BP神经网络模型的实证结果

依据表1中2006—2015年吉林省金融机构本外币存款余额的历史数据，利用matlab工具箱计算，BP神经网络模型的预测结果如表4所示。

由表4可得，BP神经网络模型预测的平均相对误差值为3.06%。由此可知，BP神经网络模型具有较好的拟合精度，优于前两种预测模型，可用于吉林省金融机构本外币存款余额的预测，但是由于需要多次迭代过程，所以计算效率并不高。

（五）组合预测模型的实证结果

按表2、表3、表4的计算结果，可求得组合预测的总误差为

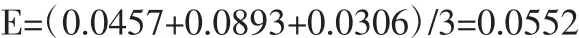
依据Shapley值的概念，参与组合预测模型总误差分配的模型为：I{1，2，3}，它所有子集的组合误差分别为：E{1}、E{2}、E{3}、E{1，2}、E{1，3}、E{2，3}、E{1，2，3}，其数值的大小为该子集所包括的向量的误差平均值，计算结果如表5所示。

表1 吉林省2006—2015年金融机构本外币存款余额

按照Shapley值计算公式可以计算出组合中对应模型的Shapley值为

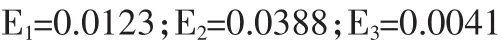
三个模型分担结果之和为：E1+E2+E3=0.0552。根据上面的计算结果来计算组合加权系数，根据权重公式（17），可计算出各个预测方法的权重为：

表2 2006—2015年灰色模型GM（1，1）的预测值和预测精度值

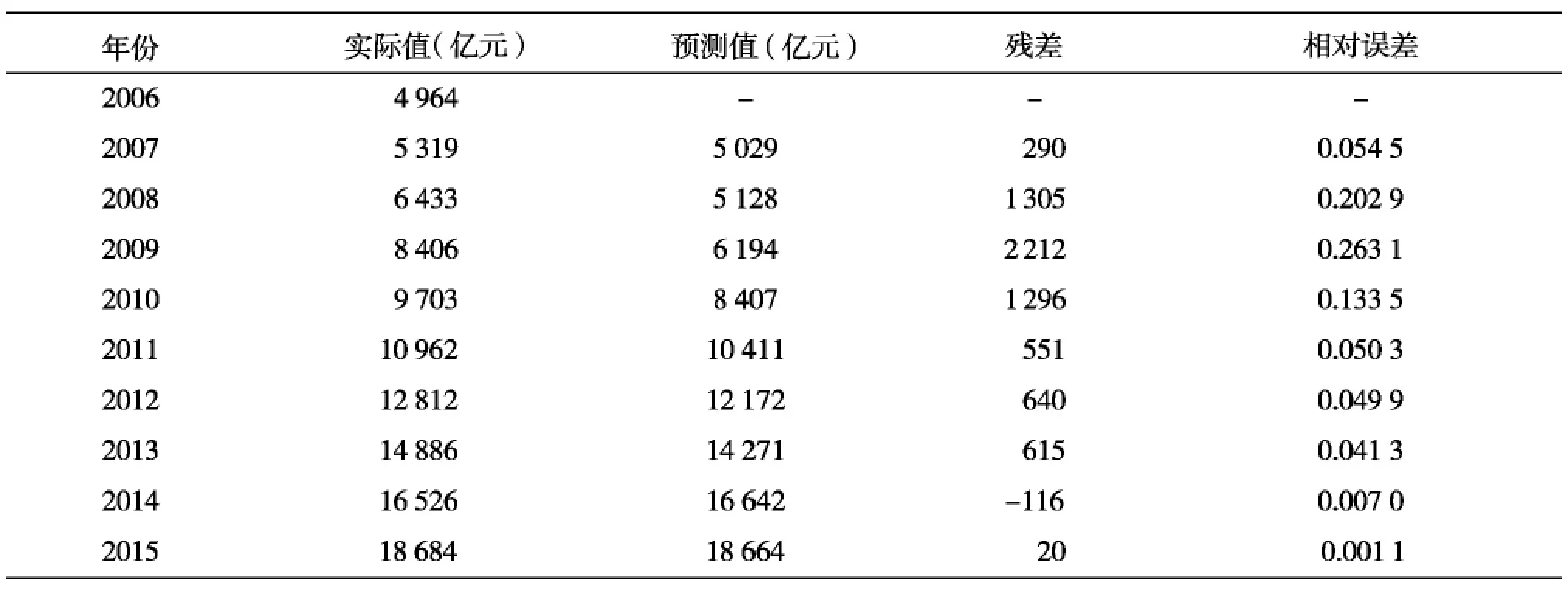
表3 2006—2015年三次指数平滑模型的预测值和预测精度值

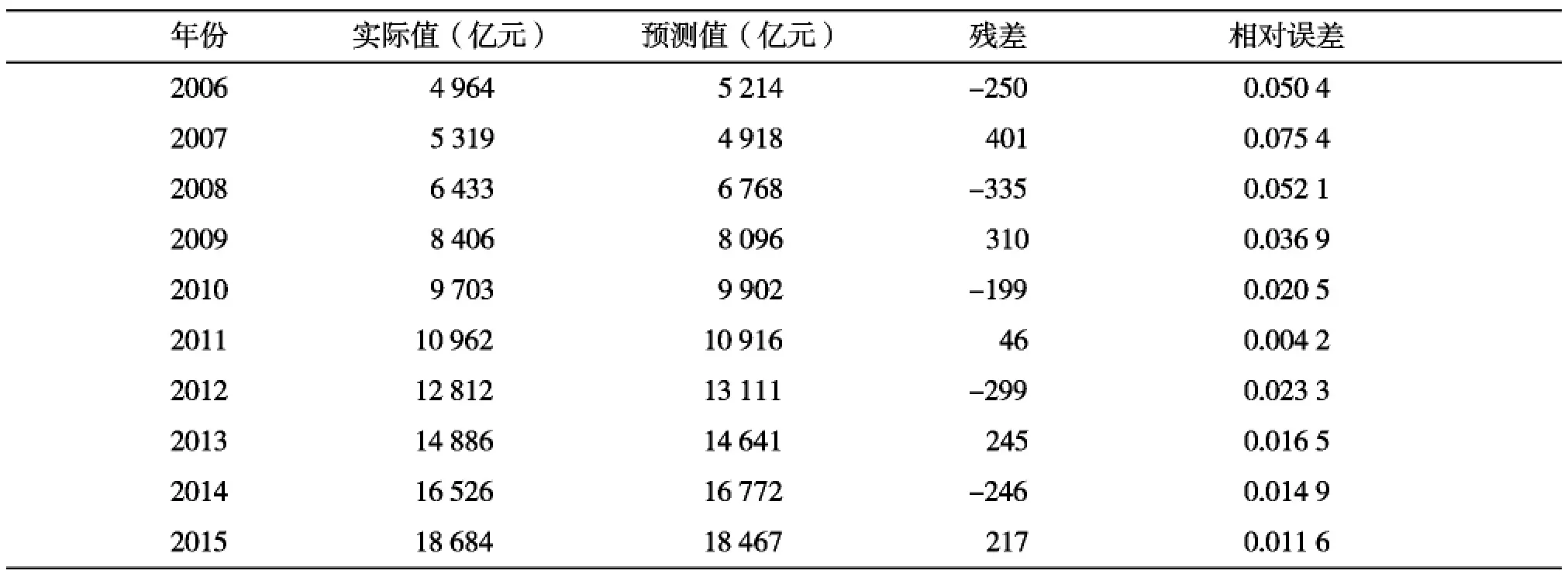
表4 2006—2015年BP神经网络模型的预测值和预测精度值

表5 预测误差分摊计算结果

根据所得的权重及公式（13），可得组合预测模型为：

式（18）中——组合预测值——灰色模型预测值；——三次指数平滑模型预测值——BP神经网络预测值。

利用此组合预测模型对2007-2015年吉林省金融机构本外币存款余额进行预测，其组合预测模型的预测值与误差如表6所示。

由表6中数据可知，组合预测模型平均绝对相对误差为1.74%，模型的预测精度很高，并且预测精度高于选定的单一预测模型的预测精度。

表6 2006—2015年组合预测模型的预测值和预测精度值

利用该组合预测模型对吉林省2016—2020年金融机构本外币存款余额进行预测，其结果如表7所示。

表7 2016—2020年吉林省金融机构本外币存款余额预测值

从表7中可以看出，2016年吉林省金融机构本外币存款余额为20 933亿元，到2020年达30 708亿元。2016—2020年存款余额年均增长率为10.45%。

结语

采用灰色模型 GM（1，1）、三次指数平滑三种预测模型和BP神经网络模型，对吉林省金融机构本外币存款余额进行预测，又利用Shapley值权重分配法来合理确定单一预测方法的权重，从而建立出组合预测模型进行预测，结果表明，构建的组合预测模型预测精度高于选定的任一预测模型。因此，本文的研究为吉林省金融机构本外币存款余额预测提供了一种实用的新方法和范式。

参考文献：

[1]王丽婕，廖晓钟，高阳，等.风电场发电功率的建模和预测研究综述[J].电力系统保护与控制，2009，37（13）：118-121.

[2]王健，严干贵，宋薇，等.风电功率预测技术综述[J].东北电力大学学报，2011，31（3）：20-24.

[3]张大海，江世芳，史开泉.灰色预测公式的理论缺陷及改进[J].系统工程理论与实践，2002，22（8）：140-142.

[4]王聪，杨建斌，邓颖.数学建模方法在风电功率预测中的应用[J].太阳能学报，2015，36（5）：1081-1087.

[5]刘思峰，杨英杰.灰色系统研究进展（2004—2014）[J].南京航空航天大学学报，2015，47（1）：1-18.

[6]王天真，汤天浩，张圣杰，等.基于灰色预测的粒子滤波算法[J].高技术通讯，2012，22（4）：423-428.

[7]左山，鲁晶晶，田磊，等.简单移动平均预测法在航材保障中的应用[J].科技信息：学术版，2008，（30）：87-88.

[8]丁明，张立军，吴义纯.基于时间序列分析的风电场风速预测模型[J].电力自动化设备，2005，25（8）：32-34.

[9]Zhang Jianyong，Wang Cong.Application of ARMA model in ultra-short term prediction of wind power[C].2013 International Conference on Computer Sciences and Applications（CSA）.Wuhan，China，2013：361-364.

[10]彭怀午，刘方锐，杨晓峰，等.基于人工神经网络的风电场短期功率预测[J].太阳能学报，2011，32（8）：1245-1250.

[11]周扬，吴文祥，胡莹，等.基于组合模型的能源需求预测[J].中国人口·资源与环境，2010，20（4）：63-68.

[12]王守相，张娜.基于灰色神经网络组合模型的光伏短期出力预测[J].电力系统自动化，2012，36（19）：37-41.

[13]王翠茹，杜鹃.优化组合预测的设计与分析[J].东北电力技术，2006，27（6）：5-7，23.

[14]李炎，高山.风电功率短期预测技术综述[C]//中国高等学校电力系统及其自动化专业第二十四届学术年会论文集.北京，2008：2540-2544.

[15]王金山，杨国超.一种基于时序可变加权系数的组合预测模型[J].重庆理工大学学报，2012，26（2）：118-121.

[16]杨文光，严哲，于健，等.基于混沌三次指数平滑模型的CPI预测研究[J].陕西科技大学学报：自然科学版，2015，（6）：179-182.

[17]李书金，郦晓宁.模糊联盟的Shapley值与稳定性[J].系统工程理论与实践，2011，31（8）：1524-1531.

[18]李维乾，解建仓，李建勋，等.基于改进Shapley值解的流域生态补偿额分摊方法[J].系统工程理论与实践，2013，33（1）：255-261.

[19]曾庆聪，王金婷.组合模型在深圳港货物吞吐量预测中的应用[J].大连海事大学学报，2007，33（z1）：136-138.

[20]宁艳艳，郑春华，方小艳，等.基于组合模型的能源需求预测[J].企业导报，2016，（8）：191，82.

[21]芦森.基于组合模型的中国能源需求预测[D].成都：成都理工大学，2010.