基于有限元法的高拱坝分区变形模量反演分析

李宗樾 程 井 张枝阳 庞井龙

(1.贵州省大坝安全监测中心， 贵阳 550002； 2. 河海大学 水利水电学院， 南京 210098)

我国高拱坝建设成就斐然：二滩、龙羊峡、李家峡等稳定安全运行，拉西瓦、锦屏一级、溪洛渡、小湾、大岗山相继蓄水．高拱坝的成功建设标志着我国坝工建设的水平，其稳定、安全运行至关重要[1]．为了实现对大坝真实运行状态的监测评价，高拱坝坝体坝基及库区布设了大量的变形、渗流等相关监测仪器及设备．大坝综合评价及预测通常基于位移反馈模型展开，而位移反馈模型的核心是坝体坝基物理力学模型的概化及其相关变形模量参数的确定[2]．现阶段高混凝土坝坝体及坝基变形模量参数反演一般采取有限元分析方法，其主要思路有两种：1)基于水位及温度等实测资料建立位移的统计模型[3-4]；根据水压荷载条件下的有限元位移值与位移统计模型的水压分量之差建立目标函数[5]，然后利用常规优化方法如正交试验法等，反演出变形模量参数；2)先依据实测资料进行温度场反馈分析[6]，然后再结合该温度结果及其他荷载进行施工及运行全过程位移分析；根据该位移结果与实测整体位移之差建立目标函数，进而反演出变形模量参数．

对于混凝土重力坝，总体来说两种方法均可取得较好的结果．而对于拱坝，两种方法均有一定难度，具体体现在：1)高拱坝属高次超静定结构，受地形地质条件及坝体结构影响，其位移响应模型非常复杂[7]，统计回归模型中的关于水压的多项式有时不能满足要求；因此，基于该统计回归模型的水压分量用来反演大坝及坝基变形模量，可能存在较大的误差；2)拱坝温度场时空分布复杂多变，施工及运行全过程温度场及位移场仿真工作量巨大，且参数反演过程中需要多次正分析．

本文推导了分区有限元计算近似模型，并在此基础上提出了一种新的高拱坝坝体坝基变形模量参数反演分析方法：首先利用不同变形模量组合下的有限元模型计算结果作为位移基序列，来取代回归模型中的水压相关因子；对不同变形模量组合系数及其对应基序列的回归系数进行加权即可得到坝体坝基分区变形模量．该方法既能反映坝体坝基位移的复杂响应，又无须多次重复坝体全过程仿真计算分析，可以较为快速准确地反演出拱坝坝体及地基的变形模量参数．

1 基于有限元法的拱坝反馈模型

1.1 拱坝水平径向位移统计模型

混凝土拱坝水平径向位移主要受水荷载、温度、时效三大因素的影响．为简化计算，只选取水压分量、温度分量和时效分量作为变化因子，建立如下监测回归模型[7]：

(1)

其中，δ0为回归分析常数项；ai、bi分别为水位、气温及坝体温度因子回归系数；H为监测日水头，H=库水位-坝基高程；ΔδTi为气温、典型测点温度或典型断面典型浇筑层平均温度的变化值；p为温度因子个数；c为时效因子回归系数；θ为监测日至监测基准日的累计天数除以100．

1.2 基于有限元法的力学计算模型

给定荷载作用下的大坝坝体坝基整体有限元模型，其不同材料分区的综合变形模量记为(Ei，i=1，…，n)．该模型的力学问题可表述为：

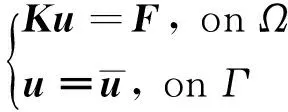
(2)

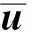
i≠jandi，j=1，…，n

(3)

上式平衡方程中的刚度矩阵Ki为对称奇异矩阵，无法直接求解位移．采用直接代入法引入位移边界条件：

(4)

(5)

于是整体问题可表示为：

KFud=F*

(6)

或

(7)

(8)

式中，F*随界面位移而变化，当Γ及分区界面均为零位移约束时，F*为常量；否则需要通过若干次迭代来确定．一般情况下，考虑如下假定：

1)大坝处于小变形状态；各分区变形模量相对设计值的变化倍数的优选范围可依据工程经验及实际物探成果来选定，初选可取[0.5～2]；

2)对于任一分区，其与其他分区交界面上的位移分解为均匀的平动位移uc1及剩余部分uc2，假定平动位移部分uc1占主体．

此时，依据刚度矩阵对平动位移的相容性，在变形模量变化不大的情况下，位移向量ud可以看成n个位移基向量udj的线性组合，其中udj对应于变形模量组合系数为Mj={1/E1j1/E2j…1/Enj}T．

1.3 于有限元的快速近似反演方法

依据1.2节理论基础，提出一种新的高拱坝变形模量参数的快速反演分析方法：

1)依据设计及施工情况建立考虑材料分区的坝体坝基系统的整体有限元分析模型；

2)对蓄水及运行阶段的温度、水位及变形资料进行回归统计模型概化，建立规则化时间序列；

3)依据坝体坝基分区个数n，建立n组互无关的分区变形模量基本组合Mj={1/E1j1/E2j… 1/Enj}T；利用水位序列，得到有限元模型在水荷载作用下的位移响应基序列{Yj}；

4)利用该位移基序列{Yj}代替统计回归模型式(1)中的所有水压相关序列{Hj}，即：

(9)

然后进行统计回归得到各变量因子的回归系数；

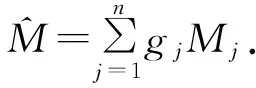
为了保证其合理性和完备性，构造坝体坝基分区变形模量组合系数时应特别注意：1) 依据材料变异性大小、空间位置以及监测位移对各部分材料参数的敏感性进行分区；2) 各分区变形模量值与设计值之比应建议限制在合理范围内，建议取值[0.5，2.0]；3) 对于单个分区内包含多种材料的情况，可假定其变化倍数相同，或者采用加权平均法得到其近似等效弹模．

2 工程实例

2.1 工程概况及有限元分析模型

鱼简河枢纽工程位于乌江一级支流息烽河上，于2005年建成．主体大坝为碾压混凝土双曲拱坝，坝高81 m，坝顶高程1 062 m，坝面弧长179.73 m．大坝在拱坝中心线左侧的0+098.405断面布置一条正垂线和一条倒垂线观测坝体挠度，在高程1 012 m衔接．正垂线悬挂装置位于坝顶1 062 m高程，分别在1 037 m、1 012 m高程设观测点；倒垂线固定端高程1 051 m，垂线孔深入基岩30 m．

采用1 062 m高程测点在2005年8月23日至2008年6月8日期间的实测径向位移进行变形模量参数反演．坝基有限元模型按左右两岸侧方向取约2倍坝高，建基面以下基岩厚度取100 m，顺河向上游侧延伸约1.5倍坝高，下游侧延伸约2倍坝高．坝体坝基整体有限元模型含材料分区及坝体网格如图1～2所示，采用六面体单元，共计50 780个单元，56 934个结点．计算时基岩侧面均施加法向约束，底面施加全约束，外荷载仅考虑水荷载，材料本构模型采用线弹性模型．设计阶段坝体混凝土弹模、右岸坝肩、左岸坝肩及底部坝基近似变形模量取值分别为EⅠ0=39 GPa、EⅡ0=6.32 GPa、EⅢ0=7.81 GPa、EⅣ0=6.0 GPa．

图1 拱坝三维整体有限元模型

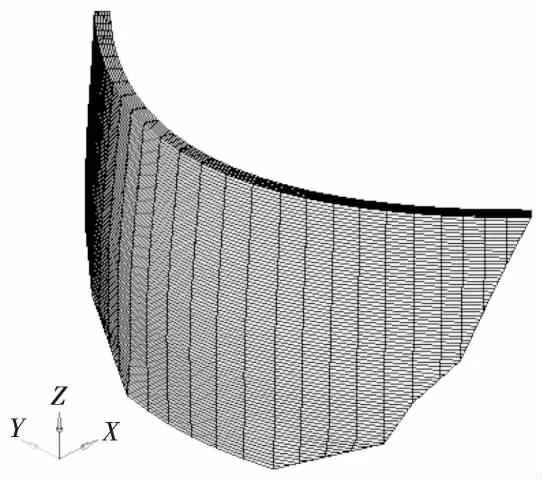
图2 坝体网格

2.2 常规方法1计算结果

基于常规方法统计回归模型公式(1)，得到坝顶径向整体位移的统计回归模型[8]，其中整体实测值、整体拟合值及各位移分量如图3所示．可以看出，回归模型拟合良好，水压分量随水位变化而变化，两者相关性明显，但水压分量偏大．以该统计模型水压分量作为目标序列，采用正交试验法来反演坝体坝基变形模量[5]，最终优选结果为EⅠ=30 GPa、EⅡ=5.73 GPa、EⅢ=7.46 GPa、EⅣ=5 GPa．以此参数进行有限元仿真计算得到的位移与统计模型水压分量值对比图如图4所示，可见有限元仿真值较统计模型水压分量明显偏小，反演结果不理想，分析原因可能是拱坝结构太复杂，统计模型出现过拟合．

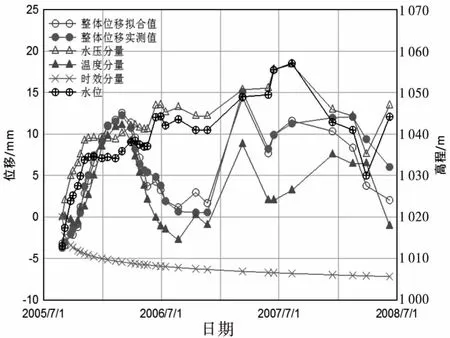
图3 常规方法1整体实测位移、拟合位移及各分量

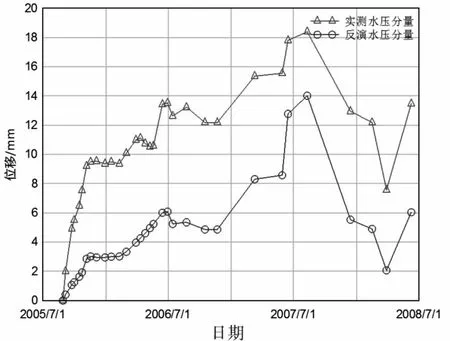
图4 常规方法1实测水压分量及反演水压分量

2.3 本文快速反演方法计算结果

基于1.3节快速反演方法，拟定4种分区变形模量组合工况见表1，将各工况有限元计算得到的位移响应基序列Y1，Y2，Y3，Y4，作为位移监测模型的回归因子，得到的回归模型的位移基序列回归系数分别为0.182、0.082、0.033和0.783．回归模型径向位移整体实测值、整体拟合值及各位移分量如图5所示．结果显示，径向位移实测值与拟合值吻合良好；与2.2节常规统计模型相比，水压分量相对较小；径向位移水压分量与库水位变化相关关系明显；2007年5月以前坝前水位较低时，水压分量随水位而变化的速率相对较慢，坝体变形受温度影响较大；时效分量为顺河向位移，初期变化较大，后期趋于稳定．总体而言，该统计模型较常规统计模型更为合理．

依据回归系数得到分区变形模量的反演值分别为：EⅠ=39.24 GPa、EⅡ=6.11 GPa、EⅢ=8.46 GPa、EⅣ=5.64 GPa，据此进行有限元反馈分析，得到有限元反演水压分量与回归模型水压分量值如图6所示，二者吻合度很高，证明了新反演方法的正确性与合理性．图7给出了正常水位条件下基于变形模量反演值的水平位移响应．

表1 拱坝材料分区变形模量组合表

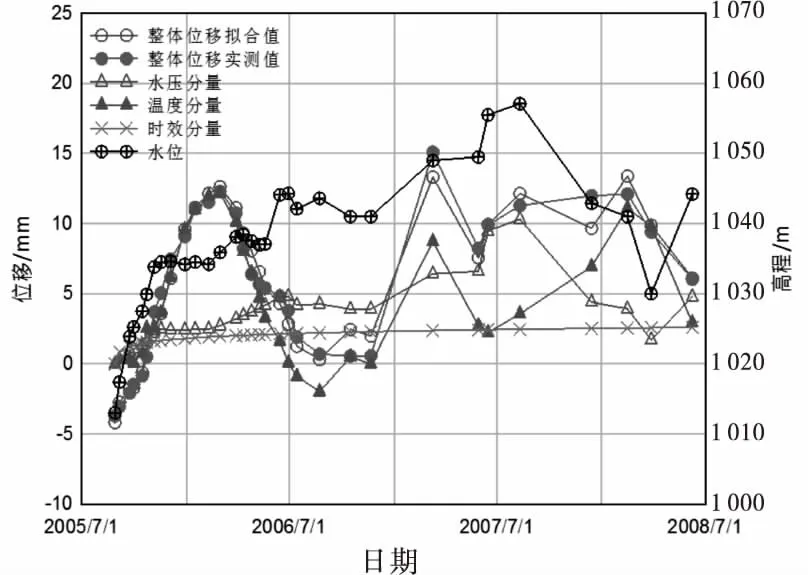
图5 新方法整体实测位移、拟合位移及各分量

图6 新方法实测水压分量及反演水压分量

图7 正常蓄水位下基于变形模量反演值的位移响应

3 结论及展望

以鱼简河拱坝为例，提出了一种高拱坝分区变形模量快速反演方法，主要结论如下：1)推导了分区有限元计算近似力学模型；依据刚度矩阵对平动位移的相容性，在变形模量变化不大且坝体处于小变形的情况下，位移向量可以近似分解成n个位移基向量的线性组合．2)给出了快速反演方法的基本原理及步骤，主要包括坝体坝基分区、设定初始变形模量组合、通过有限元分析得到对应于各种组合的位移基序列、基于位移基序列的大坝位移回归模型及最终变形模量计算．3)通过鱼简河工程验证了方法的合理性及高效性．新方法得到的回归模型更加合理，且水压分量与水位相关良好；坝体混凝土、右岸坝肩、左岸坝肩及底部坝基4个分区的变形模量反演结果分别为EⅠ=39.24 GPa、EⅡ=6.11 GPa、EⅢ=8.46 GPa、EⅣ=5.64 GPa，与设计值较为接近．

本文提出的变形模量参数反演方法无需大量正算，计算效率较高，具有良好的应用价值，但仍存在如下问题：1)利用位移基序列进行位移模型回归时，要求回归系数在一定合理范围内，这属于约束优化问题，需要研究合适的优化算法；2)本文算例针对某具体时段进行反演，假定了变形模量为常量．如何将其进一步推广至时变弹模相关参数的反演，还需继续深入研究．3)该反演算法概念明确，充分利用了有限元计算成果和监测回归模型成果．下一步如能与结构力学方法如拱梁分载法等相结合，则有望进一步提高算法的精度．

参考文献：

[1] 朱伯芳，张超然，张国新．高拱坝结构安全关键技术研究[M]．北京：水利水电出版社，2010．

[2] 郑东健，李凤珍，赵 斌．基于变形资料的拱坝坝肩稳定安全度分析[J]．河海大学学报(自然科学版)，2008，36(5)：590-594．

[3] 李广春，戴吾蛟，杨国祥，等．时空自回归模型在大坝变形分析中的应用[J]．武汉大学学报(信息科学版)，2015，40(7)：877-881．

[4] 王 伟，沈振中，钟启明．基于混合蛙跳算法的混凝土坝加权变形预报模型[J]．水利水电科技进展，2013，33(2)：37-41．

[5] 赵英华，李同春，程 井，等．基于统计模型及有限元法的重力坝变形模量反演[J]．水电能源科学，2015，33(12)：96-100．

[6] 程 井，李同春，陈祖荣，等．基于有限元法的高混凝土坝温度场反馈分析模型探讨[J]．三峡大学学报(自然科学版)，2014，36(2)：11-16．

[7] 顾冲时，吴中如．大坝与坝基安全监控理论和方法及其应用[M]．南京：河海大学出版社，2006．

[8] 庞先明，陈 浩，晏卫国．鱼简河碾压混凝土拱坝原型观测资料分析[J]．水利规划与设计，2008，21(4)：66-70．