特高压线路对对空雷达站电磁干扰的防护间距

唐 波 杨嘉炜 黄 力 郝 斌

(三峡大学 电气与新能源学院， 湖北 宜昌 443002)

随着国际安全局势的复杂多变，各地出现了大量对周边电磁环境要求苛刻的雷达台站[1-2]．以特高压输电线路为骨架的电网建设和对空雷达站间不可避免地出现了越来越突出的电磁干扰问题[3-5]．而目前国家所使用的防护规范仍是根据20多年前的标准GB13618-92《对空情报雷达站电磁环境防护要求》，其涉及的最高电压等级为500 kV，显然对于目前的状况存在一定局限性．为此，需要针对两者的防护间距问题做出进一步研究．

当前已有公开文献对特高压输电线路与周边电磁设施防护间距的研究，但其主要针对对象是处于中短波频段(0.3～30 MHz)内的无线电台站[6，7]．而对空雷达站工作频段处于80～3 000 MHz，影响可能更为严重．与一般无线电台站的防护准则相比，对空雷达站有其特殊的防护要点，最主要一点体现为：雷达站除了对周边环境及设施有相应的防护规定外，还需保证探测距离损失在5%以内．

为此，基于对空雷达站电磁防护准则和雷达回波方程，提出了特高压输电线路与对空雷达站的理论求解模型，并应用数值分析法研究两级系统之间的防护间距问题．以允许探测距离损失为基准，通过对特高压铁塔的塔型、一定线路长度下的铁塔基数、雷达入射波角度的建模和仿真分析，得出了雷达探测损耗随两者间距距离变化时的规律，最后对现有防护间距标准提出了建议．

1 防护间距与探测距离损失

雷达进行目标探测时，探测距离是衡量其探测性能强弱的一项重要指标[8]．根据目前研究，雷达探测距离的评估方式主要是通过实地探测或者缩比实验完成的[9]，但这两种以试验为基础的数据采集无疑会耗费大量资源，实施过程十分困难．因此，如何有效评估探测距离损失就是解决防护间距问题的先行条件．

假设雷达发收天线共用，雷达信号的接收方程和雷达探测距离公式分别如下：

(1)

(2)

式中，R是雷达距离目标距离，Rmax是雷达最大可探测距离，Pt是雷达发射功率，Pr是雷达回波功率，G是发收天线增益，λ是雷达波长，Pmin是雷达可检测到的最小回波信号，σ是雷达散射截面(RCS， Radar cross section)．

根据标准规定，在保证发射功率不变的情况下，通过对式(1)等号两边的简单变换，5%的允许最大探测距离损失可以等效为允许探测功率损耗降低0.9 dB，而雷达探测功率损耗可通过分贝换算公式得出：

ΔP=10lg(Pr/Pt)

(3)

式中，ΔP是雷达探测功率损耗．

因此，对雷达探测距离损失的求解即可转化为对探测功率损耗的分析．结合式(1)和式(2)可以看出，影响雷达探测功率损耗的主要变量因子是雷达散射截面σ，其它如发射功率Pt、波长λ、天线增益G等参量则取决于雷达的自身属性．

根据雷达散射截面(RCS)的定义可以得到其表达式为：

(4)

式中，Es为目标散射场强，Ei为雷达入射波场强．

结合方程(1)～(4)，通过对σ的求解即可得到探测功率损耗大小，进而对防护间距进行判定．

2 对空雷达站防护间距的求解

2.1 防护间距的规程算法

当前防护间距的确定是根据等效噪声带宽和最大允许效干扰场强直接进行计算的．计算公式如下：

(5)

Ejqmax=Ujfmax+20lgf-G-10lgZ+VEgp+L-9.8

(6)

Ujfmax=0.48Unf

(7)

式中，Dmin是所需防护间距，E0是不同电压等级常量，f是雷达工作频率，Bn是噪声带宽，Ejqmax是最大允许干扰场强峰值，Ujfmax是最大允许干扰电压有效值，Z是雷达接收机输入阻抗，ΔEgp是准峰值场强与峰值场强分贝数之差，L是雷达天线系统损耗，Unf是等效本机系统噪声电压有效值．

标准中对E0、ΔEgp、Unf的参数取值有明确规定，可根据其研究对象进行相应赋值．然而，噪声带宽Bn是由线路本身参数决定，其与线路谐振频率相关；天线系统损耗L大小是由内部系统损耗以和外部人为操作及环境损耗两方面因素共同决定的，而现场实际情况的复杂多变，诸如操作损耗、环境影响损耗等因素大小很难确定．并且，由于实际线路杆塔和线路模型结构复杂，很难通过公式直接进行计算，应考虑数值算法．

2.2 采用数值算法求解防护间距

由2.1节分析可知，采用数值算法求解防护间距时，需要求解出目标铁塔的散射场强Es的大小，进而才能确定探测距离损失和防护间距的关系，因此首先需要建立散射场求解模型．

如图1所示为建立特高压输电线路与对空雷达站防护间距的求解模型示意图．从图1中可以看出，输电线路沿y轴方向建立，雷达站位于中间的1基铁塔横线路方向并沿x轴方向进行信号发收．雷达与最近的1基铁塔的防护间距为D，当线路与雷达站的防护间距需要调整时，可将线路看作一条直线并沿x轴方向平移，以此来模拟不同情况下的干扰损耗从而确定最佳防护间距．

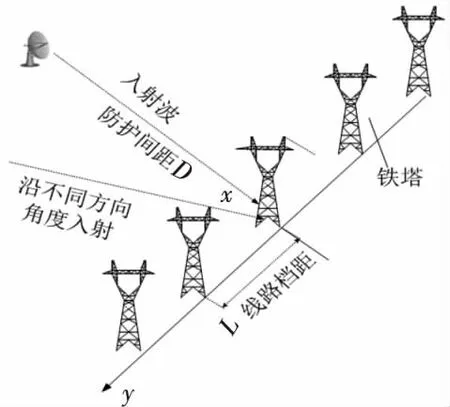
图1 散射场求解模型

模型建立完成后，就需要选择合适的算法进行求解．在高频散射问题求解中，空间任意点散射场Es可采用LE-PO法求解．LE-PO法是一种基于Stratton-chu积分方程的高频快速求解方法，文献[10]详细分析了散射场的求解步骤，在此不做过多叙述．模型和算法确定后，通过改变雷达站与输电线路的相对位置以及各个变量因子，将求得的散射场结果带入前文公式进行计算，以0.9 dB为标准阈值进行结果筛选，从而确定最佳防护距离．

3 防护间距的具体求解

3.1 模型及参数设置

建立特高压输电铁塔模型时，选用酒杯塔、猫头塔和干型塔进行分析，为了避免塔高因素带来的影响，因此在建模时统一两种塔型的高度为65 m．如图2所示为3种塔型的模型．

图2 特高压输电塔模型

根据特高压工程标准设计规范，铁塔角钢规格选用L200型，宽度为0.2 m；雷达天线激励源采用垂直极化平面波模拟．

以500 kV电压等级的输电线路防护间距规定为基础，在研究特高压线路防护间距时，设置1 000 m为起始防护距离进行研究．雷达与铁塔距离从1 000 m依次线性增加至2 500 m，步长为100 m．

3.2 防护间距的具体求解

根据对空雷达站工作所处频段，选取100 MHz、500 MHz、1 GHz、3 GHz分别对特高压输电线路铁塔的塔型、档距以及当雷达入射波角度为30°、60°和90°时探测损耗与防护距离的变化规律进行分析．

3.2.1 塔型对雷达探测损耗的影响

如图3所示为酒杯塔、猫头塔和干型塔3种塔型对雷达探测损耗随防护间距的变化规律．图中虚线表示标准规定的0.9 dB探测损耗要求．

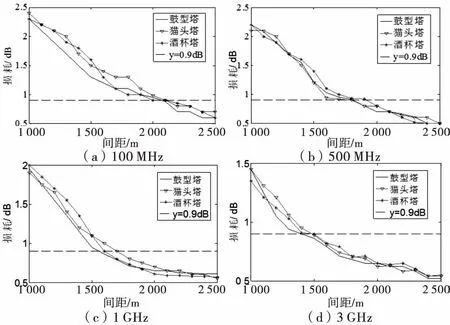
图3 防护间距与损耗变化规律(塔型)

从图3中可以看出，随着防护距离的提升，3种塔型对雷达探测造成的损耗都呈现减小趋势，并且通过图a和图d对比得出，当频率从100 MHz升高到3 GHz时，铁塔对雷达探测造成的损耗是降低的，相应的防护距离也随之减小．如当频率为100 MHz时，3种塔型造成的损耗都约为2.3 dB，需要的防护距离为2 100 m；而当频率提升至3 GHz，损耗降低至约1.4 dB，防护距离为1 500 m时就能满足0.9 dB的探测损耗要求．同时，结合图(a)～(d)4个图发现，在4种不同频率下激励下的3种塔型损耗变化规律基本一致，因此认为塔型不是影响雷达探测损耗的主要因子．

3.2.2 铁塔数量对雷达探测损耗的影响

设置总线路长度为2 000 m，分别研究放置3基、5基、7基不同数量的铁塔对雷达探测损耗的变化规律．根据图3得出结论，塔型不是主要的影响因子，因此在研究铁塔数量时统一采用酒杯塔进行建模分析．

如图4所示表示不同频率下当铁塔基数变化对探测损耗带来的影响．通过图4(a)～(d)4个图对比发现，和设置5基或7基铁塔相比，设置3基铁塔在4种频率激励下对雷达探测损耗的影响都是最小的，相应的其防护间距要求也最低．如在图4(d)中，当频率为3 GHz时，3基铁塔的防护间距为1 250 m时即可达到标准限值．然而，随着铁塔基数的增加，从3基到5基再到7基，以图4(c)为例，探测损耗呈现一个先增加后降低的趋势，损耗最大值出现在设置5基铁塔的时候．和3基塔、5基塔相比，7基塔造成的探测损耗介于两者之间，图4中其余3个图变化规律也基本相同．

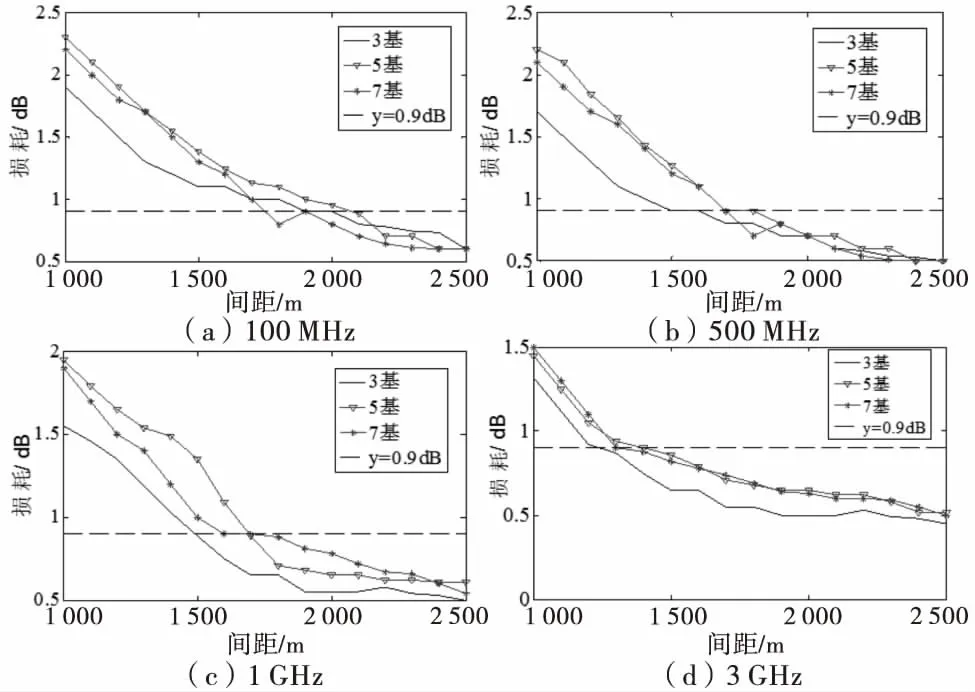
图4 防护间距与损耗变化规律(铁塔数量)

3.2.3 雷达入射波角度对探测损耗的影响

选取当雷达入射波为30°、60°和90°3种情况下进行研究分析，如图5所示．

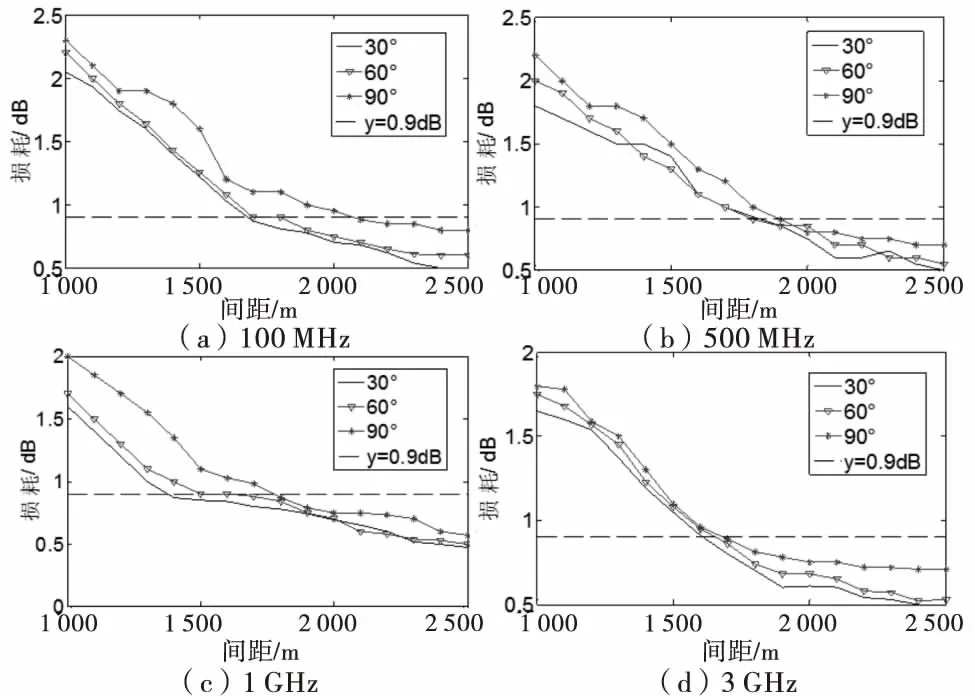
图5 防护间距与损耗变化规律(入射角度)

从图5中可以看出，当雷达入射角度与输电线路垂直即为90°时，造成的探测损耗影响最大，最大值出现在频率为100 MHz时，损耗为2.3 dB，根据求解结果，此时防护间距要求约为2 200 m；在图5中，由(a)～(d)4个图对比发现，当入射角度为30°和60°时，损耗的变化规律十分接近.因此认为当雷达入射波垂直线路走向时造成的探测损耗更为明显．

4 结 论

1)根据本文研究结果，塔型对雷达探测损耗的影响较小，主要的影响因子是铁塔数量以及雷达入射角与线路走向的夹角．在考虑3种变量因子的最大影响情况下，建议防护间距设置1900m～2100m；同时，在实际特高压工程建设中，输电线路走向应尽量避开雷达入射的垂直方向，并且在一定的线路总长内，尽量减小铁塔建设基数．

2)本文研究对实际的特高压工程建设在一定程度上具有指导意义，对今后的特高压工程线路规划具有实际参考价值．

参考文献：

[1] Senem Makal Yucedag， Okan Mert Yucedag， Huseyin Avni Serim. Analytical Method for Monostatic Radar Cross Section Calculation of A Perfectly Conducting Wind Turbine Model Located Over Dielectric Lossy Half Space[J]． IET Radar, Sonar and Navigation, 2014, 8(8)： 965-970．

[2] Tran Vu La, Francois Le Pennec, Christophe Vaucher. Small Wind Turbine Generic Model Design for Bts Radio Interaction Studies[C]//24th International Symposium on Personal, Indoor and Mobile Radio Communications： Fundamentals and PHY Track, IEEE, London, UK, 2013： 866-870．

[3] 刘振亚，张启平，董 存，等．通过特高压直流实现大型能源基地风、光、火电力大规模高效安全外送研究[J]．中国电机工程学报，2014，34(16)：2513-2522．

[4] 刘振亚．特高压电网[M]．北京：中国经济出版社，2005．

[5] 邬 雄，万保权．输变电工程的电磁环境[M]．北京：中国电力出版社，2009：83-94．

[6] Zhang Xiaowu, Tang Jian, Zhang Huanguo, et al．Reradiation Interference Computation Model of High Voltage Transmission Line to the Shortwave Radio Direction Finding Station[C]//20th International Zurich Symposium on Electromagnetic Compatibility, Zurich, Switzerland： IEEE Electromagnetic Compatibility, 2009：309-312．

[7] 唐 波，文远芳，张小武，等．中短波段输电线路无源干扰防护间距求解的关键问题[J]．中国电机工程学报，2011，31(19)：129-137．

[8] 丁鹭飞，耿富录，陈建春．雷达原理[M]．北京：电子工业出版社，2014．

[9] 陈京平，刘建平，田军生．特高压输电线路线塔对电磁波的衰减效应试验研究[J]．现代电子技术，2008(15)：146-148．

[10] 唐 波，黄汉生，孙子昂，等．基于LE-PO法的特高频输电线路无源干扰求解[J]．信阳师范学院学报(自然科学版),2017,30(2)：287-292．