时滞基因调控网络的稳定性与分叉分析

吴 燕 王宝贤

(三峡大学 理学院，湖北 宜昌 443002)

基因调控网络是一个强大的动力系统．它描述了基因(mRNA)和蛋白质(Protein)之间的联系．近些年，随着科学技术研究的不断进步，基因调控网络在生物医学、工程科学、化学及数学领域异军突起[1-4]．

众所周知，生物体对外部信号的响应是通过由基因网络的高连通性和复杂性实现的基因预编码响应所实现的．细胞内脱氧核糖核酸形成染色体，包含了生物体随外界环境生长所需要的各种信息，与有机体中的复杂机制、生理调节等功能密切相关，因此它在生物医学方面扮演着重要的角色[4]．从生物角度来看，稳定性和时滞是基因调控网络的两个重要性质．文献[5]研究了基于时滞独立的基因调控网络的稳定性，文献[6]研究了随着时滞变化环状基因调控网络的稳定性与分叉分析．文献[7]研究了混合时滞下的基因调控网络的稳定性与分叉分析．文献[3]研究了混合控制下时滞的微积分基因调控网络的分叉分析等．基于严密的理论分析和数学数值实验，它已经取得了很大的进展．再如，基因开关[8]、抑制网络[9]、单时滞[6，10]等．这些实验的结果表明，数学模型对于研究活生物体的结构、洞察基因调控网络的本质，进而提取基因信息等无疑是一个强大的工具．

1 基因调控网络模型

对于混合的调节机制，采用一种基因-蛋白质组结构建立数学模型，因此给出混合调控机制如下[11]：

(1)

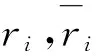
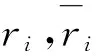
因此，当θ=0时系统(1)可简化为以下形式：

(2)

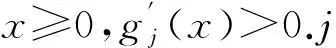
引理1[13]若f是分谐波函数，则

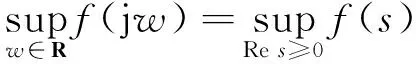
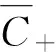
引理2[14]设A，B，C，D都是n×n矩阵，且|A|≠0，AC=CA，则有

2 特征方程的建立和稳定性分析

每一个基因调控网络都是自生的动力系统，对应函数并非总是平衡状态．在基因调控网络中平衡点的存在条件对其模型的动态行为有很重要的影响．在进行更深的稳定性分析之前，首先讨论特征方程及其平衡点的求解．为了简化，设G为以下矩阵：

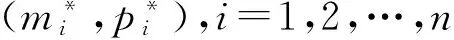
(3)

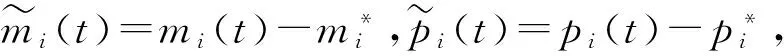
(4)

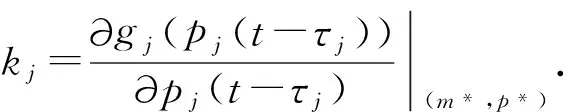
其中s∈C代表特征值，C是所有复数的集合．进一步化简得

(5)

于是系统(4)的特征方程为：

其中A=diag(a1，a2，…，an)，C=diag(c1，c2，…，cn)，D=diag(-d1e-sτ1，-d2e-sτ2，…，-dne-sτn)都是对角矩阵，T=(Tij)n×n=(-Gijkje-sτj)n×n，In是n×n的单位矩阵．由引理2得

Δ(s)=det((sIn+A)(sIn+C)-DT)=

对上述矩阵进行如下分块：

其中A1=(s+a1)(s+c1)，B1=(-die-sδ1T12-d1e-sδ1T13，…，-d1e-sδ1T1n)，C1=(-d2e-sδ2T21，-d3e-sδ3T31，…，-dne-sδnTn1)T，D1=diag((s+a2)·(s+c2)，…，(s+an)(s+cn)).因此，特征方程为

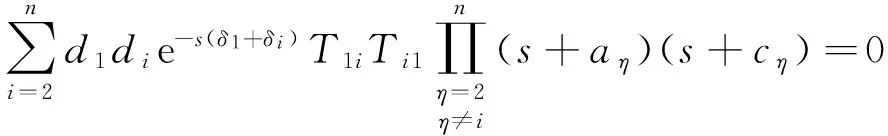
(6)

通过观察，得到等式：e-s(δ1+δi)T1iTi1=G1iGi1·e-s(τ1+τi+δ1+δi)k1ki，方程(6)左右两边同时乘以多项式：es(τ1+δ1)es(τ2+δ2)…es(τn+δn)，得

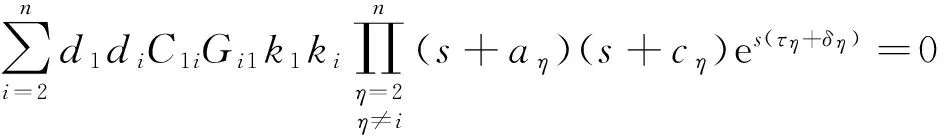
(7)

令αi=d1diG1iGi1k1ki，得

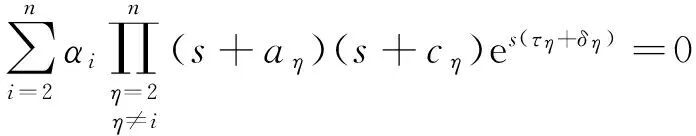
(8)

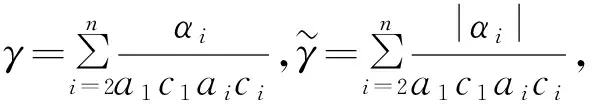
定义1称基因调控网络(2)局部时滞无关稳定的，若对任意的离散时滞τi，δi≥0，i=1，2，…，n，特征方程(6)的所有特征根都有负实部．

定理1若γ>1，则对任意的离散时滞τi，δi≥0，i=1，2，…，n，基因调控网络(2)不稳定；若γ=1，网络(2)出现鞍结点分叉．

证明：令s=0，

因此当γ=1时，Δ1(0)=0，即s=0是特征方程(8)的根．当γ>1，则有

因Δ1(s)为s的连续函数，由介值定理可知，Δ1(s)至少有一个正实根s0，使得Δ1(s0)=0成立．定理得证．

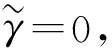
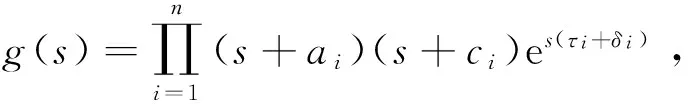
(9)

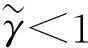
|Δ1(s)|=|g(s)-M(s)|≥|g(s)|-|M(s)|>0

(10)

式(10)意味着任意复数的非负实部对应特征方程没有根．等价地，对于任何离散时滞，特征方程(8)的所有特征根都有负实部，根据定义1，基因调控网络(2)局部时滞无关稳定，故得证．

上面已讨论了有时滞的基因网络的分叉分析．通过观察可以发现，不带时滞时对应的结果与有时滞时相同，这里不再重述．

3 数值仿真

基因调控网络的动态表现取决于其结构大小、生化参数和平衡点．取节点n=3，分别作如图1所示结构的两个模型，符号|→表示抑制作用，→表示催化作用．首先对于图1(a)，3个节点的网络模型为：

(11)

图1 两种基因调控网络模型结构

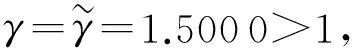
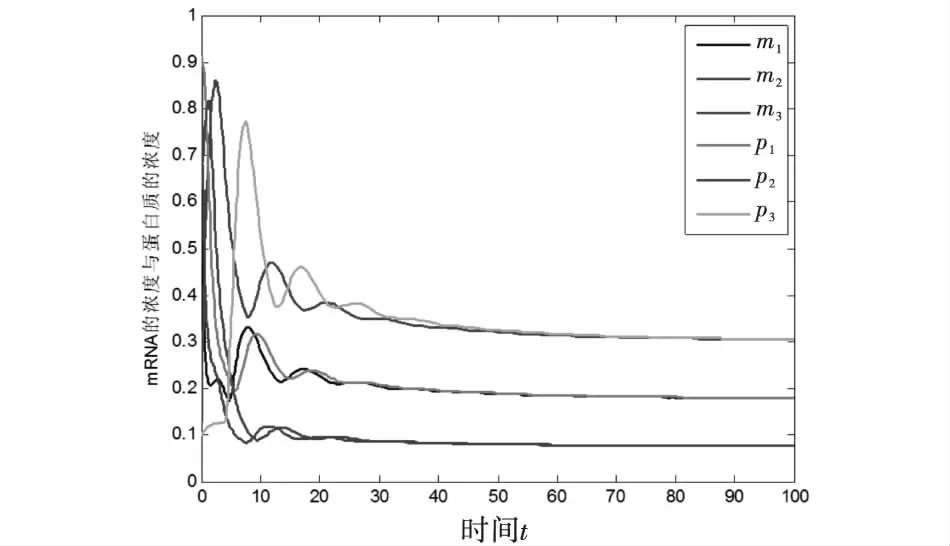
图2 图1(a)结构模型的基因mRNA浓度与蛋白质浓度随时间t的变化曲线

由图2可知，随着时间的变化，系统状态逐渐趋于稳定．对于图1(b)，3个节点的网络模型为：

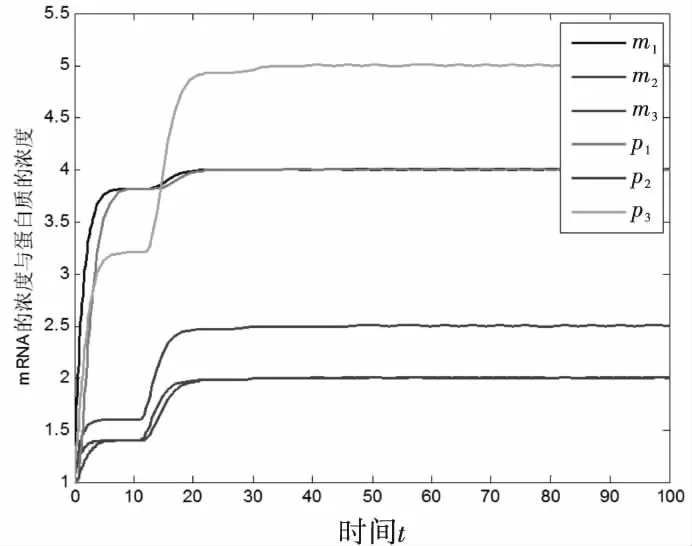
图3 图1(b)结构模型的基因mRNA浓度与蛋白质浓度随时间t的变化曲线

由图3可看出，最终系统状态重合成4条曲线然后达到稳定状态．

4 结 论

参考文献：

[1] Fengli Ren, Jinde Cao. Asymptotic and Robust Stability of Genetic Regulatory Networks with Time-varying Delays[J]． Neurocomputing, 2008，71：834-842．

[2] Guang Ling, Zhihong Guan, Dingxin He, et al. Stability and Bifurcation Analysis of New Coupled Repressilators in Genetic Regulatory Networks with Delays[J]． Neural Netw., 2014，60：222-231．

[3] Chengdai Huang, Jinde Cao, Min Xiao. Hybrid Control on Bifurcation for a Delayed Fractional Gene Regulatory Network[J]． Chaos, Solitons and Fractals, 2016，87：19-29．

[4] 刘 艳. 基因调控网络分析和重建[D]．南京：南京理工大学, 2004：1-3．

[5] FangXiang Wu. Delay-independentent Stability of Genetic Regulatory Networks[J]． IEEE Trans on Neural Netw., 2011，22(11)：1685-1687．

[6] FangXiang Wu. Stability and Bifurcation of Ring-structured Genetic Regulatory Networks with Time Delays[J]． IEEE Trans on Circuits and Systems-I：Regular Papers, 2012，59(6)：1312-1315．

[7] Guang Ling, Zhi-Hong Guan, Rui-Quan Liao, et al. Stability and Bifurcation Analysis of Cyclic Genetic Regulatory Networks with Mixed Time Delays[J]． SLAM J.Applied Dynamical systems, 2015，14(1)：202-220．

[8] Hyung Ju Hwang, Juan J. L. Velzquez. Bistable Stochastic Biochemical Networks：Highly Specific Systems with Few Chemicals[J]． J Math Chem.， 2013，51：1343-1375．

[9] Michael B. Elowitz, Stanislas Leibler. A Synthetic Oscillatory Network of Transcriptional Regulators[J]． Nature, 2000，403：335-338．

[10] Luonan Chen. Stability of Genetic Regulatory Networks with Time Delay[J]． IEEE Trans on Circuits and Systems-I：Fundamental Theory and Applications, 2002，49(5)：602-606．

[11] Zhengxia Wang, Guodong Liu, Yanhong Sun, et al. Robust Stability of Stochastic Delayed Genetic Regulatory Networks[J]． Cogn Neurodyn, 2009(3)：271-280．

[12] Guopeng Zhou, Jinhua Huang, Fengxia Tian, et al. Sufficient and Necessary Conditions for Lyapunov Stability of Genetic Networks with SUM Regulatory Logic[J]． Cogn Neurodyn, 2015(9)：447-458．

[13] Stephen Boyd. Subharmnic Functions and Performance Bounds on Linear Time-invariant Feedback Systems[J]． IMA Journal of Mathematical Control & Information, 1985(2)：153-170．

[14] 王萼芳,石生明.高等代数[M]．4版．北京：高等教育出版社,2015：193-204．