自由边界问题的重心插值迭代配点法研究
赵岳月,王兆清,*,李金
(1.山东建筑大学 工程力学研究所,山东 济南250101;2.山东建筑大学 理学院,山东 济南250101)
0 引言
许多工程问题都可以转化为自由边界问题求解,如自由边界随时间变化时水的融化和凝固问题[1](典型的 Stefan问题[2])、气体在多孔介质中的吸收和扩散(氧气通过生物薄膜的吸收和扩散问题[3]);以及自由边界值不随时间变化的岩土体的无压渗流面问题[4-6]等。自由边界问题一般采用微分方程描述,考虑一类控制方程为二阶线性微分方程的自由边界问题(未知边界为固定值),其形式由式(1)表示为

式中:p(x)、q(x)、f(x)在[a,bf]上连续可导;bf和y(x)未知。求解自由边界问题的难点在于微分方程的求解区域的部分边界是待定的,其待定边界bf要作为解的一部分来求。
为使自由边界问题有解,在自由边界上一般给定过约束边界条件。其中一个边界条件用于求解微分方程,另一个边界条件用于确定自由边界位置。自由边界位置的计算精度依赖于所选择的数值计算方法。有限差分法[7-9]和有限元方法[10-11]是2种经典的求解微分方程自由边值问题的数值方法,其计算精度依赖于差分步长 /单元尺寸的大小,要得到问题的高精度解,需要细化计算网格。自适应投影方法将自由边界问题用有限差分格式离散为一个线性互补问题,在投影迭代过程中自动调整参数[12];改进的插值型边界无单元法不仅要循环积分,还需要计算边界节点上的插值型最小二乘法的形函数矩阵[13],其计算相对比较复杂且计算节点较多。谱Tau方法是一种高精度数值计算自由边界问题的数值方法[14],选取较少的节点计算得到了高精度的数值解。重心插值配点法则采用重心型插值函数作为未知函数的近似函数,利用重心插值微分矩阵可以直接得到微分方程的配点法离散计算矩阵[15]。重心插值配点法具有类似谱方法的计算精度。
文章给定一个自由边界初始假设值,采用重心插值配点法求解微分方程,利用自由边界上的任意一个定界条件构造出确定自由边界位置的2种迭代格式,即Newton法和弦截法,提出了数值求解自由边值问题的重心插值迭代配点法,并以数值算例进行分析,验证了迭代配点法对于自由边界问题求解的可行性和精确性。
1 自由边值问题的重心插值迭代配点法建立
1.1 边值问题的重心插值配点法
将微分方程(1)的未知函数近似为重心插值型多项式 xi,为区间[a,b]上按第二类切比雪夫(Chebyshev)节点分布离散的N个节点,在此节点上的重心插值由式(2)[15]表示为
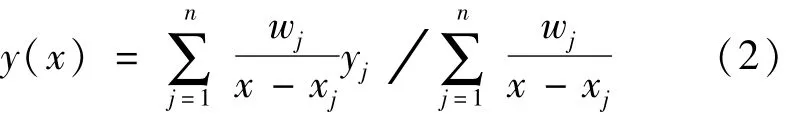
式中:wj为插值权其中j=1,2,…,N。
近似插值函数利用微分矩阵离散的形式由式(3)表示为

式中:P = diag[p(xi)];Q = diag[q(xi)];y =[y(xi)]T;f=[f(xi)]T;P、Q为对角矩阵;y、f为列向量;I为n阶单位矩阵;D(m)为未知函数的m阶插值微分矩阵[10]。
将边界条件利用微分矩阵离散后施加到式(3)中,求解近似函数y(x)。边界条件的施加方法有消去法、置换法、附加法。为了方便处理边界条件,选用了置换法。
1.2 自由边值问题的重心插值迭代配点法
求边值问题需要先假设一个bf的值,以式(1)的自由边界问题为例,y(bf)和 y′(bf)任意与 y(a)构成边值问题的边界条件,bf由第三个条件确定。假设值一般不是真值,于是采用迭代法逼近准确值,文章引进2种迭代格式Newton法和弦截法以满足计算方法的普遍适用性。
1.2.1 Newton迭代格式
(1)当施加的边界条件为第一类边界条件,判定条件为自由边界的导数值时,将近似函数的导函数在bf处(设bf是准确值b*f的近似值)按泰勒公式展开,由式(4)表示为
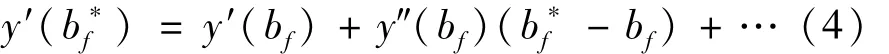
当 y″(bf)≠0时,有于是得到了由y′判定的Newton迭代公式,由式(5)表示为
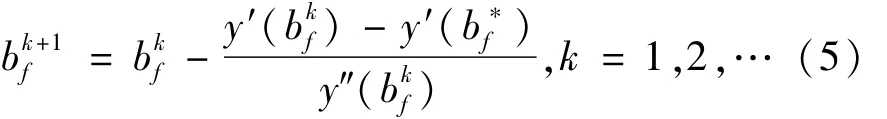
式中为第k+1次迭代得到的自由边界值;为k次得到的自由边界值;y′()为利用的值插值得到的近似函数的导函数在处的值;y″()为近似函数在bkf处的二阶导数值。
(2)当施加的边界条件为混合边界条件,判定条件为自由边界的函数值时,类似于(1)的推导,将近似函数在bf处泰勒展开为bf)+…,得到由y判定的Newton迭代格式,由式(6)表示为
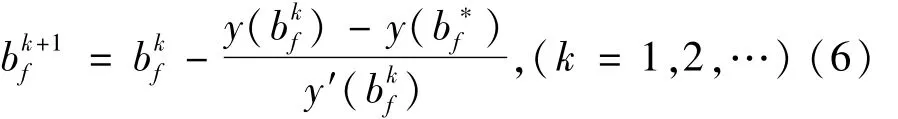
由于计算近似函数时已经将边界条件的一阶导数值施加到了微分方程中,那么y′()为已知的定值,可能会造成计算中迭代不收敛,且当y′()=0时,迭代格式无意义。于是引进了另一种迭代格式弦截法。
1.2.2 弦截法迭代格式
将式(6)中近似函数 y(x)在点处的切线斜率y′()改用曲线上2点弦的斜率代替,即得到由y判定的弦截法迭代格式,由式(7)表示为
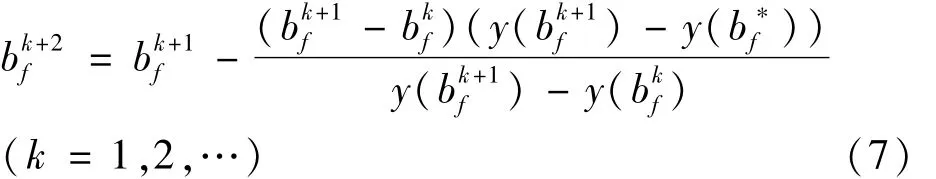
式中分别为第 k+2、k+1、k次迭代得到的自由边界值是利用的值插值得到的近似函数在处的值。
弦截法的迭代格式中要得到的值需要有第k+1次的的值第k次的的值,所以在计算过程中要假设2个初始值。在计算中直接令,则那么在此迭代格式中只需要假设一个初始值。
同样地,将式(4)中y″()也改用曲线上2点弦的斜率代替,得到y′判定的弦截法迭代格式,由式(8)表示为

1.2.3 重心插值配点法的迭代步骤
(1)令 k=1,且 k≤100,假设的 b′f值,(弦截法令=a,假设的值);
(2)将求解区域[a](弦截法离散成N个节点;用式(2)、(3)计算第k次近似函数yk,得到的值,其中。(在弦截法中
(3)用迭代公式(7)计算第k+1次的自由边界值(弦截法用式(5)计算第k+2次的自由边界
值)和的值;
(4)Newton法用 y′()作为判定条件,若则重复过程(2)和(3);若k>100,解不收敛,跳出循环;若 y′()<ε,迭代结束,输出、yk。为所求自由边界的近似值;yk为在边界[a]上的近似函数。
(5)弦截法用作为判定条件,若,重复过程(2)和(3);若k>100,解不收敛,跳出循环;若,迭代结束,输出为所求自由边界的近似值,yk+1为在边界上的近似函数。
2 数值算例验证
数值算例的计算程序利用MATLAB编写,其中m为自由边值的迭代次数,N为插值节点的数量。
2.1 算例1
二阶线性微分方程的自由边值问题[14]。
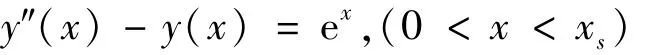
边界条件为

问题的解析解为
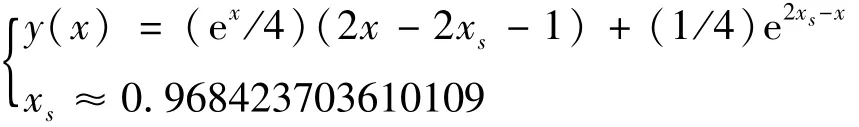
在问题求解中将y(0)=1和y(xs)=0作为边界条件,y′(xs)=0作为判定条件,采用2种迭代格式来计算,比较其迭代次数和误差精度,误差的控制精度为10-10。假设初始边界为xs=1,其结果见表1和2。

表1 Newton法迭代配点表
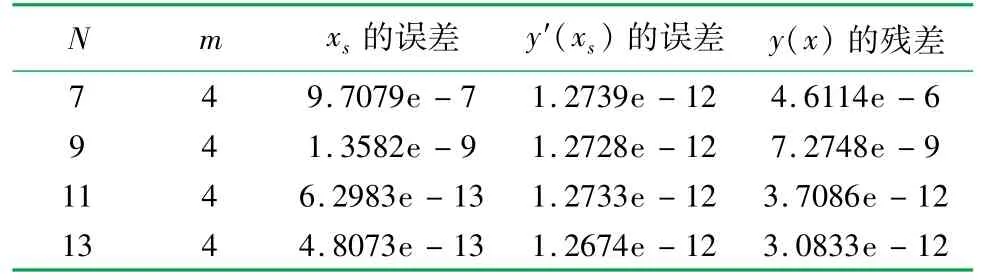
表2 弦截法迭代配点表
由表1和2可知,2种方法求解微分方程的自由边界问题时,均得到了10-11~10-13量级的高精度解。在边界条件和节点数量相同的情况下,Newton迭代法要比弦截法的收敛速度快,只需要迭代3、4次就可以得到满足控制误差精度的解。而对于xs和近似函数y(x)的误差弦截法要稍稍优于Newton法约10-2,但是在实际计算中Newton法的计算精度足以满足微分方程的计算要求。
2.2 算例2
线性微分方程自由边值问题。

边界条件为
问题的解析解为

在问题求解中首先将y(0)=1和y′(xs)=0作为边界条件,y(xs)=0作为判定条件,假设初始边界为xs=1。由于y′(xs)=0,采用Newton迭代格式时无法计算,于是选用弦截法迭代格式。误差的控制精度为10-10,计算结果见表3。而当选取y(0)=1和y(xs)=0作为边界条件,y′(xs)=0作为判别条件时,Newton迭代法和弦截法都可以求解。
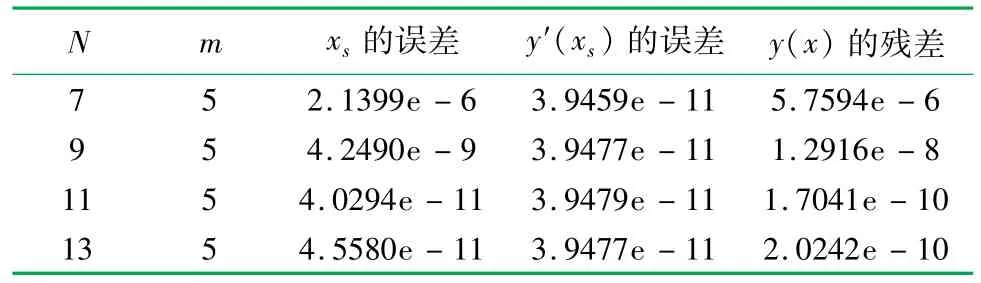
表3 弦截法迭代配点表
3 结论
通过上述算例分析表明,2种迭代格式都可以解线性微分方程的自由边值问题,而且计算精度都很高。
(1)Newton法的迭代速度较弦截法快,迭代3、4次就可以得到高精度的解,且计算公式简单。
(2)由于边界条件以及控制方程自身的原因,可能会造成Newton迭代配点法无法计算,而对弦截法计算无影响,其计算精度与Newton法基本相当,只是在初始值的处理上比较复杂。
(3)重心插值迭代配点法是一种高精度的迭代配点法,在求解线性微分方程自由边界问题时,可以根据问题的特点选取适当的迭代格式。计算误差精度随节点的增加成量级提高,可以达到10-11~10-13。在计算自由边值问题时具有计算公式简单,数值程序实施方便,计算精度高等优点。
参考文献:
[1]Mitchell S L,Vynnycky M,Gusev I G,et al.An accurate numerical solution for the transient heating of an evaporating spherical droplet[J].Applied Mathematics& Computation,2011,217(22):9219-9233.
[2]Borodin M A.Stefan problem[J].Journal of Mathematical Sciences,2011,178(1):13-40.
[3]Bougoffa L.The adomian decomposition method for solving a moving boundary problem arising from the diffusion of oxygen in absorbing tissue[J].The Scientific World Journal,2014,2014:1-7.
[4]王兆清,李术才,李树忱.无压渗流问题分析的多节点有限元方法[J].岩土力学,2008,29(10):2647-2650.
[5]李树忱,王兆清,袁超.岩土体渗流自由面问题的重心插值无网格方法[J].岩土力学,2013(7):1867-1873.
[6]郑珊珊.求解渗流自由面的逐步剖分法[D].烟台:烟台大学,2017.
[7]Kim B J,Ahn C,Choe H J.Direct computation for American put option and free boundary using finite differencemethod[J].Japan Journal of Industrial&Applied Mathematics,2013,30(1):21-37.
[8]Devi P K,Naidu V G.A new finite difference front tracking method for two phase 1-D moving boundary problems[J].Procedia Engineering,2015,127:1034-1040.
[9]林鸿熙,宋丽平,江良.美式期权自由边界的计算方法[J].数学的实践与认识,2014,44(24):141-145.
[10]Gawlik E S,Lew A J.Unified analysis of finite elementmethods for problems with moving boundaries[J].Siam Journal on Numerical Analysis,2015,53(6):2822-2846.
[11]邓建霞.有自由面渗流分析的加密高斯点单元传导矩阵调整法[D].成都:四川大学,2004.
[12]钟艳丽,严月月,钟思超,等.求解自由边界问题的自适应投影方法[J].重庆工商大学学报(自然科学版),2017(5):7-12.
[13]余春君.Signorini问题的无网格投影迭代算法[D].重庆:重庆师范大学,2016.
[14]AliabadiM H,Ortiz E L.Numerical treatment ofmoving and free boundary value problems with the tau method[J].Computers&Mathematics with Applications,1998,35(8):53-61.
[15]李树忱,王兆清.高精度无网格重心插值配点法——算法、程序及工程应用[M].北京:科学出版社,2012.

