基于极线几何的统计优化特征匹配算法

赵春晖，樊斌，田利民，胡劲文，潘泉

西北工业大学 自动化学院，西安 710072

视觉同时定位与构图(SLAM)的初始化阶段需要利用特征匹配进行三角化得到3D点云[1-2]，特征匹配的准确率和召回率的高低直接影响着3D点云的数量和3D坐标的准确性，进而影响相机位姿的估计精度。

BF(Brute Force)算法[3]通过计算2幅图像特征点描述子之间的欧式距离，找到最接近的特征点作为候选匹配。但是，由于虚假的检测，最接近的特征点可能不是真正匹配的特征点。为解决该问题，FLANN(Fast Library for Approximate Nearest Neighbors)算法[4-5]被提出。它利用比率测试来验证候选匹配特征点对，以剔除虚假匹配。但存在2个主要问题：① 高分辨率图像的特征点成千上万，对数千个特征点进行描述是一项艰巨的任务；② 特征点随机分布的假设并不适用于具有重复结构的图像，如窗户、农田等。由于相似的外观，比率测试拒绝了许多重复结构的特征点。为解决该问题现已提出了一些解决方案，但需要重复结构共面或特征仿射不变等额外的假设和处理步骤[6-8]。RANSAC (RANdom SAmple Consensus)算法[9-11]可以缓解这些问题,但RANSAC本身要求大多数误匹配应被预先排除,并且当最近距离匹配集合中的误匹配数量较多时会失效。

罗楠等[12]在研究具有重复结构的图像匹配方法时，针对基于局部特征的匹配方法容易出现误匹配以及全局特征点主方向依然通过计算局部特征点相关信息得到等问题，提出了一种基于成对特征点的匹配方法。该方法通过修正特征点的方向信息来提高匹配准确率，启示了本文特征点主方向的研究。刘威等[13]对ORB(Oriented FAST and Rotated BRIEF)特征采用K近邻搜索策略来减少误匹配，利用双向匹配得到初匹配，对初匹配采用比率法，按照比率升序排列，选择前若干个匹配对计算RANSAC的模型参数，再计算所有匹配对的误差和内点数量。该算法利用ORB特征提高计算效率的同时利用最近邻和次近邻的比值作为匹配对质量好坏的判断标准进行筛选，对本文特征点匹配算法的研究提供了很大的参考。Shah等[14-15]选取部分特征点估计基本矩阵，利用对极约束计算每个特征点在目标图中的极线，利用二维图像网格化划分搜索区域以确定候选匹配，最后利用RANSAC去除误匹配。该算法利用部分特征点计算基本矩阵的思想值得借鉴。

许多特征匹配方法首先使用全局比率测试，然后采用对极约束验证[16-19]，这样会先发地拒绝许多重复结构的特征。本文认为，如果在比率测试之前使用对极约束，那么在重复结构上可以保留较多真实的匹配。此外，Sampson距离用于基本矩阵的估计时更为简单，且对极约束模型的高阶项相对一阶项较小的时候近似效果会更好[1,20-21]。因此，本文提出了一种基于极线几何的统计优化特征匹配算法。正确匹配的特征点之间满足对极约束，它同样适用于具有重复结构的图像，而不需要任何假设或复杂的处理。由于基本矩阵的估计需要正确的特征匹配，首先,通过可靠地匹配2幅图像的特征点子集，利用基于Sampson距离的RANSAC算法来估计2幅图像之间的基本矩阵；然后，利用对极约束模型优化正确匹配点的大致区域，从而避免由于重复结构增加的误匹配对，减小特征点搜索区域；最后，利用基于特征点主方向和尺度信息的统计优化算法，得到最终匹配结果。

1 本文所提算法

本文算法首先通过可靠地匹配2幅图像的尺度不变特征转换(Scale Invariant Feature Transform,SIFT)特征子集，估计2幅图像之间的基本矩阵并作为先验信息。然后对原图中每一个特征点，利用对极约束优化正确匹配点的大致区域，采用KD(K-Dimension)树搜索出对应匹配点，并利用双向匹配反向验证得到初匹配。对于初匹配，再进一步利用基于特征点尺度和主方向信息的统计优化方法消除误匹配，得到更精确的匹配结果。算法流程图如图1所示。

图1 提出的算法流程图Fig. 1 Flow chart of proposed algorithm

1.1 算法步骤及原理

步骤1基本矩阵的估计。首先，提取SIFT特征点，利用双向FLANN匹配方法得到可靠匹配对；然后，利用基于Sampson距离的RANSAC算法估计基本矩阵F。

基于Sampson距离的RANSAC算法为：每次随机不重复地选择8组匹配对，利用归一化8点算法[1]计算基本矩阵F，并分别计算所有的匹配对与对极约束模型之间的Sampson距离，如式(7)所示，若小于阈值，则加入内点集合。经过多次迭代，选择内点数量最多的集合为最终内点集合，并利用该内点集合结合RANSAC算法估计基本矩阵F。

基本矩阵F是一个3×3的矩阵，有8个自由度，每对匹配点只能得到一个方程，因此计算F至少需要8个匹配对。

构造极线约束的代价函数:

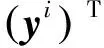
(1)

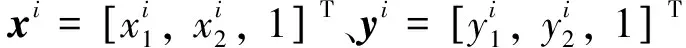
利用泰勒展开式作一阶逼近：

(2)

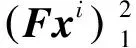
(3)

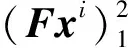
JΔX=-CF(X)

(4)

f(ΔX)=ΔXTΔX-2λ(JΔX+CF(X))

(5)

求解可得

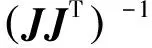
(6)

结合式(3)，可得Sampson距离为

(7)

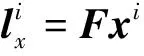
(8)

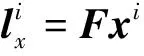
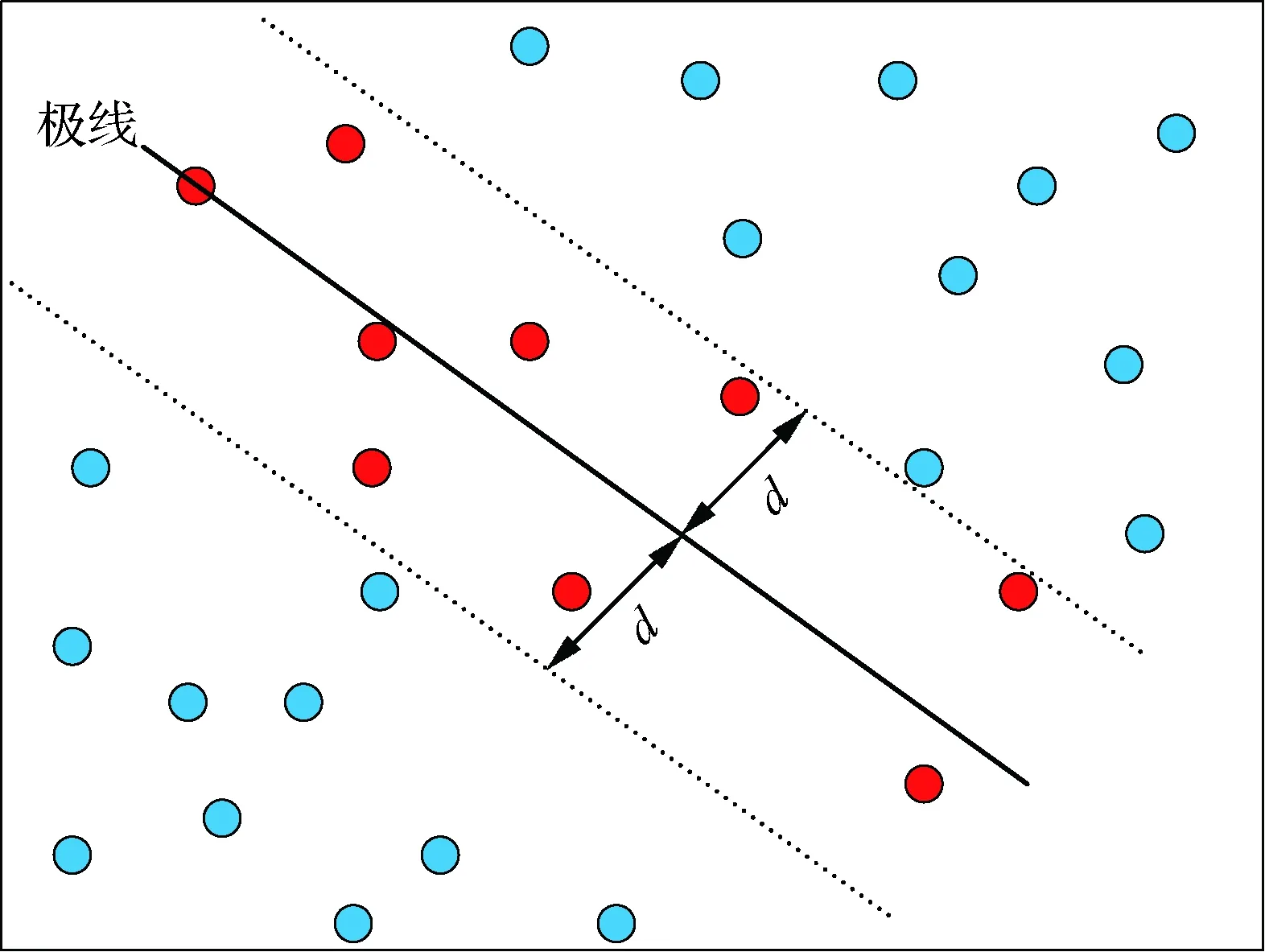
图2 极线搜索示意图Fig.2 Schematic diagram of epipolar search

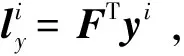
步骤4为了得到更为精确的匹配结果，本文利用基于特征点主方向和尺度信息的统计优化方法进一步消除误匹配。对于步骤1～步骤3得到的初匹配结果，每次随机选取一定比例的初匹配结果计算匹配主方向差和尺度比的标准差，若匹配主方向差的标准差大于某阈值，则去除其中的离群值对应的匹配对；若匹配尺度比的标准差大于某阈值，则去除其中的离群值对应的匹配对，不断迭代，最终得到更加精确的匹配结果。

综上，本文算法利用对极约束为每个特征点构造了一个较小的待匹配特征点集合，并基于特征点主方向和尺度信息进一步优化匹配结果。而对于原图某一特征点，传统特征匹配方法中的待匹配特征点集合是目标图的所有特征点，此时当在极线外存在与其结构重复的特征点时，传统方法可能会匹配错误。因此本文算法可以减少搜索范围和重复结构的错误拒绝，而且基于特征点主方向和尺度信息可以对初匹配结果进一步优化。

1.2 基于特征点主方向和尺度信息的统计优化

假设提取的某SIFT特征点位置为(x,y)，尺度为σ，如图3(a)所示，则该特征点所在的尺度图像为

L(x,y)=G(x,y,σ)*I(x,y)

(9)

式中：*表示卷积；I(x,y)为图像区域；G(x,y,σ)为高斯核函数，满足:

(10)

使用有限差分计算以(x,y)为中心、3×1.5σ为半径的邻域内每个像素L(x,y)对应梯度的幅值和幅角，即

(11)

利用梯度直方图统计该邻域内所有像素的梯度分布特性，其横轴是梯度幅角(将0°～360°的范围分为36个柱，每10°一个柱，共36个柱)，纵轴是梯度幅角对应的梯度幅角个数，如图3(b)所示。最后，通过对直方图中主峰值和距离它最近的2个柱值进行抛物线插值得到该特征点的主方向θ。

图4为匹配主方向差的定义示意图。图4中：θL为原图中的特征点fL(实线箭头)的主方向；σL为原图对应尺度；θR为目标图中匹配特征点fR(虚线箭头)的主方向；σR为目标图对应尺度。即

θ1=θL

(12)

θ2=(θL+180°)%360°

(13)

定义1匹配主方向差为2个已匹配特征点的主方向之间的夹角α。若目标图中匹配特征点的主方向位于区域A，则α>0；若目标图中匹配特征点的主方向位于区域B，则α<0。如图4所示，即

1) 0°≤θL<180°

(14)

2) 180°≤θL<360°

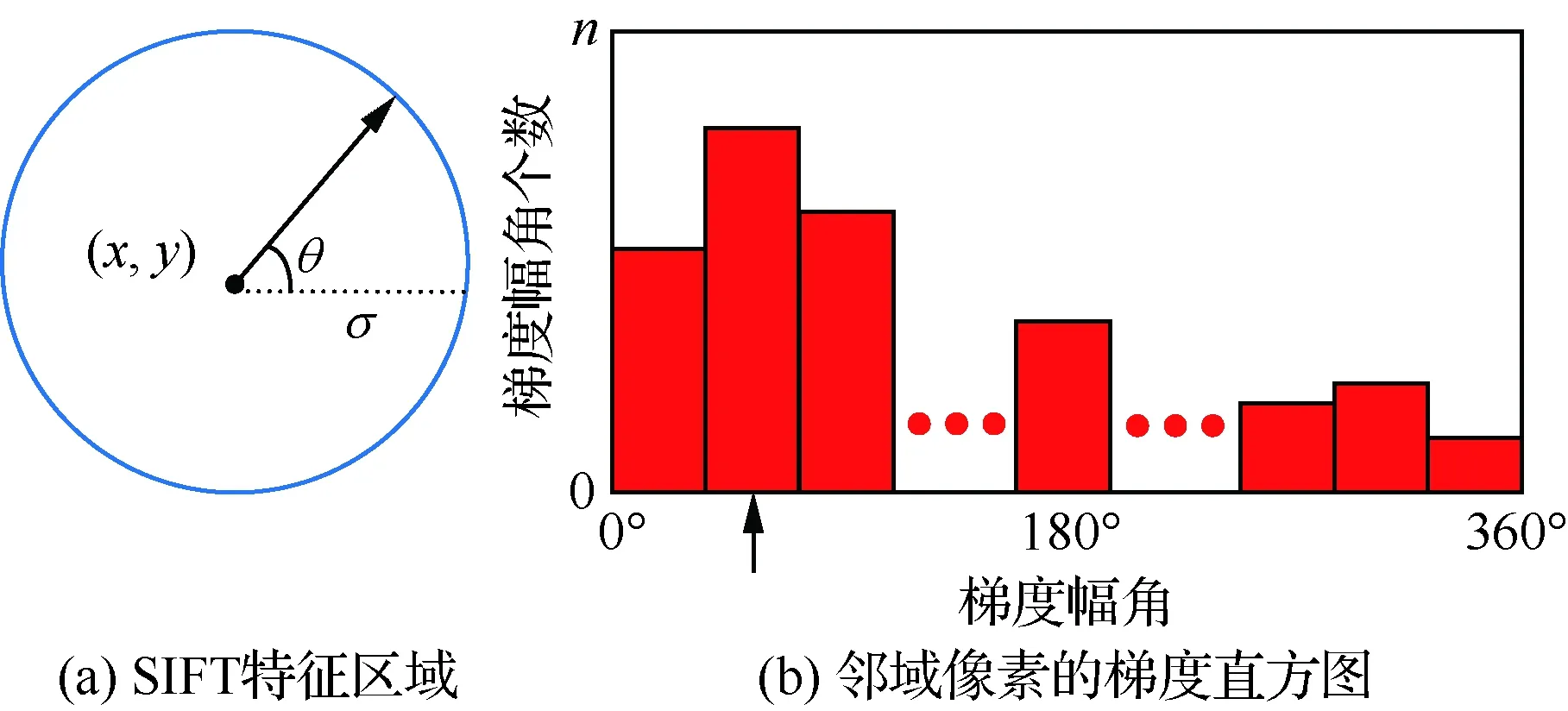
图3 SIFT主方向的定义示意图Fig.3 Schematic diagram of definition of SIFT main direction

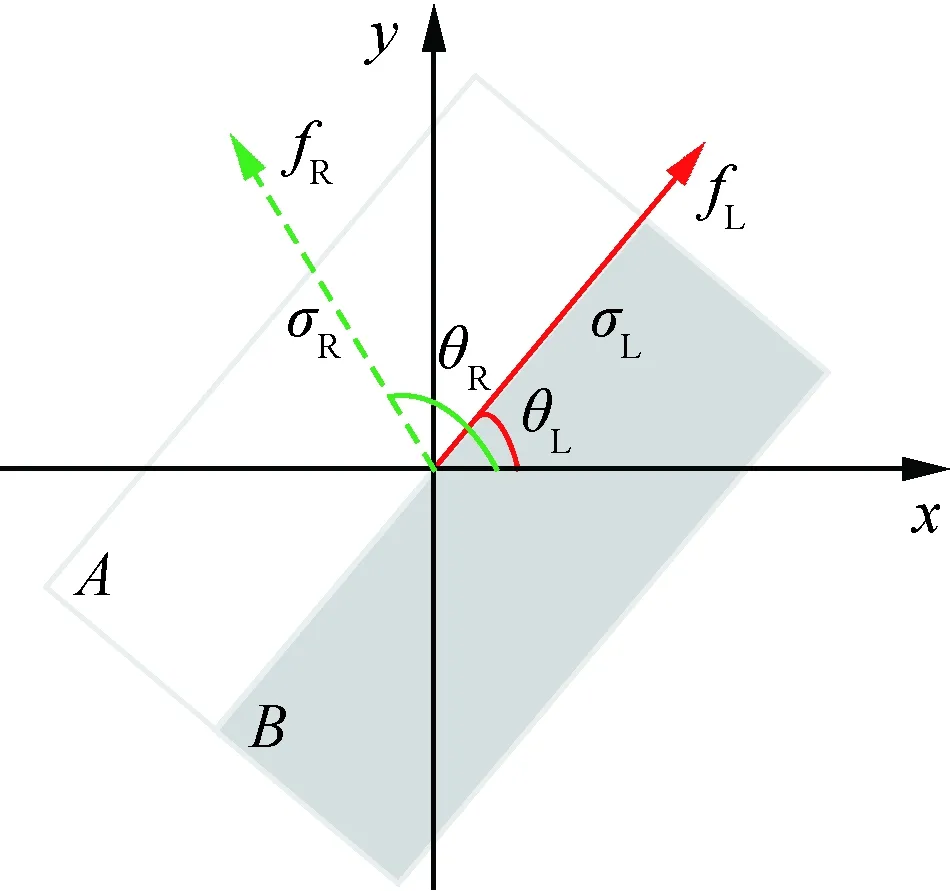
图4 匹配主方向差的定义示意图Fig.4 Schematic diagram of definition of main direction difference

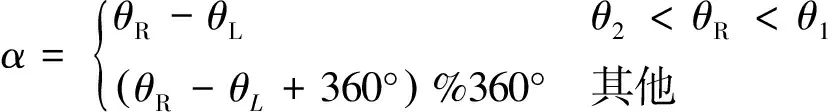
(15)

定义2匹配尺度比为原图中的特征点的尺度与目标图中匹配特征点尺度的比值,即

(16)

由定义1可知，匹配主方向差的范围为-180°～180°。本文采用TUM数据集[22]的freiburg3_long_office_household中的视频序列图片，通过大量实验分析匹配主方向差和尺度比在已匹配特征点对上的分布情况。

分别将目标图逆时针旋转90°和缩放0.5倍后与原图匹配，对匹配点对的尺度比和主方向差进行测试，如图5所示，其中红色为无旋转和缩放变换，蓝色为旋转变换，绿色为缩放变换。

分别将数据集中第0帧与第0,1,…,99帧用BF、FLANN、ROBUST算法进行匹配，统计匹配主方向差和尺度比的标准差的分布，如图6和图7所示。

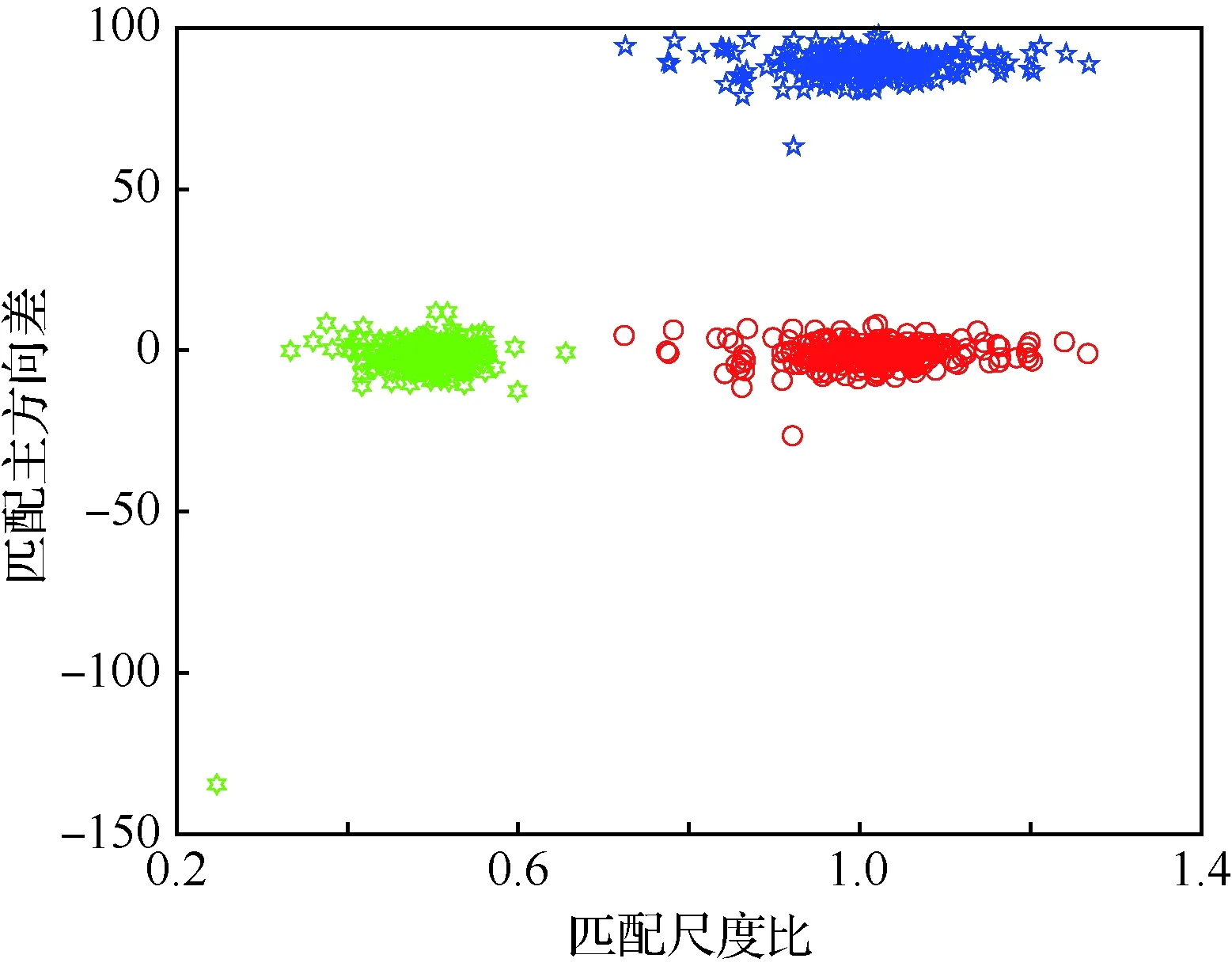
图5 匹配点对的尺度比和主方向差的分布Fig.5 Distribution of scale ratio and main direction difference of matching features

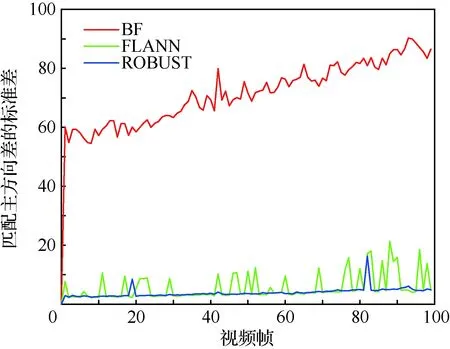
图6 匹配主方向差的标准差的分布Fig.6 Distribution of standard deviation of main direction difference of matching

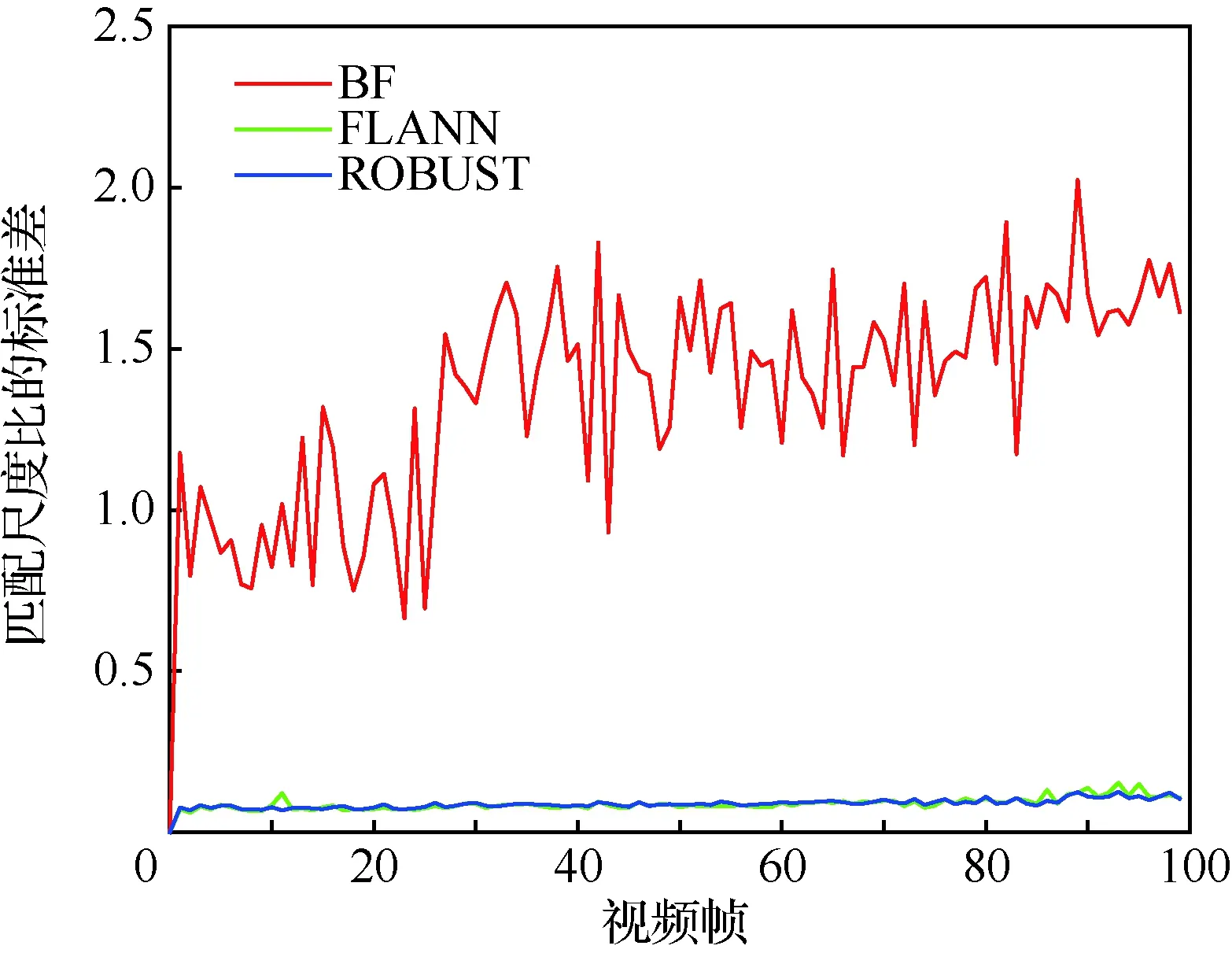
图7 匹配尺度比的标准差的分布Fig.7 Distribution of standard deviation of scale ratio of matching

由图5可知，匹配主方向差和尺度比的分布较为集中，但同时也存在少量的孤立点和离群值，这是因为存在误匹配。

由于BF匹配结果中存在大量误匹配，即BF匹配主方向差和匹配尺度比中存在大量离群值； FLANN和ROBUST匹配结果中误匹配较少，其中的离群值相对较少。结合图6和图7可知，正确匹配对的匹配主方向差和尺度比的标准差较小，分布较为集中，因此可以利用匹配主方向差和匹配尺度比的标准差判断初匹配结果是否正确。即，每次从初匹配结果中随机选取部分匹配结果，计算其匹配主方向差和尺度比的标准差，若匹配主方向差的标准差大于某阈值，可以去除其中的离群值对应的匹配以消除误匹配；若匹配尺度比的标准差大于某阈值，可以去除其中的离群值对应的匹配以消除误匹配。

2 实验和结果

本实验采用Ubuntu 14.04平台，基于OpenCV搭建Cmake工程。实验选取TUM[22]和DTU[23]数据集，如表1所示。实验阈值设置如表2所示。实验原图和目标图如图8所示，分别包含模糊、视角变化、光照变化和低纹理等噪声。

每组实验的实验环境分为3部分：原图像分别与目标图像(场景1)、目标图像顺时针旋转90°(场景2)、目标图像缩放0.5倍(场景3)进行匹配测试，实验结果如表3所示。

表1 数据集简介Table 1 Introduction of data sets

表2 实验阈值设置Table 2 Experimental threshold setting

图8 实验图像Fig. 8 Images for experiment

结合表3，从图9可以看出对于重复结构下的匹配，本文算法匹配数量更多。图10和图11的匹配结果表明本文方法对图像的旋转和缩放变换具有良好的鲁棒性。由表3中各种实验环境下的算法比较可知，本文算法的匹配数量约是FLANN和ROBUST算法的1.2倍，匹配准确率平均提高了1%左右；实验5的结果也表明对于具有重复结构的图像间的匹配，本文算法的匹配数量和准确率都有很大的提升。

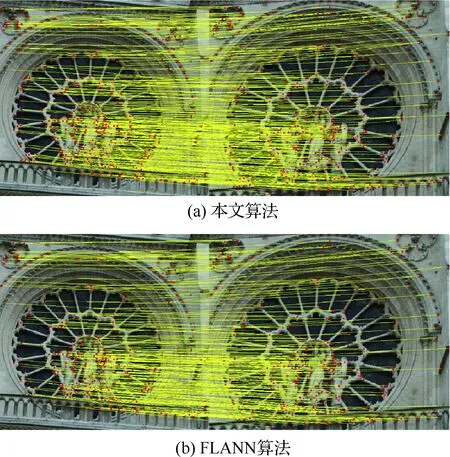
图9 实验5重复结构下的匹配结果Fig.9 Experiment 5 matching result in repetitive structure

表3 本文算法与FLANN和ROBUST匹配算法的性能比较Table 3 Comparison of performance of proposed algorithm, FLANN and ROBUST matching algorithms

图10 实验2匹配结果Fig.10 Mathing results of Experiment 2

图11 实验4匹配结果Fig.11 Matching results of Experiment 4

3 结 论

1) 本文算法对图像的旋转和缩放变换具有良好的鲁棒性，匹配数量达到了FLANN和ROBUST算法的1.2倍左右，匹配准确率平均提高了1%左右，并且也能较好地处理具有重复结构的图像间的匹配。

2) 本文算法的时间复杂度为O(kn2)，计算量相对较大，如何提高本文算法的运行效率和处理严重重复结构的能力将是接下来的研究目标。

参 考 文 献

[1] HARTLEY R, ZISSERMAN A. Multiple view geometry in computer vision[M]. Cambridge: Cambridge University Press, 2003: 191-215.

[2] MUR-ARTAL R, MONTIEL J M M, TARDOS J D. ORB-SLAM: A versatile and accurate monocular SLAM system[J]. IEEE Transactions on Robotics, 2015, 31(5): 1147-1163.

[3] ARYA S, MOUNT D M. Approximate nearest neighbor queries in fixed dimensions[C]∥SODA’93: Proceedings of the Fourth Annual ACM-SIAM Symposium on Discrete Algorithms. Philadelphia, PA: Society for Industrial and Applied Mathematics, 1993: 271-280.

[4] LOWE D G. Distinctive image features from scale-invariant key points[J]. International Journal of Computer Vision, 2004, 60(2): 91-110.

[5] MUJA M, LOWE D G. Fast approximate nearest neighbors with automatic algorithm configuration[J]. International Conference on Computer Vision Theory and Applications (VISAPP), 2009, 2(1): 331-340.

[6] KUSHNIR M, SHIMSHONI I. Epipolar geometry estimation for urban scenes with repetitive structures[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2014, 36(12): 2381-2395.

[7] ZHANG W, KOSECKA J. Generalized RANSAC framework for relaxed correspondence problems[C]∥Third International Symposium on 3D Data Processing, Visualization, and Transmission. Piscataway, NJ: IEEE Press, 2006: 854-860.

[8] SUR F, NOURY N, BERGER M O. Image point correspondences and repeated patterns[J]. Computer Vision & Pattern Recognition, 2011, 8(2): 216-243.

[9] FISCHLER M A, BOLLES R C. Random sample consensus: A paradigm for model fitting with applications to image analysis and automated cartography[J]. Communications of the ACM, 1981, 24(6): 381-395.

[10] CHIN T J, YU J, SUTER D. Accelerated hypothesis generation for multi-structure data via preference analysis[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2012, 34(4): 625-638.

[11] 王云丽, 张鑫, 高超, 等. 航拍视频拼图中基于特征匹配的全局运动估计方法[J]. 航空学报, 2008, 29(5): 1218-1225.

WANG Y L, ZHANG X, GAO C, et al. The global motion estimation method based on feature matching in video[J]. Acta Aeronautica et Astronautica Sinica, 2008, 29(5): 1218-1225 (in Chinese).

[12] 罗楠, 孙权森, 陈强, 等. 针对重复模式图像的成对特征点匹配[J]. 中国图象图形学报, 2015, 20(1): 113-124.

LUO N, SUN Q S, CHEN Q, et al. Pair-wise feature points based matching algorithm for repetitive patterns images[J]. Journal of Image and Graphics, 2015, 20(1): 113-124 (in Chinese).

[13] 刘威, 赵文杰, 李德军, 等. 一种基于ORB检测的特征点匹配算法[J]. 激光与红外, 2015, 45(11): 1380-1384.

LIU W, ZHAO W J, LI D J, et al. Feature points matching algorithm based on ORB detection[J]. Laser and Infrared, 2015, 45(11): 1380-1384 (in Chinese).

[14] SHAH R, SRIVASTAVA V, NARAYANAN P J. Geometry-aware feature matching for structure from motion applications[C]∥2015 IEEE Winter Conference on Applications of Computer Vision (WACV). Piscataway, NJ: IEEE Press, 2015: 278-285.

[15] SHAH R, DESHPANDE A, NARAYANAN P J. Multistage SFM: Revisiting incremental structure from motion[C]∥2014 2nd International Conference on 3D Vision (3DV). Piscataway, NJ: IEEE Press, 2014: 417-424.

[16] ZHANG Z, DERICHE R, FAUGERAS O, et al. A robust technique for matching two uncalibrated images through the recovery of the unknown epipolar geometry[J]. Artificial Intelligence, 1995, 78(1-2): 87-119.

[17] 陈洁, 高志强, 密保秀, 等. 引入极线约束的SURF特征匹配算法[J]. 中国图象图形学报, 2016, 21(8): 1048-1056.

CHEN J, GAO Z Q, MI B X, et al. SURF feature matching based on epipolar constraint[J]. Journal of Image and Graphics, 2016, 21(8): 1048-1056 (in Chinese).

[18] 李立春, 张小虎, 傅丹, 等. 基于极线局部校正的特征匹配方法[J]. 光学技术, 2008, 34(2): 285-288.

LI L C, ZH X H, FU D, et al. Feature matching algorithm based on rectification of epipolar-line region[J]. Optical Technique, 2008, 34(2): 285-288 (in Chinese).

[19] 张培耘, 华希俊, 夏乐春, 等. 基于 RANSAC 算法的极线约束立体视觉匹配方法研究[J]. 组合机床与自动化加工技术, 2013(11): 20-22.

ZHANG P G, HUA X J, XIA L C, et al. Stereo matching with epipolar line constraints based on RANSAC algorithm[J]. Modular Machine Tool & Automatic Manufacturing Technique, 2013(11): 20-22 (in Chinese).

[20] 单欣, 王耀明, 董建萍. 基于RANSAC算法的基本矩阵估计的匹配方法[J]. 上海电机学院学报, 2006, 9(4): 66-69.

SHAN X, WANG Y M, DONG J P. The matching method based on RANSAC algorithm for estimation of the fundamental matrix[J]. Journal of Shanghai Dianji University, 2006, 9(4): 66-69 (in Chinese).

[21] 田谨思, 苏剑波. 基于Sampson误差计算单应的立体匹配[J]. 计算机工程与应用, 2005, 41(3): 7-9.

TIAN J S, SU J P. Stereo matching with epipolar line constraints based on RANSAC algorithm[J]. Computer Engineering and Applications, 2005, 41(3): 7-9 (in Chinese).

[22] STURM J, ENGELHARD N, ENDRES F, et al. A benchmark for the evaluation of RGB-D SLAM systems[C]∥2012 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS). Piscataway, NJ: IEEE Press, 2012: 573-580.

[23] AANAES H, DAHL A L, PEDERSEN K S. Interesting interest points[J]. International Journal of Computer Vision, 2012, 97(1): 18-35.