超声速细长飞行器前置小翼展开过程的非定常特性
唐海敏,杜厦,傅建明,李欣益
上海机电工程研究所,上海 201109
现代战争中,拦截用飞行器是拦截、攻击空中移动目标的重要武器。随着新技术革命浪潮的涌入,空中目标的速度越来越大、机动能力愈来愈高,拦截用飞行器的作战性能随之面临新的挑战:一方面需要具有较快的飞行速度,另一方面需要其在飞行末端命中目标前很短时间内具有快速改变飞行轨迹和飞行姿态的能力,即在该时段内具有非常强的机动性,以提高拦截成功率。
为应对上述新的性能要求,日前主要采用姿态控制侧向直接力方案和轨迹控制侧向直接力方案。但这两种方案因涉及侧向力发动机布置使系统和结构更加复杂,侧向喷流与来流相互干扰产生的复杂波涡结构[1-6]使飞行器总体气动特性甚至舵面效率变化随参数呈现更强的非线性[4],侧向力发动机燃料受限使控制时间较短,增加了侧喷控制方案的设计和使用难度。为此,考虑在飞行器头部附近加装可展开的前置小翼,在需要时前置小翼快速伸出产生气动力及控制力矩,实现对飞行器姿态和轨迹的控制。前置小翼伸出之后,飞行器的法向力系数增加,提高了气动过载,压心前移,降低了静稳定度,从而使飞行器的机动性增强。
小翼在展开过程中绕飞行器的流动及飞行器本身所受气动力都是复杂的非定常问题。翼面展开改变了飞行器的表面形状,高速条件下会诱导出复杂的波系与涡系结构,如翼前激波、翼后分离涡等,同时其诱导产生的下洗流场影响飞行器弹体及后体尾舵的流动特性和载荷,这些流动机理以及翼面展开过程中飞行器气动特性的时变规律,亟需开展详细研究。
本文研究重点是前置小翼在展开过程中波涡等复杂流动结构的形成和发展以及气动特性随时间的变化规律。利用适合翼面展开大变形条件的结构动网格技术以及非定常脱体涡模拟(DES)方法,数值研究了大长细比飞行器上前置小翼展开对飞行器气动特性的影响规律及机理,获得了详细的瞬时流场结构特性,分析了法向力、纵向压心系数随时间的变化特性。结果表明小翼展开对飞行器超声速、大迎角条件控制力和力矩产生了较大的有利增益,是一种提高飞行器机动能力的有效途径。
1 研究外形及条件
图1给出了本文的研究外形,由弹体、尾舵以及4片前置小翼组成,前置小翼为扇形,展开时绕根弦前缘点旋转,最大展开角度为30°,展开角速度为660 (°)/s。图2给出了小翼展开角度φ的定义。计算条件由表1给出,其中滚转角Φ的定义见图3。

图1 模型外形Fig.1 Model geometry

图2 小翼展开角度定义Fig.2 Definition of wing spread angle

表1 来流条件Table 1 Incoming flow conditions
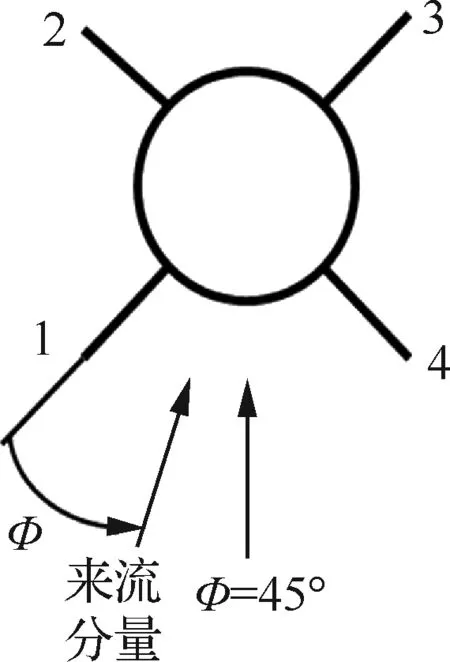
图3 滚转角定义(后视图)Fig.3 Definition of rolling angle (rear view)
2 数值模拟方法
前置小翼展开将诱导产生复杂的非定常波系与涡系结构,准确模拟这种强非定常现象将对数值方法的模拟精度提出更高要求。传统雷诺平均Navier-Stokes(RANS)方法难以准确模拟大范围分离等复杂流动现象,直接数值模拟(DNS)或大涡模拟(LES)方法[7]虽能精确预测但因对计算机硬件能力需求过高仍难以承受,目前可行的途径是采用RANS/LES混合方法[8-15]。RANS/LES混合方法结合了RANS和LES两者各自的优势,在边界层采用RANS方程,在分离区采用LES,计算量比LES少,计算结果比RANS优,效果与LES相当。在当前计算机能力仍较难满足DNS和LES的情况下,混合方法无疑是兼顾效果和效率的选择,在复杂流动问题上,已被证实有很高的可信度[16]。本文采用Spalart等[8]提出的脱体涡模拟,并引入边界层延迟转捩函数抑制模型应力损失。
2.1 空间/时间离散方法
采用三维可压缩Navier-Stokes方程为控制方程,通过有限体积方法进行离散,对流项离散采用二阶精度的Roe格式[17],黏性项离散采用中心差分格式,非定常数值方法时间项离散使用高计算效率的双时间步方法[18-19],内迭代采用LU-SGS[20]隐式方法,并采用局部时间步长方法加速内迭代过程收敛。
2.2 DES模型
DES模型最早由Spalart等[8]于1997年提出,在近壁面采用雷诺平均方法,用湍流模型模拟小尺度脉动,在其他区域,通过对传统湍流模型尺度系数的修正,使模型起到LES亚格子应力模型的作用。DES方法结合了常规RANS方法和LES方法的优点,不仅可以节省时间,而且计算结果准确,尤其是对于大范围分离流动的模拟。
根据其中RANS采用的湍流模型的不同,目前主要有基于Spalart-Allmaras(S-A)[21]湍流模型以及基于Menter剪切应力输运(SST)湍流模型的DES方法[8-15]。
基于S-A模型的DES方法中,湍流涡黏性系数定义为
(1)
式中:

(2)
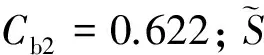
(3)
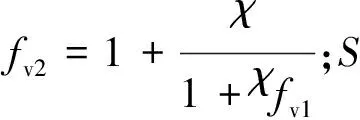
(4)
g=r+Cw2(r2-r)
(5)

(6)
式中:d为流场中空间点到壁面的最近距离;Δ为当地网格单元中心到临近单元中心的最大距离;CDES一般取值0.65。
DES模型对网格分布具有较强依赖性,导致其往往会在边界层内提前开启LES模式。边界层内采用LES模式容易导致计算得到的涡黏性不足,造成非物理的网格诱导分离。为解决这一问题,引入了边界层延迟转捩函数fd[15],重新构造了混合方法长度尺度,可以在边界层内关闭LES模式,这种方法称为延迟脱体涡模拟(DDES)方法。
边界层延迟转捩函数fd的定义为
fd≡1-tanh((8rd)3)
(7)
式中:
(8)
其中:νt为湍流运动涡黏性系数;Ui,j为速度梯度张量;DDES的长度尺度为
(9)
由式(9)可以看出,当边界层延迟转捩函数fd=0时,DDES还原为S-A模型,当fd=1时,DDES模型与DES模型相同。由于fd在对数律层为1,到边界层边界迅速衰减为零,这样保证了在边界层内进行RANS计算时,同时起到了LES区与RANS区光滑过渡的作用。
2.3 网格生成方法
目前动网格技术较多采用基于变形与重构的非结构动态网格生成方法实现,但是非结构网格计算精度较低,同时网格重构又会带来新的插值误差。由于前置小翼展开过程外形变化较大,流场拓扑复杂,为了在保持原有网格拓扑结构不变的情况下,实现小翼展开过程的气动网格变化,避免出现网格扭曲及插值带来的误差问题,考虑采用结构化网格,利用基于弧长的超限插值(TFI)方法实现网格跟随变形边界的运动,较好地保证了内部网格质量,特别是边界层内网格质量。同时,采用文献[22-23]中的体积修正法解决几何守恒律问题,有效避免了网格变形诱导产生的非物理解。图4(a)给出了翼面伸出后的局部网格。
在网格生成过程中,首先根据小翼展开的区域及特点,采用分区对接方式划分初始网格,并预留出变形区域,如图4(b)虚线框所示。由于翼面展开的轨迹及速度已知,在不同时刻计算出翼面角点及棱线相对上一时刻的变形量,通过二维TFI方法得到翼面网格的变形量,再利用三维TFI方法得到与翼面相关的网格块内点扰动量,将扰动量与上一时刻网格相加得到本时刻变形后的网格,图4(c)给出了典型时刻变形后的网格。


图4 典型时刻结构动网格Fig.4 Moving structure grids at typical times
2.4 边界条件
1) 入流边界:来流为超声速,入流边界处给定来流的静压、静温及马赫数。
2) 出流边界:出口为超声速时,下游流场不影响上游流场,将所有参数数值外推。
3) 物面边界:壁面速度满足无滑移条件,壁面压力满足法向动量方程,壁面密度利用绝热壁条件和完全气体状态方程确定[22]。
2.5 数值模拟方法验证
根据研究外形及问题特点,采用尖拱形圆柱体模型以及Basic Finner模型分别验证建立的高精度RANS/LES混合数值模拟方法,验证模型及试验条件具体见文献[24-25]。图5和表2给出了尖拱形圆柱体模型的外形示意图与计算条件,其中φ为横截面子午角。图6给出了计算得到的尖拱形圆柱体模型中心线压力分布计算与试验对比情况,可以看出,计算与试验结果吻合较好。
数字化档案的文种形式、载体形式、表达形式都具有多样性,因此数字化档案信息具有多源异构的特点,要建立统一的档案信息关联模型,需要分别采用不同的特征提取方法对多种类型的档案进行特征提取,其中特征信息可能包括时间、人物、地点、类型、保管期限、著录机构等。有的特征信息可以通过著录项获取,有的特征信息需要使用模式识别等人工智能技术从档案内容中提取,这些特征信息都是档案的属性数据,不同的属性数据分属不同的特征视图,将提取到的特征按照不同的视图分别构建特征关联图,再使用数据融合技术融合多个视图下的特征关联图,最终得到档案信息关联模型。为了描述方便,对档案关联模型中的基本元素进行如下定义:
图7和表3分别给出了Basic Finner模型的外形示意图与计算条件,其中D为直径。图8给出了Basic Finner外形动态特性计算与试验对比情况,并与文献结果[26]进行了比对,可以看出,采用本文DES方法计算得到的结果与试验趋势相同,并优于文献[26]的结果。
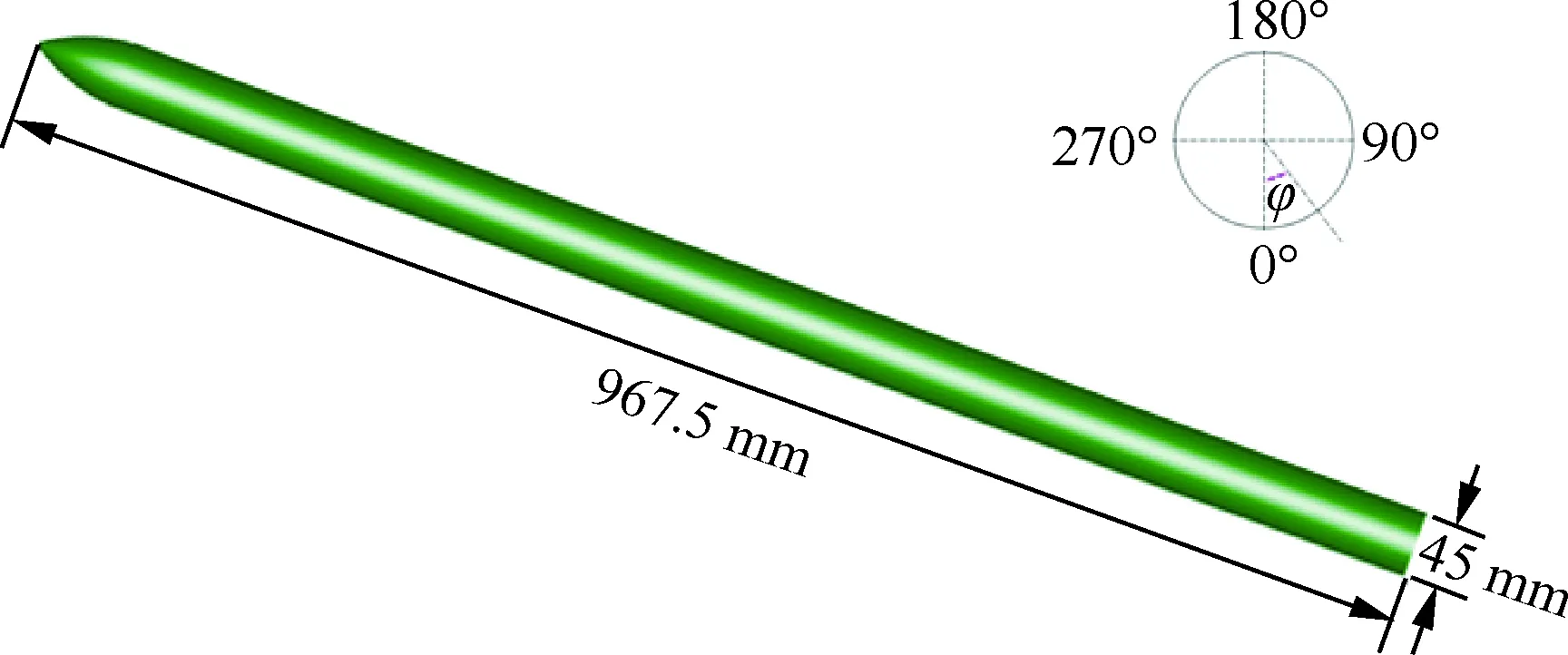
图5 尖拱形圆柱体模型Fig.5 Model for ogive-circular cylinder body
表2尖拱形圆柱体模型的计算条件
Table2Calculationconditionsofmodelforogive-circularcylinderbody

马赫数迎角/(°)静压/Pa静温/K雷诺数1.23041893.31248.44721.40×107

图6 中心线压力分布计算与试验对比Fig.6 Comparison of calculation and experiment results of pressure distribution at central lines (Ma∞=1.2,α=30°)

图7 Basic Finner 标模外形Fig.7 Model shape for Basic Finner

表3 Basic Finner模型计算条件Table 3 Calculation conditions of Basic Finner model
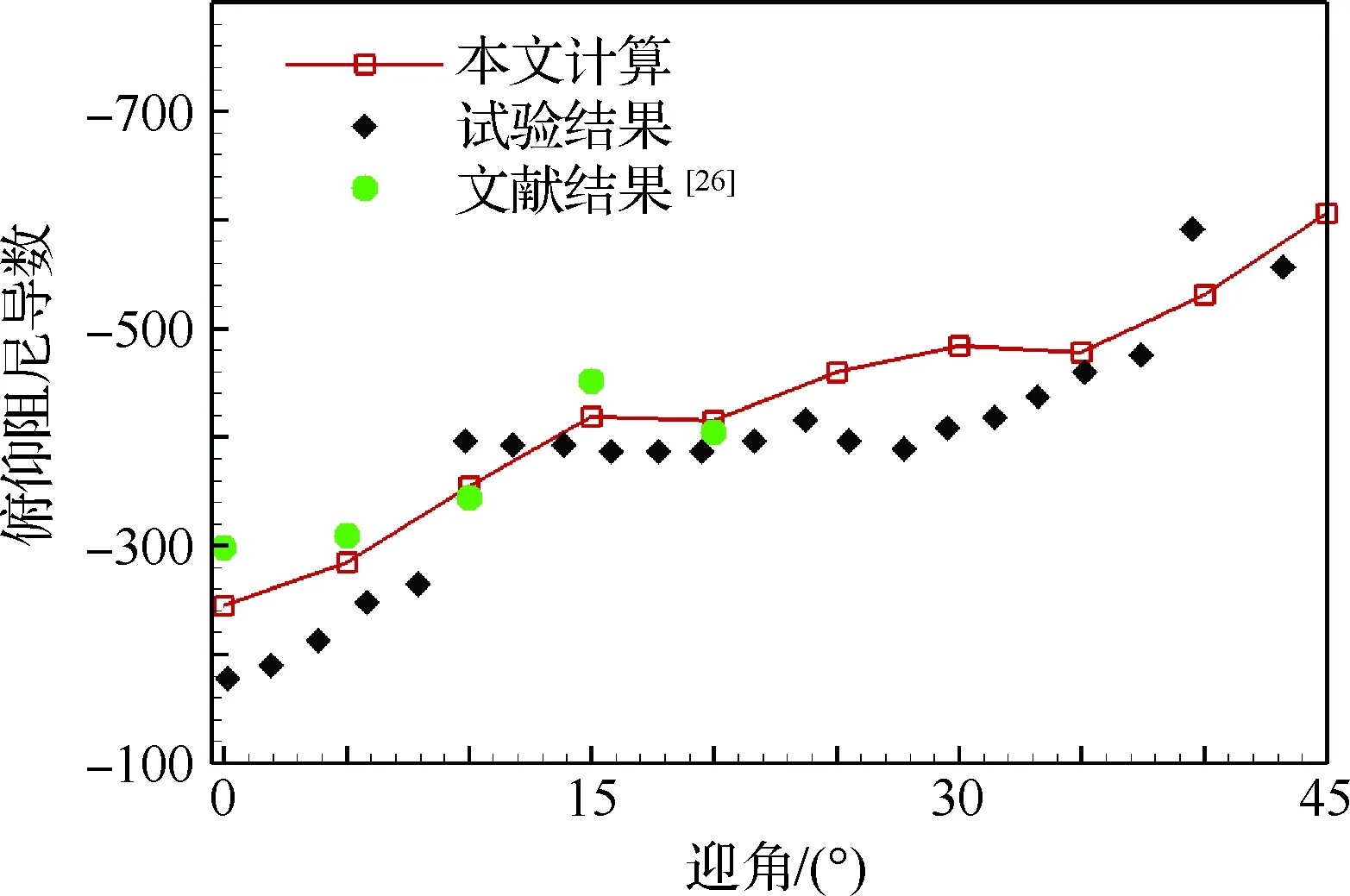
图8 Basic Finner外形俯仰阻尼导数计算与试验对比(Ma∞=1.96,Re=6.233×106)Fig.8 Comparison of calculation and experiment results of pitch damping derivatives of Basic Finner model (Ma∞=1.96,Re=6.233×106)
3 结果与分析
本文采用结构动网格技术以及非定常DES方法,就图1细长飞行器外形开展了前置小翼展开过程非定常数值仿真研究和分析。
3.1 小翼展开过程定常与非定常流场特性对比
图9给出了Ma∞=2.0、α=15°条件下4片前置小翼以相同角速度(660 (°)/s)同时展开过程中典型时刻相对初始状态的压力差(p-p初值)/p∞云图,图中前置小翼展开角度分别为φ=10°、20°、30°。可以看出,小翼展开过程中,翼面附近流场发生显著变化,翼后近区迎风面高压沿小翼后缘向侧面发展,背风面高压同时也向侧面加强和发展,最后背风面和迎风面的两片高压区连通,呈“X”形分布。同时可观察到,小翼展开对弹体中段和尾段也有较明显的干扰影响,在载荷计算时需要特别关注。

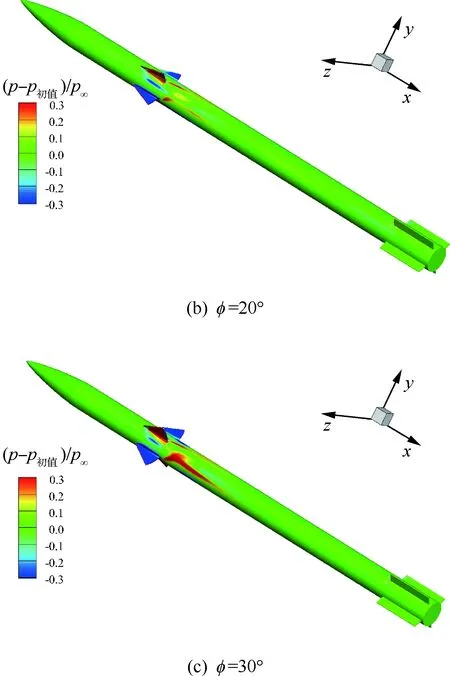
图9 小翼展开过程相对初始状态的表面压力差云图Fig.9 Contours of difference in surface pressure relative to the initial state during the spreading of wings (Φ=45°,Ma∞=2.0,α=15°)
为直观地分析小翼展开过程飞行器表面的非定常流场特性,图10给出了非定常与定常表面压力差(p非定常-p定常)/p∞云图以及翼面和尾舵侧面局部放大图。从图中可见,非定常效应主要集中在翼面及尾舵附近。一方面,随着翼面的展开,其附近非定常效应从背风面向迎风面发展,对上翼面产生的法向力和抬头力矩有所抵消;同时,翼后圆柱体上的高压区也从侧面向迎风面发展,产生附加的法向力和抬头力矩,两者互有消长。


图10 小翼展开过程非定常与定常表面压力差云图(Φ=45°,Ma∞=2.0,α=15°)Fig.10 Contours of difference in surface pressure of the unsteady and steady solutions during spreading of wings (Φ=45°,Ma∞=2.0,α=15°)
另一方面,非定常方法真实模拟了小翼对尾舵的洗流影响,尾舵区表现出明显的非定常效应。由尾舵附近局部放大图可见,背风面和迎风面云图结构类似,略有差别。主要特征是上下对称,在φ=20°时几乎完全对称,而φ=10°和φ=30°则有不同,上舵面的高压产生附加的法向力和低头力矩,而其根部圆柱体上的高压则使法向力减小并产生附加的抬头力矩。非定常效应的集中体现最终取决于小翼展开过程中以上各部分贡献。
为了进一步分析小翼展开过程非定常效应对空间流场的影响,图11给出了小翼附近(X=1 500 mm)、中距(X=2 400 mm)和远距(X=3 500 mm)的截面横向流。从图中可以看出,随着流场向下游发展,涡的结构尺度逐渐变大,涡核有远离物面的趋势,同时涡的形状从类圆形渐变成类椭圆形。还可看出,随着小翼的展开,涡的结构开始变得复杂,出现双涡结构,表明流场中出现了涡的分裂与合并。还可进一步看出,非定常与定常流场结构基本一致,在物面附近卷起典型的涡旋,但涡的尺度、涡核位置有所不同。仔细观察,可以发现在小翼附近和翼后中距处一致性较高,差异最明显的是翼后远距处,说明前置小翼在展开过程中与尾舵之间存在明显的远距干扰现象。
3.2 气动特性随小翼展开的变化
图12和图13分别给出了小翼展开过程中飞行器法向力系数和纵向压心系数的变化历程。可以看出,小翼展开过程中展开角度φ<10°时法向力系数变化较为平缓,展开角度φ≥10°时基本上呈线性增加趋势,纵向压心系数随小翼展开角度的增加而减小。对比图中定常和非定常结果,可以看出在展开角度φ=10°时,定常与非定常结果存在明显差异。表4详细给出了初始状态和小翼完全展开后的法向力和纵向压心系数对比情况,可以看出小翼完全展开后,法向力增加15.6%,提高了气动过载;压心前移4.1%,降低了飞行器的静稳定性,从而改善了飞行器的机动性能。


图11 小翼展开过程X=1 500, 2 400,3 500 mm截面横向流Fig.11 Crossflow at X=1 500, 2 400,3 500 mm cross-section during spreading of wings
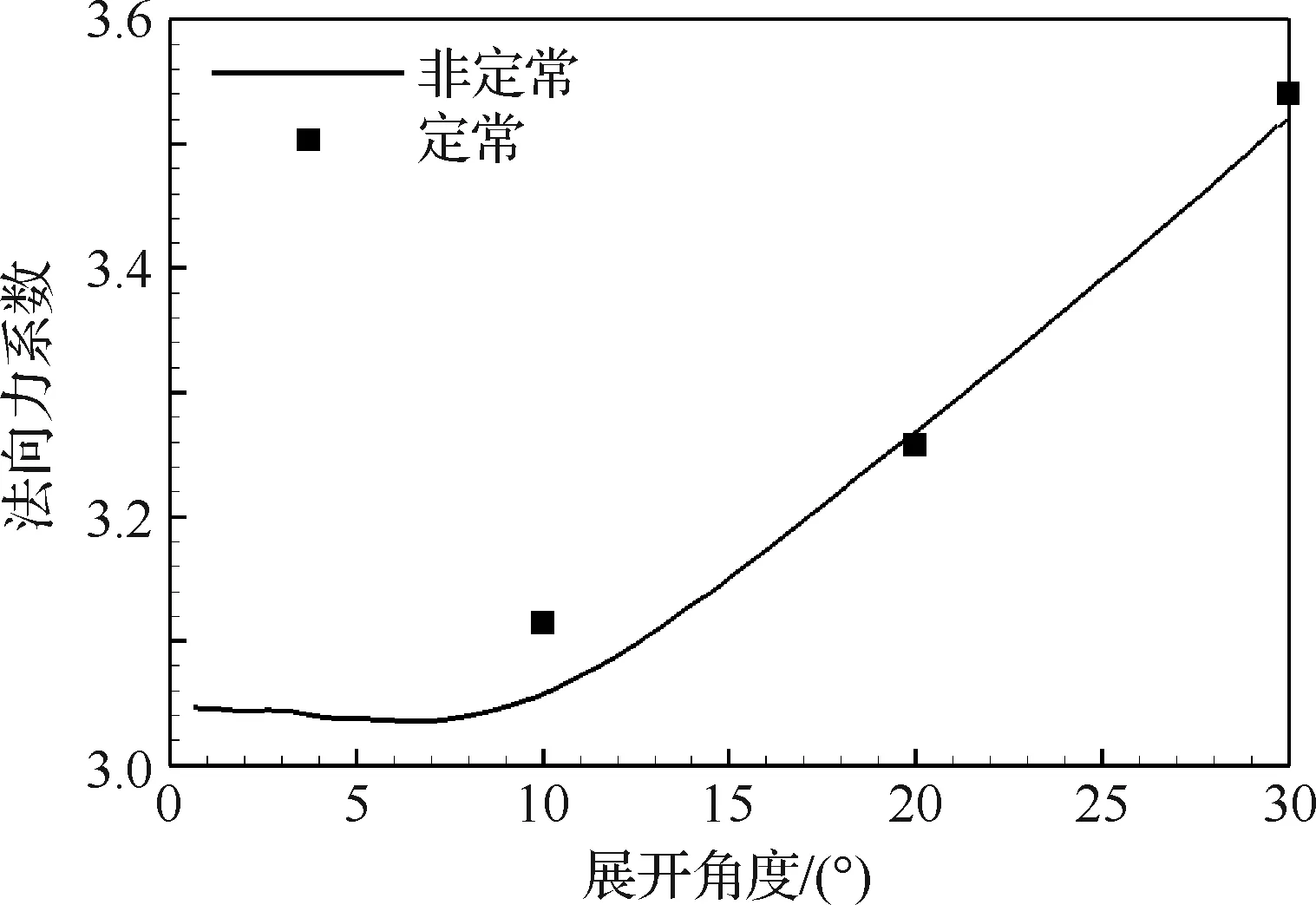
图12 小翼展开过程法向力系数的变化Fig.12 Variation in normal force coefficient during spreading of wings (Ma∞=2,α=15°,Φ=45°)

图13 小翼展开过程纵向压心系数的变化Fig.13 Variation in center of pressure coefficient during spreading of wings (Ma∞=2,α=15°,Φ=45°)
表4小翼展开前后法向力和纵向压心系数结果对比
Table4Comparisonofnormalforceandcenterofpressurecoefficientsbeforeandafterspreadingofwings

系数展开前展开后差量百分比法向力3.0463.5210.47515.6纵向压心0.523870.48250-0.041374.1
4 结 论
利用结构动网格技术和基于脱体涡(DES)的非定常数值模拟方法,研究了细长飞行器前置小翼展开过程的非定常效应。文中给出了小翼展开过程的详细动态流场特性,并分析研究了法向力、纵向压心系数随小翼展开过程的变化规律。
1) 采用的数值方法计算结果与试验吻合良好,方法具有较高的可信度与适用性。
2) 超声速、大迎角条件下前置小翼展开过程非定常效应显著。
3) 小翼展开过程对小翼附近区域以及尾舵区域产生了强烈的影响。
4) 小翼展开后压心前移,降低了飞行器的静稳定性,法向力系数增大,提高了气动过载,对飞行器机动性能都产生了有利影响。
参 考 文 献
[1] CHAMBERLAIN R, MCCLURE D, DANG A. CFD analysis of lateral jet interaction phenomena for the THAAD interceptor: AIAA-2000-0963[R]. Reston, VA: AIAA, 2000.
[2] DASH S M, PERRELL E R, ARUNAJATESAN S, et al. Lateral jet aerodynamic interaction simulations for dynamic pressure loads: AIAA-2000-2036[R]. Reston, VA: AIAA, 2000.
[3] EBRAHIMI H B. Numerical investigation of jet interaction in a supersonic freestream: AIAA-2005-4866[R]. Reston, VA: AIAA, 2005.
[4] 刘耀峰. CFD软件研发和战术导弹喷流/绕流复杂流动数值模拟[D]. 北京: 北京理工大学, 2005: 56-88.
LIU Y F. Development of CFD software and complex flows numerical simulation for interaction flow field between external flow and jet flow of tactical missiles[D]. Beijing: Beijing Institute of Technology, 2005: 56-88 (in Chinese).
[5] CUI J, AGARWAL R K. 3-D CFD validation of an axisymmetric jet in cross-flow: AIAA-2005-1112[R]. Reston, VA: AIAA, 2005.
[6] RAUSCH J R, ROBERTS B B. Reaction control system plume flow field interaction effects on the space shutter orbiter: AIAA-1974-1104[R]. Reston, VA: AIAA, 1974.
[7] YANG G, YAO Y F, FANG J, et al. Large-eddy simulation of shock-wave/turbulent boundary layer interaction with and without SparkJet control[J]. Chinese Journal of Aeronautics, 2016, 29(3): 617-629.
[8] SPALART P R, JOU W H, STRELETS M, et al. Comments on the feasibility of LES for wings, and on a hybrid RANS/LES approach[C]∥LIU C Q, LIU Z N. Advances in DNS/LES, 1st AFOSR International Conference on DNS/LES. Los Angles: Greyden Press, 1997: 137-147.
[9] STRELETS M. Detached eddy simulation of massively separated flows: AIAA-2001-0879[R]. Reston, VA: AIAA, 2001.
[10] 肖志祥, 符松. 用RANS/LES混合方法研究超音速底部流动[J].计算物理, 2009, 26(2): 221-230.
XIAO Z X, FU S. Study on supersonic base flow using RANS/LES methods[J]. Chinese Journal of Computational Physics, 2009, 26(2): 221-230 (in Chinese).
[11] SOSHI K, KOZO F. Computational study of a supersonic base flow using LES/RANS hybrid methodology: AIAA-2004-0068[R]. Reston, VA: AIAA, 2004.
[12] 赵伟文, 万德成. 用SST-DES和SST-URANS方法数值模拟亚临界雷诺数下三维圆柱绕流问题[J]. 水动力学研究与进展, 2016, 31(1): 1-8.
ZHAO W W, WAN D C. Numerical study of 3D flow past a circular cylinder at subcritical Reynolds number using SST-DES and SST-URANS[J]. Chinese Journal of Hydrodynamics, 2016, 31(1): 1-8 (in Chinese).
[13] 孙明波, 梁剑寒, 王振国. 超音速来流横向狭缝喷流标量输运的混合RANS/LES模拟[J]. 力学季刊, 2007, 28(3): 395-399.
SUN M B, LIANG J H, WANG Z G. Hybrid RANS/LES simulation for scalar transport of slot injection into a supersonic stream[J]. Chinese Quarterly of Mechanics, 2007, 28(3): 395-399 (in Chinese).
[14] WON S H, JEUNG I S, CHOI J Y. DES study of transverse jet injection into supersonic cross flows: AIAA-2006-1227[R]. Reston, VA: AIAA, 2006.
[15] SHIN J R, CHOI J Y. DES study of base and base-bleed flows with dynamic formulation of DES constant: AIAA-2011-0662[R]. Reston, VA: AIAA, 2011.
[16] 周铸, 黄江涛, 黄勇, 等. CFD技术在航空工程领域的应用、挑战与进展[J]. 航空学报, 2017, 38(3): 020891.
ZHOU Z, HUANG J T, HUANG Y, et al. CFD technology in aeronautic engineering field: Applications, challenges and development[J]. Acta Aeronautica et Astronautica Sinica, 2017, 38(3): 020891 (in Chinese).
[17] ROE P L. Approximate Riemann solvers, parameter vectors and different schemes[J]. Journal of Computational Physics, 1981, 43(2): 357-372.
[18] 唐海敏. 三维带操纵面机翼Euler方程非定常气动力计算[D]. 南京: 南京航空航天大学, 2003: 12-13.
TANG H M. Aerodynamic computation of 3-D unsteady Euler equations for wings with control surface[D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2003: 12-13 (in Chinese).
[19] JAMESON A. Time dependent calculations using multigrid, with applications to unsteady flows past airfoils and wings: AIAA-1991-1596[R]. Reston, VA: AIAA, 1991.
[20] YOON S, JAMESON A. Lower-upper symmetric-Gauss-Sediel method for the Euler and Navier-Stokers equations[J]. AIAA Journal, 1988, 26(9): 1025-1026.
[21] SPALART P R, ALLMARAS S R. A one-equation turbulence model for aerodynamic flows: AIAA-1992-0439[R]. Reston, VA: AIAA, 1992.
[22] 王巍. 有相对运动的多体分离过程非定常数值算法研究及试验验证[D]. 长沙: 国防科学技术大学, 2008: 29-31.
WANG W. Numerical simulation technique research and experiment verification for unsteady multi-body flowfield involving relative movement[D]. Changsha: National University of Defense Technology, 2008: 29-31 (in Chinese).
[23] 刘君, 刘瑜, 陈泽栋. 非结构变形网格和离散几何守恒律[J]. 航空学报, 2016, 37(8): 2395-2407.
LIU J, LIU Y, CHEN Z D. Unstructured deforming mesh and discrete geometric conservation law[J]. Acta Aeronautica et Astronautica Sinica, 2016, 37(8): 2395-2407 (in Chinese).
[24] BARCHE J. Experimental data base for computer program assessment[R]. London: Technical Editing and Reproduction Ltd, 1979.
[25] USELTON B L, USELTON J C. Test mechanism for measuring pitch damping derivatives of missile configurations at high angles of attack: AEDC-TR-75-43[R]. Tennessee: Arnold Engineering Development Center, 1975.
[26] SCOTT M M. A reduced-frequency approach for calculating dynamic derivatives: AIAA-2005-0840[R]. Reston,VA: AIAA, 2005.

