后缘小翼对旋翼气动特性的控制机理及参数分析

马奕扬，招启军

南京航空航天大学 直升机旋翼动力学国家级重点实验室，南京 210016

在直升机前飞速度和旋翼旋转速度的综合作用下，直升机桨叶在前行侧(跨声速区)和后行侧(低速区)分别面临着不同的来流条件。为了避免由此带来的较大滚转力矩，后行桨叶总是处在迎角较大的状态下，而前行桨叶的迎角则较小。迎角的这一周期性变化会引起复杂的非定常动态失速现象，动态失速会导致阻力系数、力矩系数的突增以及较大的俯仰力矩和振动载荷的产生[1]，从而严重制约着直升机气动性能和飞行速度的提高。

近年来，寻找能在不同飞行条件下提高旋翼性能的控制技术逐渐成为热点。传统的被动设计技术，包括桨叶几何外形优化、固定前缘条等，很难同时满足对前行桨叶压缩性以及后行桨叶失速特性的不同要求。因此，主动流动控制技术逐渐成为目前直升机旋翼技术的一个重要领域，例如动态前缘、合成射流技术[2]以及后缘小翼(TEF)控制等。其中，主动控制后缘小翼技术由于其结构紧凑、重量轻、需用功率小、带宽高的特点[3]，根据不同的需求，每片桨叶后缘处可以设计一片或多片后缘小翼，从而增加控制的自由度，通过控制小翼合理的偏转，产生附加的气动力/力矩，影响旋翼的流场与气动弹性响应，实现多样化的控制目标，例如抑制振动及噪声、提高旋翼性能以及增加旋翼的动力学稳定性。相比于其他旋翼主动控制方法，后缘小翼主动控制系统可以将其完全镶嵌于桨叶内部，不会增加额外的气动阻力。此外，TEF与旋翼基础操纵系统相互独立，TEF系统发生故障时不至于危及直升机的飞行控制安全。

在试验研究方面，Hassan等[4]开展了带后缘小翼的HH-06和HH-10两个翼型的风洞试验，研究结果表明，小翼偏置的尺寸对翼型俯仰力矩和阻力影响显著。2000年，Boeing公司、NASA和美国陆军(Army)等机构组成的团队进行了SMART (Smart Material Actuated Rotor Technology)旋翼试验和全尺寸的后缘小翼智能旋翼风洞试验，验证了主动控制后缘小翼在降低旋翼振动噪声，提高气动性能等方面的能力。欧洲直升机公司(Eurocopter)的ADASYS旋翼项目于2005年9月8日在德国实现了后缘小翼智能旋翼直升机的首次试飞，标志着后缘小翼旋翼技术研究达到了一个新高度[5-6]。2009—2011年，Eurocopter进行了名为Blue Pulse[7]的新一轮带后缘小翼智能旋翼的直升机飞行试验，此次试验的验证机以EC145直升机为原型。与ADASYS验证机相比，可以选择使用单片小翼或者多片小翼，在抑制振动和噪声的同时，提高直升机“地面共振”、空中共振的稳定性。

早期的计算流体力学(CFD)方法的计算精度和计算机能力有限，CFD方法不足以取代风洞试验或飞行试验。随着计算方法的改进和计算机运行速度的提升，CFD方法逐渐被用于带后缘小翼翼型及旋翼的研究中。Shen[8]、Straub[9]和Mishra[10]等通过数值模拟研究了后缘小翼对旋翼振动水平和气动特性的影响，发现后缘小翼在高阶信号的输入下，能够降低旋翼的振动水平，同时提升旋翼的气动性能。Mishra等[11]通过CSD/CFD耦合的数值模拟方法，验证了后缘小翼在缓解旋翼动态失速上的潜力。Jain和Ravichandran等[12-13]研究得出通过适当偏转后缘小翼，可以调节桨叶剖面的气动特性，对较小的载荷进行再分配更有利于提升大速度情况下旋翼的气动特性，但尚未开展系统性的参数影响分析。

国内方面，刘洋和向锦武[14]利用CFD方法及动网格技术对带后缘小翼的二维翼型动态失速特性进行了仿真，证实了后缘小翼可以对动态失速起到一定的延缓作用，但尚未拓展到三维旋翼应用上。马奕扬等[15]针对后缘小翼的典型运动参数对旋翼翼型动态失速特性的控制进行了研究，但尚未开展后缘小翼对三维旋翼气动特性的控制机理和参数分析。

尽管先期的试验和数值研究已表明后缘小翼在提升旋翼气动性能和控制动态失速方面有很大的应用潜力，但目前关于后缘小翼提升旋翼气动特性的系统性参数分析研究依然缺乏。一方面,建立一套高精度的CFD方法存在挑战，具体原因是：首先，后缘小翼空间位置的不断变化对贴体网格生成提出了很高的要求。其次，由于桨叶存在多种运动耦合，变形网格方法会出现网格的较大畸变，需要发展可靠的运动嵌套网格方法。此外，面对直升机在前飞流场中存在的激波/附面层干扰和动态失速现象，需要采用高精度的CFD方法来进行有效模拟。另一方面，后缘小翼的控制参数较多(运动规律、安装位置、大小尺寸等)，不同控制参数对旋翼气动特性的影响机理目前仍然不清楚，因此开展系统性的后缘小翼参数影响分析是必要的。

本文首先基于“扰动衍射”挖洞方法和最小距离法建立了一套围绕带有后缘小翼旋翼的运动嵌套网格方法；为了提高求解精度和计算效率，将Roe-MUSCL (Roe-Monotone Upwind-centered Scheme for Conservation Laws)格式，隐式LU-SGS (Lower-Upper Symmetric Gauss-Seidel)方法相结合，湍流模型采用二方程的k-ω剪切应力输运(SST)模型。然后，通过对AH-1G旋翼和带后缘小翼的SMART旋翼作为算例，验证CFD方法的有效性。最后，着重开展对带后缘小翼旋翼的系统性参数分析，在操纵量不变的情况下分别研究偏转幅值、偏转频率、后缘小翼的安装位置及宽度等参数对旋翼气动特性的控制机理，获得典型参数的影响特性。进一步研究配平状态下后缘小翼对旋翼气动特性的影响，验证后缘小翼在降低旋翼的阻力系数、扭矩系数及提升升阻比上的潜力。

1 网格方法

1.1 翼型网格点重构

在模拟后缘小翼控制旋翼气动特性的过程中，后缘小翼的运动规律为

δ=δ0+δmsin(2k*kt-φ0)

(1)

式中：δ为翼型后缘小翼瞬时偏转角,当δ为正数时，表示后缘小翼向下偏转；δ0和δm分别为基准偏转角和偏转幅值；k为翼型振荡的减缩频率，k*为相对于k的运动频率；φ0为后缘小翼运动规律与周期变距之间的相位差。

在对网格修正之前，采用B样条插值法对后缘小翼附近的网格点进行重构，以避免小翼上下表面附近的网格点分布过于集中或稀疏对后续网格生成质量产生不利影响。图1给出了后缘小翼及网格点重构的示意图，从图中可以分别看出后缘小翼的偏转点、振荡中心、后缘小翼的偏转角和翼型的迎角，同时给出了初始翼型和带有后缘小翼翼型的网格点分布，c为翼型弦长。

图1 翼型振荡中心和后缘小翼示意图Fig.1 Sketch of oscillatory center of airfoil and TEF

1.2 运动嵌套网格方法

考虑到旋翼在旋转过程中的周期变距以及后缘小翼的周期性偏转运动，本文发展了一套适用于带有后缘小翼的旋翼非定常气动特性模拟的运动嵌套网格方法，并以此研究后缘小翼对旋翼气动特性的控制效果。

首先，通过求解泊松方程来获得二维翼型各剖面的网格(包括带有后缘小翼的二维翼型)，然后对各剖面网格进行展向插值，得到整个桨叶的网格。为了更好地模拟后缘小翼对旋翼气动特性的控制效果，展向上的后缘小翼位置需要做加密处理。桨尖部分采用绕翼型中弧线翻折策略，生成围绕桨叶的三维C-O型结构网格。图2给出了带有后缘小翼的旋翼桨叶贴体网格示意图。

考虑到前飞情况，背景网格选取长方体的笛卡儿网格。并且，为了更精确地模拟后缘小翼对旋翼气动特性的控制效果，对旋翼桨叶网格附近的背景网格进行了加密。

此外，本文采用了改进的“扰动衍射”挖洞方法[16]来处理桨叶网格与背景网格之间的嵌套关系。为实现对背景网格洞边界单元的贡献单元进行快速搜寻，本文将二维最小距离法[16]推广到三维情况，较大程度上提高了流场计算效率。图3给出了本文建立的运动嵌套网格系统示意图。

图2 带有后缘小翼的旋翼桨叶贴体网格示意图Fig.2 Sketch of body-fitted grids around blade of rotor with TEF

图3 运动嵌套网格系统示意图Fig.3 Sketch of moving-embedded grid system

2 数值方法

2.1 非定常流场求解方法

综合考虑带有后缘小翼的前飞旋翼非定常流场的复杂性，本文采用非定常雷诺平均Navier-Stokes(URANS)方程模拟整个旋翼流场，即

(2)

式中：W为守恒变量；Fc和Fv分别为修正对流通量和黏性通量；τ和t分别为虚拟时间和物理时间；Ω为单元体的体积；S为网格单元的边界。

基于控制体表面的逆变速度Vt和初始的对流通量Fc,0，修正后的对流通量Fc为

Fc=Fc,0-VtW

(3)

本文采用格心有限体积法在空间方向上进行离散，对流通量采用Roe[17]和MUSCL格式[18]相结合的方法进行计算，黏性通量采用Jameson二阶中心差分方法求解。湍流黏性系数计算采用二方程k-ωSST湍流模型[19]。

为模拟带有后缘小翼的旋翼流场非定常特性，采用双时间方法进行时间推进。在进行虚拟时间推进时，考虑流场的收敛性，显式方法的时间步长要求取得较小，这降低了数值模拟的效率。针对这一问题，本文虚拟时间步采用隐式LU-SGS格式[20]的方法进行推进，从而有效加大时间步长，提高计算效率。此外，由于网格的位置、形状均随时间不断变化，为了避免由于网格运动引入的额外误差，几何守恒律必须得到严格满足。

2.2 数值方法验证

本文针对前飞状态AH-1G旋翼气动特性进行了模拟。AH-1G旋翼含有两片矩形桨叶，展弦比为9.22。桨叶剖面翼型为OLS翼型，从桨根到桨尖的线性扭转为-10°。计算状态为桨尖马赫数Matip=0.65, 前进比μ=0.19, 雷诺数Re=9.73×106，旋翼操纵量的配平量为

式中：θ为周期变距；β为周期挥舞角；ψ为方位角。

图4分别给出了桨叶不同剖面处的法向力系数Cn分布情况，r为桨叶展向位置，R为旋翼桨叶半径。由图可以看出，本文计算结果与试验值[21]吻合良好，表明本文发展的方法能够有效地模拟旋翼在前飞状态下的气动特性。

图4 AH-1G旋翼法向力系数的计算值与试验值对比Fig.4 Comparison of calculation results and experimental data of normal forces coefficients of AH-1G rotor

SMART旋翼试验是目前一个成功的带后缘小翼的全尺寸旋翼风洞试验，文献[22]中使用两种方法对该旋翼进行了分析，方法1为Free wake/UMARC耦合计算方法，方法2为CFD/UMARC耦合计算方法，计算文献[22]的Case 2状态。选取两个典型剖面(小翼中部0.828R和小翼外部0.92R)，分别计算考虑到小翼偏转对这些剖面的等效法向力的影响，验证本文方法计算带小翼旋翼气动载荷的能力。从图5可以看出，3种计算方法得到的等效法向力系数CnMa2结果接近，证明本文模型对带后缘小翼的旋翼气动载荷计算结果是可靠的，可用于后续带后缘小翼旋翼气动载荷的分析。

图5 带后缘小翼桨叶不同剖面的等效法向力系数比较Fig.5 Comparison of equivalent normal forces at different blade sections of rotor with TEF

3 气动特性控制机理及参数分析

为了获得不同控制参数对旋翼气动特性的影响规律，避免因为旋翼总距和周期变距操纵引起的旋翼气动力变化，本文首先在操纵量不变的情况下，分别研究了后缘小翼偏转幅值、偏转频率、安装位置以及宽度等参数对前飞状态旋翼气动特性的影响。所研究的旋翼由两片矩形桨叶构成，桨叶剖面翼型为VR-12翼型，展弦比为15，无负扭转，在0.5R～0.8R桨叶段含有25%c的后缘小翼。

3.1 偏转幅值

首先，针对后缘小翼的偏转幅值δm对旋翼非定常气动特性改善效果的影响开展了数值研究。计算状态桨尖马赫数Matip=0.62，旋翼前进比μ=0.2，旋翼桨叶旋转一周的变距规律为：θ=10°-7°sinψ+4°cosψ。后缘小翼的偏转幅值分别设置为5°和10°，参考带有后缘小翼的翼型在振荡状态下的分析结果[15]，将后缘小翼的无量纲偏转频率固定为k*=1.0。

图6为不同后缘小翼控制下旋翼气动特性的对比。随着后缘小翼偏转幅值δm的增大，旋翼拉力系数CT显著增大，旋翼阻力系数(逆旋翼前进方向所受合力，CD)会有一定的减少；旋翼扭矩系数CQ受后缘小翼偏转幅值的影响较大，当桨叶在后行侧时，扭矩系数会随δm的增大而减小，这非常有利于缓解旋翼动态失速引起的大扭矩响应，有助于提高直升机的前飞速度。

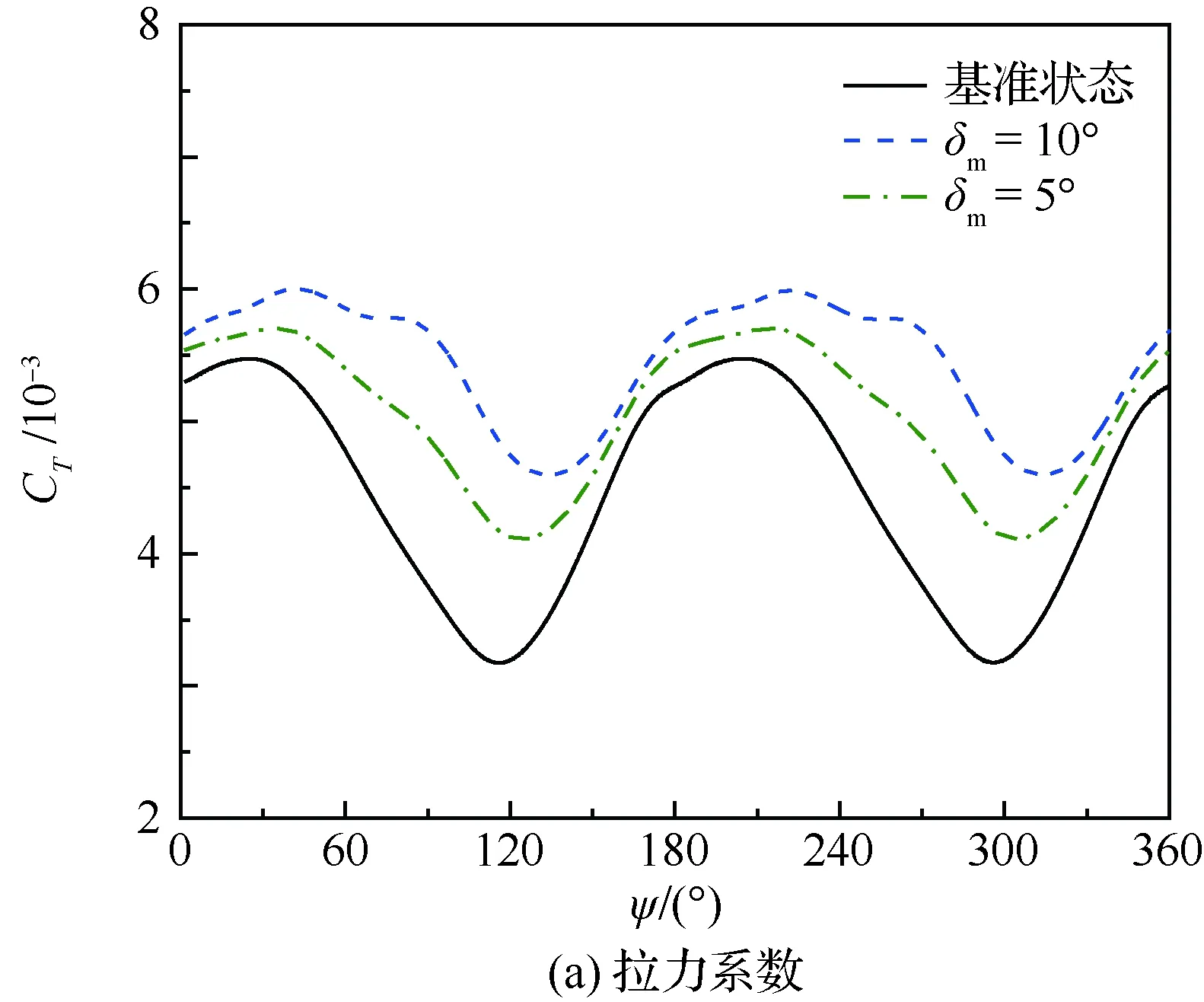
图6 TEF偏转幅值对旋翼气动特性的影响Fig.6 Influence of TEF deflection amplitude on rotor aerodynamic characteristics

3.2 无量纲偏转频率

从二维旋翼翼型动态失速的后缘小翼控制分析[15]中可以看出，当后缘小翼的无量纲偏转频率k*=1.0时，后缘小翼对翼型动态失速控制的效果最好，在三维情况下控制效果是否一致需要进一步研究。为此，本文开展了后缘小翼的偏转频率对旋翼气动特性控制的影响。在进行数值计算时，旋翼运动参数与3.1节相同，后缘小翼的偏转幅值设置为δm=10°。

图7分别给出了不同无量纲偏转频率情况下后缘小翼对旋翼气动特性的控制效果对比。可以看出，后缘小翼频率的增大会引起旋翼气动特性参数的振荡。

图7 TEF偏转频率对旋翼气动特性的影响Fig.7 Influence of TEF deflection frequency on rotor aerodynamic characteristics

表1进一步给出了不同TEF偏转频率控制下的旋翼平均气动力系数,表中下标aver代表参数平均值。从表中可以看出，当k*=1.0时，旋翼的平均拉力提升最为明显。对于旋翼产生的阻力系数，k*的增大使得阻力系数的振荡频率增大，但对旋翼平均阻力系数影响不明显。当k*>1.0时，随着k*的增大，旋翼产生的扭矩系数振荡明显，且平均扭矩系数均大于k*=1.0时的控制状态。

表1不同TEF偏转频率控制下的平均气动力系数

Table1AverageaerodynamiccoefficientsofTEFcontrolwithdifferentdeflectionfrequencies

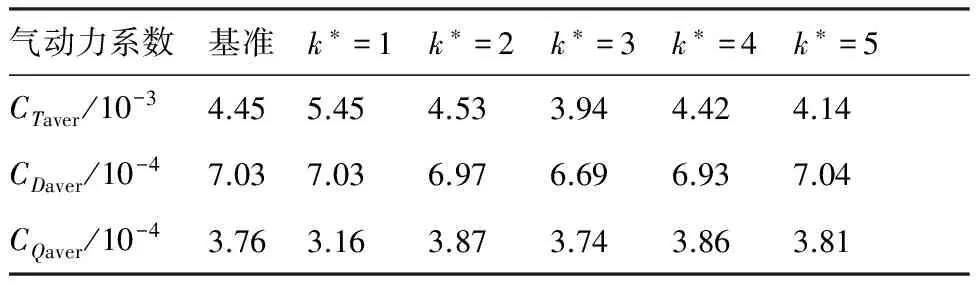
气动力系数基准k∗=1k∗=2k∗=3k∗=4k∗=5CTaver/10-34．455．454．533．944．424．14CDaver/10-47．037．036．976．696．937．04CQaver/10-43．763．163．873．743．863．81

3.3 小翼位置

进一步开展后缘小翼的安装位置对旋翼非定常气动特性的影响分析。旋翼运动参数与3.1节相同，后缘小翼的偏转幅值和无量纲偏转频率分别设置为δm=10°和k*=1.0，后缘小翼的宽度设置为0.3R。

图8分别给出了不同展向位置的后缘小翼对旋翼气动特性的控制效果对比。可以看出，后缘小翼在桨叶不同展向位置对旋翼拉力都有较好的提升效果；随着后缘小翼位置更接近桨尖，旋翼阻力系数和扭矩系数都显著降低。分析原因可能是后缘小翼的安装位置越靠近桨尖，后缘小翼所处的位置相对法向来流速度越大，抑制分离效果越明显，从而有利于降低旋翼阻力和扭矩。

3.4 小翼宽度

以后缘小翼的宽度作为研究对象，进一步开展后缘小翼的宽度对旋翼非定常气动特性的影响分析。旋翼运动参数与3.3节相同，后缘小翼的偏转幅值和无量纲偏转频率分别设置为δm=10°和k*=1.0，后缘小翼安装在展向0.65R处，宽度分别设置为0.1R、0.2R和0.3R。

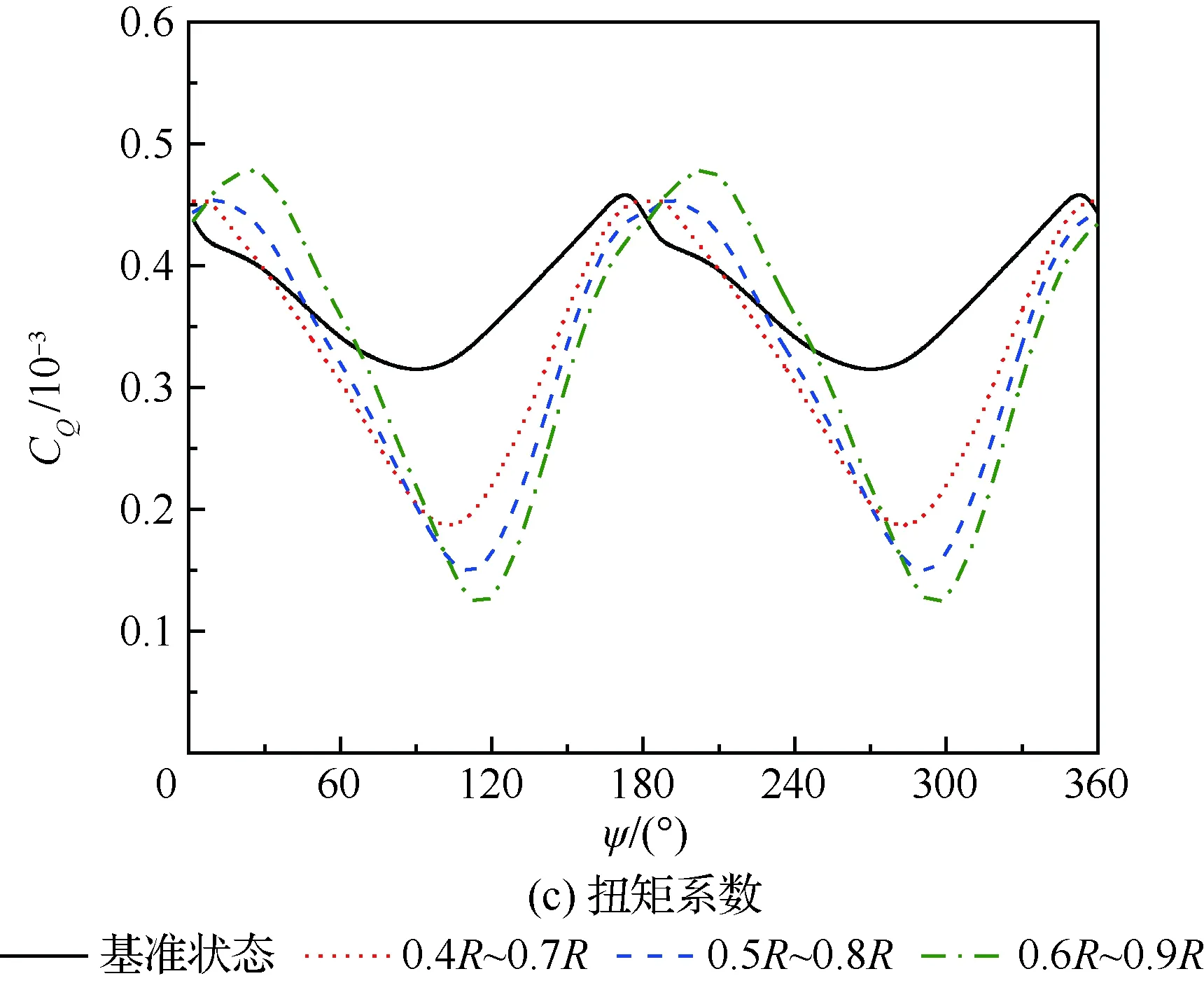
图8 TEF安装位置对旋翼气动特性的影响Fig.8 Influence of TEF installation position on rotor aerodynamic characteristics

图9分别给出了安装不同宽度的后缘小翼对旋翼气动特性的控制效果对比。从图中可以看出，随着后缘小翼宽度的增加，旋翼拉力系数逐渐增加；旋翼阻力系数随着后缘小翼宽度的增加略有降低；旋翼的扭矩系数会显著降低，因为随着后缘小翼宽度的增加，后缘小翼的影响区域越大。

图9 TEF宽度对旋翼气动特性的影响Fig.9 Influence of TEF width on rotor aerodynamic characteristics

4 有/无后缘小翼在相同拉力系数下的对比

为了进一步验证后缘小翼对旋翼气动特性的改善作用，本文在拉力系数配平的状态下，进行了有/无后缘小翼的旋翼前飞状态气动特性的对比。

4.1 不同方位角时的旋翼气动特性

首先，通过上述不同参数的影响研究表明，后缘小翼的无量纲频率k*=1.0时有较好的控制效果，为此后缘小翼的运动规律选择了δ=10°sin(2k*kt)，后缘小翼安装在距离桨毂中心0.5R～0.8R处，宽度为0.3R。

图10给出了有/无后缘小翼的旋翼在拉力系数配平状态下气动特性的对比。可以看出，当平均旋翼拉力系数相同(CTaver=4.5×10-3)时，后缘小翼可以有效地降低旋翼的阻力系数和扭矩系数。因此，旋翼的瞬时升阻比有显著提高。这里升阻比L/D的定义为

(4)

根据式(4)定义的升阻比，在旋翼拉力系数相同的条件下，没有安装后缘小翼的旋翼平均升阻比是1.72，装有后缘小翼的旋翼的平均升阻比是1.97，提高了14%，由此可见，后缘小翼提高了旋翼在前飞状态下的升阻比。

图11进一步给出了有/无后缘小翼的旋翼在拉力配平状态下平均拉力系数、阻力系数和扭矩系数的对比。从图中可以看出，在本文的计算状态下，通过后缘小翼控制可以有效地降低旋翼的阻力系数和扭矩系数，平均阻力系数和平均扭矩系数分别降低了17%和29%。

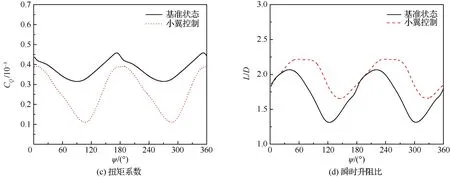
图10 有/无后缘小翼的旋翼在相同拉力下的气动特性Fig.10 Aerodynamic characteristics of rotor with/without TEF under the same tension state

图11 有/无后缘小翼的旋翼在相同拉力下的平均气动特性对比Fig.11 Comparisons of average aerodynamic characteristics of rotor with/without TEF under the same tension state

4.2 桨叶不同剖面的等效法向力

图12给出了在不同后缘小翼控制下桨叶不同剖面的等效法向力(CnMa2)分布情况。可以看出，具有后缘小翼的桨叶剖面，如图12(a)～图12(c)所示，法向力有显著变化：在后行桨叶一侧，后缘小翼控制下桨叶剖面法向力比基准状态有所降低；在旋翼前行侧，剖面法向力相对于基准状态有明显的增大。在靠近桨尖的桨叶剖面(无后缘小翼，如图12(d)和图12(e)所示)，尽管后缘小翼对剖面法向力的影响明显减弱，但是由于在0.5R～0.8R桨叶段后缘小翼对桨叶表面三维流动的控制作用，0.85R和0.95R剖面的法向力相对于基准状态仍有一定的变化。

4.3 桨叶不同展向位置压力系数分布

为了进一步分析4.2节桨叶不同剖面的等效法向力的变化规律，图13给出了桨叶不同展向位置的压力系数Cp分布。可以看出，具有后缘小翼的桨叶剖面段(0.5R～0.8R)翼型上下表面的压力系数有显著变化：剖面翼型的上下表面压强差显著增大，如图13(a)和图13(b)所示。在没有后缘小翼的剖面处(0.85R)，由于后缘小翼对桨叶表面三维流动的控制作用，剖面翼型的上下表面的压强差仍然有一定的增大。当剖面展向位置远离后缘小翼段时，后缘小翼对剖面翼型上下表面压强差的影响明显减弱，如图13(c)和图13(d)所示。

图12 有/无后缘小翼桨叶不同展向位置剖面等效法向力系数对比Fig.12 Comparison of equivalent normal force coefficients at different blade cross-sections with/without TEF

图13 不同桨叶展向位置的压力系数分布Fig.13 Pressure coefficients distribution at different blade cross-sections

4.4 桨叶不同方位角压力系数分布

图14分别给出了桨叶在不同方位角处的压力系数分布。可以看出，具有后缘小翼的桨叶剖面压力系数分布有显著变化：在旋翼前行侧，后缘小翼控制下桨叶剖面上下表面压强差相对于基准状态有明显的增大。原因在于，按后缘小翼当前的运动规律，在旋翼前行侧，后缘小翼向下偏转，翼型的弯度有显著的增加；在后行侧，后缘小翼向上偏转，拉力会有明显的降低，但阻力也会有明显的下降。当桨叶在方位角为180°和360°时，按后缘小翼当前的运动规律，此时后缘小翼并没有发生偏转，但是因为处在旋翼拉力系数一定的情况下，总距有所降低(降低了1.85°)，导致该方位角下的剖面上下表面压强差有所降低。

图14 不同方位角处的压力系数分布Fig.14 Pressure coefficients distribution at different azimuthals

5 结 论

1) 后缘小翼可以充分发挥旋翼在前行侧的升力，同时降低动态失速过程中旋翼的阻力和扭矩系数，从而兼顾桨叶在前行侧和后行侧时的不同性能需求。

2) 后缘小翼运动频率的增大会引起旋翼气动特性参数的振荡。当频率增大时，后缘小翼对旋翼非定常气动特性的提升效果减弱。

3) 对于阻力系数和扭矩系数，随着后缘小翼位置更接近桨尖，桨盘阻力系数和扭矩系数均有显著降低。

4) 随着后缘小翼宽度的增加，旋翼拉力系数逐渐增加，旋翼的扭矩系数会显著降低，而阻力系数变化不大。

5) 配平状态下后缘小翼可以有效降低旋翼阻力系数和扭矩系数，分别达到17%和29%。这有利于缓解旋翼动态失速引起的大扭矩响应，进一步提高直升机的前飞速度。

参 考 文 献

[1] YU Y H, LEE S, MCALISTER K W, et al. Dynamic stall control for advanced rotorcraft application[J]. AIAA Journal, 1995, 33(2): 289-295.

[2] ZHAO G Q, ZHAO Q J. Experimental investigations for parametric effects of dual synthetic jets on delaying stall of a thick airfoil[J]. Chinese Journal of Aeronautics, 2016, 29(2): 346-357.

[3] VISWAMURTHY S R, GANGULI R. Effect of piezoelectric hysteresis on helicopter vibration control using trailing-edge flaps[J]. Journal of Guidance, Control, and Dynamics, 2006, 29(5): 1201-1209.

[4] HASSAN A, STRAUB F, NOONAN K. Experimental/numerical evaluation of integral trailing edge flaps for helicopter rotor applications[J]. Journal of the American Helicopter Society, 2005, 50(1): 3-17.

[5] DIETERICH O, ENENKL B, ROTH D. Trailing edge flaps for active rotor control aeroelastic characteristics of the ADASYS rotor system[C]∥American Helicopter Society 62nd Annual Forum Proceedings. Alexandria, VA: The AHS International, Inc., 2006.

[6] ROTH D, ENEKL B, DIETERICH O. Active rotor control by flaps for vibration reduction-full scale demonstrator and first flight test results[C]∥Proceedings of 32nd European Rotorcraft Forum, 2006.

[7] RABOURDIN A, MAURICH J, DIETERICH O, et al. Blue Pulse active rotor control at Airbus Helicopters-New EC145 demonstrator and flight test results[C]∥American Helicopter Society 70th Annual Forum Proceedings. Alexandria, VA: The AHS International, Inc., 2009.

[8] SHEN J, CHOPRA I. Aeroelastic stability of trailing-edge flap helicopter rotors[J]. Journal of the American Helicopter Society, 2003, 48(1): 236-243.

[9] STRAUB F K, CHARLES B D. Aeroelastic analysis of rotors with trailing edge flaps using comprehensive codes[C]∥55th Annual Forum of the American Helicopter Society International. Alexandria, VA: The AHS International, Inc., 1999.

[10] MISHRA A, SITARAMAN J, BAEDER J, et al. Computational investigation of trailing edge flap for control of vibration[C]∥AIAA Applied Aerodynamics Conference. Reston, VA: AIAA, 2007: 1-12.

[11] MISHRA A, ANANTHAN S, BAEDER J. Coupled CFD/CSD prediction of the effects of trailing edge flaps on rotorcraft dynamic stall alleviation[C]∥AIAA Aerospace Sciences Meeting Including the New Horizons Forum and Aerospace Exposition. Reston, VA: AIAA, 2013: 423-429.

[12] JAIN R, YEO H, CHOPRA I. Computational fluid dynamics-computational structural dynamics analysis of active control of helicopter rotor for performance improvement[J]. Journal of the American Helicopter Society, 2010, 55: 42004.

[13] RAVICHANDRAN K, FALLS J, ANANTHAN S, et al. Active rotor controls for vibration reduction and performance enhancement[C]∥Proceedings of the AHS Specialists’ Conference on Aeromechanics. Alexandria, VA: The AHS International, Inc., 2010.

[14] 刘洋, 向锦武. 后缘襟翼对直升机旋翼翼型动态失速特性的影响[J]. 航空学报, 2013, 34(5): 1028-1035.

LIU Y, XIANG J W. Effect of the trailing edge flap on dynamic stall performance of helicopter rotor airfoil[J]. Acta Aeronautica et Astronautica Sinica, 2013, 34(5): 1028-1035 (in Chinese).

[15] 马奕扬, 招启军, 赵国庆. 基于后缘小翼的旋翼翼型动态失速控制分析[J]. 航空学报, 2017, 38(3): 120312.

MA Y Y, ZHAO Q J, ZHAO G Q. Dynamic stall control of rotor airfoil via trailing-edge flap[J]. Acta Aeronautica et Astronautica Sinica, 2017, 38(3): 120312 (in Chinese).

[16] 赵国庆, 招启军, 王清. 旋翼翼型非定常动态失速特性的CFD 模拟及参数分析[J]. 空气动力学学报, 2015, 33(1): 72-81.

ZHAO G Q, ZHAO Q J, WANG Q. Simulations and parametric analyses on unsteady dynamic stall characteristics of rotor airfoil based on CFD method[J]. Acta Aerodynamica Sinica, 2015, 33(1): 72-81 (in Chinese).

[17] ROE P L. Approximate Riemann solvers, parameter vectors and difference schemes[J]. Journal of Computational Physics, 1981, 43(2): 357-372.

[18] VAN LEER B. Towards the ultimate conservative difference scheme. V. A second-order sequel to Godunov’s method[J]. Journal of Computational Physics, 1997, 32(1): 101-136.

[19] MENTER F R. Two-equation eddy-viscosity turbulence models for engineering applications[J]. AIAA Journal, 1994, 32(8): 1598-1605.

[20] SRINIVASAN G R, BAEDER J D. Flowfield of lifting rotor in hover: A Navier-Stokes simulation[J]. AIAA Journal, 1992, 30(10): 2371-2378.

[21] KIM J W, PARK S H, YU Y H. Euler and Navier-Stokes simulations of helicopter rotor blade in forward flight using an overlapped grid solver: AIAA-2009-4268[R]. Reston, VA: AIAA, 2009.

[22] ANANTHAN S, BAEDER J, SIM B W, et al. Prediction and validation of the aerodynamics, structure dynamics, and acoustics of the SMART rotor using a loosely-coupled CFD-CSD analysis[C]∥American Helicopter Society 66th Annual Forum. Alexandria, VA: The AHS International, Inc., 2010: 2031-2057.