适用于非周期流固耦合问题的时间谱方法

杨体浩，白俊强，史亚云，杨一雄

西北工业大学 航空学院，西安 710072

飞行器设计是涉及气动、结构、控制和飞行力学等其他学科在内的复杂的多学科问题。通常这些学科之间会相互耦合，尤其是气动与结构之间会产生明显的流固耦合现象，除了静气动弹性变形以外，还包括颤振等在内的动气动弹性现象[1-2]。这些流固耦合现象会对飞行器的性能、稳定性和安全性造成显著的影响。随着现代飞行器展弦比的不断增大以及机翼柔性的增加，气动、结构之间的耦合问题也变的越来越突出[3]。这使得发展高效、准确的动气动弹性仿真、分析工具以及考虑动气动弹性影响(如颤振边界)的气动/结构多学科优化设计系统成为决定未来先进飞行器的研制能否成功的关键因素之一。

直接将计算流体力学(Computational Fluid Dynamics, CFD)程序与计算结构动力学(Computational Structural Dynamics, CSD)程序耦合，建立一套时域的气动、结构仿真分析和优化设计工具是最直接的方式。但是，这种基于高精度求解器的时域方法需要花费大量的计算时间，无法满足实际的工程应用需求。因此，针对考虑动气动弹性影响的气动/结构优化设计与分析问题，需要发展新的方法以提高计算效率。

目前针对非定常问题，降阶模型(Reduced-Order Model, ROM)被视为一类很有应用价值的方法。在气动弹性以及优化设计领域，本征正交分解(Proper Orthogonal Decomposition, POD)[4]是一种最为常见的降阶模型。POD以一组基于最小二乘思想的正交基去近似高维问题。但是POD模型的建立需要采集样本快照，借助高精度的CFD求解器生成样本快照需要花费大量的计算时间，这在一定程度上降低了POD的计算效率。除此之外，包括POD在内的许多降阶模型缺乏对系统参数变化的鲁棒性，比如马赫数、结构参数和机翼型面等参数的变化[5]。系统可变参数的个数越多，参数变化范围越大，降阶模型的精度和鲁棒性越差。然而，许多实际的工程应用问题包含了大量的可变参数。因此，借助降阶模型难以对具有大量变参的系统进行可靠的灵敏度分析。这也使得在优化设计领域，无法将降阶模型与基于梯度信息的高效优化设计方法相结合，如伴随方法[6]。

针对非定常问题，谐波平衡(Harmonic Balance, HB)[7]是另一种很有吸引力的方法。HB通过将系统控制方程的状态变量用截断的傅里叶系数进行替换，最终将非定常的控制方程转化为耦合的定常控制方程。HB直接对系统控制方程进行处理，不需要样本快照。因此，HB具有很高的计算精度和鲁棒性。借助HB方法，可以准确地对整个系统进行灵敏度分析，并且很容易与伴随方法耦合对非定常问题进行优化设计，大大地提高优化设计效率。Choi等[8]将HB与伴随方相结合建立了非定常气动伴随优化设计系统，并以此对直升机旋翼进行了气动外形优化设计。但是，HB方法只适用于周期性的非定常问题，具有一定的局限性，而很多实际的流固耦合问题都是非周期的。

除了降阶模型和HB方法，采用效率更高的低精度方法是另一种选择。这类方法控制方程形式简单，求解速度快，非常适用于飞行器概念设计以及初始设计阶段。通过耦合修正模型，针对很多非定常问题，低精度方法都可以达到期望的计算精度。Timme[9]利用耦合了全速势方程和非定常边界层方程的求解器，对跨声速机翼进行了气动弹性稳定性研究。研究结果表明，当不存在明显的流动分离时，全速势方程计算的结果与基于非定常雷诺平均Navier-Stokes(URANS)方程的计算结果以及实验数据都较为接近。对于低亚声速问题，基于势流理论的流固耦合分析方法被广泛的用来研究包括经典颤振问题在内的多种动气动弹性问题。NASTRAN就是一种被广泛应用于气动弹性问题研究的基于势流理论的商业软件[10]。Hesse和Palacios[11]利用非定常涡格法和复合材料梁有限元模型对大柔性飞行器的飞行动力学问题进行了成功的研究。

除此之外，基于势流理论的流固耦合分析方法还被广泛的与其他优化设计技术相结合，进行考虑动气动弹性影响的优化设计研究。Haghighat等[12]利用涡格法、梁有限元模型和智能优化算法针对大展弦比柔性机翼进行了考虑阵风减缓的多学科优化设计研究。Stanford和Beran[13]利用Theodorsen气动力模型、非线性梁有限元模型和ONERA动失速修正模型，借助设计手段，通过优化结构质量和刚度分布去改变大展弦比柔性机翼的颤振边界和极限环振荡(Limit Cycle Oscillation, LCO)特性。Mallik等[14]利用非线性结构有限元模型和考虑了压缩性修正的Theodorsen气动力模型进行颤振边界的计算，并借助遗传算法将其与传统针对静力学问题的气动/结构多学科优化设计系统相结合，针对支撑翼(Truss-Braced Wing, TBW)布局飞机探讨了颤振约束对设计结果的影响。其研究结果表明，针对TBW，是否考虑颤振约束对整个优化设计结果的性能有较为明显的影响。

目前国际上，在考虑了动气动弹性影响(尤其是颤振边界)的优化设计领域方面，主流的做法还是利用频域法或者直接时域法进行动气动弹性特性的计算分析，然后借助智能算法将其引入到优化设计过程中。这种借助智能算法的优化设计方法计算量很大，尤其是当整个系统的设计变量个数较多，或者优化设计系统的静力学问题部分采用高精度求解器的时候。除此之外，也有一部份学者直接把伴随方法与传统的时域流固耦合分析方法进行结合，将动气动弹性的影响引入到气动结构多学科优化设计中。如，Zhang等[15]基于Euler和复杂有限元模型求解器，建立了针对非定常流固耦合问题的伴随优化设计系统，并对M6机翼进行了考虑颤振约束的气动结构多学科优化设计研究。虽然伴随方法的采用克服了基于智能算法的优化设计系统的缺点，但是直接将伴随方法与传统的时域流固耦合求解方法相结合的处理方式，需要在每一个时间推进步上求解伴随方程。通常非定常流固耦合问题的时域推进求解过程需要成百上千甚至更多的时间推进步，这意味着采取直接耦合的方式需要进行成百上千甚至更多次的伴随方程的求解，整个求解过程计算量很大，大大削弱了基于伴随方法的气动/结构多学科优化设计系统的计算效率。因此，需要发展新的方法，以显著提针对非定常流固耦合多学科设计问题的伴随优化设计系统的计算效率。

在飞行器设计领域，针对非定常流固耦合问题建立高效、可靠的设计、分析工具十分必要。然而，现有的方法都无法很好地满足这一需求。针对这一问题，本文的主要研究目的是针对一般运动形式的低亚声速问题，将Chebyshev谱方法与基于非定常面元法、几何非线性梁有限元模型的流固耦合分析方法进行耦合，建立面向考虑动气动弹性影响(主要考虑经典颤振问题)的气动/结构一体化设计的，可与伴随方法相结合的高效、可靠的流固耦合分析方法。Chebyshev谱方法直接对流固耦合控制方程进行处理，将非定常问题转化为在选取的Chebyshev控制点处耦合的定常问题。因此，与HB方法类似，Chebyshev谱方法具有较高的计算精度和可靠性，并且很容易与伴随方法结合建立针对非定常流固耦合问题的伴随优化设计系统。由于Chebyshev谱方法将非定常问题转化为在选取的Chebyshev控制点处耦合的定常问题进行求解，因此在与伴随方法进行结合时，只需在选取的Chebyshev控制点处进行伴随方程的求解即可，以此大大地节省计算量提高优化设计效率。但是与HB方法不同的是，Chebyshev谱方法不仅适用于周期性问题，还适用于非周期性问题。Choi等[16-17]将Chebyshev谱方法与URANS求解器相结合进行了非定常气动力的计算分析，得到了令人满意的求解精度。虽然，他成功地利用Chebyshev谱方法进行了非定常气动力的计算分析，但是目前其研究成果具有比较明显的局限性，距离实现Chebyshev谱方法与伴随方法相结合进行非定常流固耦合问题优化设计的目标还较远。一方面，Choi等引入的是周期性边界条件，这意味着虽然采用的是Chebyshev谱方法，但是处理的依旧是达到了稳定状态的周期性非定常问题，而自然界中很多现象是非周期性的；另一方面，Choi等仅仅将Chebyshev谱方法与非定常气动模型进行了耦合，还没有将其与结构动力学模型进行耦合建立相应的流固耦合分析方法。相比之下，本文将Chebyshev谱方法同时与非定常气动力模型以及结构动力学模型进行耦合，建立了相应的流固耦合分析方法。同时，向系统中引入初始条件而非周期性边界条件，使得所建立的流固耦合分析方法可以计算非定常问题的瞬态响应，即适用于周期性非定常问题也适用于非周期性的非定常问题。

本文面向大展弦比飞行器的非定常流固耦合多学科优化设计问题，采用将Chebyshev谱方法与基于非定常面元法和几何非线性梁有限元模型的流固耦合分析方法进行结合，建立了针对低亚音速流动的高效、可靠的，可与伴随方法相结合的流固耦合分析方法。所建立的分析方法主要针对不考虑气动非线性的动气动弹性问题，如经典的颤振问题。通过Goland机翼颤振速度的计算对建立的基于Chebyshev谱方法的流固耦合分析系统的精度、可靠性和收敛性等特点进行了探讨研究。

1 Chebyshev谱方法

1.1 标准的Chebyshev谱方法

Chebyshev谱方法是一种以Chebyshev多项式插值为理论基础的时间谱方法[18]。理论上，任意一个定义在时间区间[-1,1]内的光滑函数u(t)，在tm时刻的函数值可以表示为

(1)

Ti(tm)=cos(icos-1(tm))i=0,1,…,N

(2)

(3)

式中：Ti为Chebyshev多项式;ai为Chebyshev系数;N为在时间区间[-1,1]内选取的Chebyshev控制点的个数。显然，一旦Chebyshev控制点处的函数值已知，那么在定义的时间区间内，任意时刻的函数值可以通过式(1)求得。

进一步，函数u(t)在Chebyshev控制点处的时间导数可以推导为

(4)

(5)

(6)

(7)

1.2 Chebyshev算子的投影变换

Chebyshev控制点在时间区间内的分布情况会对其计算结果的精度产生一定的影响。标准的Chebyshev谱方法的控制点在时间区间的两端分布较为密集，这种分布形态使得标准的Chebyshev谱方法需要更多的控制点个数去达到期望的计算精度[19]。因此，采用Kosloff和Tal-Ezer[20]提出的投影变换函数改变Chebyshev谱方法的控制点分布，使其分布更为均匀。投影变换的表达式为

(8)

通常对于实际的非定常问题，时间区间是[t0,tt]而不是[-1,1]，因此需要通过等价变换将时间区间从[t0,tt]变化到[-1,1]。采用线性变换函数：

(9)

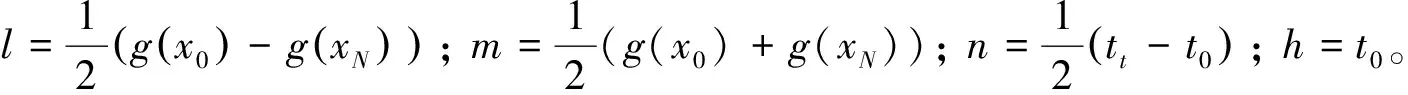
(10)

1.3 验证算例

经过投影变换的Chebyshev算子被称为投影的Chebyshev算子(Mapped Chebyshev Operator，MCO)。利用非周期的三角函数验证投影的Chebyshev算子的计算精度，揭示投影的Chebyshev谱方法的数学特性。三角函数的表达式为

(11)

(12)

图1为具有3种不同Chebyshev控制个数的投影的Chebyshev算子的计算结果与解析解的对比，其中图1(a)为计算得到的函数值u的对比，图1(b)为计算得到的函数值u相对于解析解uAnalytic的绝对误差对比。图2为Chebyshev控制点在定义的时间区间内的分布示意图。显然，投影的Chebyshev算子的计算精度随着Chebyshev控制点个数的增加而不断增大。当控制点的个数增加到14，投影的Chebyshev算子的计算结果几乎与解析解重合。

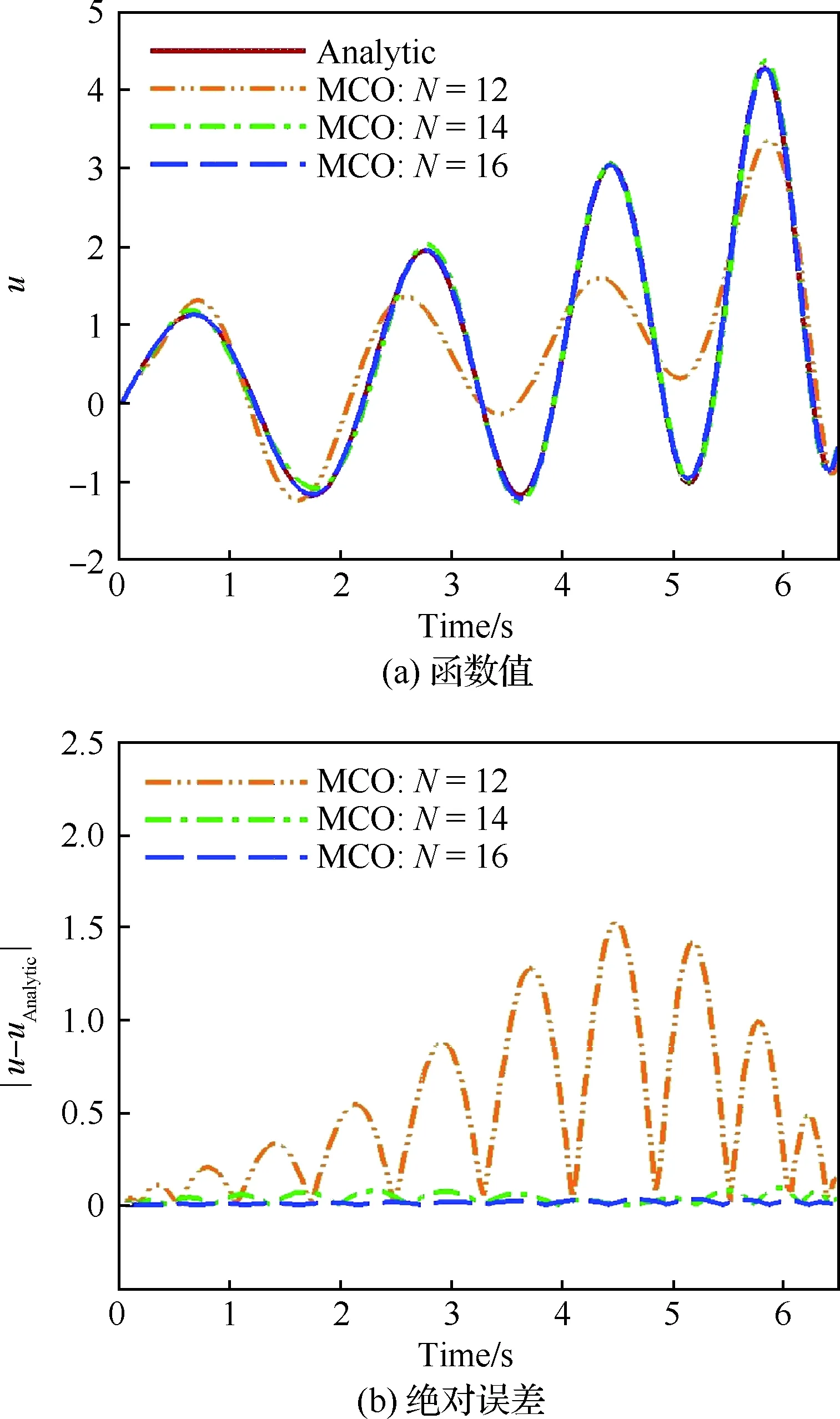
图1 投影的Chebyshev算子的计算结果与解析解的对比Fig.1 Comparisons between results obtained from mapped Chebyshev operator and analytic solution

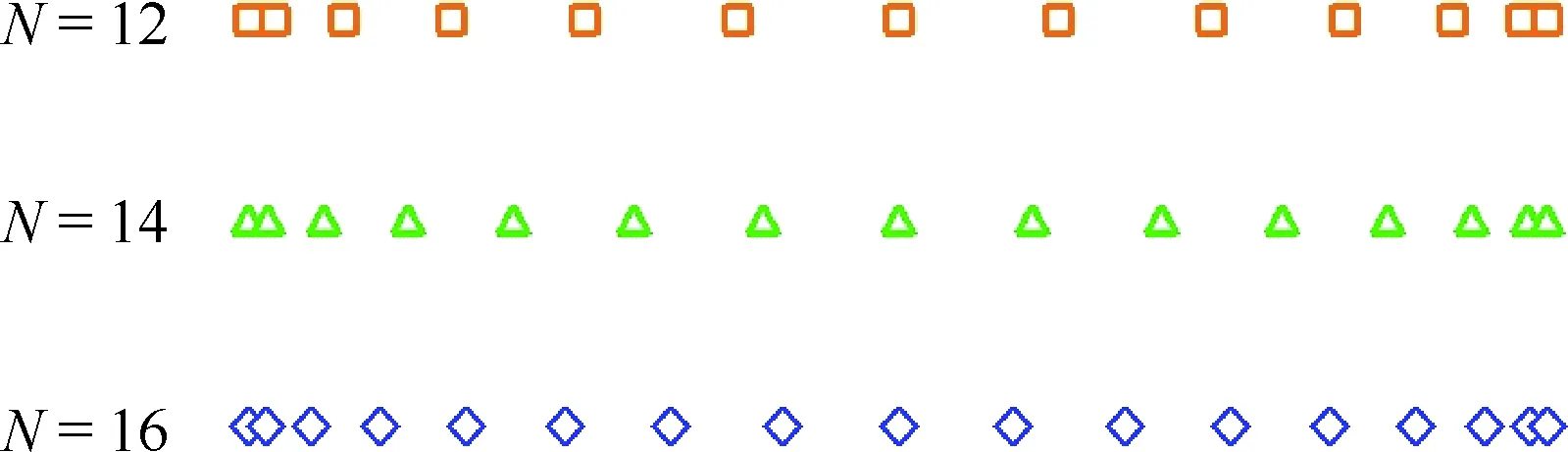
图2 投影的Chebyshev控制点分布Fig.2 Distribution of mapped Chebyshev control points

计算结果表明，即便对于非周期函数，Chebyshev算子也可以用较少的控制点的个数得到满足精度要求的计算结果。

2 基于投影的Chebyshev谱方法的非定常气动力模型

2.1 非定常面元法

非定常面元法由Laplace方程推导演化而来。本文采用具有定常面元强度的非定常面元法[21]，并且忽略黏性等气动非线性的影响。其在(n+1)dt时刻的控制方程为

(13)

(14)

(15)

(16)

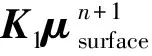
图3 尾迹模型Fig.3 Wake model

通过控制方程可以求出物面面元的强度，进而作用在物面面元上的压力系数可以通过式(17)获得：

(17)

式中：Cpk为第k个物面面元控制点处的压力系数；pk和pref分别为作用在第k个物面面元控制点处的静压和无穷远处自由来流的静压；ρ为大气密度；Qk为第k个物面面元控制点处的当地流体速度；Φk为第k个物面面元控制点处的速度势。

2.2 非定常面元法与Chebyshev谱方法的耦合

根据Chebyshev谱方法的理论可知，将Chebyshev谱方法与非定常面元法结合以后，只有在Chebyshev控制点处的状态变量为待求未知变量。显然，在给定的时间区内的任意时刻，物面的运动速度和位置形状可表示为

(18)

(19)

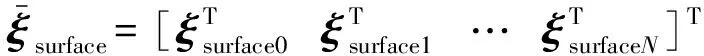
根据尾迹形状的递推关系式(式(16))可知，在ti=t0+ndt时刻，尾迹的形状为

μwake,μsurface,σsurface,Vgust)

(20)

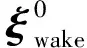
(21)

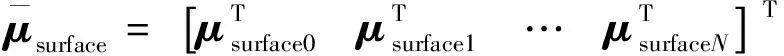
(22)

(23)

(24)

(25)

(26)

显然，当初始条件给定后，通过迭代求解上述控制方程可以获得在选定的Chebyshev控制点处的面元的强度。进而借助Chebyshev算子可以计算得到定义的时间区间内任一时刻下的面元强度。联立式(10)与式(17)可计算得到对应状态下所有物面面元的压力系数：

(27)

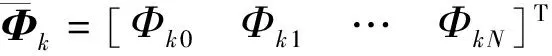
2.3 验证算例

选取做非周期强迫俯仰运动的大展弦比等直机翼作为验证耦合了Chebyshev谱方法的非定常面元法计算精度的算例。机翼由NACA0012翼型成型，展弦比为36，物面面元的划分如图4所示。强迫的俯仰运动迎角为

(28)

式中:迎角α0=0°;运动周期T=0.4 s。等直机翼以过50%弦点的平行于前缘的直线为轴做俯仰运动。

图5为Chebyshev谱方法(Chebyshev Spec-tral Method, CSM)与传统的时间推进方法计算得到的非定常气动力系数对比图。Chebyshev谱方法的控制点的个数为18。计算结果显示，无论是升力系数CL还是力矩系数Cm，Chebyshev谱方法的计算结果与传统的时间推进方法所得到的结果都有很好的吻合度。显然，针对非周期问题，耦合了Chebyshev谱方法的非定常面元法能够以较少的控制点个数获得具有足够精度的计算结果。

图4 机翼表面面元Fig.4 Surface panels of wing

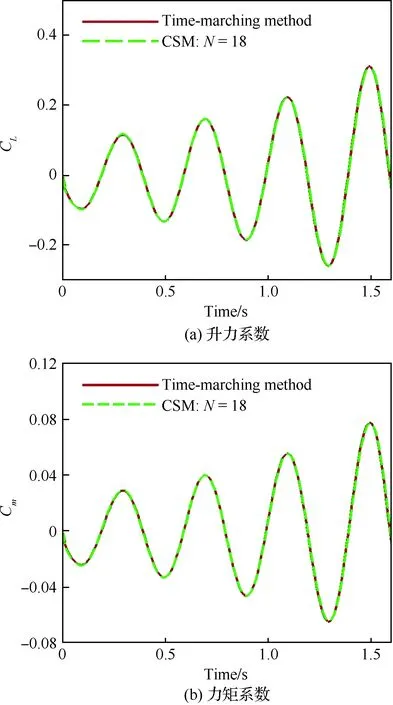
图5 Chebyshev谱方法与时间推进方法计算得到的非定常气动力对比Fig.5 Comparison of unsteady aerodynamic forces calculated by Chebyshev spectral method and time-marching method

3 基于Chebyshev谱方法的结构动力学模型

3.1 几何非线性梁有限元模型

采用基于旋转矢量的几何非线性梁有限元模型进行结构动力学建模[22]。相比于复杂有限元模型，梁模型自由度很少，形式简单，非常适用于飞行器概念以及初始设计阶段的多学科问题的研究。对于传统的大展弦比机翼(如B737机翼)，线性梁有限元模型能够较为准确地捕捉机翼结构的静力学和动力学行为。但是对于展弦比更大的柔性机翼(如美国NASA的“Helios”太阳能无人机)，在典型的使用工况下机翼结构便表现出明显的几何非线性特性。这种情况下，线性梁有限元模型已经不再适用，需要借助几何非线性梁有限元模型。这类大展弦比、大柔性机翼虽然发生大变形，但是主要是弯曲大变形，而扭转变形相对较小，对于诸如经典颤振问题这类动气动弹性问题而言，线性气动力模型依然适用。因此，为使所建立的方法更具一般性，本文采用可考虑几何非线性的梁有限模型进行结构动力学建模，并将其与线性非定常气动力模型耦合，针对大展弦比机翼进行不考虑气动非线性的流固耦合问题研究，如经典的颤振问题。

基于旋转矢量的几何非线性梁有限元模型采用矢端向量RG(s,t)和笛卡尔旋转矢量(Cartesian Rotation Vector，CRV)ψ(s,t)[23]作为描述梁模型上任意一点的位移以及扭转变形自由度,其中s为在梁参考线上定义的弧长坐标，t表示时间。坐标系的定义如图6所示。

图6 坐标系的定义Fig.6 Definition of coordinate systems

t时刻梁模型上任意一点，相对于未变形构型(即t=0时刻的构型)的应变可表示为

(29)

式中：γ和κ分别为线应变和角应变；CBG表示从惯性坐标系G到材料坐标B的坐标变换矩阵；(·)′表示相对于弧长坐标s的导数；KB(s,t)=T(ψ)ψ′，T(ψ)为切向算子[22]。

根据Hamilton原理有：

(30)

(31)

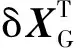
(32)

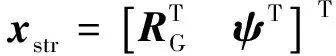
(33)

式中：M、C和K分别为切向质量矩阵、切向阻尼矩阵和切向刚度矩阵。考虑几何非线性时，M、C和K不是常值矩阵，而是与状态变量相关的函数。基于增量形式的结构动力学方程，利用相应的数值求解方法(如Newton-Raphson方法)进行迭代求解，即可获得梁模型的结构动力学响应。

3.2 几何非线性梁有限元模型与Chebyshev谱方法的耦合

几何非线性梁有限元模型可以写成结构动力学方程的一般形式：

(34)

通过等价变换将二阶微分方程转化为一阶微分方程：

(35)

(36)

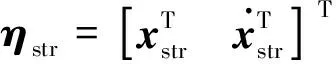
(37)

(38)

(39)

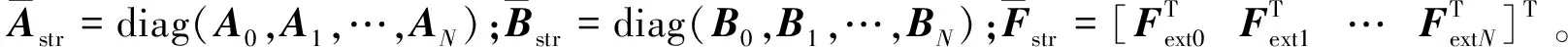
显然，借助Chebyshev谱方法，非定常形式的结构动力学模型被转化为在选定的Chebyshev控制点处的定常方程。当给定初始条件后，通过迭代求解控制方程可以获得结构状态变量在所有Chebyshev控制点处的值。之后，利用Chebyshev算子可以计算得到在给定时间区间内的结构动力学响应。

3.3 验证算例

选取端部承受强迫载荷的悬臂梁(见图7)作为验证耦合了Chebyshev谱方法的几何非线性梁有限元模型的计算精度的算例。悬臂梁长l=16 m，结构属性见表1。强迫载荷F的方向竖直向上，在整个时间历程中方向保持不变，力的大小随着时间呈现如图8所示的变化(图中Famp为强迫载荷F允许的最大幅值)。

图7 施加强迫载荷的悬臂梁Fig.7 Cantilever beam with forced load

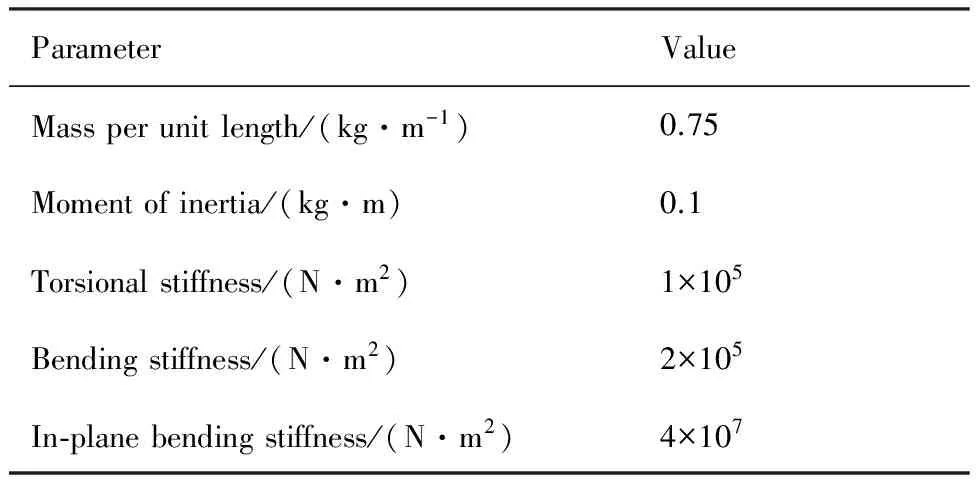
表1 梁结构属性Table 1 Properties of beam structure

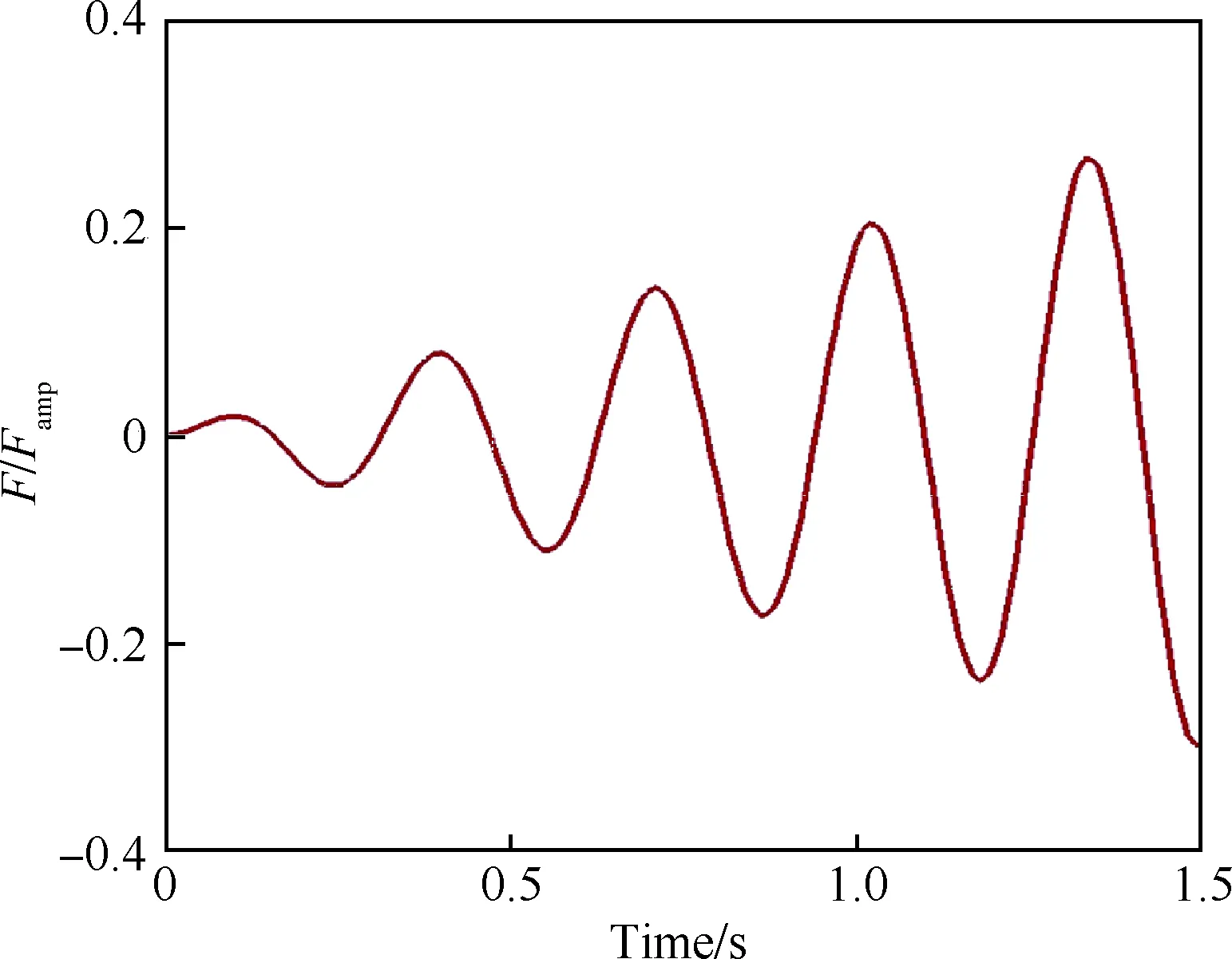
图8 强迫载荷的时间历程Fig.8 Time history of forced load

图9为Chebyshev谱方法与传统的时间推进方法计算得到的结构动力学响应(梁端部的挠度变形Z以及纵向速度Vz响应)对比图。其中Chebyshev谱方法的控制点的个数为18，时间推进方法的时间步长为0.001 s。计算结果表明，无论是位移响应还是速度响应，Chebyshev谱方法的计算结果都几乎与时间推进方法的计算结果重合。显然，耦合了Chebyshev谱方法的几何非线性梁有限元模型，借助有限的控制点个数，便可以以足够高的精度准确地捕捉整个结构系统的动力学特性。

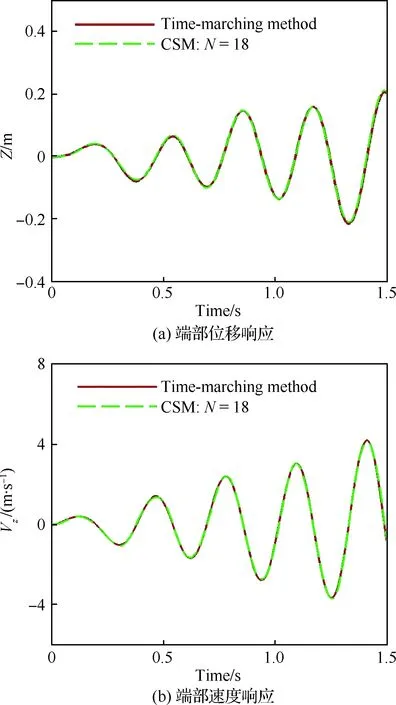
图9 Chebyshev谱方法与时间推进方法计算得到的结构动力学响应对比Fig.9 Comparison of structural dynamic response calculated by Chebyshev spectral method and time-marching method

4 基于Chebyshev谱方法的流固耦合分析系统

利用松耦合迭代策略求解基于Chebyshev谱方法的流固耦合控制方程。由于Chebyshev谱方法分别与非定常气动力模型以及结构动力学模型相结合，将非定常的流固耦合问题转化为在选定的Chebyshev控制点处耦合的定常问题。因此，基于Chebyshev谱方法的动气动弹性问题的求解过程，类似于传统采用松耦合策略的静气动弹性问题的求解，只不过所有Chebyshev控制点处的控制方程是同时求解的。这种不同Chebyshev控制点处，控制方程的耦合实际上是整个时间响应历程内不同Chebyshev控制点处的状态变量之间时间依赖性的直接体现。

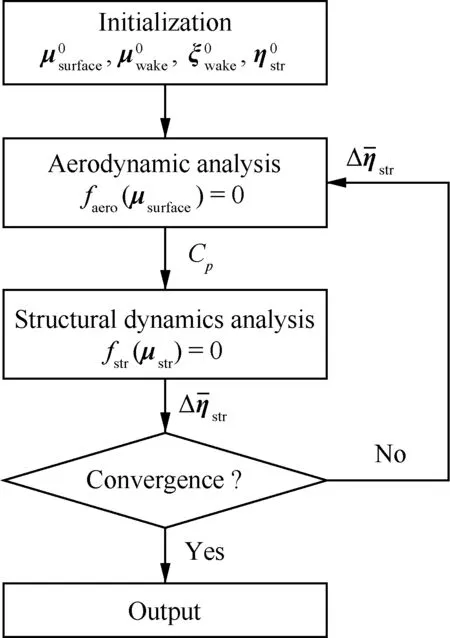
图10 基于Chebyshev谱方法的流固耦合问题求解流程Fig.10 Calculation flow chart of fluid-structure coupling problems based on Chebyshev spectral method

5 数值仿真与讨论

对标准模型Goland机翼[24]进行颤振速度的计算，以验证本文搭建的基于Chebyshev谱方法的流固耦合计算、分析方法的收敛特性及计算精度。Goland机翼半展长6.096 m，弦长1.828 8 m。采用国际上针对Goland机翼计算分析使用的梁有限元相关参数[24]，具体的结构属性如表2所示。图11为Goland机翼表面面元的划分。

图12为Chebyshev谱方法与时间推进方法计算得到的不同自由来流速度V∞下的翼尖挠度变形Z的动力学响应对比图。Chebyshev谱方法的控制点个数为22。Goland机翼的初始迎角为0°，在t=0 s时刻，给Goland机翼施加一个大小为0.055°的小迎角扰动。计算结果显示，在172 m/s的自由来流速度下，Goland机翼的振动成发散的趋势。当自由来流速度减小到167.5 m/s时，Goland机翼维持等幅地周期性振动。在两种不同的自由来流速度下，Chebyshev谱方法的计算结果都几乎与时间推进方法(图中“Time-marching Method”表示采用传统的时间推进方法，计算得到的流固耦合系统在给定初始条件下的瞬态响应)的所得结果完全重合。因此，本文建立的基于Chebyshev谱方法的流固耦合计算、分析方法能够比较准确地捕捉流体与固体之间的瞬态响应。

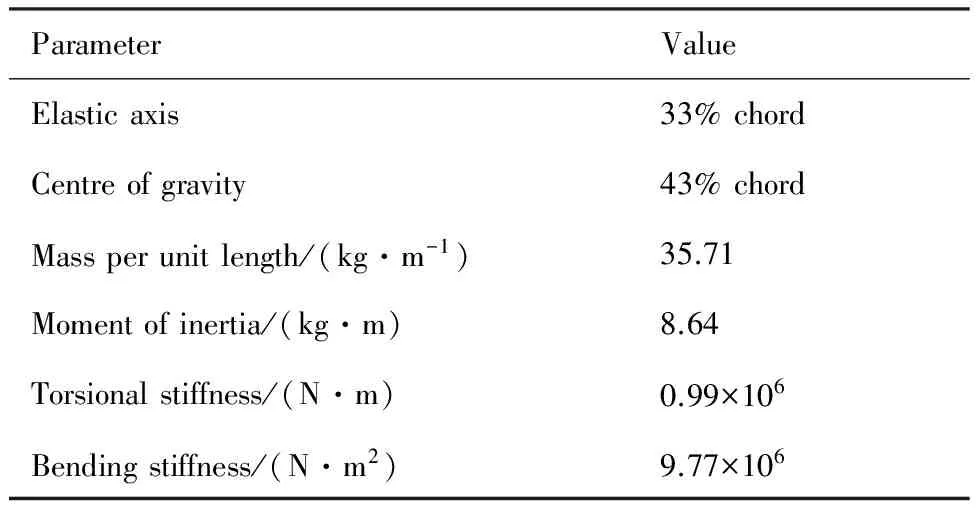
表2 Goland机翼属性Table 2 Properties of Goland wing

图11 Goland机翼表面面元Fig.11 Surface panels of Goland wing

表3为不同模型计算得到的Goland机翼颤振速度Vf的对比。显然，相比于Patil等[25]利用片条理论计算得到的Goland机翼的颤振速度，本文的计算结果与采用几何非线性梁有限元模型和非定常涡格法的SHARP程序[22]的计算结果更为接近，颤振速度相差不超过1%。基于片条理论得到的Goland机翼颤振速度偏低的主要原因在于经典的片条理论无法捕捉三维效应。对比结果显示，本文基于Chebyshev谱方法、非定常面元法和几何非线性梁有限元模型所建立的流固耦合计算方法具有足够的可信度。

图13为采用了松耦合求解策略的Chebyshev谱方法的收敛历程。其中Iterarion=0表示给定的系统初值。计算结果显示，经过大约8次迭代以后，基于Chebyshev谱方法的流固耦合计算方法便达到了收敛。收敛历程显示，整个迭代过程呈现出从初始时刻向终了时刻逐步收敛的趋势。其原因在于本文所处理的流固耦合问题为初值问题。初始条件所包含的信息随着迭代计算逐步向时间下游传递。

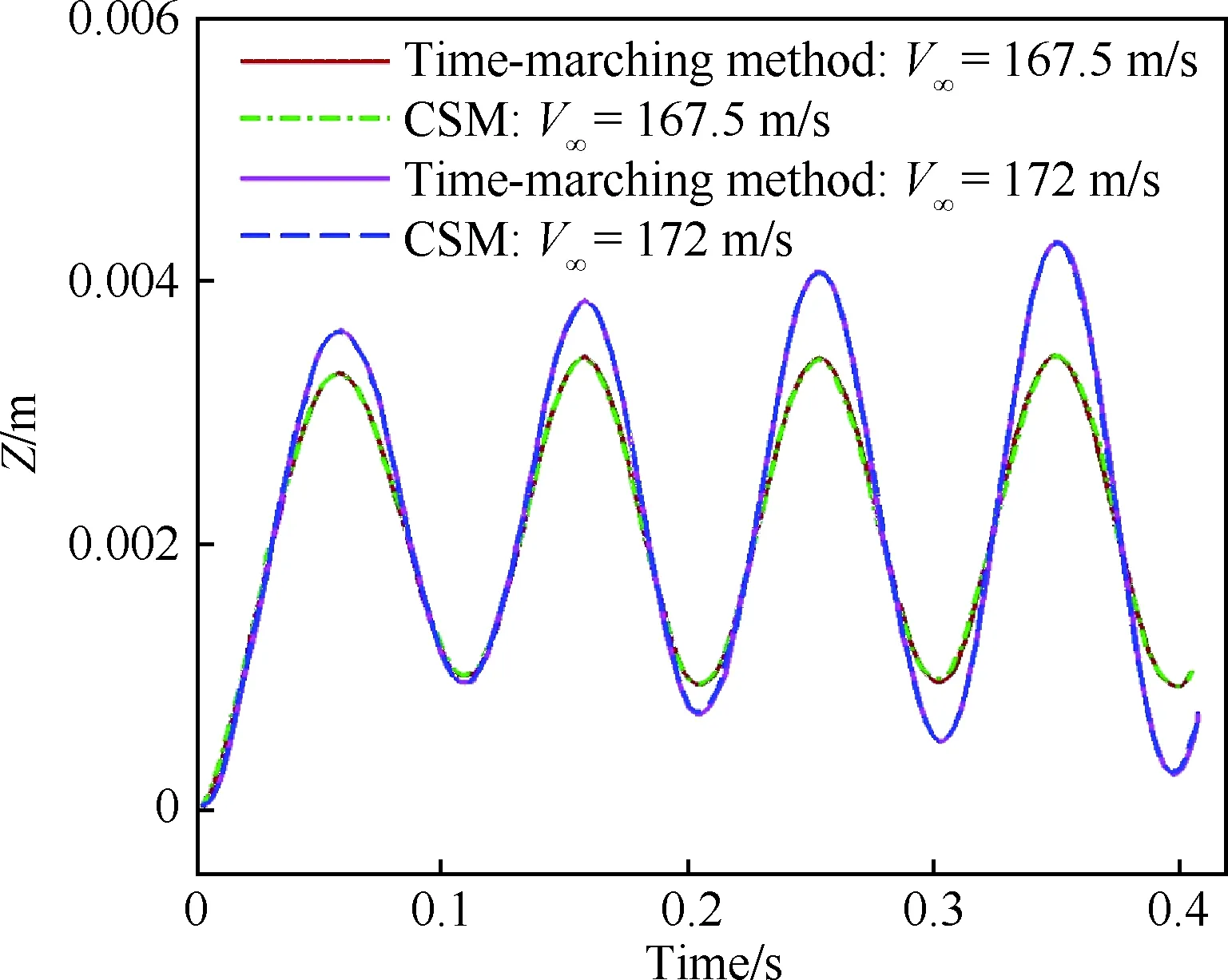
图12 不同自由来流速度下的Goland机翼翼尖时间历程响应对比Fig.12 Comparison of time history of Goland wing tip at various free-stream velocities

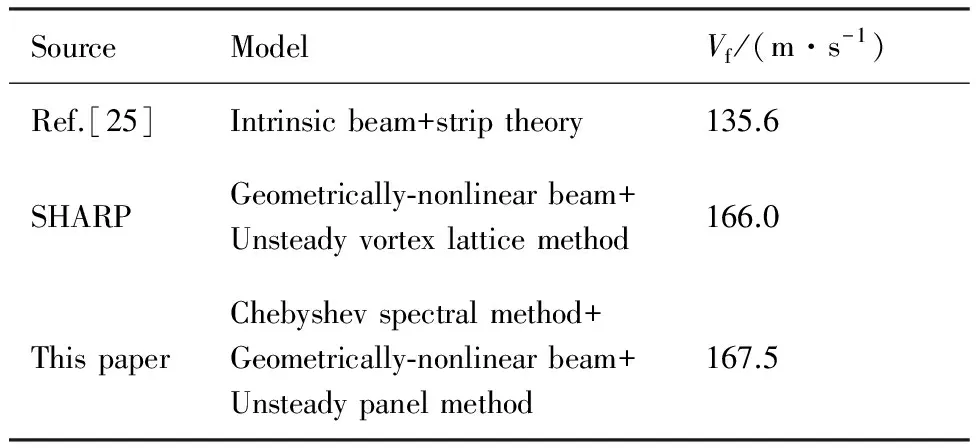
表3 Goland机翼颤振速度对比Table 3 Comparison of flutter speed of Goland wing

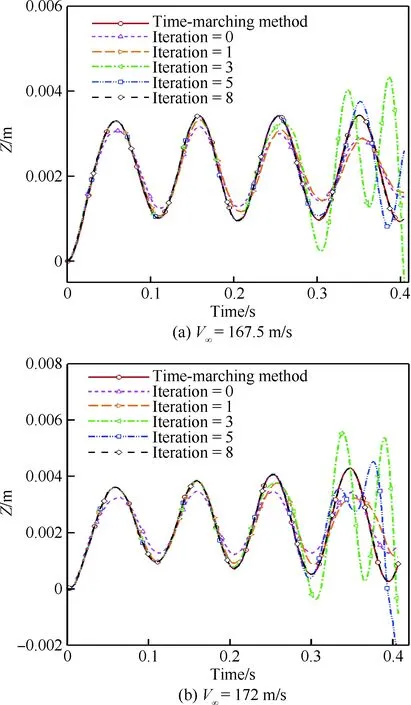
图13 Chebyshev谱方法的收敛历程Fig.13 Convergence process of Chebyshev spectral method

6 结 论

1) Chebyshev谱方法利用Chebyshev算子替换系统的状态变量及其导数，将非定常问题转化为选取的Chebyshev控制点处耦合的定常问题进行处理。由于Chebyshev谱方法直接对流固耦合的控制方程进行处理，因此所建立的基于Chebyshev谱方法的流固耦合计算、分析方法具有较强的鲁棒性。

2) Chebyshev谱方法的计算精度随着Chebyshev控制点个数的增加而不断提高，测试算例表明，只需少许有限的Chebyshev控制点，Chebyshev谱方法便可以达到期望的计算精度。

3) Chebyshev谱方法具有较强的适用性，不仅适用于周期性非定常问题还适用于非周期性非定常问题。

4) 建立的基于Chebyshev谱方法的流固耦合分析方法能够准确地捕捉流体与结构之间的耦合作用，可用于忽略了气动非线性的流固耦合问题的计算、分析与设计研究，如经典的颤振问题。

参 考 文 献

[1] LIVNE E, WEISSHAARW T A. Aeroelasticity of nonconventional airplane configurations-past and future[J]. Journal of Aircraft, 2003, 40(6): 1047-1065.

[2] XIANG J, YAN Y, LI D. Recent advance in nonlinear aeroelastic analysis and control of the aircraft[J]. Chinese Journal of Aeronautics, 2014, 27(1): 12-22.

[3] SU W, CESNIK C E S. Strain-based geometrically nonlinear beam formulation for modeling very flexible aircraft[J]. International Journal of Solids and Structures, 2011, 48(16): 2349-2360.

[4] LIEU T, FARHAT C. POD-based aeroelastic analysis of a complete F-16 configuration: ROM adaptation and demonstration: AIAA-2005-2295[R]. Reston, VA: AIAA, 2005.

[5] AMSALLEM D, FARHAT C. Interpolation method for adapting reduced-order models and application to aeroelasticity[J]. AIAA Journal, 2008, 46(7): 1803-1813.

[6] LYU Z, KENWAY G K, PAIGE C, et al. Automatic differentiation adjoint of the reynolds-averaged navier-stokes equations with a turbulence model: AIAA-2013-2581[R]. Reston, VA: AIAA, 2013.

[7] HALL K C, THOMAS J P, CLARK W S. Computation of unsteady nonlinear flows in cascades using a harmonic balance technique[J]. AIAA Journal, 2002, 40(5): 879-886.

[8] CHOI S, LEE K, POTSDAM M M, et al. Helicopter rotor design using a time-spectral and adjoint-based method[J]. Journal of Aircraft, 2014, 51(2): 412-423.

[9] TIMME S. Transonic aeroelastic instability searches using a hierarchy of aerodynamic models[D]. Liverpool: University of Liverpool, 2010.

[10] PERERA M, GUO S. Structural and dynamic analysis of a seamless aeroelastic wing: AIAA-2010-2878[R]. Reston, VA: AIAA, 2010.

[11] HESSE H, PALACIOS R. Reduced-order aeroelastic models for dynamics of maneuvering flexible aircraft[J]. AIAA Journal, 2014, 52(8): 1717-1732.

[12] HAGHIGHAT S, RA MATRINS J R, LIU H H. Aeroservoelastic design optimization of a flexible wing[J]. Journal of Aircraft, 2012, 49(2): 432-443.

[13] STANFORD B, BERAN P. Direct flutter and limit cycle computations of highly flexible wings for efficient analysis and optimization[J]. Journal of Fluids and Structures, 2013, 36: 111-123.

[14] MALLIK W, KAPANIA R K, SCHETZ J A. Effect of flutter on the multidisciplinary design optimization of truss-braced-wing aircraft[J]. Journal of Aircraft, 2015, 52(6): 1858-1872.

[15] ZHANG Z, CHEN P C, WANG Q, et al. Adjoint based structure and shape optimization with flutter constraints: AIAA-2016-1176[R]. Reston, VA: AIAA, 2016.

[16] IM D K, CHOI S, MCCLURE J E, et al. Mapped Chebyshev pseudospectral method for unsteady flow analysis[J]. AIAA Journal, 2015, 53(12): 3805-3820.

[17] CHOI J Y, CHOI S, PARK J, et al. Prediction of dynamic Stability using mapped Chebyshev pseudospectral method: AIAA-2016-1347[R]. Reston, VA: AIAA, 2016.

[18] MOIN P. Fundamentals of engineering numerical analysis[M]. Cambridge: Cambridge University Press, 2010.

[19] BAYLISS A, TURKEL E. Mappings and accuracy for Chebyshev pseudo-spectral approximations[J]. Journal of Computational Physics, 1992, 101(2): 349-359.

[20] KOSLOFF D, TAL-EZER H. A modified Chebyshev pseudospectral method with anO(N-1) time step restriction[J]. Journal of Computational Physics, 1993, 104(2): 457-469.

[21] KATZ J, PLOTKINP A. Low-speed aerodynamics[M]. Cambridge: Cambridge University Press, 2001.

[22] MURUA J. Flexible aircraft dynamics with a geometrically-nonlinear description of the unsteady aerodynamics[D]. London: Imperial College London, 2012.

[23] GERADIN M, CARDONA A. Flexible multibody dynamics: A finite element approach[M]. 2001.

[24] GOLAND M. The flutter of a uniform cantilever wing[J]. Journal of Applied Mechanics, 1945, 12(4):197-208.

[25] PATIL M J, HODEGES D H, CESNIK C E S. Nonlinear aeroelastic analysis of complete aircraft in subsonic flow[J]. Journal of Aircraft, 37(5): 753-760.