考虑多源采购的产品族供应链优化配置方法

（1.广东工业大学 广东省计算机集成制造重点实验室，广东 广州 510006；2.暨南大学 电气信息学院，广东 珠海 519070；3.华南农业大学 数学与信息学院，广东 广州 510642）

随着经济全球化，市场竞争日益激烈，顾客需求越来越多样化，为最大程度满足顾客的需求以在市场中取得优势，企业不得不根据细分市场设计出多种产品。产品种类的增加导致供应链网络愈加复杂，产品生产费用库存成本高，上市时间长。许多企业为了缩短上市时间，达到产品种类跟规模经济的平衡，纷纷采用产品平台策略，设计面向不同细分市场的产品族。

产品族（productfamily）是为了满足不同客户需求基于产品平台得到的一组相关产品变种[1]。产品平台是由所有产品变种共享的公共组件和生产过程的集合。通过以平台为基础的产品族开发，企业可以有效地开发多样化产品，提高其生产过程的灵活性和响应能力。运用产品平台而设计出的产品族供应链拥有显著优点。例如，由于来自多个产品的不确定需求的相互抵消，共享平台阶段的安全库存可能会减少[2-4]。这通常被称为风险统筹效应。因此，越来越多的学者开始研究基于产品平台的开发和供应链决策问题。

在战略阶段，对于给定的供应链网络，企业面临一系列决策来配置网络各个阶段或节点。供应链网络的每个节点都有几个可供选择的备选选项完成其功能并作为库存的潜在库存点。决定每个节点哪个选项被选择以及库存设置在哪个节点被称为供应链配置。供应链配置的范围包含了一个制造企业内部及外部的生产流程配置。因此，供应链配置不仅包括哪些可选择供应商或节点被选择、不同层级上的节点设置多少库存，而且还包括制造工艺方面如加工方法的使用，生产提前期、上市时间。人们普遍认为产品设计决策和相关的供应链是相互关联的。然而，当平台产品被考虑时，很少研究直接指出它们是怎么相互影响的。

Graves等在考虑企业产能无限、单源采购的情况下，采用基本库存策略，以模式选择和服务时间作为决策变量，建立了以最小化供应链总成本为目标的供应链配置模型，并用动态规划算法进行求解[5]；Huang等在企业产能无限、单源采购的环境下，研究了面向平台产品的产品族供应链优化配置问题，并运用遗传进行求解[6]；Graves等研究了保证服务模型下产能受限的多级供应链库存问题，并将单级库存模型扩展到多级供应链库存模型[7]；Qu等分别研究了供应链在具有装配结构、可选择供应商节点和网络结构这三种情况的优化配置问题，并运用分布式的多学科的优化算法目标级联分析法进行求解[8-10]；聂笃宪和屈挺等在多源采购环境下，对可选供应商引入采购比例调控因子，将服务时间和供应商实际采购比例作为决策变量，同时，建立了多级制造型供应链的优化配置数学模型，并采用改进的遗传算法进行求解[11]；Amin等在企业产能无限，单源采购的环境下，研究新产品在扩散效应下的供应链优化配置问题，并建立了供应链利润最大化的配置模型[12]；Li等考虑多源采购策略的情况下，新产品发布在扩散效应作用下的供应链优化配置问题，同时建立了最大化供应链总体利润的配置模型[13]；雷涛等研究了供应链内企业产能有限的情况下多级装配型供应链优化配置问题，并提出一种改进的遗传算法进行求解[14]。

综上所述，上述文献分为两类。第一类包括制造资源约束、采购策略的供应链配置的研究。这些研究通常只考虑单个产品的供应链，而不涉及基于产品平台的产品族供应链的概念。第二类包括有关产品平台概念和供应链性能的研究。这些研究考虑的是企业产能无限、单源采购的环境下进行产品平台与供应链的配置。但是在实际的生产过程中，企业的产能在一定时间内因人力、设备等资源的因素是有限制的。同时，在供应链风险管理方面，面对动态变化的市场环境（如顾客需求的不确定性等），采用单源采购使得供应链网络愈加脆弱，导致制造商更容易遭遇原材料及零部件供应中断的风险。为了应对供应链存在的这些不确定性，同时提高供应链的鲁棒性，越来越多的企业选择多源采购策略。本文将研究企业产能有限，在多源采购的环境下，基于产品平台的产品族供应链优化配置问题。建立一个基于产品平台的通用型产品族供应链网络优化数学模型，并提出一种基于自适应交叉与变异概率的改进遗传算法求解，最后研究产品平台的共性对供应链整体配置的影响。

1 问题描述与模型建立

1.1 问题描述。本文面向一个制造商用户已经确定的通用产品结构或通用物料清单设计和生产一组平台产品满足各种各样的市场需求，其可以选择不同的生产策略，如自制或外包。供应商负责提供各种各样的原材料给制造商。提供同种原料的可替代供应商拥有不同的生产能力和单位生产价格。在这个背景下，在最终产品需求到来之前，同时进行供应链和平台产品的配置决策。

如图1所示，圆形表示产品、制造商和供应商三种类型实体，其中P表示产品，M表示总装配制造商，SM表示平台组件制造商，S表示供应商，形成采购层（R）、装配层（P）和配送层（D ）。总装配制造商根据市场需求从供应商和平台组件制造商多源采购零件和平台组件生产n种产品组成的产品族，并根据自身产能情况将生产任务外包给其他总装配制造商。平台组件制造商根据总装配制造商的需求生产装配平台组件并从供应商多源采购原材料。供应商给总装配制造商和平台组件制造商提供原材料。根据上述将产品族供应链的运作模型转变为可配置的产品族供应链配置模型（如图2所示）。因此本文研究的产品族供应链配置问题为：在企业产能有限，采用多源采购的策略下，研究选择哪些总装配制造商进行外包，哪些平台组件制造商和供应商进行采购，同时设置各节点的采购比例和服务时间，在保证服务模式下，使产品族供应链的总配置成本最小。

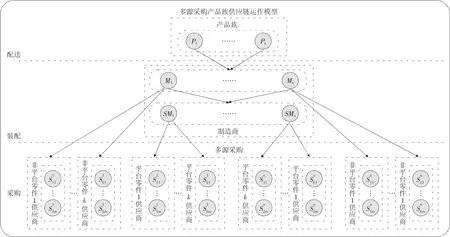
图1 产品族供应链的运作概念图

2 产品族供应链优化模型建立

2.1 参数符号含义及相关假设。其主要参数符号和相关含义如表1所示：

在建立配置模型前，作出如下假设：（1）供应链各节点采用定期盘点的基本库存策略，并为下游企业提供一个特定时间内到货的保证服务时间；（2） 假设在每个i∈E的需求阶段，产品的市场需求Zi服从N（ μi, σi）的正态分布。则在i∈R∪P（采的正态分布；（3）供应链每个节点以预定的服务水平满足下游节点的需求；（4）不考虑采购节点的上游节点，则采购节点的相邻上游供应商的服务时间和累计产品成本都为0；（5）D层节点的订单检查购和装配阶段），服从周期等于订货周期；（6）上游供应商单位累计成本为其采购价格，多源采购同一零部件为其平均值，且每个节点备选供应商不超过3个。

图2 产品族供应链的配置模型图

表1 相关参数符号和含义

2.2 模型建立。根据文献[6]，本文在企业产能有限，多源采购的环境下考虑包括安全库存成本、周转库存成本、在制品库存成本及主营业务成本（包含产品生产费、采购费和运输费用）的供应链总成本。

在不考虑可选供应商选项决策的情况下，由文献[6]，可得产能有限下每个选择模式的安全库存计算公式为：

其中：τi为供应链节点i的净补货时间，计算公式为：

NLBi和NUBi分别表示安全库存量与τi呈线性相关时，τi的下界和上界。其计算公式如下：

每个选择模式下的需求和方差为：

每个节点的累计成本为：

每个选择模式下成品累计成本价值：

总安全库存费用为：

每个选择模式下在制品累计成本价值：

每个选择模式下在制品库存为：

总在制品库存费用为：

周转库存为正常时段内的销售备货量。考虑到客户的需求应该在配送层D的节点得到及时满足，而采购层R和装配层P则是直接在每个订单周期末尾获取下游企业节点在这个周期的订单需求，因此除了配送层D的企业节点外其他企业层节点的ti都为0，参考文献[6]，则总的周转库存成本为：

参考文献[6]，主营业务成本为：

根据公式（1）～公式（13），则产能有限下采用多源采购策略的产品族供应链总成本配置模型为：

目标函数包括4个部分，前3个部分为每个阶段的库存成本之和，第4个部分为供应链的主营业务成本；约束式（14）表示供应链网络节点的需求分配，即对于每一个节点，下游企业节点总是将该原材料（零部件）的总需求按照采购比例xiOi分配给该节点的可选供应商；约束式（15）表示实际采购比例xiOi不能超过1；约束式（16） 为供应商最大产能约束大于对供应商的需求；约束式（17）确保服务时间为整数且非负数。

3 基于改进遗传算法的模型求解

3.1 染色体编码。采用实数与整数混合的基因编码方式。避免算法在运算过程中不停地进行编码操作和解码操作，从而减少

了算法求解的复杂性。对应编码如下所示：

3.2 适应度函数的设计。遗传算法中适应度函数的选取直接影响其收敛速度和能否找到最优解，一般目标函数即为遗传算法的适应度函数。本文选择基于排序的适应度分配函数，种群通过模型计算出目标函数值后，从小到大将函数值进行排序。染色体个体的序位即为该个体在种群的适应值。本文采用基于线性排序的适应度排序，因其在染色体排序中引入了种群的均匀尺度，为控制压力提供了相对简单且有效的方法，使其表现出更强的鲁棒性[15]。

3.3 选择策略。选择是为了把优化的染色体个体直接遗传到下一代。本文采用精英法与随机遍历抽样法相结合的方法。在计算好每个个体的适应度后，根据适应度的好坏将染色体进行排序，然后精英策略会将当代种群中适应度最好的染色体完整的保留到下一代新的种群中，剩下的染色体个体则使用随机遍历抽样法进行选择。

3.4 交叉策略。交叉是将两个染色体中的部分基因片段进行互换。本文采用具有自适应交叉概率pc[16-17]的单点交叉策略，该策略优点在于染色体适应度趋向一致或趋向局部最优时，增加交叉概率；而当其适应度偏向分散时，减少交叉概率。其自适应交叉概率pc计算如下：

其中：fmin表示种群中最小的适应值，favg表示种群中的平均适应值，f表示要进行交叉的两个染色体中较小的适应值，pc1,pc2为常数。

3.5 变异策略。变异是指子代的基因按照小概率扰动所产生的变化。本文采用具有自适应变异概率pm的变异策略，该策略优点在于染色体适应度趋向一致或趋向局部最优时，增加变异概率；而当其适应度偏向分散时，减少变异概率。其自适应交叉概率pm计算如下：

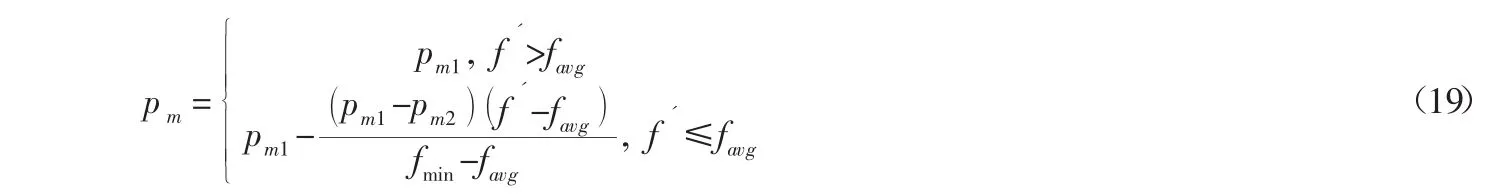
其中：f′为要变异染色体个体的适应度，pm1,pm2为常数。

3.6 修复策略。算法运行过程中，在经过交叉和变异操作之后，可能产生不符合约束条件的染色体，这些染色体需要被修复。产生的这些染色体有可能不符合约束式（14）。对应的修复策略是将不符合该约束条件的染色体基因段需要根据约束条件重新生成该染色体基因段的编码值。

4 实验仿真与分析

本文以文献[6]的笔记本装配供应链系统作为实例来验证模型的准确性及算法的可行性，供应链结构如图3所示，其中椭圆形表示零部件采购、部件/成品装配和成品配送这三种类型的节点。图3中的产品族供应链（Generic Supply Chain，GSC）以产品平台节点10为节点，可分解为两条实例供应链 （Instance Supply Chain，ISC），记为 ISCA（包含节点 NA=｛1,2,3,4,5,6,7,8,9,10,11,13,15,16｝） 和ISCB（包含节点NA=｛1,2,3,4,5,6,7,8,9,10,12,14,17｝）。表2和表3分别为供应链相关节点数据和市场需求的分布参数。

图3 笔记本装配供应链结构

假设供应链服务水平为98%，单位产品库存持有率为0.4，供应链节点年运作天数为300天，外部库存盘点时间。改进遗传算法参数种群规模为1 000，最大迭代次数为100，选择压力取2，精英个体为1，杂交率取0.7，变异率为杂交率除以染色体长度，本文仿真软件使用Matlab 8.4进行仿真模拟，其配置结果和收敛曲线如表4和图4所示。

从图4可以看出遗传算法在80代左右达到收敛，同时，表4的配置结果中可以看到每个有多备选选项的节点的选项1的采购比例占0.5～0.6之间，且这些选项的直接生产成本都相对较低，但服务时间比其他选项长。这说明在多源采购环境下，企业会向优先采购直接生产成本低的供应商，但会以增长供货时间为代价。

表5是通用供应链GSC与其分解的两条供应链ISCA和ISCB的配置费用。可以看到GSC（$1 976 201）网络的安全库存费用由于产品平台共性的作用大大低于ISCA+ISCB（$2 163 266）的安全库存费用，降低了9.74%。而同样由于产品平台共性的作用GSC（$172 638 929） 网络供应链总成本比ISCA+ISCB（$172 887 901） 的供应链总成本显著减少了$248 972。因此，产品平台共性对安全库存成本的降低有显著的影响，对供应链总成本的降低有显著的影响。

表2 相关节点数据

表3 市场需求的分布参数

表4 优化配置结果

5 结论

本文解决了多源采购和产能有限的产品族供应链优化配置问题，以实际采购比例和交货期为决策变量建立一个基于产品平台的产品族供应链优化模型，并提出自适应交叉与变异概率的改进遗传算法进行求解。最后通过实例笔记本装配供应链网络验证了优化数学模型的准确性和算法的有效性。同时得出产品平台共性对安全库存成本的降低有显著的影响，对供应链总成本的降低有显著的影响。

表5 配置费用

本文为市场需求波动，企业产能受限，面向多源采购策略的产品族供应链优化问题提供了一种有效的数学模型，同时给出了相应的优化方法。未来还可以对产品族供应链产品结构不确定的供应链配置问题继续研究。

图4 模型收敛曲线

参考文献：

[1]Li Z,Pehlken A,Qian H,et al.A systematic adaptable platform architecture design methodology for early product development[J].Journal of Engineering Design,2016,27(1-3):93-117.

[2]Gerchak Y,Henig M.Component commonality in assemble-to-order systems:Models and properties[J].Naval Research Logistics,2015,36(1):61-68.

[3]Kristianto Y,Helo P,Takala J.Strategic inventory allocation for product platform strategy[J].Journal of Advances in Management Research,2017,7(2):233-249.

[4]Chiu S,Kuo J S,Chiu V,et al.Cost Minimization for a Multi-Product Fabrication-Distribution Problem with Commonality[J].Postponement,and Quality Assurance,2016,21(3):38.

[5]Graves S C,Willems S P.Optimizing the Supply Chain Configuration for New Products[M].INFORMS,2005.

[6]Huang G Q,Zhang X Y,Liang L.Towards integrated optimal configuration of platform products,manufacturing processes,and supply chains[J].Journal of Operations Management,2005,23(3-4):267-290.

[7]Graves S C,Schoenmeyr T.Strategic Safety-Stock Placement in Supply Chains with Capacity Constraints[J].Manufacturing&Service Operations Management,2016,18(3):445-460.

[8]Ting Qu,George Q.Huang,Van-Dat Cung,et al.Optimal configuration of assembly supply chains using analytical target cascading[J].International Journal of Production Research,2010,48(23):6883-6907.

[9]Huang G Q,Qu T.Extending analytical target cascading for optimal configuration of supply chains with alternative autonomous suppliers[J].International Journal of Production Economics,2008,115(1):39-54.

[10]Qu T,Huang G,Chen X,et al.Extending analytical target cascading for optimal supply chain network configuration of a product family[J].International Journal of Computer Integrated Manufacturing,2009,22(11):1012-1023.

[11]聂笃宪，屈挺，陈新,等.面向多源采购的多级供应链优化配置方法[J].工业工程，2014(4):54-62.

[12]Amini M,Li H.Supply chain configuration for diffusion of new products:An integrated optimization approach[J].Omega,2011,39(3):313-322.

[13]Haitao Li,Mehdi Amini.A hybrid optimisation approach to configure a supply chain for new product diffusion:a case study of multiple-sourcing strategy[J].International Journal of Production Research,2012,50(11):3152-3171.

[14]雷涛，屈挺，聂笃宪,等.产能约束下的多级装配供应链优化配置方法研究[J].工业工程，2014(5):93-98.

[15]连松友，姜国利，余云鹏,等.蓝光过滤多层功能薄膜的遗传算法设计[J].表面技术，2017,46(8):170-175.

[16]Park C H,Lee W I,Han W S,et al.Improved genetic algorithm for multidisciplinary optimization of composite laminates[J].Computers&Structures,2008,86(19-20):1894-1903.

[17]Zhao J,Fan X,Sun Q.Stacking sequence optimization of composite laminates for maximum buckling load using permutation search algorithm[J].Composite Structures,2015(121):225-236.