两阶段神经网络算法预测物流联络中心任务量

0 引言

联络中心（Contact Center）作为语音交换和通讯产业的应用分支之一，是以信息技术为依托、以多渠道通讯为手段实现交互式实时通讯和及时沟通的全网融合平台[1-3]。

目前，学者对联络中心任务量进行预测的方法主要有时间序列方法[4-5]，其中包括移动平均方法、指数平滑法、ARMA模型、支持向量机、kalman滤波等。学者在智能算法方面也有了许多研究，例如神经网络[6]、粒子群算法[7]等。利用BP神经网络进行预测的优点是可以模仿人脑的智能化处理过程，在对非精确性规律问题的处理上具有较强的自适应能力。如何适应时代发展，精准地预测联络中心的任务量，成为人们需要进行深入研究的热点问题。

本文提取物流联络中心任务量数据，提出一种两阶段神经网络算法预测模型对联络中心的任务量进行预测。本算法（MIPSO-BP）分为两个阶段，第一阶段利用MIV算法优化BP神经网络的输入变量和利用动态惯性权重调整方式与局部极值调整策略相结合的改进粒子群优化算法（IPSO）优化BP神经网络的初始权值和阈值；第二阶段进行BP神经网络训练和预测。数值实验表明，本文的改进方法有助于提高BP神经网络的预测精度。

1 两阶段神经网络预测模型

1.1 粒子群优化算法的改进

1.1.1 惯性权重的更新

本文的惯性权重根据粒子的目标函数值进行动态调整的同时，还考虑迭代关系。惯性权重调整公式如下：

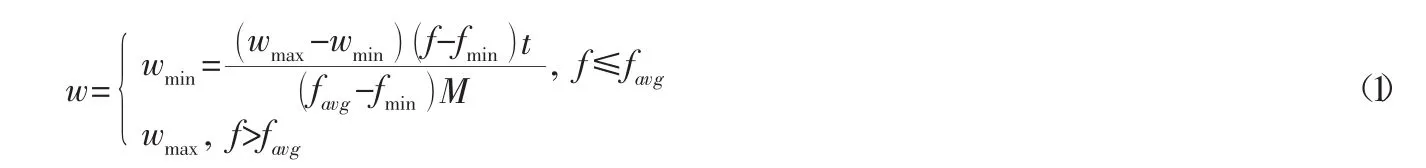
其中：f表示粒子当前的目标函数值，favg和fmin分别表示当前所有微粒的平均目标函数值和最小目标函数值，wmax和wmin分别表示w的最大值和最小值。t和M分别表示当前迭代次数和最大迭代次数。

公式（1）中，若微粒的目标函数值比平均目标函数值小，通过减小惯性权重，来增强局部搜索能力；反之，若微粒的目标函数值比平均目标函数值大，通过增大惯性权重，来增强全局搜索能力，让粒子向更好的搜索区域靠近。

1.1.2 局部极值的调整

本文参考文献[7]的改进策略，即判断通过相邻2次最优适应度函数值之差小于某个值时，则认定粒子可能陷入局部极值，并重新随机初始化粒子群的位置，该判断方式存在片面性。由于一次借助相邻值判定已陷入局部极值可能导致一些进展顺利的位置被放弃而导致重复运行的情况发生，从而加大了工作量。因此需在迭代过程中加大判断次数，即若相邻m（ 3≤m≤ ）5次最优适应度函数值之差小于某个值ε时，就认定该粒子可能已经陷入局部极值，记录当前获取的全局最优粒子的位置信息，重新随机初始化粒子群的位置，继续进行迭代，反复进行此过程，直至迭代结束。

本文改进惯性权重的粒子群算法参数设置如下：学习因子c1和c2均取值为2，惯性权重w根据公式（1）更新。目标函数为BP神经网络误差，即公式（2）：

1.2 第一阶段：BP神经网络的优化处理

1.2.1 BP神经网络输入变量的优化处理

采用大量与输出无关数据作为神经网络输入可能导致神经网络在训练期间产生错误和在预测阶段产生较大的预测误差的问题。因此，本文采用平均影响值（Mean Impact Value,MIV）算法筛选出对预测日任务量影响较大的输入数据，这样的处理使得预测模型在简化BP神经网络结构的同时有利于提高神经网络的预测精度。

1.2.2 BP神经网络初始权值和阈值的优化处理

BP神经网络的训练对初始权值和阈值十分敏感。若选取不当，会影响网络的预测精度。通过引入动态惯性权重调整方式与局部极值调整策略相结合的改进粒子群优化算法来获取BP神经网络的初始权值和阈值，能够使初始权值和阈值更加贴近实际问题的权值和阈值，让BP神经网络的训练过程更加精准，从而提高神经网络预测的精确度。

（1）建立一个三层的BP神经网络预测模型

首先，输入层，根据MIV算法筛选后的变量所对应的任务量数据作为神经网络的输入。依据输入变量的个数可以确定输入层神经元个数。

其次，隐含层，根据试凑法（在编程中试出使误差最小的隐含层神经元个数）确定隐含层神经元的个数。

最后，输出层，神经网络的输出对应某时间点的任务量，输出层神经元个数根据输出变量来确定。

将输入和输出数据利用公式（3）进行归一化处理到［0,1］范围内。

（2）设置粒子群自变量个数

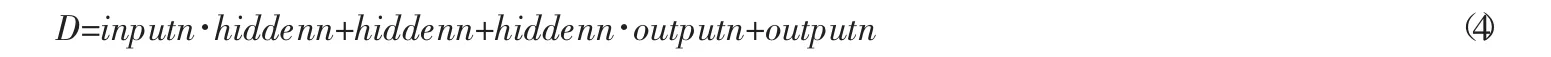
其中，inputn、hiddenn、outputn分别为BP神经网络的输入层、隐含层、输出层神经元个数。

通过改进惯性权重的粒子群算法来求得目标函数的最优值，然后将最优值赋给BP神经网络的初始权值和阈值。

1.3 第二阶段：BP神经网络的训练和预测

1.3.1 BP神经网络的训练

首先，把通过本文改进粒子群算法获得的BP神经网络的初始权值和阈值赋值给神经网络。

其次，设置网络参数。包括隐含层和输出层的传递函数，网络学习函数、迭代次数、目标误差等。

最后，对网络进行训练。

1.3.2 BP神经网络的预测

输入新的数据，利用训练好的BP神经网络进行预测，获得预测结果。

2 实例分析

2.1 数据分析

本文采用某物流联络中心的2016年12月份的任务量数据。该物流联络中心任务量数据如图1所示。

图1统计出12月份，按照周一至周日划分的每半小时相同时间段的任务量平均值。由图1可以看出，工作日任务量数据呈现明显的日周期性，尽管每天的任务量数据呈现相似的发展趋势，但是每天的任务量到达模式不同，因此周一至周五对应5个不同的预测模型，有利于更好地反映不同天的任务量特征，同时可以简化BP神经网络的结构。

周六和周日任务量数据和工作日的任务量数据有着明显的差别，为了准确地预测周末的任务量数据，应将周六和周日看成两个不同的预测模型，同时不同于工作日。

图1 12月份每天每半小时采样点的任务量数据

2.2 物流联络中心任务量预测

通过对某物流联络中心2016年12月份任务量的历史数据进行分析，首先从定性的角度，选出表1中的10个输入变量，可能对预测日的任务量有较大的影响；然后从定量的角度，通过MIV算法对表1中的10个变量进行筛选，表1是通过MIV算法计算的数值结果（工作日）。

表1 各输入变量的MIV值

由表1可以看出，输入变量5,8,9的MIV值的绝对值相较于其他输入变量，绝对值很小，这说明5,8,9三个输入变量对输出变量的影响十分小，因此为了简化BP神经网络的拓扑结构，可以直接剔除5,8,9的输入变量。

采集某物流联络中心12月份每一天上午7:45到晚上23:45的每15min时间间隔的任务量数据，以12月2日（周五），12月9日（周五），12月14日（周三），12月15日（周四） 每天15min时间间隔的任务量数据作为BP神经网络的输入，以12月16日（周五）的每15min时间间隔的任务量数据作为BP神经网络的目标输出，建立一个包含输入层、隐含层、输出层的三层BP神经网络。其中输入层、隐含层和输出层神经元个数分别为7,9,1；

隐含层和输出层的传递函数分别为‘tansig’和‘logsig’；学习函数为‘trainlm’，最大迭代次数为5 000，目标误差设为104。利用matlab对本文建立的BP神经网络进行训练，并采用以下三种模型进行预测：

第一种，MIPSO-BP表示本文提出的两阶段神经网络算法预测模型，学习因子c1和c2均取值为2，m取5，惯性权重w为改进的惯性权重公式（1）；

第二种，IPSO-BP表示文献[6]改进粒子群算法优化BP神经网络的预测模型，学习因子c1和c2均取值为2，ε取值为0.7，惯性权重按梯度调整；

第三种，BP表示使用单一BP神经网络的预测模型。

运用训练好的神经网络模型预测12月23日（周五）每15min时间间隔的任务量。实际值与预测值得结果如图2所示：

图2 工作日BP神经网络预测结果对比

由图2可以看出，IPSO-BP预测模型和单一BP神经网络预测模型的预测值与实际值的误差较大，而MIPSO-BP预测模型的预测值与真实数据有相似的发展趋势，MIPSO-BP预测值与真实数据之间的误差最小。

由于周末任务量到达模式比较特殊，周末BP神经网络的预测模型采用预测时刻前三个时刻的数据作为输入变量，目标输出为第四个时刻的任务量，这种处理参考其他BP神经网络预测问题。周六运用7:00～16:00每15min时间间隔的36个数据进行训练，周日采用17:00～23:30每15min时间间隔的26个数据进行训练，分别采用BP神经网络、IPSO-BP神经网络和MIPSOBP神经网络进行预测。

为了更加直观地判断本文提出的两阶段神经网络算法预测模型的任务量预测精准度，分别采用平均绝对误差MAE，平均平方误差MSE，平均百分比平方误差MSPE，平均绝对百分比误差MAPE这四个评价指标对本文预测模型进行评价。

其中：为第i时刻的任务量预测值，yi为第i时刻的任务量实际值。

表2 工作日不同预测模型评价结果对比分析

以上四个评价指标值越小说明预测值与实际值之间的差距越小，预测结果更加精确，模型的有效性越强。由表2可以看出，本文提出的预测模型MIPSO-BP的四个评价指标值均比单一BP神经网络的预测模型以及IPSO-BP预测模型的评价指标值小，说明本文提出的两阶段神经网络算法预测模型具有较好的预测效果。由表3可以看出，预测模型评价指标结果与工作日相比，工作日的评价指标值均优于周末。其中，周六的平均百分比平方误差MSPE，平均绝对百分比误差MAPE数值均超过100%，说明预测模型的误差十分大。因此，本文提出的两阶段神经网络算法预测模型更适合工作日任务量的预测。

3 结束语

本文在MIV算法筛选的基础上，通过动态惯性权重调整方式与局部极值调整策略相结合的改进粒子群优化算法来求得最优值，将其赋给BP神经网络的初始权值和阈值，并建立联络中心的任务量预测模型，充分利用了BP神经网络良好的非线性逼近能力，准确地拟合出了联络中心任务量数据的特征，该模型对联络中心的任务量进行了更加准确的预测，具有一定的实际应用价值。

表3 周六、周日不同预测模型结果对比分析

参考文献：

[1]李军祥，戴韬，叶春明.云计算下的分布式联络中心服务设计[J].上海理工大学学报（自然科学版），2014,36(4):328-334.

[2]王晓娜，李军祥.基于多技能多渠道变成本的物流联络中心排班[J].运筹与管理，2017,26(8):81-85.

[3]H Shen,J Z Huang.Interday Forecasting and Intraday Updating of Call Center Arrivals[J].Manufacturing&Service Operations Management,2011,10(3):391-410.

[4]Deven K.Barrow.Forecasting intraday call arrivals using the seasonal moving average method[J].Journal of Business Research,2016,69(12):6088-6096.

[5]R Ibrahim,H Ye,P L'Ecuyer,et al.Modeling and forecasting call center arrivals:A literature survey and a case study[J].International Journal of Forecasting,2016,32(3):865-874.

[6]ME Jalal,M Hosseini,S Karlsson.Forecasting incoming call volumes in call centers with recurrent Neural Networks[J].Journal of Business Research,2016,69(11):4811-4814.

[7]方群，徐青.基于改进粒子群算法的无人机三维航迹规划[J].西北工业大学学报，2017,35(1):66-73.