大型高铁站实名制验票旅客到达与服务规律研究

高铁车站是高速铁路系统中重要的基础设施，是客流集散的场所。大型的高铁进站通道内依次设置人工售（取）票窗口、自动售（取）票机、实名制验证闸机、安检机器、自动检票闸机和人工检票口等服务设施设备。实名制验票是高速铁路车站旅客进站必经的通道，也是旅客进站服务的重要环节。研究实名制验票的旅客到达和服务规律，对利用排队论或仿真方法研究该系统的设置、开放数量和布局具有重要意义。在轨道交通服务设施旅客到达和服务规律方面，学者们通常关注人工售（取）票窗口、自动售（取）票机、安检机器和检票闸机的研究[1]，对大型高铁站实名制验票系统旅客到达和服务规律的可靠研究几乎是空白。本文通过对实名制验票系统旅客到达和服务规律的探究，对进一步研究大型高铁站实名制验票系统的设备数量配置及布局、系统仿真，或对涉及实名制验票系统的其他研究均具有重要价值。

1 实名制验票旅客到达与服务分析

1.1 旅客进站流程

乘坐高铁的旅客从其他交通方式衔接进入高铁车站后直至乘车，通常需要经过取购票、实名制验票、安检和检票进站4个环节，不需要在站购买或取出车票的旅客需经过实名制验票、安检和检票进站3个环节，旅客进站流程如图1所示。高铁站内实名制验票系统是旅客进站的必经通道，是高铁站内付费区与非付费区的分界。乘坐高铁的旅客有买票、取票以及选择人工服务或自动售（取）票机服务的差别，安检环节旅客完成实名制验票后快速聚集，而检票闸机和人工检票口是候车旅客在可检票时段内聚集到达检票区排队。而本文所研究的实名制验票环节，其旅客到达特征与取购票、安检、检票3个环节有所差别，在服务上由于流程的差别也有所不同。

1.2 实名制验票旅客到达与服务过程

实名制验票系统旅客到达通常会受高铁枢纽的旅客到达的影响，高铁枢纽的旅客到达具有随机性和波动性。一般来说大型高铁车站旅客到达会受到高铁站列车发往方向、发车时间、车站所在城市经济社会发展水平、居民出行习惯等因素的影响，不同的高铁枢纽乘客到达呈现出不同的规律，则实名制验票系统旅客到达规律也不同。

图1 高铁站旅客进站流程示意图

实名制验票的服务流程明确，服务时间较为稳定，服务时间与旅客年龄、出行经验、教育水平、操作熟练程度相关，机器的识别效率、正确率和故障率也影响实名制验票的服务时间。

2 实名制验票旅客到达时间间隔与服务时间的统计拟合

2.1 数据调查统计

2.1.1 最少统计次数的确定

假设进行N次独立试验，统计得随机变数X的平均值为mx，均方差为σx，随机变数的小于给定的ε的概率为P则实名制验票与安检系统旅客到达时间间隔和服务时间的数据最少统计数据量N，可以由下式确定：

式（1） 中Q为置信水平，φ-1为拉普拉斯的反函数[6]。

若假设σx≈0.1，置信水平Q=0.95，ε=0.01，通过查拉普拉斯函数表可知，N=384。即实名制验票系统旅客到达时间间隔和服务时间的数据最少统计量应为384组数据。

2.1.2 数据调查

根据长沙南站历史数据，清明节、劳动节和国庆节假期为年旅客发送量高峰，13:00～18:00为日高峰时段。如图2所示的2017年4月1日长沙南站旅客发送量变化，该日共计发送112 986人次，属于全年高峰时期。如图3所示，长沙南站日旅客进站在8:00～9:00和13:00～15:00时出现高峰，旅客进站人数日低谷出现在10:00左右。为保证精度和调查的可操作性，本文选择调研时间为2017年3月22日至4月1日的13:00～18:00，对长沙南站西站房实名制验票旅客排队进行调研，采用现场视频记录，经回放后进行人工记录而获得原始数据，统计出实名制验票旅客到达时间间隔有效数据447个和服务时间有效数据500个，数据统计结果如表1所示。

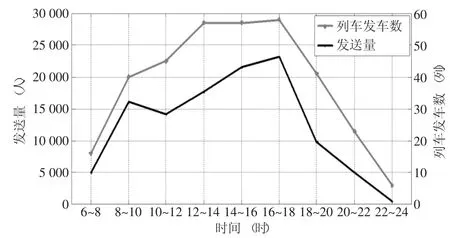
图2 2017年4月1日长沙南站客流量和列车发车数变化图

图3 长沙南站旅客日进站人数变化图

表1 实名制验票旅客到达时间间隔和服务时间统计

2.1.3 数据随机性检验

为了确保调查数据是随机序列，本文采用SPSS软件对到达时间间隔和服务时间数据进行单样本随机性检验，其中，原假设为：小于等于均值和大于均值所对应的数据序列是随机序列，设定置信度为α=0.05，置信水平为0.95。检验结果为：实名制验票到达时间间隔统计显著性为0.092，实名制验票服务时间统计显著性为0.134，数据显著性均大于显著性水平0.05，说明调查数据为随机序列，可以对实名制验票到达时间间隔和服务时间数据进行统计分布的拟合。

2.2 数据拟合

2.2.1 事件流的理论分布

统计的数据分组并计算频率，生成频率分布直方图，用事件流的理论分布曲线进行数据拟合。在排队论和可靠性理论中，常见分布有：二项分布，泊松分布，负指数分布，爱尔朗分布，正态分布等。根据文献[2]，事件流分布的拟合效果易受到实际数据变异系数的影响，其中指数分布只在数据变异系数为1附近的情形下拟合效果较好，变异系数远离1时，拟合效果下降，正态分布拟合效果一般，在变异系数较小时拟合效果较好，变异系数稍大时，拟合效果会变得十分差。因此，设实名制验票旅客到达时间间隔或服务时间为t，则可根据数据的变异系数vt，采用合适的统计分布对旅客到达时间间隔和服务时间数据进行拟合，讨论是否符合正态分布 （vt＞0 ），负指数分布（vt=1 ）或k阶爱尔朗分布（0＜vt＜1 ）（实名制验票旅客到达时间间隔和服务时间分布为连续型概率分布，而泊松分布为离散型概率分布，因此不作考虑）。其中k阶爱尔朗分布的函数为：

k阶爱尔朗分布函数包含2个参数，即阶数k和λ，其中阶数k可由数据的变异系数vt通过式子作初步确定，当k=1时，k阶爱尔朗分布即为负指数分布。若实名制验票旅客到达时间间隔或服务时间t服从k阶爱尔朗分布，则有

2.2.2 最小二乘法拟合

常见的事件流理论分布概率密度函数为非线性，本文采用非线性最小二乘法进行数据拟合。假设有一组数据xi，yi且已知这组数据满足某一函数原型其中为待定参数向量，则最小二乘法曲线拟合的目标就是求出这一组待定参数的值，使得目标函数式（3）最小：

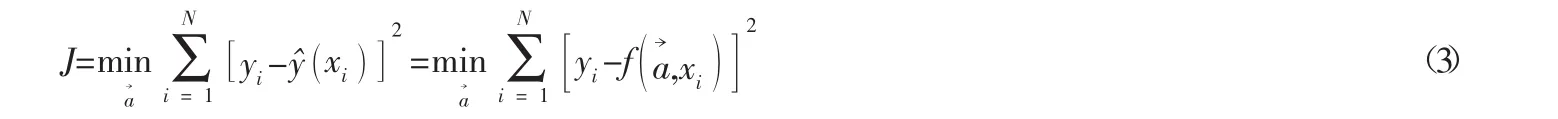
在Matlab软件中利用lsqcurvefit函数可对数据作非线性最小二乘拟合并求解出拟合函数的参数向量a→。

由表1，实名制验票旅客到达时间间隔和服务数据变异系数均小于1，计算出用k阶爱尔朗分布拟合实名制验票旅客到达时间间隔和服务时间数据的阶数k值，分别为1.21,2.16，因此可用2阶爱尔朗分布和3阶爱尔朗分布对数据进行拟合。用Matlab软件对实名制验票旅客到达时间间隔和服务时间数据做出频率直方图，并分别用负指数分布、2阶爱尔朗分布、3阶爱尔朗分布、正态分布4种分布的概率密度曲线进行最小二乘拟合。如图4所示，（a）～（d）分别为实名制验票到达时间间隔的4种分布拟合曲线图，图5（a）～（d）分别为实名制验票服务时间的4种分布拟合曲线图。

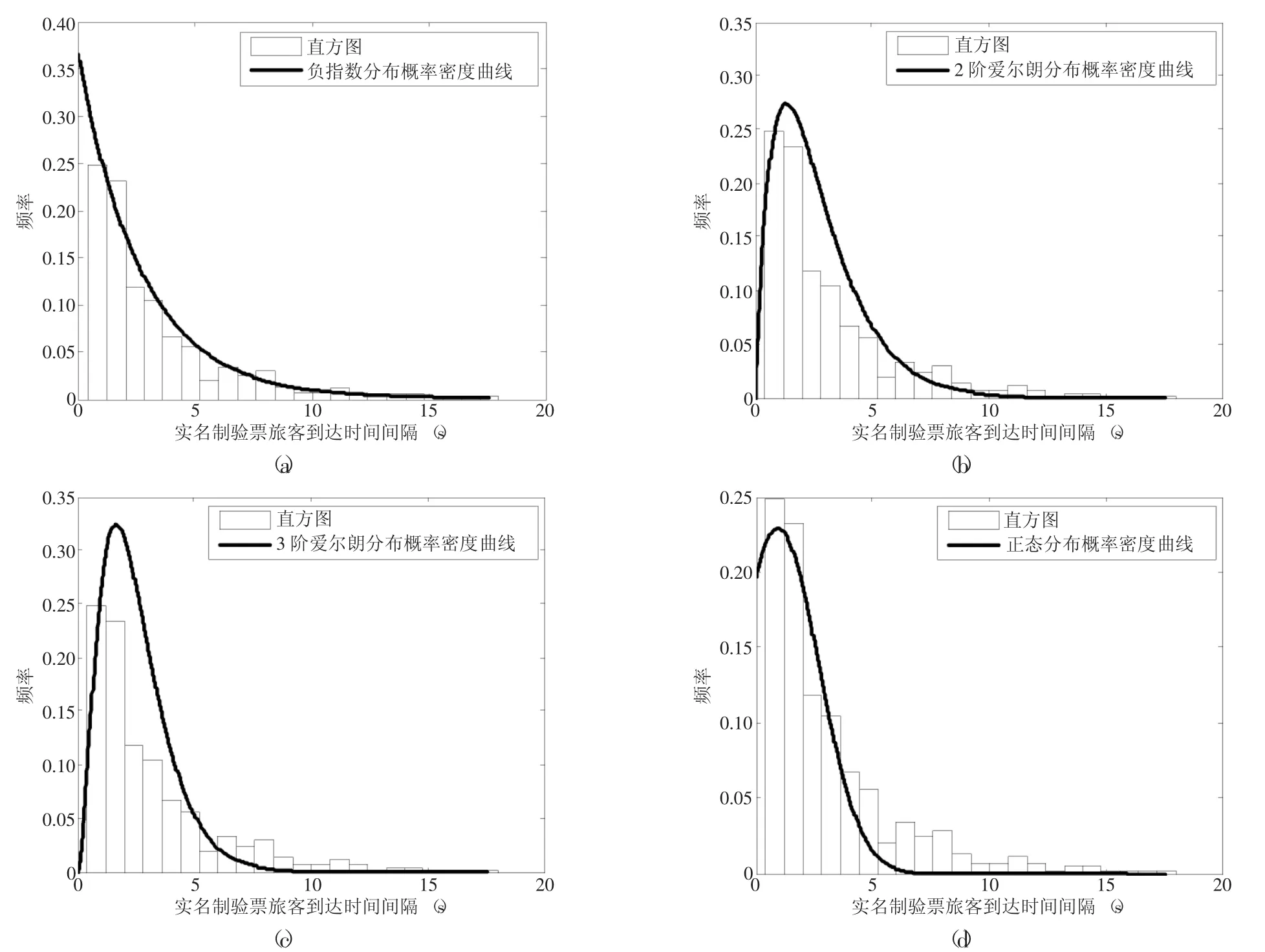
图4 实名制验票旅客到达时间间隔分布拟合曲线图

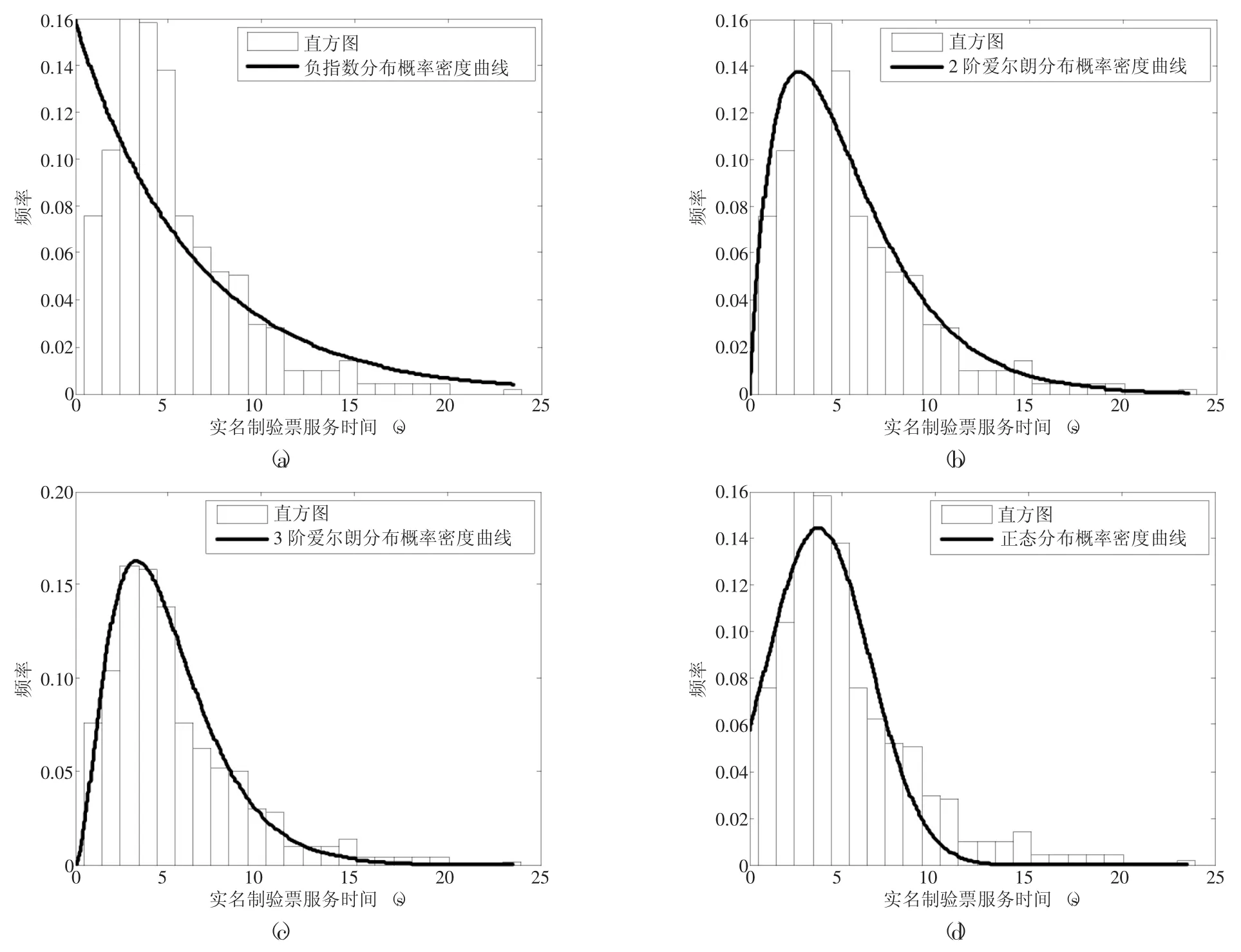
图5 实名制验票服务时间分布拟合曲线图

观察图4可知，实名制验票到达时间间隔在3s以下的旅客较多，4种分布对实名制验票旅客到达规律的拟合较好，而由图5，实名制验票的服务时间多集中在4s～5s左右，依次往两端递减，2阶爱尔朗分布、3阶爱尔朗分布和正态分布对实名制验票的服务时间规律拟合较好。拟合的效果需要进一步作适度检验。

3 旅客到达和服务规律的检验

设旅客到达时间间隔和服务时间统计分布Fn（x）服从理论分布F（x），为检验这个假设是否成立，采用皮尔逊卡方检验法进行适度检验。假设H0:Fn（x）=F（x ）；H1:Fn（x）≠F（x）。计算卡方统计量：

式中k为分组数目，mi为第i组统计频数，pi为第i组理论频率，n为样本量。给定置信度为α=0.05，自由度R=k-s-1，其中s为估计参数的数目，由χ2分布表求出卡方临界值

如果则拒绝H0，即认为总体的分布不服从假设H0中的分布；若则接受H0，即认为总体的分布服从F（）x分布。

对实名制验票旅客到达时间间隔和服务时间数据的分布曲线，运用皮尔逊卡方检验，结果如表2至表3所示。

表2 实名制验票旅客到达时间间隔分布形态检验表

由表2和表3，正态分布和3阶爱尔朗分布不能描述实名制验票旅客到达时间间隔和服务时间分布规律。实名制验票旅客到达时间间隔服从负指数分布，其概率密度函数为：

表3 实名制验票服务时间分布形态检验表

实名制验票服务时间服从2阶爱尔朗分布，其概率密度函数为：

长沙南站实名制验票系统由多个服务台构成，一个服务台可同时服务1名旅客，旅客先到先服务，旅客源可以视为无限制。根据实际情况，实名制验票过程为多路排队多通道服务，可视为多个单通道服务，则可以确定实名制验票服务系统为多台M/E2/1/∞/∞/FCFS的并联排队模型。通过回放调查视频，记录实名制验票系统每名旅客完成服务时队列的等待队长数据和系统队长数据各150个，每名旅客排队等待时间数据和在系统逗留时间数据各150个。经统计，实名制验票各服务台旅客平均到达率为9.2人/min，平均服务时间5.37s，计算实名制验票系统运行指标与实际观测的平均值对比进行检验，对比结果如表4所示。

表4 实名制验票系统运行指标检验结果

根据计算，实名制验票系统运行指标误差均不超过10%，符合实际情况，说明统计分布具有较高的准确性。

4 结论

（1）通过对长沙南站的实名制验票到达时间间隔与服务时间的调查、统计拟合，得到大型高铁站实名制验票旅客到达时间间隔服从负指数分布，服务时间服从2阶爱尔朗分布。

（2）利用实名制验票旅客到达和服务规律对系统运行指标进行计算，计算结果误差小于10%，得到的统计分布准确性高。

（3）经检验后的实名制验票旅客到达和服务规律可靠，可用于大型高铁站实名制验票系统的仿真，以及用于大型高铁站实名制验票系统服务台的数量配置、开放数量及布局等方面的研究，具有较高的应用价值。

参考文献：

[1]乔庆杰.高速铁路中小型车站安检仪和检票闸机布局研究[D].北京：北京交通大学（硕士学位论文），2010.

[2]胡路，蒲云，蒋阳升,等.城市轨道交通车站到达客流时间间隔分布拟合[J].系统工程理论与实践，2014,34(7):1835-1846.

[3]周侃.高铁客运枢纽换乘行为分析与设施配置方法研究[D].哈尔滨：哈尔滨工业大学（博士学位论文），2013.

[4]姜耀武.高速铁路车站售票及安检设备数量配置研究[D].长沙：中南大学（硕士学位论文），2013:26-27,43-44.

[5]刘明姝，张国宝.基于排队系统的城市轨道交通进站检票机配置[J].城市轨道交通研究，2004,7(5):34-37.

[6]张晓东.大庆西站客流组织与客运设施配置仿真分析[D].大连：大连交通大学（硕士学位论文），2015.

[7]陆凤山.排队论及其应用[M].长沙：湖南科技出版社，1994:122-125.

[8]蒋淑华，伏小良.基于排队论的超市收费服务模型的探讨[J].物流科技，2008(10):141-142.

[9]王健，胡碧琴.基于排队论的港口泊位服务系统优化仿真研究[J].物流科技，2011(7):31-35.

[10]孙继东.城市轨道交通车站乘客服务设施客流到达分布规律研究[D].成都：西南交通大学（硕士学位论文），2014.