基于多天线的星间GPS高精度相对定位方法
艾 奇 王 向 武 静 卢 翔 张国柱
1.上海航天控制技术研究所,上海201109 2. 上海市空间智能控制技术重点实验室,上海 201109
星间相对定位是卫星编队、空间交会对接、在轨维护及抓捕的关键技术,传统的星间相对测量手段如光学成像系统、激光雷达及微波雷达等,在测量范围、测量距离及测量精度上都有一定的局限性,且都必须保持视线指向控制,航天器在轨运行的能源主要来源于太阳能帆板,由于结构限制、空间遮挡等原因导致某些特殊功能航天器视线指向过程中无法保证帆板对日,不利于航天器在轨任务的开展[1]。基于GPS(Global positioning system)的星间相对测量技术对于航天器在轨姿态指向要求不高,且其全天候、全空域、测量距离大、范围广、测量设备体积小和无极性要求等诸多优点在空间应用领域体现了巨大的优势。
在过去几十年的空间科学应用中,尤其是空间交会对接方面,星间相对定位成为远、近程交会段及近程机动段(5km~200m)的主要导航手段,但由于多径效应及信号遮挡等影响在超近程不能采用星间相对定位。随着航天技术的不断发展和空间任务的复杂性增大,空间操控、交会对接等任务中航天器无法保证GPS天线指天,且不断的轨道机动使得基于精密轨道动力学模型定轨的卡尔曼滤波算法和基于GPS双频双差处理技术的载波相位差分无法连续输出。针对上述问题,本文提出了一种基于多天线的星间GPS载波相位差分技术,可以实现毫米级精度的超近程相对导航。
1 星间GNSS相对定位技术
GNSS(Global Navigation Satellite System)泛指所有卫星导航定位系统,包括美国的GPS、俄罗斯的GLONASS、中国的北斗系统(Compass)及欧盟的GALELIO等,目前GPS系统应用最为普遍。以GPS系统为例,一个GPS用户在全球范围内通常可以获得优于10m(95%)的定位精度和20ns(95%)的授时精度,然而这对于航天器的超近程高精度导航要求还远远不够,因此需要用到增强GPS技术即差分GPS(DGPS)系统。DGPS系统按照解算方法可分为基码技术和基于载波的技术;基码GPS系统主要依赖于GPS码(即伪距)测量值,而基于载波的DGPS系统则主要依赖于载波相位测量值。DGPS系统能提高航天器绝对定位精度的根本原因在于利用目标航天器和自身的原始测量数据(伪距或载波相位),通过适当处理确保两组观测数据相对于GPS系统时间调整到一个共同测量时基上形成双差(DD),最终可以抵消GPS接收机和卫星时钟的偏差及大部分的大气层传播延迟。区别在于载波相位测量值要比伪距测量值精确得多,继而能达到毫米级的相对定位水平[2]。
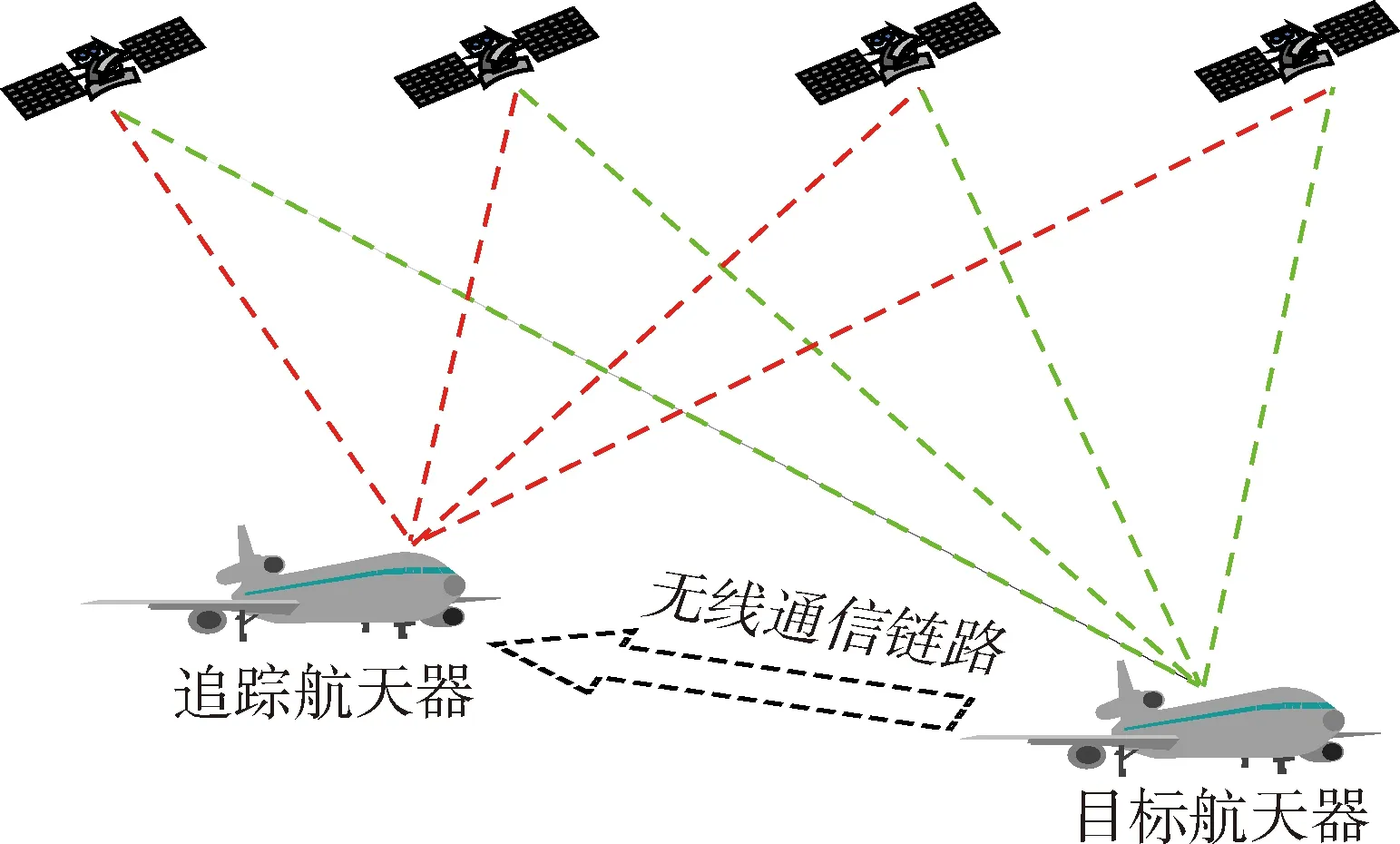
图1 星间GNSS相对定位示意图
星间GNSS相对定位基本结构如图1所示,根据星间观测方程得知,同一导航系统(如GPS系统)间形成星间相对定位至少需要5颗共视导航星,且其结果准确来说是2个航天器接收天线的相位中心之间的相对位置,由于超近程导航处理中不能将航天器视为点目标,且对于毫米级高精度相对定位不能忽略在轨时天线相位中心稳定度造成的误差(约2mm)[3]。故需要考虑GPS天线相位中心到航天器质心(也可以是任意一点,本文以质心为例)的折算及折算过程中姿态测量误差带来的转换误差影响。
2 观测量质心归算
利用GPS观测值进行航天器定轨或者相对导航,本质上是要确定航天器质心的位置或者相对位置。解决这个问题的方法之一就是在进行定位解算之前将每个GPS天线的观测量归算到航天器质心处,这一过程需要综合利用航天器的姿态信息。图2是伪距/载波观测量质心归算示意图。
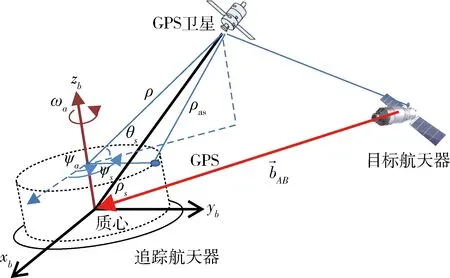
图2 GPS观测量质心归算示意图
如图2所示,设GPS天线安装位置距离目标航天器质心的距离为ra,某一时刻某GPS卫星的方位角为ψs,高度角为θs(在地固系ECEF下计算得到),GPS天线测得的相位中心到该GPS卫星的距离是ρ,归算到质心后的测距量是ρs。则ρs在地固系ECEF下的投影以及标量形式可以分别表示为:
(1)
(2)
式中,下标B代表本体坐标系;(ra)B为ra在本体系下的投影;航天器姿态定义为绕本体轴按照ψ→θ→φ(轴的旋转顺序为3→2→1)的顺序旋转到ECEF;A为绕本体轴的旋转矩阵;c和s分别表示cos和sin。以欧拉角形式给出上式中的方向余弦矩阵如下:
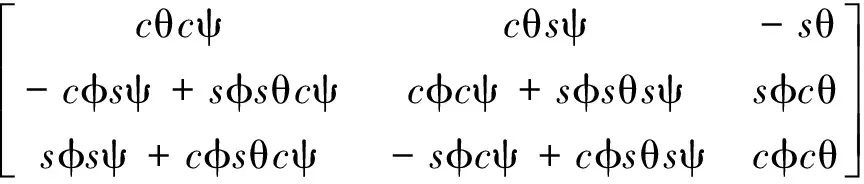
(3)
按照式(1)将GPS天线相位中心处的测距观测值换算到航天器质心以后,可以再进行差分相对导航。
3 相对定位精度分析
3.1 姿态误差影响
利用航天器的三轴姿态信息,可以将GPS卫星到航天器上GPS天线的观测量归算成GPS卫星到航天器质心。图3是观测量质心归算示意图。

图3 观测量质心归算示意图
如图3所示,假设GPS天线安装在距离航天器质心ra处,某一时刻某GPS卫星的方位角为ψs,高度角为θs,GPS天线测得的相位中心到该GPS卫星的距离是ρas(即代表载波相位或者伪距观测值),且记归算到质心后的测距量是ρs。
为研究姿态确定误差对质心归算的影响,利用误差传递规律可以计算由姿态角误差引起的接收机测距量归化误差为
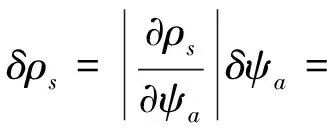
(4)
式(4)表明姿态角误差造成的观测数据质心归算误差除了与天线姿态角误差δψa有关以外,还与天线的安装位置、GPS卫星的方位角和高度角等因素有关。
假设ra=2m,ψa0=0按照不同接收方位角、高度角,姿态角误差造成的观测数据质心归算误差如图4。
可以看出,在姿态角误差约1°的条件下,造成的高仰角卫星(≥45°)的观测数据质心归算误差小于1cm;但是如果接收仰角比较低(<20°)时,1°的姿态角误差将有可能造成约2cm的质心归算误差。这一误差基本与电离层残差相当。由于控制系统姿态测量误差一般在0.2°以内,可以得到质心归算误差在0.2×2cm=4mm以内,比电离层残差相比小了一个数量级,因此对最终结果的影响不起决定性作用,对最终的计算结果影响可忽略。
3.2 相对导航解算方法

利用差分GPS技术进行航天器相对导航有动力学和运动学2种方法。由于本文涉及的航天器存在频繁轨道机动和姿态控制,故采用后者。运动法相对导航的最大特点就是不受卫星动力学模型的影响,因此结果较稳定,其精度主要由伪距和载波相位测量的精度决定。主要步骤包括4步,如图5所示。

图5 运动学相对导航方法流程图
1)构建载波相位双差观测方程
首先用2台接收机分别安置在基线的2个端点,对2个端点的接收机进行单点定位,作差获得相对位置的伪距解:
rAB0=rA0-rB0
(5)
确定2个接收机同时观测的导航星,计算载波相位双差观测残值,构建精确载波相位双差观测方程。
2)数据质量控制
对双差观测数据进行野值剔除、周跳检测与修复、随机模型精化、观测方程病态性检验与正则化等操作。
3)模糊度固定
根据整周模糊度产生的原理可知,整周模糊度的真实值应该是确定的整数。求解整数模糊度的一般思路是:在获得了模糊度浮点解之后,利用其方差-协方差在浮点解附近建立一个的搜索区域;再在该区域内搜索出一些候选整数解;最后根据一定的判据从候选解中选出最终的模糊度整数解[5]。基于整周模糊度的浮点解及其方差-协方差矩阵,本文使用目前被公认为最优的整数最小二乘方法LAMBDA( Least-Squares Ambiguity Decorrelation Adjustment)来搜索整数解。
4)相对位置解算
消去了模糊度的双差载波相位可以视作一种更高精度的伪距测量,能显著提高相对位置解的精度。因此在确定了载波相位模糊度N之后,可以利用消去模糊度的双差载波相位观测量求解相对位置修正矢量δrAB,获得准确的相对位置矢量rAB。
rAB=rA0-rB0+δrAB
(6)
4 外场实验验证及精度评估
外场试验在空旷平地中放置一台三轴转台,转台由伺服电机驱动,按编程设定的角速率旋转;各轴均安装有编码器,能实时测量转台相对于初始时刻的转动角度。2个GPS天线(A和B)对称安装于转台上,随平台一起绕转台竖直轴顺时针旋转,转速设定为40(°)/s,另一台接收机及天线O静置安装在远处三角架上,2台接收机的实时观测数据通过无线链路传输至PC机保存并进行事后处理,如图6所示。

图6 外场实验图
首先使用双差载波相位确定了平台转动天线A相对于静置的GPS天线O的位置矢量方向,如图7截取了其中600s的数据示意。

图7 OA基线位置矢量(前600s数据)
按照编码器测得的转台旋转角度,将A、B天线的观测数据归算到C点,再利用双差载波相位计算OC基线矢量。与此同时,利用已经计算得到的OA和OB基线矢量,可以计算OC基线矢量的参考值:OC=(OA+OB)/2。将观测数据归算后计算得到的OC基线矢量与参考值进行比较,可以获得如图8所示的OC基线相对定位误差,统计结果如表1。

图8 OC基线相对定位误差
实时观测数据通过无线链路传输至PC机保存并进行事后处理,如图6所示。

表1 OC基线相对定位误差统计
5 结论
星间高精度相对定位是航天器相对导航的重要手段,本文提出了一种基于多天线的星间GPS高精度相对定位方法并完成地面实测验证,毫米级相对定位精度对于具有复杂空间任务的航天器具有很好的应用前景。
参 考 文 献
[1] 梁志国,巨涛.GPS相对定位在星间测量中的应用[J].航天器工程, 2010, 19(1): 94-98.(Liang Zhiguo,Ju Tao. Research on Application of GPS Relative Position in Inter-Satellite Measurement [J],Spacecraft Engineering,2010, 19(1): 94-98.)
[2] 梁昆淼. GPS技术与应用[M]. 2版. 北京:高等教育出版社,1978.
[3] Elliott D.Kaplan,Christopher Hegarty. GPS原理与应用(第二版)[M]. 2版. 北京:电子工业出版社,2007.
[4] Remco Kroes, Oliver Montenbruck,William Bertiger,Pieter Visser.Precise GRACE Baseline Determination Using GPS[J]. GPS Solutions, 2005, 9 (1): 21-31.
[5] P. J. G. Teunissen.The Least-squares Ambiguity Decorrelation Adjustment: Its Performance on Short GPS Baselines and Short Observation Spans[J].Journal of Geodesy, 1997, 71 (10): 589-602.

