INS/GNSS紧组合导航系统故障探测与隔离的改进研究
邵梦晗 熊寸平 程 风 高晓颖
1.北京航天自动控制研究所,北京 100854 2.宇航智能控制技术国家级重点实验室,北京 100854 3.武汉大学卫星导航定位技术研究中心,武汉 430079
INS/GNSS组合导航是提高导航精度的一种常用手段,已在工程中广泛使用。按照组合方式的不同,分为松组合、紧组合和深组合。目前,基于位置和速度的松组合导航系统已经相当成熟,它因计算量小、实现容易而在民用、军用领域都得到广泛使用。但是松组合也有不可避免的缺陷:GNSS提供的用于组合的信息是经过内部解算得到的位置、速度信息,它们是时间相关的,导致滤波的稳定性较差;并且必须要求可见星数目不少于4颗。松组合本质是将GNSS接收机与可见星的相对位置信息转换为地理坐标系下的位置信息,然后与惯性导航的结果作差构成观测值;紧组合则是直接利用GNSS原始观测值:伪距和伪距率,将惯性导航解算的地理坐标系下的位置信息转换为与可见星之间的相对距离信息,再与GNSS提供的伪距和伪距率作差构成组合导航的观测值。因此,紧组合能够在松组合不可用的条件下使用,尤其是当可见星数目少于4颗的情况下依然能进行,从而提高组合导航系统的可靠性和精度。
容错组合导航系统是目前组合导航系统的发展方向之一,这些系统具有故障检测、诊断、隔离和系统重构的功能[1]。在设计的容错方案中,对于以惯性导航为主体的组合导航系统,一般采用冗余惯性传感器的结构来提高惯性导航系统的可靠性。因此,GNSS组合导航系统的故障判断准则是:若系统INS/GNSS故障,则判定导航系统GNSS故障[1]。INS/GNSS系统故障探测的关键是对GNSS提供的信息的正确性判别。在紧组合中主要是对GNSS接收机提供的伪距和伪距率进行质量检测。目前的容错算法设计都是基于整个组合系统,对INS/GNSS滤波后的新息或结果误差进行检验[2-4],该方法必须在组合卡尔曼滤波计算后进行,一定程度上浪费了大量的时间和内存。针对于此,基于INS/GNSS故障判断准则,本文提出一种容错INS/GNSS紧组合结构:在进行组合导航滤波计算前,先单独对GNSS系统进行故障星检测,即伪距和伪距率可信性检测,隔离故障星,确定可靠的伪距、伪距率观测值组合后,再联合INS进行卡尔曼滤波解算,得到准确的定位结果。
容错设计的核心是进行系统自监控,实时地故障检测与隔离(Fault Detection and Isolation, FDI)。一旦检测到故障就必须对故障进行隔离,最后通过系统信息重构使整体不致因故障而失效。目前,广泛采用的一种故障探测方法是基于数理统计的χ2检验法,它是利用对卡尔曼滤波器的新息构造统计检验量,进行二元假设检验。文献[4]提出一种残差χ2检验法与双状态χ2检验法并行工作且共用一个卡尔曼滤波器的方法,有效解决了单一χ2检验法的缺陷,该方法仅能实时确定一组观测值的有效性,不能确定故障的发生位置和具体原因。本文在传统χ2检验法的基础上,将w-检测法与χ2检验法结合进行故障探测与定位,并通过实测数据仿真,验证了探测的精确性。确定故障星后,对其伪距和伪距率信息进行剔除,利用剩余的卫星信息进行系统重构,能有效提高系统的可靠性和完备性。
1 INS/GNSS紧组合故障检测与隔离结构设计
本文提出的INS/GNSS紧组合导航系统的故障探测结构设计如图1所示。
在传统的紧组合导航系统中,添加了故障星探测、识别与剔除模块,具体过程是:首先对GNSS原始伪距、伪距率观测信息进行故障探测,识别和剔除掉故障卫星,得到正确的伪距、伪距率观测信息,然后再与INS组合,进行卡尔曼滤波解算。采取这样的算法,对GNSS原始观测值可靠性进行预判断,能够有效保证后续滤波计算结果可靠。同时,结构简单,系统耦合影响较小,能准确确定GNSS引起的故障位置,隔离错误观测信息。
2 改进故障探测检验法原理与应用
2.1 w-检测法与χ2检验法结合的故障识别算法
传统的残差χ2检验法只能用来确定INS/GNSS系统某一历元的观测值中是否存在粗差,即是否存在故障星,若存在,则直接将这一历元的全部观测值进行隔离,单独利用惯性导航的机械编排结果作为紧组合系统的输出。这样必然会使这一时段的导航精度下降,相当于牺牲结果精度来确保可靠性。文献[5]则提出一种基于层次滤波器结构的故障检测与系统重构方法,主滤波器利用所有卫星的观测信息,子滤波器分别弃用1~n号卫星的量测信息,然后对子滤波器的χ2检验,当只有1个子滤波器未检测到故障时,就可判断该子滤波器弃用的卫星即为故障星。该方法结构复杂,运算量大。针对于此,本文采用w-检测法与χ2检验法结合的方法,在已知单位权方差,观测值互相独立的情况下,先利用χ2检验法进行观测值有效性的判断,对确定存在故障星的历元,再进行w-检测,识别故障星并予以剔除,剩余正确的GNSS伪距、伪距率组合进入INS/GNSS紧组合卡尔曼滤波计算中,具体流程如图2所示。

图2 w-检测法与χ2检验法结合的故障探测流程
该方法在组合卡尔曼滤波前进行,只针对GNSS原始观测值进行粗差的探测和剔除。因此,对于伪距、伪距率错误,这种做法是可行的,而且能在前端就对观测信息做筛选,大大提高后续组合导航结果的收敛性和可靠性。
2.2 改进的最小二乘残差检测法
GNSS伪距观测方程为:
ρi=|rsi-rR|+ctR+εi
(1)
式中,ρi是伪距观测值;|rsi-rR|是接收机与第i颗卫星的几何距离;ctR是接收机钟差在距离上的投影;εi是观测误差,包括卫星钟差、大气延迟误差等。观测值的最小二乘残差为:
V=Bx-L=-(I-B(BTD-1B)-1BTD-1)L
(2)
令残差向量的精度(改正数的协因数矩阵):
DV=D-B(BTD-1B)-1BT
(3)
所以式(3)可以写为:
V=-(DVD-1)L=-(DVD-1)ε
(4)
令S=DVD-1,S称为敏感矩阵,反映了观测误差ε对残差改正数的影响程度。观测误差通过敏感矩阵映射到残差上,因此,可以通过检测残差来判断观测值中是否有粗差存在。设原假设H0:当前观测值中不存在粗差;备选假设H1:当前观测值中有粗差。无论采用何种平差方法,残差平方和服从自由度为n-u、非中心化参数为δ的χ2分布[6]:
(5)
在一定的误警概率α下,有检测门限值:
(6)
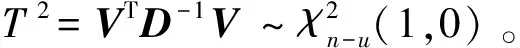
以χ2检验法确定存在故障卫星的历元后,利用w-检测法进行粗差定位,分别计算该历元每个观测值的wi[7]:
(7)
其中,σvi是DV对角线上的元素,sii是敏感矩阵S对角线上的元素,σi是观测值Li的中误差,σvi是对应的残差中误差。实际上,wi就是标准化的残差,在原假设成立的条件下,wi服从标准正态分布,即wi~N(0,1);否则wi服从非中心化参数为δi的正态分布:wi~N(δi,1)。
在一定的误警概率α下,有检测门限值:
K=N1-α/2(0,1)
(8)
其中,N1-α/2(0,1)为在给定的置信度1-α下的临界值。若|wi|≤K,则以1-α的概率认为观测值Li没有粗差,接受H0;反之,若|wi|≥K,则拒绝原假设,推测Li含有粗差,予以剔除。
2.3 改进的新息检测法
把w-检测法与χ2检验法结合用到卡尔曼滤波解算里,只是把最小二乘的残差平方和转换成新息平方和。与最小二乘不同的是,当前时刻的故障输出将影响预测值,使它“跟踪”故障输出,因此故障存在后效性,在故障消失后容易产生误警。
新息是当前历元k时刻的观测值与预测值的差值,即预测残差:
Vk,k-1=Lk-Lk,k-1
(9)
仿照改进的最小二乘残差法,先利用新息平方和服从自由度为n-u、非中心化参数为δ的χ2分布:
(10)
确定存在故障的历元后,再结合w-检测法,把标准化的新息作为统计检验量。原假设H0为Vk,k-1~N(0,DVk,k-1),若k时刻的第i个观测值Li含有粗差▽bi(k),其新息为[8]:
Vk,k-1(bi(k))=Vk,k-1(i)-▽bi(k)
(11)
这时,备选假设H1为:
(12)
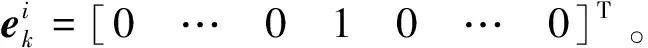
(13)
其中,
(14)
在给定的误警概率下,计算临界值N1-α/2(0,1)。若某一历元中最大的标准化新息超出临界值,则标记该观测值为错误观测值,将其剔除,重新利用剩余观测值进行滤波估计,构造假设检验统计量进行检验,直到剩余的新息全部通过检验。
3 仿真分析
3.1 仿真方案设计
仿真实验采用运动速度约为5m/s的GNSS伪距观测数据,观测卫星数10颗,GNSS接收机采样频率是2Hz,采集500s的观测数据,共1000个历元。对原始伪距观测值进行了大气误差改正、相对论改正等处理,通过仿真模拟3号卫星故障,即在3号卫星的伪距观测值中,加入不同形式的粗差模拟卫星故障,具体方法如下:按时间段分别添加绝对值为60m的阶跃故障(硬故障)、斜率为2m/s的慢变斜坡故障(软故障)以及斜率为4m/s的快变斜坡故障(软故障),仿真故障模式见表1。

表1 仿真故障模式设置
在INS/GNSS紧组合之前,对GNSS数据分别采用改进的最小二乘残差法(方法1)和改进的新息检测法(方法2)对故障星探测,设置误警率α=5%,自由度是5(可见卫星数减去必要卫星数),则χ2检验法的检测门限为Td=11.0705,w-检测法的检测门限为Nd=1.6449。比较改进检测算法在两种应用场景下的区别。
3.2 仿真结果与分析
3.2.1 改进的最小二乘残差检测法
将w-检测法与χ2检验法结合后运用到最小二乘中,在故障1、故障2和故障3三种模式下,得到结果如图3~5所示。
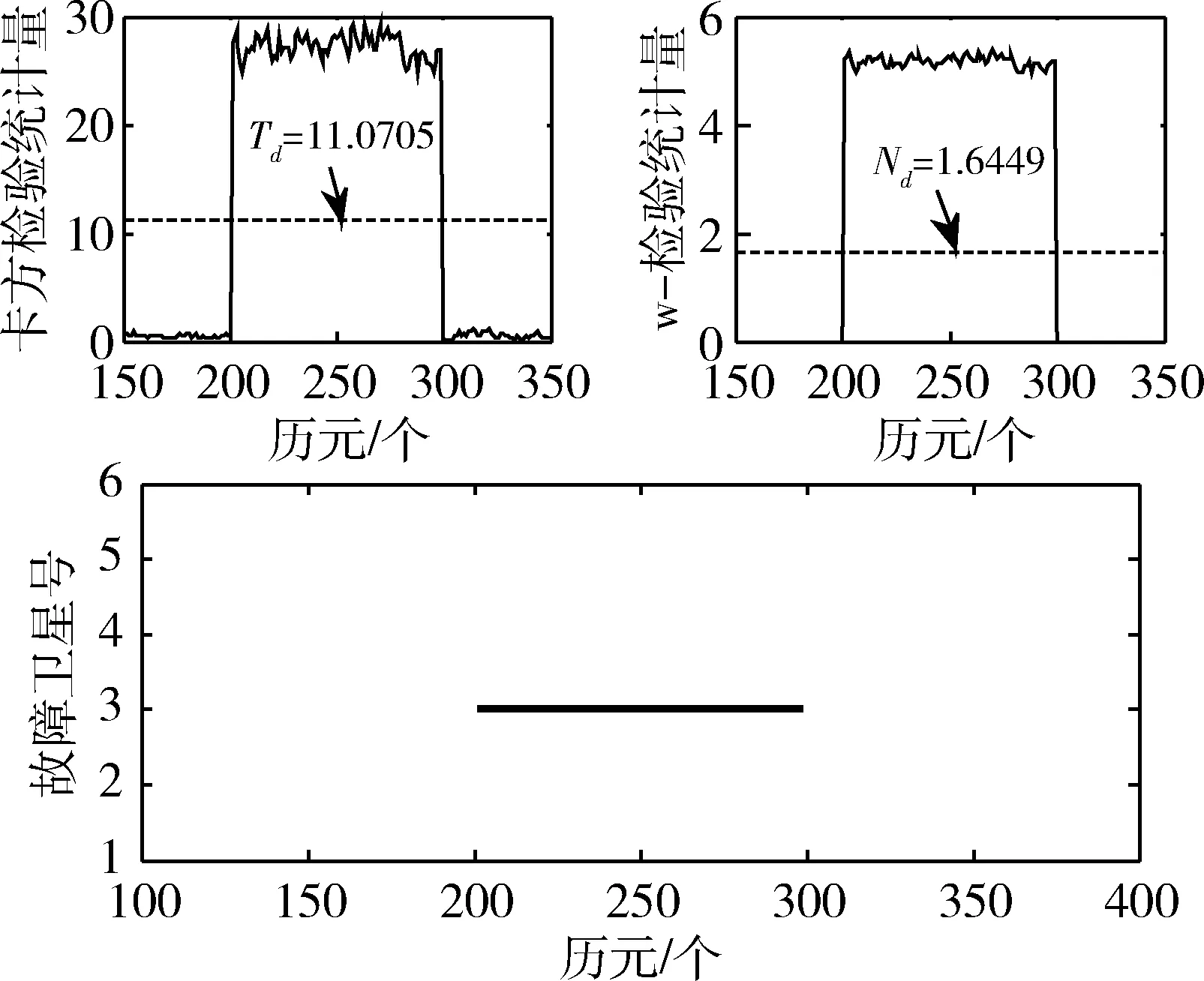
图3 故障1模式下方法1故障识别结果
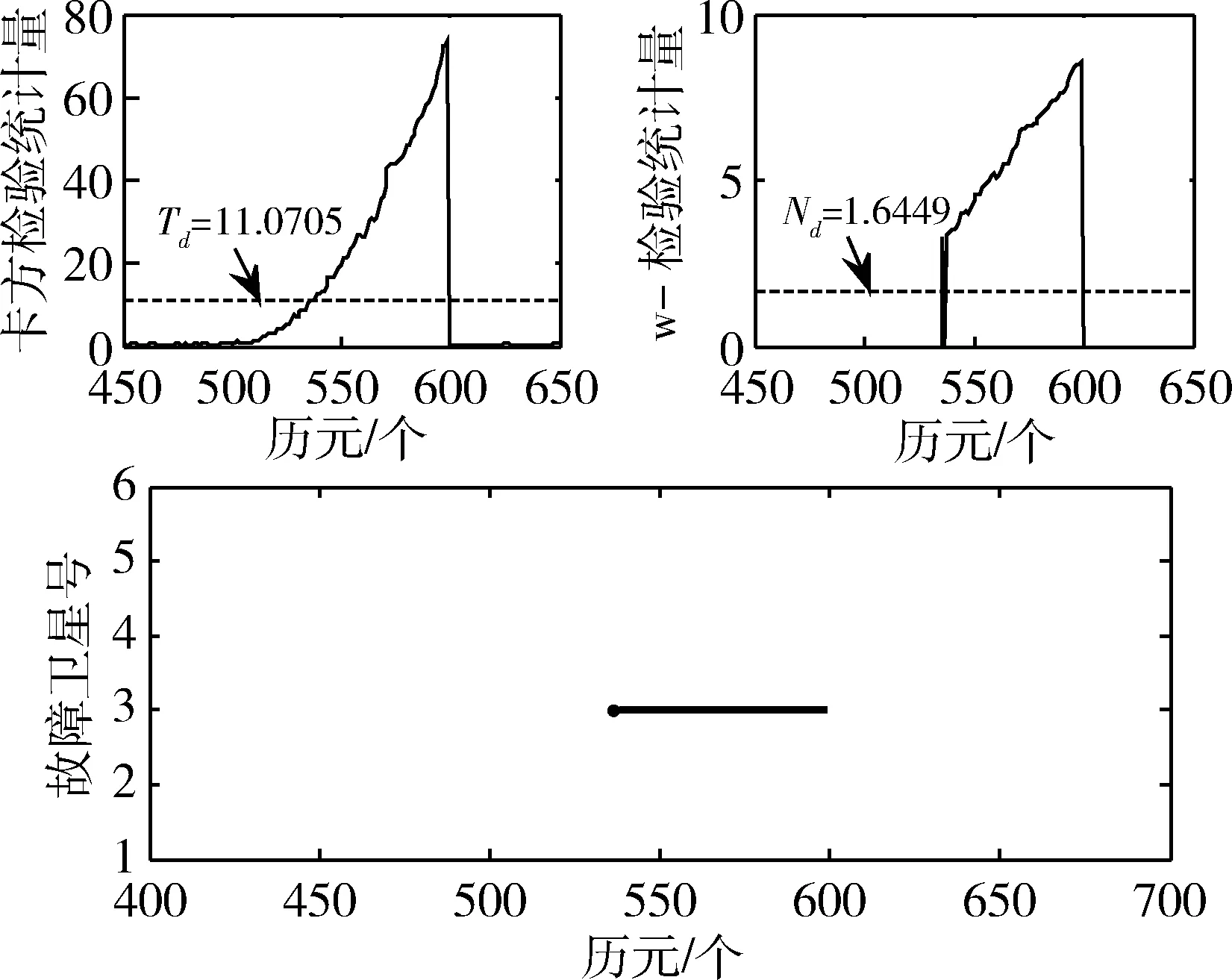
图4 故障2模式下方法1故障识别结果
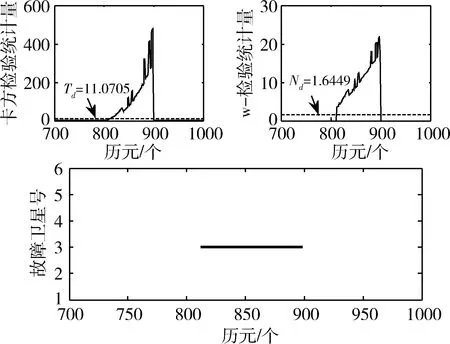
图5 故障3模式下方法1故障识别结果
由图3~5可以看出,无论何种故障模式,将w-检测法与χ2检验法结合后运用到最小二乘中,都能精确地定位某一历元发生故障的卫星,进而可以在滤波前隔离错误伪距、伪距率,选择正确的原始观测值组合。对于60m较大的阶跃故障(图3),该方法能够迅速反应并探测到错误观测值;对于2m/s的慢变斜坡故障(图4),由于刚开始的粗差较小,残差χ2检验对其不够灵敏,未能检测出故障星,但当粗差增大到一定值,通过w-检测法能够正确识别故障星;对于4m/s的快变斜坡故障(图5),探测到软故障的累计时间明显缩短,反应更为迅速。
3.2.2 改进的新息检测法
将w-检测法与χ2检验法结合后运用到卡尔曼滤波中,在故障1、故障2和故障3三种模式下,结果如图6~8所示。

图6 故障1模式下方法2故障识别结果

图7 故障2模式下方法2故障识别结果
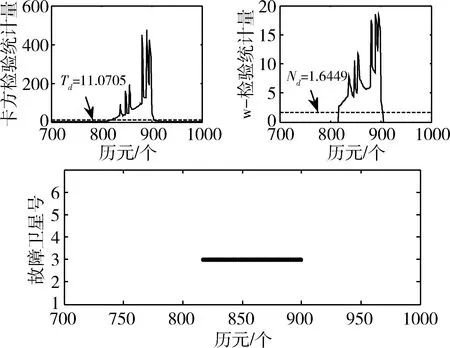
图8 故障3模式下方法2故障识别结果
由图6~8可以看出,在卡尔曼滤波中运用这种方法后,除了个别历元外,大部分历元能正确识别故障星。对于60m较大的阶跃故障(图6),200~250历元存在错误定位故障卫星号现象,误把6号卫星作为故障卫星;对于2m/s的慢变斜坡故障(图7),同样因残差χ2检验对软故障不够灵敏,当粗差增大到一定值,通过w-检测法能够正确识别故障星。与最小二乘不同的是,在故障消除段600历元以后,该方法仍显示有故障存在,存在误警,分析原因是因为当前时刻新息中受上一时刻的观测粗差影响,即故障存在后效性;对于4m/s的快变斜坡故障(图8),探测到软故障的累计时间明显缩短,反应更为迅速,误警仍存在但有所改进。
对比这2种应用场景,可以看出,由于卡尔曼滤波新息检测量受前一时刻故障的影响,使得残差χ2检验“跟踪”故障输出,对故障的反应时间有所延迟,且有一定的后效性。并且由于前后2个时刻滤波值存在相关性,通过w-检测法正确识别故障星的探测率是80.67%,正确率是86.36%。而在最小二乘中的残差检测量只受当前时刻故障的影响,该方法则无后效性;且通过w-检测法识别故障星的探测率达到83.33%,正确率达到100%。因此,相对于利用滤波后的新息构造检验量探测故障星,单纯的利用GNSS最小二乘残差构造检验量进行卫星故障识别结果更好。综上,无论是最小二乘还是卡尔曼滤波,综合运用w-检测和χ2检验的方法,取合适的显著性水平,均能正确识别、剔除故障星,选择可靠的观测值组合;但由于χ2检验本身的特点,对开始较小的软故障而言,反应不够灵敏,故障时间判断存在一定的延迟。
4 结论与展望
对于INS/GNSS紧组合容错系统的设计,目前大多数方法都是在组合滤波之后进行故障检测,且传统的残差χ2检验无法确定故障的具体原因和位置。针对卫星测量信息故障,本文提出在进行组合导航滤波计算之前,单独对GNSS系统进行伪距和伪距率可信性检测;并将w-检测法引入,在已知单位权方差,且观测值互相独立的情况下,先利用χ2检验法进行观测值有效性的判断,对确定存在故障星的历元,再进行w-检测,识别故障星并予以剔除,剩余正确的GNSS伪距、伪距率组合进入INS/GNSS紧组合卡尔曼滤波计算中。在最小二乘和卡尔曼滤波2种场景下运用改进算法,在合适的显著性水平下,均能正确识别故障星,选择可靠的观测值组合进入组合滤波阶段。但由于χ2检验本身的特点,对软故障而言,故障时间判断存在一定延迟,继而影响w-检验也存在延迟效应。对于这一问题,可以加入惯性导航系统信息或者其他辅助信息,增加冗余观测量,进行故障的探测与隔离。
参 考 文 献
[1] 秦永元, 张洪钺, 汪叔华. 卡尔曼滤波与组合导航原理 [M]. 第3版. 西安: 西北工业大学出版社, 2015.(Qin Yongyuan, Zhang Hongyue, Wang Shuhua. Kalman Filter and Integrated Navigation Principles [M]. The third edition. Xi′an:Press of Northwestern Polytechnical University, 2015.)
[2] 吴有龙, 王晓鸣, 杨玲, 等. 两级故障检测与隔离方法在组合导航中的应用分析[J]. 弹道学报, 2013, 25(4):53-58,64.(Wu Youlong, Wang Xiaoming, Yang Ling, et al. Dual-stages Fault Detection and Isolation Method for Integrated Navigation System [J]. Journal of Ballistics, 2013, 25(4):53-58,64.)
[3] 刘海颖, 岳亚洲, 杨毅钧, 等. 基于多解分离的GNSS/Inertial组合系统完好性监测[J].中国惯性技术学报, 2012, 20(1):63-68.(Liu Haiying, Yue Yazhou, Yang Yijun, et al, Integrity Monitoring for GNSS/Inertial Based on Multiple Solution Separation [J]. Journal of Chinese Inertial Technology, 2012, 20(1):63-68.)
[4] 张华强, 李东兴, 张国强. 混合χ2检测法在组合导航系统故障检测中的应用[J]. 中国惯性技术学报, 2016, 24(5):696-700.(Zhang Huaqiang, Li Dongxing, Zhang Guoqiang. Application of Hybrid Chi-square Test Method in Fault Detection of Integrated Navigation System [J]. Journal of Chinese Inertial Technology, 2016, 24(5):696-700.)
[5] 张闯, 赵修斌, 庞春雷, 等. GNSS/SINS紧组合导航故障检测与系统重构新方法[J]. 电光与控制, 2017, 24(2):100-104.(Zhang Chuang, Zhao Xiubin, Pang Chunlei, et al. A New Method of GNSS / SINS Tightly Integrated Navigation Fault Detection and System Reconstruction [J]. Electronics Optics & Control, 2017, 24(2):100-104.)
[6] 李德仁,袁修孝. 误差与可靠性理论[M]. 第二版. 武汉: 武汉大学出版社,2012.(Li Deren, Yuan Xiuxiao. Error Processing and Reliability Theory [M]. The second edition. Wuhan:Press of Wuhan University, 2012.)
[7] Baarda W A. Testing Procedure for Use in Geodetic Networks [R]. Publications in Geodesy, New Series, Netherlands Geodetic Commission, Delft, Netherlands, 1968.
[8] 吴云. GNSS粗差检测的“快照”法与“滤波”法的比较研究[J]. 武汉大学学报(信息科学版), 2010, 35(06):649-652,704.(Wu Yun. A Comparative Study of "Snapshot" and "Filtering" Methods for GNSS Error Detection [J]. Geomatics and Information Science of Wuhan University, 2010, 35(6):649-652,704.)
[9] Teunissen P J G. Quality Control in Integrated Navigation Systems [C]. IEEE Plans (90), Las Vegas, 1990.

