基于鲁棒自适应反步法的四轴平台稳定回路控制
王慎航 张焕鑫 杨 轶 许 琦 林瑞仕 杨名军
北京航天自动控制研究所,北京100854
三轴陀螺稳定平台[1-3]作为导航、制导与控制技术中的关键惯性测量设备,已经广泛应用于航天、航空和航海等领域。三轴陀螺稳定平台框架[4]的“失锁”现象导致它仅限用于机动姿态有限的载体上。若载体需要在全姿态状态下工作,就必须采用四轴结构。三框架四轴平台是在原来两框架三轴平台的基础上,增加了一个随动框架,即增加了一个自由度,以避免“失锁”现象。
三框架四轴平台[5-6]是一个多输入、多输出系统,包含了转动惯量耦合、摩擦力矩、惯性耦合力矩、外部干扰、模型参数未知及不确定性等各类因素,这些都将影响稳定回路控制的动态性能和静态性能。为了获得稳定回路良好的鲁棒性能和跟踪性能,国内外学者在平台稳定回路控制领域做了大量研究。PID[7-8]控制由于其控制算法简单、鲁棒性较好及易于实现等优点,广泛应用于平台稳定控制系统,但其对于系统干扰的抑制能力有限。干扰观测器[9-11]也越来越多的应用于稳定回路的补偿控制中,但这种算法的前提是系统的参数已知,但实际系统中总是存在参数未知和不确定性的情况。滑模变结构控制[12]由于对参数不确定性和干扰具有强抑制性能也被应用于稳定回路的控制中,但滑模变结构控制一般不可避免地存在“抖震”现象,将会导致系统的动态性能变差。还有其他一些方法,如:自抗扰控制[13]、H∞鲁棒控制[14]、自适应控制[15]和最优控制[16]等方法,这些方法大多没有考虑参数未知、不确定性或外部干扰的情况,不能保证系统良好的鲁棒和跟踪性能。
针对存在模型未知、不确定参数以及外界干扰项的平台系统稳定回路,提出了一种鲁棒自适应反步控制方法。
1 四轴稳定平台数学模型
1.1 坐标系定义及运动学分析
如图1所示,四轴平台从外到内由外框、中框、内框和台体4个框架组成,各坐标系定义为:OXbYbZb为与基座固联的坐标系;OX3Y3Z3为与外框架固联的坐标系,OY3为内框架轴;OX2Y2Z2为与中框架固联的坐标系,OX2为中框架轴;OX1Y1Z1为与内框架固联的坐标系,OY1为内框架轴;OXPYPZP为与台体固联的坐标系,OZP为台体轴。
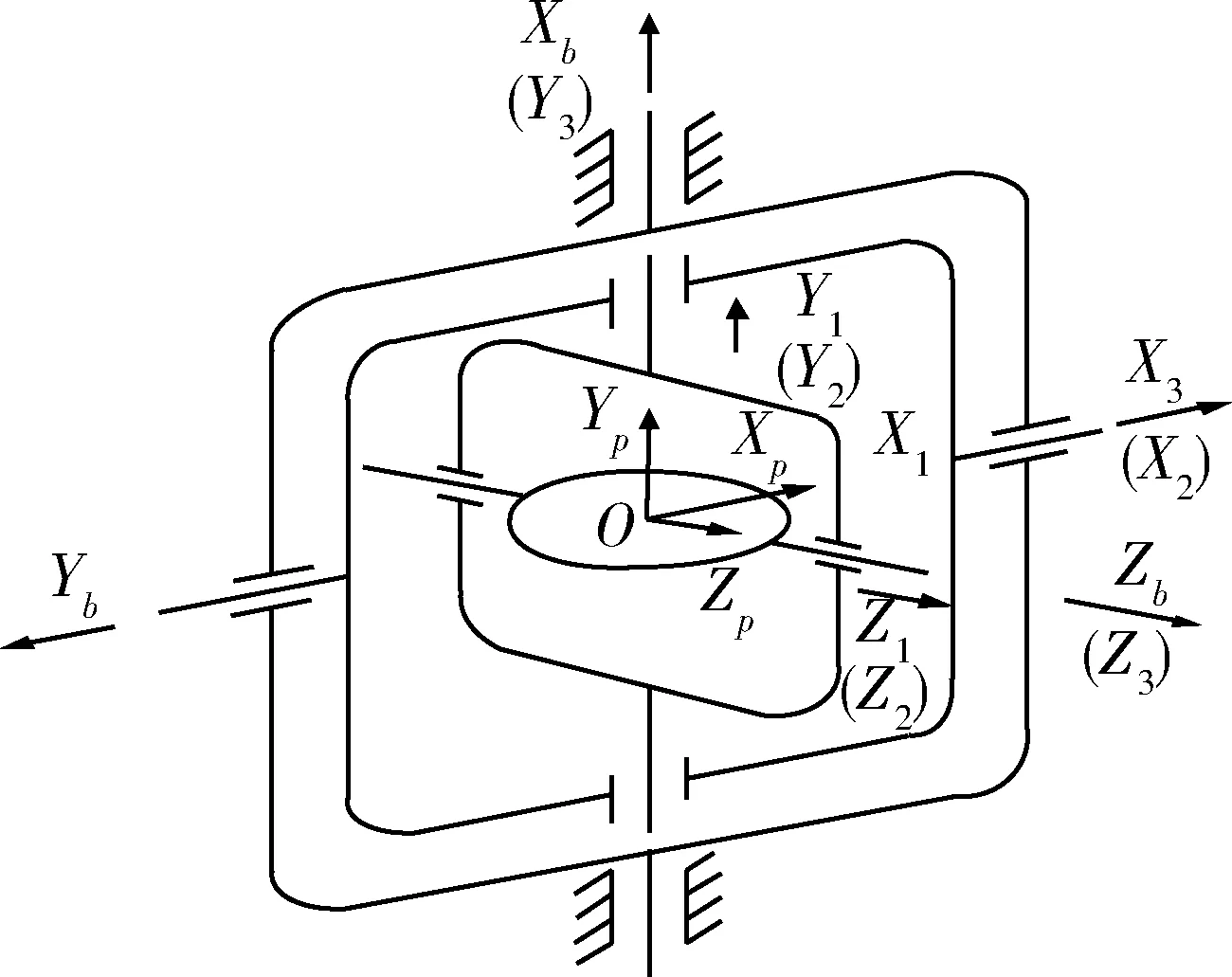
图1 平台框架与坐标系定义

(1)
其中,ωpx,ωpy,ωpz为台体绝对角速度;ωbx,ωby,ωbz为载体绝对角速度;ω1x,ω1y,ω1z为内框架绝对角速度;ω2x,ω2y,ω2z为中框架绝对角速度;ω3x,ω3y,ω3z为外框架绝对角速度。转换矩阵:
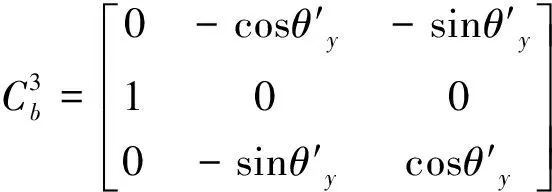
利用式(1)可迭代得到台体角速度、框架角速度和载体角速度间的运动方程:
(2)
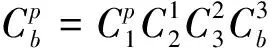
1.2 动力学模型[5]
三框架四轴平台可看做外框架、中框架、内框架和台体绕定点的旋转运动,因此,可根据欧拉方程分别建立四轴的动力方程,也即分别建立台体组合件、内框组合件、中框组合件和外框组合件方程。假设台体组合件结构完全对称,三轴主惯性矩相同,皆为Jp;内环的惯性矩为J1x=J1z=J1xz≠J1y;中环的惯性矩为J2x=J2y=J2xy≠J2z;外环的惯性矩为J3x,J3y,J3z。令Tp,T1,T2,T3分别为台体轴、内框架轴、中框架轴及外框架轴上的力矩电动机驱动力矩;fp,f1,f2,f3分别为台体轴、内框架轴、中框架轴及外框架轴上的干扰力矩,包括摩擦力矩、不平衡负载力矩等。根据参考文献[5]得:
(3)
式中:
J3=J2xy+(J1y+Jp)cos2θy+J1xzsin2θy;
J4=J3x+J2xycos2θx+(J2z+(J1y+Jp)sin2θy+J1xzcos2θy)sin2θx;
J34=J43=(J1y-J1xz+Jp)sinθycosθysinθx。
从式(2)和(3)可以看出,四轴平台轴是相互耦合的,且伴随着相对转角的变化,耦合程度或系数也随之变化。除此之外,外部干扰、模型参数未知及不确定性等各类因素都将影响稳定回路控制的动态性能和静态性能。因此,四轴平台的控制是十分复杂的问题。
1.3 稳定回路
三框架四轴平台是在原来两框架三轴平台的基础上,增加了一个随动框架。三轴平台部分由陀螺仪和稳定回路控制,稳定在惯性空间,而随动框架则由随动回路的控制而始终跟随内框架。本文只研究稳定回路部分,选择单自由度陀螺仪作为稳定回路的惯性敏感器件,由文献[4]可得稳定回路方程:

(4)

令:


(5)
(6)
稳定回路方程式(6)考虑了模型未知、参数不确定以及外界干扰等因素,符合实际系统模型。
2 鲁棒自适应反步控制器设计
为了便于分析问题,给出如下的假设与引理:
假设2 系统的不确定项|Δ1|≤B1,|Δ2|≤B2,其中B1,B2为已知参数。
假设3 系统的不确定参数θ满足θmin≤θ≤θmax,其中θmin,θmax为θ的已知上下界。

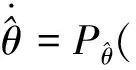
其中,Г为参数辨识速率的正定对角阵,τ为自适应函数,此算法有如下2个特性:

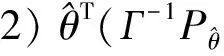

根据反步法的基本原理,定义系统的误差:
(7)
其中,xd为位置期望值;a1,a2为虚拟控制量;z1,z2和z3为控制误差。
1) 对第1个子系统z1=x1-xd,考虑如下的Lyapunov函数:
(8)
对式(8)求导并联合式(7)得:
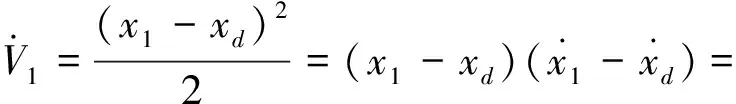
(9)
取虚拟控制律:
(10)
式中,k1为虚拟控制律设计参数,且k1>0,将式(10)代入式(9)得:
(11)
2)选取如下的Lyapunov函数:
(12)
对式(12)求导,并联合式(7)得:

(13)
取虚拟控制律:
(14)

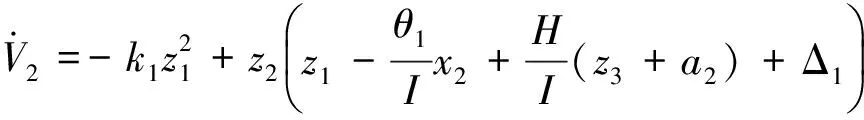
(15)

3)选取如下的Lyapunov函数:
(16)
对式(16)求导得:
(17)
由式(7)得:
(18)

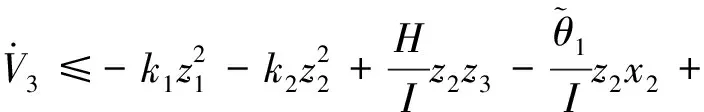
(19)
取控制律:
(20)
将式(20)代入式(19)得:

(21)

3 稳定性分析

(22)
对式(22)求导,并联合式(21)得:
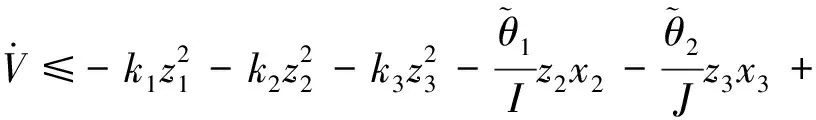
(23)
选择自适应函数:
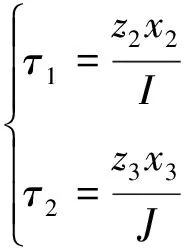
(24)
自适应控制律
(25)
将式(24)和(25)代入式(23),同时联合特性2可得:
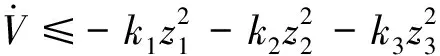
(26)
由式(26)和V≥0,可知Lyapunov函数V是递减有界的,根据引理2可知,整个闭环系统稳定。
4 仿真验证
为了验证本文提出的鲁棒自适应反步法的有效性和优越性,用MATLAB进行了仿真验证,并与传统的PID算法作对比试验。陀螺仪参数:H=230g·cm·s,I=0.153g·cm·s2,D=25g·cm·s;框架轴参数:J=320 g·cm·s2,C=40g·cm·s;力矩电机提供最大力矩为Tn=40000g·cm:PID控制器参数:P=42,I=190,D=2;鲁棒自适应反步法控制器参数:D1=0.004/I,D2=0.04/J,η1=2,η2=2,k1=36,k2=8,k3=5。设干扰力矩及未建模参数:Δ1=0.002g·cm,Δ2=0.02g·cm,上述条件下分别采用传统PID控制和本文提出的鲁棒自适应反步法控制方法,在MATLAB/SIMULINK下进行仿真,仿真结果如图2。

图2 台体轴扰动力矩下的转动角度β响应曲线
由图2仿真结果可得PID控制算法台体轴转动角度最大值为0.031rad,稳定时间为0.4s,超调量为0.0012rad,系统稳态误差为9×10-5rad;鲁棒自适应反步法控制方法台体轴转动角度最大值为0.0091rad,稳定时间为0.2s,系统无超调,系统稳态误差为1.3×10-5rad。
5 结论
针对存在模型未知、不确定参数以及外界干扰项的平台系统稳定回路,提出了一种鲁棒自适应反步控制方法。首先,建立了平台系统的数学模型,开展了平台四框架运动学及动力学分析;其次,充分考虑系统参数的模型未知、参数不确定以及外界干扰的因素,建立了平台稳定回路方程;再次,结合反步法理论,设计了合适的虚拟控制量,来补偿外界干扰对稳定回路的影响;最后利用Lyapunov稳定性理论和光滑投影算法, 设计了参数自适应律,实现了对稳定回路中未知参数的估计。
参 考 文 献
[1] Hilkert J M. Inertially Stabilized Platform Technology Concepts and Principles[J]. Control Systems IEEE, 2008, 28(1):26-46.
[2] Leghmizi S, Liu S, et al. Modeling, Design and Control of a Ship Carried 3 DOF Stabilized Platform[J]. Research Journal of Applied Sciences, Engineering and Technology, 2012, 4(19): 3843-3851.
[3] Safa A, Abdolmalaki R Y. Robust Output Feedback Tracking Control for Inertially Stabilized Platforms With Matched and Unmatched Uncertainties[J]. IEEE Transactions on Control Systems Technology, 2017, PP(99):1-14.
[4] 邓益元. 静压液浮陀螺平台系统[M]. 北京: 中国宇航出版社,2012.
[5] 高钟毓. 惯性导航系统技术[M]. 北京: 清华大学出版社, 2012.
[6] 秦永元. 惯性导航[M]. 北京: 科学出版社, 2006.
[7] 王巾, 王凯. 高精度陀螺稳定平台稳定回路设计[J]. 光电技术应用, 2012, 27(3): 26-29.(Wang Jin, Wang Kai. Design of Stabilized Loop for High Precision Gyro-stabilized Platform[J]. Electro-Optic Technology Application, 2012, 27(3): 26-29.)
[8] Li S S, Zhong M Y. Design of Control System Based on PID of Three-axis Inertially Stabilized Platform for Airborne Remote Sensing[J]. Journal of Jilin University, 2011.
[9] Li B, Hullender D, Direnzo M. Nonlinear Induced Disturbance Rejection In Inertial Stabilization Systems[J]. IEEE Transactions on Control Systems Technology, 2015, 6(3):421-427.
[10] Li Z, Fan D, Fan S. LuGre-Model-Based Friction Compensation in Direct-Drive Inertially Stabilized Platforms[J]. Ifac Proceedings Volumes, 2013, 46(5):636-642.
[11] Fang J C, Zi-Hui Q I, Zhong M Y. Feedforward Compensation Method for Three Axes Inertially Stabilized Platform Imbalance Torque[J]. Journal of Chinese Inertial Technology, 2010.
[12] 程婧容,杨庆明,谈振藩. 惯性平台稳定回路的变结构控制[J]. 中国惯性技术学报,1999,7(4):73-76.(Cheng Jingrong, Yang Qingming, Tan Zhenfan. The Variable Structure Control of the Stabilizing Circuits for Inertial Platform[J]. Journal of Chinese Inertial Technology, 1999, 7(4): 73-76.)
[13] 牛立,李莉,庄良杰. 惯性平台稳定回路的自抗扰控制[J]. 中国惯性技术学报, 2004, 12(6): 48-51. (Niu Li, Li Li, Zhuang Liangjie. Active Disturbance Rejection Control of Stabilizing Circuits for Inertial Platform [J]. Journal of Chinese Inertial Technology, 2004, 12(6): 48-51.)
[14] Moorty J, Rajeev M, Sule V. H∞Control Law for Line-of-sight Stabilization for Mobile Land Vehicles [J]. Optical Engineering, 2002,4(11):2935-2944.
[15] Liu W, Zhou X. Nonlinear Friction Modeling and Adaptive Compensation on an Inertially Stabilized Platform System for Aerial Remote Sensing Application [J]. Journal of Mechanical Engineering, 2013,49(15):122-127.
[16] 李红光, 鱼云岐, 宋亚民. 最优控制在车载惯性平台稳定回路中的应用[J]. 应用光学, 2007, 28(3):251-256. (Li Hongguang, Yu Yunqi, Song Yamin. Application of Optimal Control for Stabil Ization Loop of Vehicle Inertial Platform [J]. Journal of Applied Optics, 2007, 28(3):251-256.)
[17] 郭健, 姚斌, 吴益飞. 具有输入齿隙的一类非线性不确定系统自适应鲁棒控制[J]. 控制与决策, 2010, 25(10):1580-1584. (Guo Jian, Yao Bin, Wu Yifei. Adaptive Robust Control for a Class of Nonlinear Uncertain System with Input Backlash [J]. Control and Decision, 2010, 25(10):1580-1584.)
[18] 焦晓红,吴新平.非线性系统分析与设计[M]. 北京:北京工业出版社, 2006.

