基于事件起点的层次化时序Petri网及其电网故障诊断方法

赖宏毅,汪 旸,杨 雯,周超凡,徐 彪,尹项根,简 程

(1. 国家电网华中电力调控分中心,湖北 武汉 430077;2. 华中科技大学 强电磁工程与新技术国家重点实验室,湖北 武汉 430074)

0 引言

当电网发生故障时,快速准确的故障诊断对加快事故处理和系统恢复进程、保证电力系统的安全可靠运行至关重要。然而随着电网的不断发展和互联,在故障发生后的短时间内,保护及断路器动作等大量告警信息涌向调度中心,且可能伴随信息缺失、畸变等不确定性,利用告警信息快速准确地识别故障元件能为电网实时调控运行提供重要的决策支持。

目前较为实用的电力系统故障诊断方法主要包括基于专家系统[1]和基于解析模型[2-4]的方法。此外,人工神经网络[5]、贝叶斯网络[6]、支持向量机[7]、Petri网[8]等理论方法也逐步应用于电力系统故障诊断研究。其中,Petri网因推理过程简单、物理意义清晰、推理逻辑严密一直是电网故障诊断研究领域的热点,模糊Petri网的提出有效弥补了传统Petri网在处理不确定性问题上的缺陷。文献[9]提出了基于加权模糊推理Petri网的电网故障诊断模型,通过优化模型结构来降低模型矩阵的规模,提高了诊断的准确性和速度;文献[10]提出基于方向性加权模糊Petri网的诊断方法,通过分别在各故障蔓延方向上建立诊断模型,以改善模型的容错性和对网络拓扑变化的适应性。为消除时序不一致和错误告警信息的影响,文献[11]利用保护和断路器的动作时序关系,建立与某元件相关的多个库所时序关联矩阵,对比典型时序关联模型对保护和断路器的告警信息进行纠错;文献[12]对线路两侧不同保护、断路器之间的时序进行交叉检查,得到保护与断路器之间时序配合的一致性并修正诊断模型;文献[13]考虑元件故障、保护动作和断路器跳闸之间的延时约束,通过将时序约束网络和模糊Petri网进行融合实现错误警报的自动过滤。

上述方法应用于电网故障诊断有一定的容错性和适应性,但存在以下局限:①对于告警信息时序特性的利用主要局限于告警信息的筛选和验证阶段,难以制定完善的告警信息时序比较规则,且说服力不强;②时序信息计算量大,难以满足电力系统在线诊断的需求;③在保护和断路器误动/拒动、告警信息缺失/错误的情况下,模型的容错性不强,处理复杂故障时可能得不到明确的诊断结果。

在上述背景下,本文提出一种基于事件起点的层次化加权模糊时序Petri网TWFPN(Temporal Weighted Fuzzy Petri Net)故障诊断方法,以故障发生时刻作为事件起点,提出基于事件起点的保护和断路器时序约束检查方法,针对可疑故障元件的TWFPN模型,通过逆向时序推理获得该元件的故障时间点约束,再通过正向时序推理对告警信息的初始置信度予以修正,IEEE 39节点系统仿真算例和电网实际故障算例表明该方法能够在保护和断路器误动/拒动、告警信息缺失/错误等复杂状态下识别真实故障元件,提高了故障诊断的准确度和容错性。通过与现有应用时序信息的故障诊断方法相比,本文提出的故障诊断方法充分利用了报警信息的时序信息与约束关系,时序推理过程简明清晰,对网络拓扑的变化适应性强,运算速度快,满足在线诊断需求。

1 TWFPN

1.1 TWFPN的定义

传统的模糊Petri网(FPN)[14]考虑了保护和断路器动作的不确定性以及误动/拒动的可能性,采用加权方式描述不同保护和断路器动作对诊断结果的影响,通常定义为一个8元组:SFPN={P,R,I,H,O,W,M,U}。其中，P=[p1,p2,p3,…,pm](m≥0)为m维库所向量,用于表示命题,m为库所数量;R=[r1,r2,r3,…,rn](n≥0)为n维变迁向量,用于表示推理规则,n为变迁数量;I=(δij)m×n为直接输入矩阵,表示库所P到变迁R的映射关系,δij∈{0,1},当库所pi存在到变迁rj的直接有向弧,即pi是rj的直接输入时,δij=1,否则δij=0;H=(γij)m×n为抑制输入矩阵,γij∈{0,1},当库所pi存在到变迁rj的抑制输入弧,即pi是rj的抑制输入时,γij=1,否则γij=0;O=(ζij)n×m为输出矩阵,ζij∈{0,1},表示变迁R到库所P的映射关系,当变迁ri存在到库所pj的有向弧,即pj是ri的输出时,ζij=1,否则ζij=0;W=(ωij)m×n为输入弧的权值矩阵,ωij∈{0,1},表示命题对相应规则的影响程度;M=[M1,M2,M3,…,Mm]T为m维库所置信度向量,Mi表示库所pi对应的命题为真的置信度,库所的初始置信度向量用M0表示;U=diag(μ1,μ2,μ3,…,μn)为规则的置信度矩阵,μi为变迁ri的置信度。

鉴于篇幅限制,TWFPN的运算规则及推理过程此处不详述,具体可参考文献[10-11]。

为了充分利用保护和断路器的动作时序信息和约束关系,本文研究一种基于事件起点的层次化TWFPN,f为可疑故障元件,将元件f故障发生的时刻tf定义为事件起点,引入保护动作时限约束以及保护动作和对应断路器跳闸之间的时间约束,通过时序约束检查来修正其对应的初始置信度向量M0,将TWFPN定义为一个11元组:STWFPN={P,R,I,H,O,W,M,U,t,T,D}。

其中，P、R、I、H、O、W、M、U与前述定义一致；t=[tp1,tp2,tp3,…,tpm](m维)为系统获取的库所初始状态信息发生时间,tpi对应库所pi的告警信息获取时间点;T={T(tpi)|pi∈P}为时间点约束集合,与t中元素相对应,T(tpi)表示库所pi对应的告警信息应该出现的时间区间;D={D(tf,tpi)|pi∈P}为时间距离约束集合,D(tf,tpi)表示库所pi所对应的告警信息的获取时间与事件起点tf之间的时间距离约束。

1.2 TWFPN中的时序约束

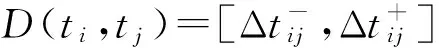
定义TWFPN模型中各初始库所的时序属性为{pi,tpi,T(tpi),D(tf,tpi)},过渡库所无实际物理意义,不具备时序属性。时序属性描述了库所pi告警信息的获取时间、时间点约束及与事件起点间的时间距离约束。其中,tpi可直接获取,若没有则此项为空;T(tpi)需根据后文2.3节中基于事件起点的保护和断路器的时序约束检查方法来确定;D(tf,tpi)根据保护和断路器的动作规则确定。

电网故障后的告警信息主要包含各保护和断路器动作信息及其发生时刻,可将其表达为保护出口动作时刻(R,tR)和断路器跳闸时刻(CB,tCB)。为保证保护动作的选择性,不同保护设定了不同的动作延时,保护动作时刻和其对应断路器的跳闸时刻之间也存在着时间约束。定义D(tf,tm)、D(tf,tmf)、D(tf,ts)分别为元件故障到主保护、断路器失灵保护、远后备保护动作的时间距离约束,D(tR,tCB)为保护动作到其对应的断路器跳闸的时间距离约束。给定各时间距离约束[16]为:

D(tf,tm)=[10,40] ms,D(tf,ts)=[600,1 100] ms

D(tf,tmf)=[300,500] ms,D(tR,tCB)=[40,60] ms

TWFPN模型中所有告警信息都可转换到以事件起点为基准的时间距离约束下,保护动作告警信息相对于事件起点的时间距离约束为D(tf,tR),断路器跳闸告警信息相对于事件起点的时间距离约束为D(tf,tCB)=D(tf,tR)+D(tR,tCB)。

2 基于事件起点的层次化TWFPN电网故障诊断模型

以图1所示的IEEE 10机39节点系统为例,说明基于事件起点的层次化TWFPN模型的构建方法。

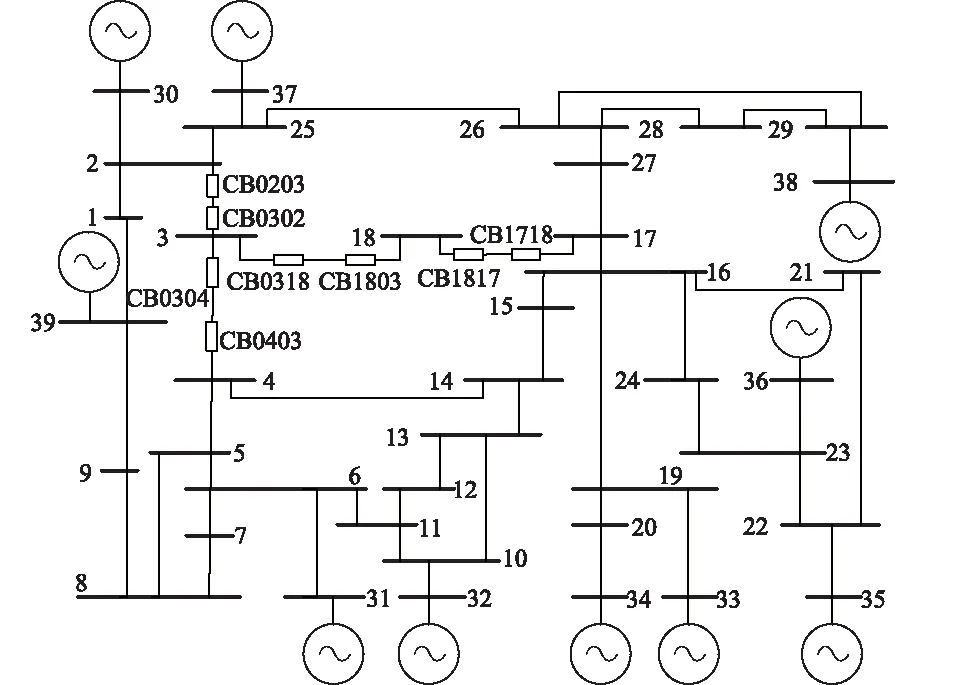
图1 IEEE 10机39节点系统Fig.1 IEEE 10-generator 39-bus system

Petri网运用图形化的表示方法对于描述具有一定逻辑关系的离散事件具有很大的优势,且可以应用矩阵分析方法进行推理,但当对大规模复杂电网运用Petri网进行建模时,可能出现矩阵维数太大、组合爆炸以及模型的适应能力差等问题,本文采用层次化建模的方法,通过分析故障发生后的保护和断路器动作过程,反向建立母线和线路层次化的TWFPN模型。本文在建模时对元件的保护配置考虑如下:每条线路的两端都配置了主保护、断路器失灵保护以及远后备保护;每条母线配置了主保护和相邻线路上的远后备保护。其他保护配置情况则可以根据实际的保护配置对模型作相应调整即可。对下文中的Petri网符号备注如下:B表示母线,L表示线路,CB表示断路器,R表示保护,并用m、mf和s分别表示主保护、断路器失灵保护和远后备保护,R0318m表示线路L0318靠近母线B03一侧的主保护,R1803m表示线路L0318靠近母线B18一侧的主保护,其他依此类推。

2.1 母线和线路的层次化TWFPN模型

当线路发生故障时,首先由线路两端各自的主保护动作于相应断路器跳闸,当某个断路器拒动时启动该断路器的失灵保护跳开该线路母线背侧断路器,当主保护和断路器失灵保护动作失败后,由远后备保护动作隔离故障。根据线路故障后的保护和断路器动作过程,反向建立其层次化TWFPN模型,即先对线路两端分别建立主保护、断路器失灵保护、远后备保护诊断子网,再联合3个保护诊断子网形成各端的诊断虚拟库所,最后联合两端的各自虚拟库所得到最后的综合诊断结果。以图1中的线路L0318为例建立的层次化TWFPN模型,如图2所示。图中，p1、p2、…、p19为初始库所；p20、p21、…、p27为过渡库所；p28为原因库所；r1、r2、…、r6为保护动作变迁；r7、r8、…、r13为过渡变迁。

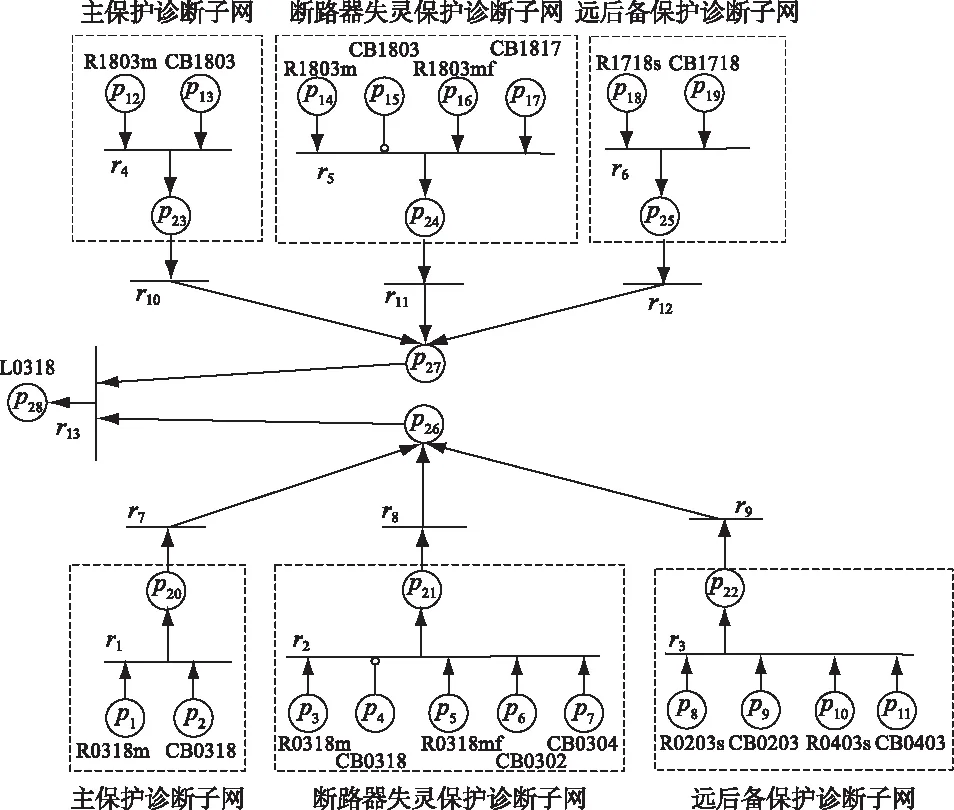
图2 L0318的层次化TWFPN模型Fig.2 Hierarchical TWFPN model of L0318

类似地,可以构造母线的层次化TWFPN模型,先对每个母线出线方向建立主保护和远后备保护诊断子网,再联合2个保护诊断子网形成各出线方向的诊断虚拟库所,最后联合各出线方向的虚拟库所得到最后的综合诊断结果。针对图1中的母线B18,建立的层次化TWFPN模型如图3所示。图中，p1、p2、…、p8为初始库所；p9、p10、…、p14为过渡库所；p15为原因库所；r1、r2、r3、r4为保护动作变迁；r5、r6、…、r9为过渡变迁。

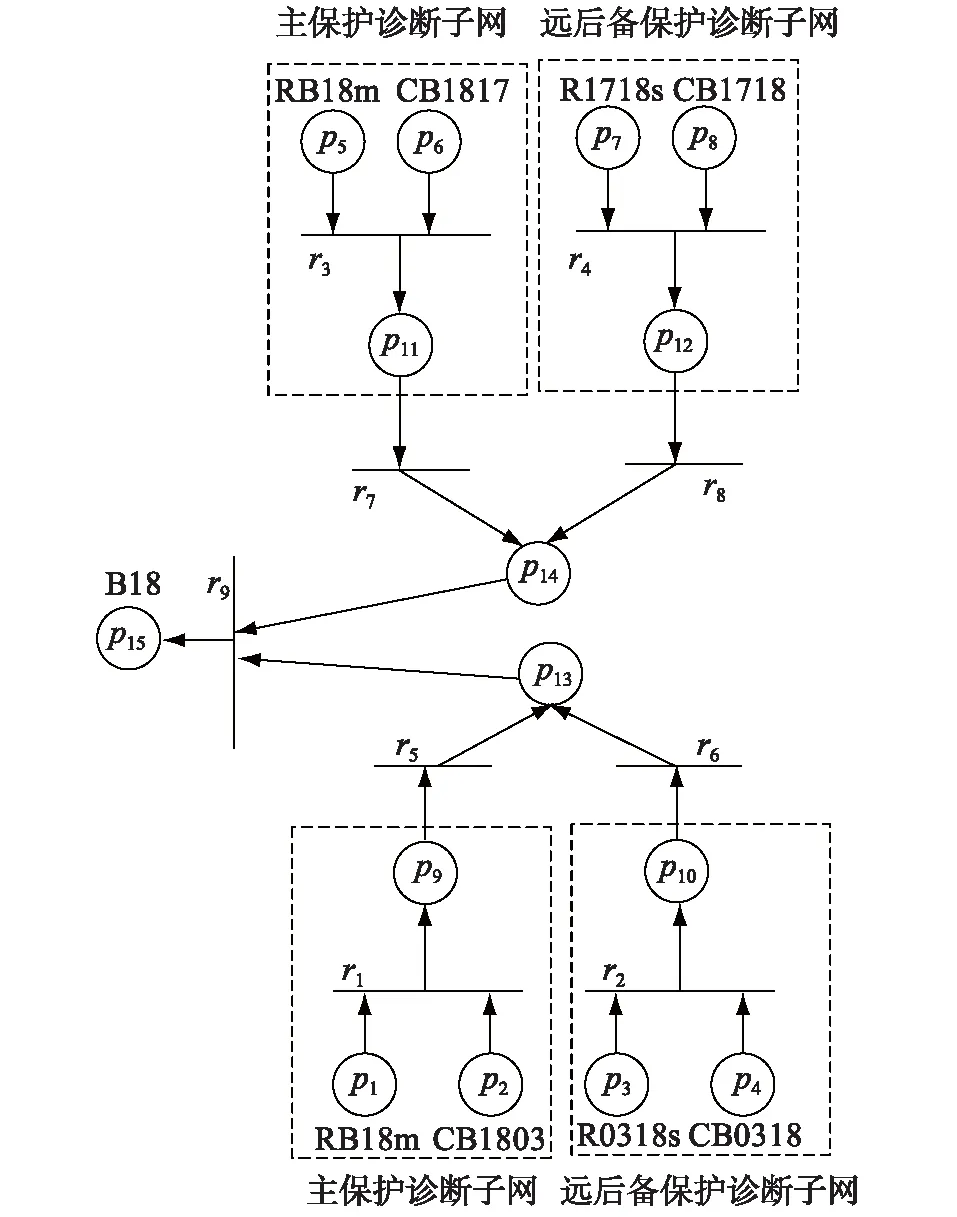
图3 B18的层次化TWFPN模型Fig.3 Hierarchical TWFPN model of B18

2.2 TWFPN模型参数设置

a. 输入弧权值。

在元件的TWFPN模型中,保护和断路器对应的输入弧权值代表了其对诊断结果的影响差别,目前相关文献中输入弧权值大多根据经验人为设定[10,12,17],本文认为一方面保护动作是断路器动作的前提,元件故障后通常是由保护动作引发断路器跳闸,另一方面保护动作与元件故障的关联性更大,一种保护通常与相应元件故障直接关联,而一个断路器可由多种保护触发使其跳闸,断路器跳闸与故障元件之间指向性不明显,需通过相关保护来加强其判断,因此保护相较于断路器,对故障诊断结果的影响更大。对于某一具体变迁,将输入库所中保护部分和断路器部分对应的输入弧的权值分别设定为0.6和0.4;对线路综合诊断模型中两端诊断虚拟库所对应的输入弧权值分别设定为0.5和0.5;对母线综合诊断模型中各出线方向的诊断虚拟库所对应的输入弧权值设为1/α,α表示这条母线的出线数。

b. 库所初始置信度。

电网故障后保护和断路器存在误动、拒动的风险,上传到调度中心的告警信息也可能伴随信息缺失、畸变等不确定性。对保护和断路器对应的库所,应根据不同的保护和断路器警报信息对故障诊断的作用差别给定库所的初始置信度,初始置信度的设置基于全国电网继电保护与安全自动装置动作情况统计,具体赋值如表1所示[12]。

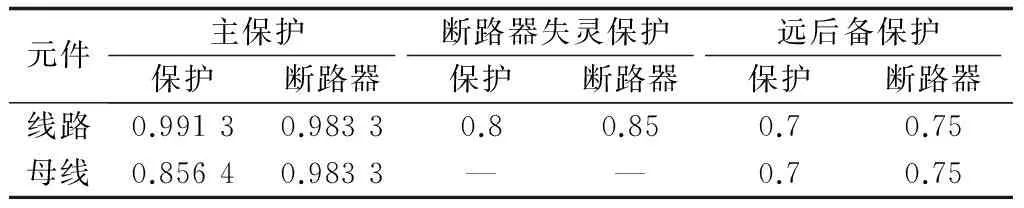
表1 已动作的保护和断路器对应库所的初始置信度Table 1 Initial confidence level of corresponding library to operated protection and circuit breaker

考虑到保护和断路器警报信息中可能夹杂着拒动信息以及信息存在丢失的情况,对未收到告警信息的保护和断路器对应的库所给定一个较小的置信度,如表2所示。

表2 未动作的保护和断路器对应库所的初始置信度Table 2 Initial confidence level of corresponding library to non-operated protection and circuit breaker

过渡库所和原因库所的初始置信度设为0。

c. 变迁置信度。

考虑到不同类型的保护其原理、性能及可靠性都不一样,故在反向的诊断推理过程中对诊断结果的影响程度也不一样,据此赋予变迁不同的置信度[17],规定主保护、断路器失灵保护、远后备保护的变迁置信度分别为1、0.95和0.85,过渡变迁无物理意义,将其置信度设为1。

2.3 基于事件起点的保护和断路器时序约束检查

在1.2节TWFPN的时序约束介绍的基础上,根据各告警信息的获取时间与事件起点之间的时间距离约束进行保护和断路器的时序约束检查,包括2个过程:通过逆向时序推理获取故障发生的时间区间;再通过正向时序推理对保护动作信息和断路器跳闸信息进行检查,并修正其对应库所的置信度。

对下文中的时序约束检查过程中的符号备注如下:T(f)表示可疑故障元件f事件起点的时间点约束,表示事件起点tf应该出现的时间区间,特殊地,T(fs)表示由各个保护及断路器告警信息逆向推理直接得到的事件起点的第一推算时间点约束,T(f)r表示在T(fs)的基础上经过时序约束合并得到的事件起点的第二推算时间点约束。

a. 逆向时序推理。

结合可疑故障元件f的TWFPN模型,利用其相关告警信息获取时间tpi和时间距离约束D(tf,tpi)进行逆向时序推理来获取事件起点的时间点约束,即:

T(f)=tpi-D(tf,tpi)

由各个保护及断路器告警信息得到的事件起点的第一推算时间点约束分别为T(f1)、T(f2)、…、T(fs)。

若T(f1)∩T(f2)∩…∩T(fs)≠∅,即当第一推算时间点约束有区间重叠时,说明f是这些保护和断路器告警信息共同的原因事件,即元件f的故障导致了相关保护和断路器的动作。将第一推算时间点约束直接求交集,得到事件起点唯一的第二推算时间点约束T(f)1=T(f1)∩T(f2)∩…∩T(fs)。

若T(f1)∩T(f2)∩…∩T(fs)=∅,即当第一推算时间点约束没有共同的重叠区间时,说明这些保护和断路器告警信息中存在一部分不是以故障元件f作为原因事件的,而是由其他故障导致的告警信息或者是错误的告警信息,需对其进行筛选和置信度修正。分别将有重叠区间的第一推算时间点约束合并,得到可疑故障元件f的可能的多个第二推算时间点约束T(f)1、T(f)2、…、T(f)r。

b. 正向时序推理。

针对可疑故障元件f的每个第二推算时间点约束,分别进行正向时序推理,得到TWFPN中各初始库所的时间点约束，即：

T(tpi)=T(f)r-D(tf,tpi)

将各初始库所告警信息获取时间点tpi与基于事件起点进行正向推理得到的各初始库所的时间点约束T(tpi)进行对比分析。如果各初始库所的告警获取时间满足时间点约束条件,则认为该库所的状态信息是支持可疑故障元件f在该事件起点下的TWFPN的诊断推理的,将该库所的置信度提高。由于线路主保护及其对应的断路器、母线主保护对应的断路器初始置信度值已经很高,接近于1,不必进行修正。其余保护及断路器在初始置信度值的基础上增加0.1;如果不满足时间点约束条件,将该库所的置信度降低,设为0.1;没有收到告警信息的库所置信度仍设为0.2;过渡库所和原因库所的置信度仍为0。

3 基于事件起点的层次化TWFPN电网故障诊断流程

基于事件起点的层次化TWFPN的电网故障诊断流程如下：

a. 根据收到的保护和断路器告警信息,利用结线分析法进行搜索,得到故障区域,确定可疑故障元件集(f1,f2,…,fk);

b. 针对各个可疑故障元件fk建立层次化的TWFPN模型,获取各初始库所的时序属性;

c. 结合fk的TWFPN模型,根据该模型中各个初始库所告警信息获取时间和时间距离约束进行逆向时序推理,并将有重叠区间的时序约束合并,得到fk基于事件起点的可能的多个第二推算时间点约束T(f)1、T(f)2、…、T(f)r;

d. 针对得到的可疑故障元件fk的事件起点的第二推算时间点约束,进行正向时序推理,可以得到TWFPN中事件起点为T(f)r下各初始库所的时间点约束T(tpi),将其与各初始库所告警获取时间点tpi进行对比分析,修正初始库所的置信度;

e. 结合fk的TWFPN的诊断模型,进行矩阵推理计算,得到fk在时间点约束T(f)r下的故障置信度;

f. 针对可疑故障元件fk的事件起点的可能的多个第二推算时间点约束,重复步骤d、e得到可疑故障元件不同时间点约束下的多个可能的故障置信度,通过对比取最大值为fk的最终故障置信度,对应的时间点约束即为故障发生的时间区间;

g. 针对故障元件集中每个可疑元件,重复步骤b—f，综合得到诊断结果；

h. 根据诊断结果,将故障元件TWFPN模型中各初始库所告警获取时间点tpi与其在事件起点下的时间点约束T(tpi)进行对比分析,以判断保护与断路器的拒动、误动及漏报、误报情况。

故障置信度阈值的设定十分重要,是判断元件故障与否的重要依据,必须保证在故障后保护和断路器的极端动作情况下,也能准确地判别出故障。考虑存在一个告警信息出错的情况,当线路两端或母线各出线方向均由远后备保护动作切除故障时,元件的故障置信度最小,为0.518 5,因此本文取故障置信度的阈值为0.518 5,判定大于0.518 5的元件发生故障,否则认为无故障。

4 算例仿真分析与比较

以图1所示IEEE 39节点系统为例,故障后调度中心收到的告警信息为(R1803m,0)、(R0318m,2)、(RB03m,5)、(CB0302,58)、(CB0304,63)、(R1803mf,320)、(CB1817,368),时标以收到的第一个告警信息时间点为基准,单位为ms。用层次化TWFPN模型对该案例进行故障诊断,完整诊断流程如下。

首先利用结线分析法搜索故障区域,得到可疑故障元件为线路L0318、母线B03和母线B18,分别建立其层次化TWFPN模型。

根据图2所示L0318的层次化TWFPN模型,收集与L0318相关的告警信息,可得(R1803m,0)、(R0318m,2)、(CB0302,58)、(CB0304,63)、(R1803mf,320)、(CB1817,368)。根据各初始库所报警信息获取时间点和时间距离约束进行逆向时序推理,得到L0318事件起点的第一推算时间点约束为:

T(L03181)=tR1803m-D(tf,tm)=[-40，10] ms

T(L03182)=tR0318m-D(tf,tm)=[-38，-8] ms

T(L03183)=tCB0302-D(tf,tm)-D(tR，tCB)=

[-502，-282] ms

T(L03184)=tCB0304-D(tf,tm)-D(tR，tCB)=

[-497，-277] ms

T(L03185)=tR1803mf-D(tf,tmf)=[-180,-20] ms

T(L03186)=tCB1817-D(tf,tmf)-D(tR，tCB)=

[-192，-28] ms

T(L03181)∩T(L03182)∩T(L03183)∩T(L03184)∩T(L03185)∩T(L03186)=∅,分别将有重叠区间的时间点约束合并,得到L0318事件起点的第二推算时间点约束T(L0318)1=[-38,-10] ms和T(L0318)2=[-497,-282] ms。

针对T(L0318)1=[-38,-10] ms进行正向时序推理,得到各初始库所的时间点约束为:

T(R1803m)=T(L0318)1+D(tf,tm)=[-28,30] ms

T(CB0302)=T(CB0304)=T(CB1817)=

T(L0318)1+D(tf,tmf)+D(tR,tCB)=

[302,550] ms

T(R1803mf)=T(L0318)1+D(tf,tmf)=[262,490] ms

将各报警信息获取时间与其时间点约束进行对比分析,R1803m、R0318m、R1803mf、CB1817告警获取时间满足其时间点约束,RB03m、CB0302、CB0304不满足其时间点约束,修正库所的置信度向量为M0=[0.991 3,0.2,0.991 3,0.2,0.2,0.85,0.85,0.2,0.2,0.2,0.2,0.991 3,0.2,0.991 3,0.2,0.9,0.95,0.2,0.2,0,0,0,0,0,0,0,0,0]T,根据L0318的层次化TWFPN模型列出其余网络矩阵参数,通过矩阵推理计算得到最终的库所置信度向量为M=[0.991 3,0.2,0.991 3,0.2,0.2,0.1,0.1,0.2,0.2,0.2,0.2,0.991 3,0.2,0.991 3,0.2,0.9,0.95,0.2,0.2,0.674 78,0.349 02,0.17,0.674 78,0.907 89,0.17,0.674 78,0.907 89,0.7913 35]T,库所L0318的置信度为0.791 335,即该时间点约束下L0318的故障置信度为0.791 335。

类似地,针对T(L0318)2=[-497,-282] ms进行正向时序推理并修正库所的置信度向量为M0=[0.1,0.2,0.1,0.2,0.2,0.95,0.95,0.2,0.2,0.2,0.2,0.1,0.2,0.1,0.2,0.1,0.1,0.2,0.2,0,0,0,0,0,0,0,0,0]T,通过矩阵推理计算得到库所L0318的置信度为0.327 75。

通过对比在T(L0318)1=[-38,-10] ms和T(L0318)2=[-497,-282] ms下的故障置信度,取较大值0.791 335为L0318的最终故障置信度,对应的时间点约束[-38,-10] ms即为故障发生的时间区间。

类似地,构建B03和B18的TWFPN模型,利用其相关报警信息进行故障诊断,诊断结果如表3所示。

综合以上诊断结果,判定L0318和B03分别在[-38,-10] ms和[-35,-5] ms发生故障,B18无故障,根据故障元件TWFPN模型中各初始库所的时间点约束,对比实际告警信息的获取时间,分析得到如下结论:L0318故障后,线路两端主保护正确动作,跳开线路两端断路器,CB0318正确动作但其报警信息丢失,CB1803拒动,由CB1803的断路器失灵保护动作跳开CB1817以隔离故障；B03故障后,母线主保护正确动作跳开与母线相连的断路器CB0318、CB0302和CB0304,CB0318告警信息丢失。

用本文所提出的故障诊断方法对测试系统中的多种故障场景进行测试,并且将其与文献[12]、[15]的诊断结果进行对比,部分测试结果如表4所示。

表中,案例1—3为信息完备情况下的诊断,虽然保护和断路器的误动、拒动导致了故障区域的扩大,但利用本文提出的基于事件起点的层次化TWFPN方法可以识别出误动或拒动信息而得出正确的诊断结果；案例4—7模拟存在保护和断路器误动、拒动以及告警信息缺失/错误等复杂状况下的故障诊断,本文提出的方法均能准确地得到诊断结果,提高了故障诊断的准确度和容错性。

表3 故障案例诊断结果Table 3 Diagnosis results of fault case

对广州地区电力系统实际故障案例[15]进行测试,鉴于篇幅限制,层次化TWFPN的建立及故障诊断的步骤和过程不详细给出,可疑故障元件的故障置信度及时间点约束分别为(L2943,0.890 32,[-38,-21] ms)和(B4,0.434 99,[232,278] ms)。综合诊断结论如下:线路L2943在-38～-21 ms期间发生故障线路两端主保护正确动作并作用于相应断路器跳闸,由于C12拒动,其断路器失灵保护动作跳开母线B4背侧断路器以隔离故障。故障诊断结果和实际发生的故障情况相符。

本文所提的电网故障诊断方法采用MATLAB工具实现,以上述算例为例,在主频为2.6 GHz双核处理器、内存容量为2 GB的PC机上,故障诊断过程所耗时间均在18 ms以内,能够满足电网故障诊断的在线要求。

此外,将本文方法与近年提出的2种利用时序信息的电网故障诊断方法进行了详细的性能对比分析,结果如表5所示。表中,β为收到的报警信息的数目;γ为可疑故障元件的数目。

通过表4中诊断结果的对比和表5中性能的对比可以发现,本文提出的方法充分利用了报警信息的时序信息与约束关系,通过将告警信息全部转换到以故障发生时刻为基准的时序约束关系下,对保护、断路器告警信息进行时序约束检查,不仅可以得到设备的故障时间点约束,在保护和断路器误动/拒动、告警信息缺失/错误等复杂状况下具有较好的容错性,而且对网络拓扑的变化适应性强,时序推理过程简明清晰,运算速度快,满足在线诊断需求。

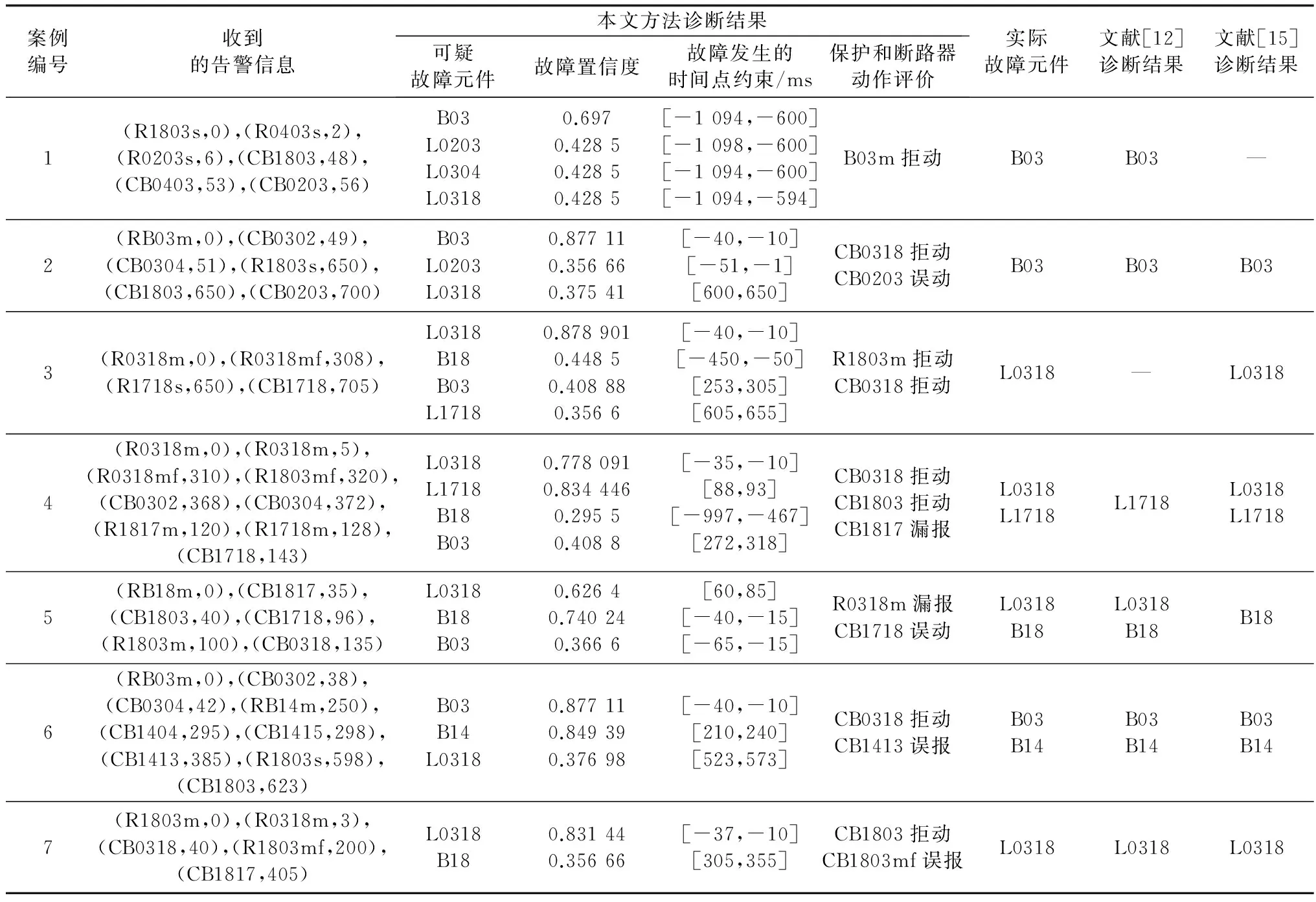
表4 基于事件起点的层次化TWFPN方法的故障案例诊断结果Table 4 Diagnosis results of fault cases for hierarchical TWFPN model based on event-starting point

表5 本文方法与现有方法的对比Table 5 Comparison between proposed method and existing methods

5 结语

本文研究一种基于事件起点的层次化TWFPN故障诊断方法,以故障发生时刻作为事件起点,提出基于事件起点的保护和断路器时序约束检查方法,通过逆向和正向时序推理对保护和断路器动作信息置信度予以修正,提高了故障诊断的准确度和容错性。IEEE 39节点系统仿真算例和电网实际故障算例表明该方法能够在保护和断路器误动/拒动、告警信息缺失/错误等复杂状态下识别真实故障元件,还可以得到设备故障的时间点约束,有利于进一步分析故障原因和故障事态发展。该方法充分利用了报警信息的时序信息与约束关系,时序推理过程简明清晰,对网络拓扑的变化适应性强,运算速度快,满足在线诊断需求,具有良好的应用前景。

参考文献：

[ 1 ] 赵伟,白晓民,丁剑,等. 基于协同式专家系统及多智能体技术的电网故障诊断方法[J]. 中国电机工程学报,2006,26(20):1-8.

ZHAO Wei,BAI Xiaoming,DING Jian,et al. A new fault diagnosis approach of power grid based on cooperative expert system and multi-agent technology[J]. Proceedings of the CSEE,2006,26(20):1-8.

[ 2 ] 张岩,张勇,文福拴,等. 融合信息理论的电力系统故障诊断解析模型[J]. 电力自动化设备,2014,34(2):158-164,174.

ZHANG Yan,ZHANG Yong,WEN Fushuan,et al. Analytical model for power system fault diagnosis integrated with information theory[J]. Electric Power Automation Equipment,2014,34(2):158-164,174.

[ 3 ] 梁辰,邰能灵,胡炎,等. 基于保护信号的隐性故障检测[J]. 电力自动化设备,2016,36(5):154-159.

LIANG Chen,TAI Nengling,HU Yan,et al. Detection of hidden fai-lure based on protection signals[J]. Electric Power Automation Equipment,2016,36(5):154-159.

[ 4 ] 田方媛,张岩,徐兵,等. 多代理系统框架下的主动配电系统故障诊断[J]. 电力自动化设备,2016,36(6):19-26.

TIAN Fangyuan,ZHANG Yan,XU Bing,et al. Fault diagnosis based on multi agent system for active distribution system[J]. Electric Power Automation Equipment,2016,36(6):19-26.

[ 5 ] 熊国江,石东源,朱林,等. 基于径向基函数神经网络的电网模糊元胞故障诊断[J]. 电力系统自动化,2014,38(5):59-65.

XIONG Guojiang,SHI Dongyuan,ZHU Lin,et al. Fuzzy cellular fault diagnosis of power grids based on radial basis function neural network[J]. Automation of Electric Power Systems,2014,38(5):59-65.

[ 6 ] 孙明蔚,童晓阳,刘新宇,等. 运用时序贝叶斯知识库的电网故障诊断方法[J]. 电网技术,2014,38(3):715-722.

SUN Mingwei,TONG Xiaoyang,LIU Xinyu,et al. A power system fault diagnosis method using temporal Bayesian knowledge bases[J]. Power System Technology,2014,38(3):715-722.

[ 7 ] 胡伟,李勇,曹一家,等. 基于LOF和SVM的智能配电网故障辨识方法[J]. 电力自动化设备,2016,36(6):7-12.

HU Wei,LI Yong,CAO Yijia,et al. Fault identification based on LOF and SVM for smart distribution network[J]. Electric Power Automation Equipment,2016,36(6):7-12.

[ 8 ] CALDERARO V,HADJICOSTIS C N,PIICCOLO A. Failure identification in smart grids based on Petri net modeling[J]. IEEE Tran-sactions on Industrial Electronics,2011,58(10):4613-4623.

[ 9 ] LUO Xu,KEZUNOVIC M. Implementing fuzzy reasoning Petri nets for fault section estimation[J]. IEEE Transactions on Power Deli-very,2008,23(2):676-685.

[10] 杨健维,何正友,臧天磊. 基于方向性加权模糊Petri网的电网故障诊断方法[J]. 中国电机工程学报,2010,30(34):42-49.

YANG Jianwei,HE Zhengyou,ZANG Tianlei. Power system fault-diagnosis method based on directional weighted fuzzy Petri nets[J]. Proceedings of the CSEE,2010,30(34):42-49.

[11] 杨健维,何正友. 基于时序模糊Petri网的电力系统故障诊断[J]. 电力系统自动化,2011,35(15):46-51.

YANG Jianwei,HE Zhengyou. Power system fault diagnosis approach based on time sequence fuzzy Petri net[J]. Automation of Electric Power Systems,2011,35(15):46-51.

[12] 童晓阳,谢红涛,孙明蔚. 计及时序信息检查的分层模糊Petri网电网故障诊断模型[J]. 电力系统自动化,2013,37(6):63-68.

TONG Xiaoyang,XIE Hongtao,SUN Mingwei. Power system fault diagnosis model based on layered fuzzy Petri net considering temporal constraint checking[J]. Automation of Electric Power Systems,2013,37(6):63-68.

[13] 张岩,张勇,文福拴,等. 容纳时序约束的改进模糊Petri网故障诊断模型[J]. 电力系统自动化,2014,38(5):66-72.

ZHANG Yan,ZHANG Yong,WEN Fushuan,et al. Power system fault diagnosis with an enhanced fuzzy Petri net accommodating temporal constraints[J]. Automation of Electric Power Systems,2014,38(5):66-72.

[14] LI Xiaoou,LARA-ROSANO F. Dynamic knowledge inference and learning under adaptive fuzzy net framework[J]. IEEE Transactions on Systems,Man,and Cybernetics:Part C Applications and Reviews,2008,30(4):442-450.

[15] 郭文鑫,文福拴,廖志伟,等. 基于时序约束网络的电力系统在线警报处理解析模型[J]. 电力系统自动化,2009,33(21):36-42,65.

GUO Wenxin,WEN Fushuan,LIAO Zhiwei,et al. An analytic model for power system online alarm processing based on temporal constraint network[J]. Automation of Electric Power Systems,2009,33(21):36-42,65.

[16] 乐全明. 电网高级智能故障诊断系统中关键技术的研究[D].上海：上海交通大学,2006.

LE Quanming. Research on key techniques of advanced intelligent fault diagnosis system for power grid[D]. Shanghai:Shanghai Jiao Tong University,2006.

[17] 陈强,程学珍,刘建航,等. 基于分层变迁的WFPN电网故障分析[J]. 电工技术学报,2016,31(15):125-135.

CHEN Qiang,CHENG Xuezhen,LIU Jianhang,et al. The analysis method of power grid fault based on hierarchical transition weighted fuzzy Petri net[J]. Transactions of China Electrotechnical Society,2016,31(15):125-135.