考虑N-1安全网络约束的输电网结构优化

张 衡，程浩忠，曾平良，张建平，陆建忠

(1． 上海交通大学 电力传输与功率变换控制教育部重点实验室，上海 200240；2． 中国电力科学研究院，北京 100192；3． 国家电网公司华东分部，上海 200002)

0 引言

受限于输电线路的物理特性，系统并不能总以发电成本最小的发电机来满足负荷需求，这就出现了输电阻塞。而可再生能源的大量并网、电力市场化改革的逐步推进，使得系统输电阻塞问题日益突出。此外，输电网的结构由规划人员按照规划目标年最大负荷需求进行设计[1]，但是在系统实际运行过程中，最大负荷往往只出现在某些特定的时段，并且持续时间比较短，这会使得系统设备利用率偏低，降低经济效益。上述问题可以通过改变系统的拓扑结构加以改善，但在电力系统运行中，电网拓扑结构的改变多集中在配电网领域[2-4]。配电网重构通过改变线路的分段开关、联络开关的状态，能够起到降低系统网损、提高供电可靠性的作用[5-6]。近年来，随着智能电网技术的发展，电力系统的运行过程更加灵活，也更加开放。从输电网角度分析，通过在运行过程中开断部分传输线路，以更加灵活的拓扑结构参与电网的调度运行，能够在降低系统阻塞费用的同时，有效地改善短路电流过大、电网电压异常等情况[7-11]。

针对输电网结构优化，已有许多学者展开了专门的研究。文献[9]将输电网结构优化模型转化成混合整数线性规划形式，该文指出，在IEEE118 测试系统中，通过对输电网结构进行优化可以降低系统25%的运行费用；文献[10]研究了输电网结构优化在降低短路电流方面的作用，而文献[11]将其作为减轻紧急事故下线路过载的控制手段；文献[12-13]将输电网结构优化运用到电力系统规划中，增强系统鲁棒性；文献[14-15]在机组组合中考虑了输电网结构优化，研究结果表明，输电网拓扑的改变会影响机组开停机方案；为了提高输电网结构优化的实用性，文献[16]将交流潮流松弛为二阶锥形式，建立了综合考虑无功和电压约束的输电网结构优化混合整数二阶锥规划模型；文献[17]采用基于序列线性规划法的启发式方法对输电网待优化线路进行排序，进而降低求解规模，并对比了不同潮流模型对优化结果的影响。

上述文献更多地是从经济性角度研究了输电网结构优化带来的经济效益，但是未对系统中的不确定因素进行量化分析。针对上述文献的不足，本文从输电网结构优化中面临的不确定因素入手，首先介绍了以降低输电阻塞为目标的输电网结构优化数学模型，给出了考虑N-1安全网络约束的结构优化模型；其次，介绍了多场景的构建方法，主要针对负荷水平以及风电场出力进行了多场景建模；再次，以修改的IEEE-RTS 24节点系统为例，对本文所提的模型和方法进行验证，并对结果进行了分析和讨论；最后，对文章进行总结并展望了未来的研究方向。

1 输电网结构优化数学模型

输电网结构优化可以看作最优潮流的扩展，因此，本文首先给出考虑最小化发电机燃料成本的直流最优潮流模型。

其中,GI为发电机集合；Cok为发电机k的单位生产费用；PG,k为发电机k的出力。

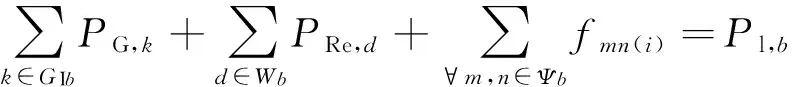
(1)

fmn(i)-rmn(i)(θm-θn)=0i∈Ω

(2)

-PLi,max≤fmn(i)≤PLi,maxi∈Ω

(3)

PG,kmin≤PG,k≤PG,kmaxk∈GI

(4)

θb,min≤θb≤θb,maxb∈Ψ

(5)

θs=0

(6)

其中，GIb为母线b处发电机集合；PRe,d为可再生能源发电机d的出力；Wb为母线b处风电场集合；fmn(i)为线路i的有功潮流，m、n为线路i两端的母线编号；Ψb表示母线b,∀m,n∈Ψb表示线路mn任意一段与母线b相连；Pl,b为母线b的负荷；rmn(i)为线路i的导纳值；θm、θn分别为母线m、n的相角；Ω为线路集合；Ψ为母线集合;PLi,max为线路i的热稳定容量；PG,kmax、PG,kmin分别为发电机k的出力上、下限；θb,max、θb,min分别为母线b相角的上、下限；θs为平衡节点相角。

式(1)表示节点功率平衡约束；式(2)表示线路潮流约束；式(3)表示线路容量约束；式(4)表示发电机出力约束；式(5)表示节点相角约束；式(6)表示平衡节点相角约束。

以li∈{0,1}表示线路i的实际运行状态，1表示正常运行，0表示断开。当线路允许开断时，则式(2)需修改为：

[fmn(i)-rmn(i)(θm-θn)]li=0

(7)

式(7)可描述为：当线路i未被断开时，线路潮流约束方程严格成立，此时约束式(2)和式(7)相同；当线路i断开时，潮流方程不再起作用。利用大M法可得式(7)的线性表示形式：

|fmn(i)-rmn(i)(θm-θn)|≤M(1-li)i∈Ω+

(8)

其中，M为较大的正数；Ω+为可被断开的线路集合。

根据上述最优潮流的描述及线路潮流方程的修改，以发电机燃料成本最小为目标，考虑N-1安全网络约束的多场景输电网结构优化模型可表示为：

(9)

(10)

(11)

(12)

(13)

(14)

(15)

li∈{0,1}i∈Ω+

(16)

(17)

θs=0

(18)

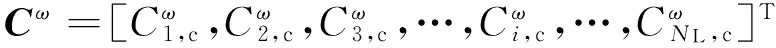
(19)

2 基于吸引子传播聚类的多场景构建

吸引子传播AP(Affinity Propagation)是一种启发式聚类算法[18]。算法基于数据的相似度矩阵，通过以欧氏距离为代表的相似度指标来对数据进行划分，从而形成不同的数据集。AP遍历所有的数据点，并将其作为潜在的聚类中心(examplar)。因此，不需要提前指定聚类的个数，是一种鲁棒性较强的聚类方法。

对任意T维数据XT=[x1,x2,…,xT]T，以负的欧氏距离表示任意2个数据点xi、xj间的相似度sij，可表示为：

sij=-‖xi-xj‖2∀i,j=1,2,…,T

(20)

则由所有T个数据组成的相似度矩阵S可由任意2点间的相似度组成，即：

(21)

当i=j时，即相似度矩阵主对角线元素被称为偏向值(preference)，以p表示。在无先验知识的情况下，如果数据点作为聚类中心的可能性相同，则以偏向值表示的主对角线元素取相同数值，通常取为所有数据点相似度的中值，即：

p=median(S(i,j))i≠j

(22)

其中，median表示对数据取中值操作。

偏向值p的大小影响最终聚类的个数，且该值越大表明该点成为聚类中心的可能性也越大。特别地，该值也可以根据实际情况设置不同的偏好值，对不同数据点赋以具有差异性的权值。此外，由于AP对相似度矩阵的对称性没有要求，在某些情况下也可以手动设置数据点间的相似度。

AP算法通过“信息交互”实现聚类，其中需要进行信息交换的2个重要参量分别是响应度(responsibility)和可用度(availability)。响应度r(i,j)代表了样本点j作为样本点i聚类中心的合适程度，而可用度a(i,j)则代表了样本点i以样本点j作为聚类中心的合适程度。

原始AP算法中对响应度和可信度的更新遵循如下的过程：

(23)

(24)

(25)

则第k次迭代后样本点i所属类中的代表点j满足：

argmaxk{a(i,j)k+r(i,j)k}

(26)

式(26)表示第k次迭代后，每一个类中的代表点j，应该满足对该类中的任意一个点i，都能够使得a(i,j)k+r(i,j)k值最大。

为了加快AP的收敛速度，避免解的振荡，引入阻尼因子λ对“信息交互”过程进行如下修改：

rk=(1-λ)rk+λrk-1

(27)

ak=(1-λ)ak+λak-1

(28)

其中，r和a分别为r(i,j)和a(i,j)的向量表示形式；λ∈[0,1]。

综上可以得出AP聚类的流程如下[19]。

a. 按照式(20)计算相似度，形成相似度矩阵S，偏向参数设为p。令k=1，对信息参量响应度r(i,j)和可用度a(i,j) 进行初始化。其中a(i,j)=0(∀i,j=1,2,…,T)，r(i,j)=sij(∀i,j=1,2,…,T)，根据式(26)求得初始聚类中心。

b. 令k=k+1，对响应度和可靠度参数进行更新：首先按(23)—(25)计算得到当前参数值，然后对当前结果与上一步迭代结果按照式(27)、(28)进行加权求和，得到最终响应度和可靠度的数值，利用式(26)更新聚类中心。

c. 判断算法是否收敛。如果不收敛，则转步骤b；如果收敛，则输出最终结果。算法的收敛依据有如下3条：算法达到最大迭代次数；聚类中心在连续迭代过程中不再发生变化；2次临近迭代结果中，响应度和可靠度变化量小于给定阈值。

3 算例分析

本文采用IEEE-RTS 24节点系统[20]，各母线负荷占总负荷的比例和发电机出力单位成本均参照文献[20-22]中的数值。以各母线负荷值为期望值，变异系数取为5 %，负荷波动服从正态分布。首先对各负荷节点进行采样，然后利用AP算法进行聚类。将500 MW线路容量降低为300 MW。为避免N-1时出现孤立节点，新增一条线路7-8，其参数与原线路相同。

在母线3、11、19上分别接入额定容量为100 MW的风电场，分别以W1、W2、W3表示。单台风机的额定功率为1 MW，切入风速Vin=3 m/s，额定风速Vr=13 m/s，切出风速Vout=25 m/s，风电场风速服从形状参数和尺度参数分别为2.73和9.6的双参数威布尔分布。对风速采样后利用AP聚类进行场景削减。

所有程序均在MATLAB上完成，模型的求解采用YALMIP[23]工具包及Gurobi[24]求解器。

3.1 基于聚类的场景设置

以风速为例分析AP算法的有效性。风速经过AP聚类后得到3个场景，如表1所示。其中，τ为该场景发生的概率。

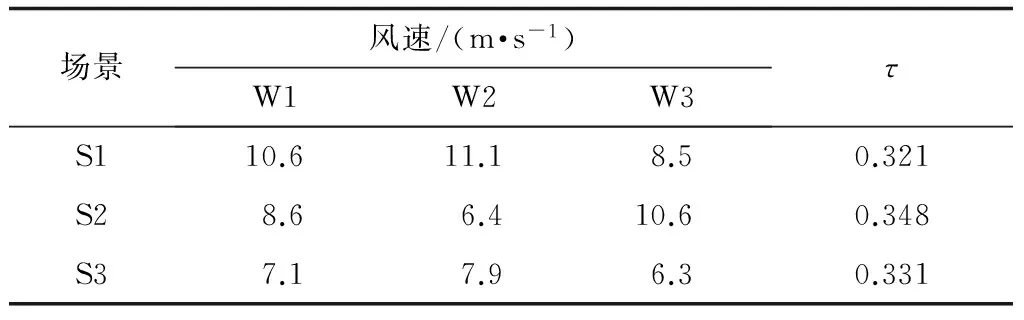
表1 风速聚类结果Table 1 Result of wind speed clustering

由于负荷数据过多，不再单独罗列。对负荷利用AP算法聚类后得到4种场景，各场景的概率如表2所示。

表2 负荷聚类结果Table 2 Result of load clustering

3.2 计算结果分析

为了更全面地反映输电网结构优化对运行费用的影响，本节设置了开断线路分别为0、1、2、3、4条这5种情况。针对直流潮流计算出的电网结构优化结果可能使得交流潮流出现无法收敛的问题，本文对考虑N-1约束的输电网结构优化结果进行了后校验。断开线路数量约束下输电网结构优化结果如表3所示，表中给出的断线方案均能使交流潮流收敛。

表3 考虑N-1安全网络约束时输电网结构优化结果Table 3 Results of OTS consideringN-1 security network constraints

从表3可以看出，仅断开一条线路10-11时，并不会出现切负荷的情况，总费用下降了5 480 $/h，下降比例达到7.66%。这是由于线路的开断会改变电网的拓扑结构，进而影响发电机出力和线路潮流分布。受网络传输容量的约束，某些运行成本较小的机组并不能够完全满发。在本算例中，当不断开线路时，母线7的100 MW机组的利用率分别达到了93.44%、94.44%和97.73%，但是其发电成本为75.64 $/(MW·h)。而发电成本较低的母线15、16的155 MW机组的利用率仅分别为35.03%和57.62%，其发电成本仅为15.46 $/(MW·h)。当断开线路10-11之后，母线7的发电机利用率下降到25%，而母线15、16的发电机利用率却分别上升到了48.32%和94.72%。因此，在断开部分线路的情况下可以降低发电成本较高的机组利用率，进而减少系统的运行费用。但当线路断开条数由2条增加到3条时，运行费用下降非常小，仅下降了1.4%，这表明继续断开输电线路并无助于降低系统的阻塞费用，而过多地断开线路将会降低系统的安全性，尤其是考虑到多重故障时，系统可靠性将会降低。

为了对比有无N-1安全网络约束对输电网结构优化的影响，本文计算了不考虑N-1约束时的输电网结构优化结果，如表4所示。

表4 不考虑N-1安全网络约束时输电网结构优化结果Table 4 Results of OTS without consideringN-1 security network constraints

对比表3和表4可以看出，考虑N-1安全网络约束与否对输电网结构优化的结果有很大的影响。在同样断开线路数量约束的前提下，两者的开断线路并不相同。虽然不考虑N-1约束时输电网结构优化能够更有效地降低系统的阻塞，但是当断开线路达到3条及以上时，会出现交流潮流无法收敛的情况。

为了比较不同开断线路情况下线路的负载率水平，本文以线路平均负载率为指标，其计算公式如下。

线路负载率：

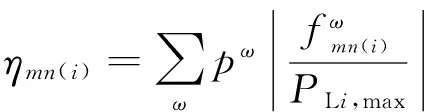
(29)

平均负载率：

ηave=mean(ηmn) ∀m,n∈Ω

(30)

其中，mean表示取均值操作。

不同开断线路条数下输电线路负载率如表5所示。根据表3和表5可以看出，随着线路断开条数的增加，系统输电阻塞下降的同时，提高了线路的平均负载率水平，使得线路整体利用率得以提高。

表5 不同开断线路条数下的输电线路负载率Table 5 Transmission line load rate fordifferent numbers of lines switched off

3.3 风电场容量对输电网结构优化的影响

当前可再生能源大量并网，其出力的随机性和间歇性会影响电网的稳定运行。因此，本节研究不同风电场容量对输电网结构优化的影响。共设置了风电场容量为50 MW、150 MW、200 MW这3个场景，优化结果如表6所示。

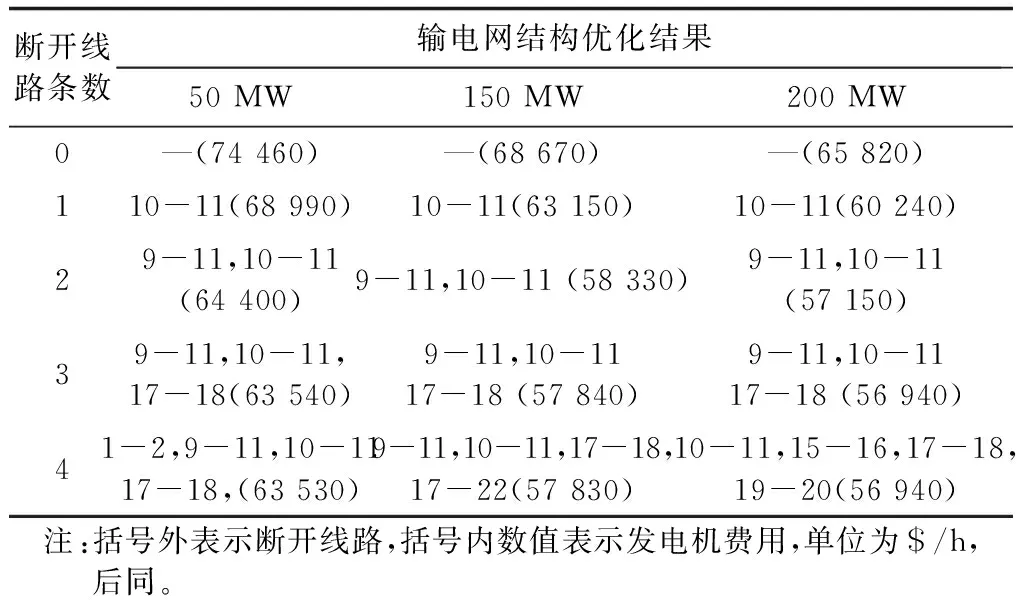
表6 不同风电场容量下的输电网结构优化结果Table 6 Results of OTS for different capacities of wind farms

由表6可以看出，风电场的接入会降低系统的燃料成本，并且其随着风电场容量的增大而下降。风电出力虽然具有波动性，但仍然具有一定的置信度，能够代替一部分常规机组，从而降低系统的生产成本。在本算例中，风电场容量的变化主要影响母线13、15、16的发电机出力，以断开线路10-11为例，当风电场容量由50 MW增加到200 MW时，母线13上发电机平均利用率由62.4%下降到43.3%，而其余母线的发电机利用率分别下降了6%和8%。从输电网结构优化的结果可以看出，风电场容量对输电网结构优化的影响主要体现在断开线路数量较多时。在本文算例中，只有当断线数量达到4条时，输电网结构优化的结果才会出现差别，但断开如此数量的线路对降低系统阻塞作用已经很小。

3.4 线路传输容量对输电网结构优化的影响

输电网结构优化的本质是为了消除由于线路传输容量的约束导致的系统输电阻塞。因此，本节分析了不同系统阻塞程度对输电网结构优化的影响。将原系统中容量为500 MW的线路分别换为250 MW、350 MW、400 MW、450 MW这4种计算场景，分别计算在相应线路传输容量下的输电网结构优化，计算结果如表7所示。

表7 不同线路容量下的输电网结构优化结果Table 7 Results of OTS for different capacities of lines

根据表3和表7可以看出，不同输电线路容量下，系统的阻塞程度不同。当输电线路容量从250 MW上升到400 MW时，系统的燃料费用由80 030 $/h下降到了60 010 $/h。而线路容量继续增加至450 MW时，系统的燃料成本不再增加，即此时系统不再有阻塞存在。对比不同线路容量下的输电网结构优化结果，当线路存在阻塞且只允许断开一条输电线路时，前3种场景下的输电网结构优化结果相同，均为断开线路10-11，而当线路容量达到400 MW时，断开线路变为18-21。随着输电线路容量的增加，输电阻塞已得到消除，但通过断开线路可以提高负载率水平。在本算例中，线路容量到400 MW、450 MW时，负载率分别由35.63%、33.33%上升到36.14%和34.09%。另一方面，随着阻塞程度的降低，开断更多线路时，系统燃料费用不再降低。当线路传输容量达到350 MW时，仅仅断开10-11 能够降低系统的阻塞，继续开断线路，并不会进一步降低系统的燃料成本。而当线路容量大于400 MW时，系统不存在输电阻塞，此时断开线路不会降低系统的运行成本。

3.5 结果对不确定因素的适应性

由于本文使用的是直流潮流，所以从有功平衡的角度验证所提模型在应对不确定因素时的适应性。首先，采用蒙特卡洛模拟法对负荷和风速进行采样，采样规模为10 000次，然后对系统状态进行校正，计算切负荷量。当负荷、风电波动时系统的切负荷量如表8所示。

表8 不同断开线路条数下的系统平均切负荷量Table 8 System average load shedding fordifferent numbers of lines switched off

根据表8可以看出，断开部分输电线路时，系统在负荷、风电波动时的线路过载程度变化很小。即便是断开4条线路，其平均切负荷量仅有5.6 MW。在断开1条线路10-11时，与不断开线路的切负荷量相同，均为0。

为了进一步验证模型对输电线路发生随机故障时的适应性，本文从有功功率平衡的角度对断开不同线路条数时考虑输电线路发生随机故障的系统可靠性进行评估。以系统平均切负荷量、切负荷概率和系统状态校正不收敛次数3个指标来表征系统的适应性。为了简单起见，每条线路的强迫停运率取均为0.05，且线路只有正常运行和停运2种状态，由于多重故障发生的概率非常小，本文在采样过程中最多考虑2重线路故障。仍然采用蒙特卡洛模拟对线路状态进行采样，结果如表9所示。

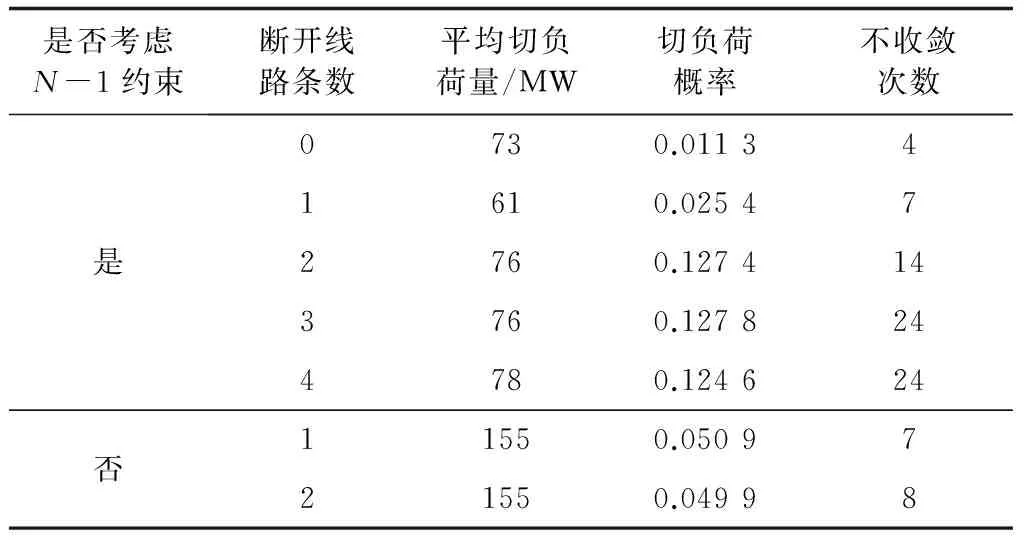
表9 考虑线路随机故障时断开不同线路系统各项指标Table 9 System indexes considering stochastic faults oftransmission lines for different numbers of lines switched off

不断开线路时，由于系统线路拥有更多的传输容量，发生多重故障后，出现切负荷和最优潮流不收敛的概率最低。虽然此时系统的平均切负荷量不是最少，但在所有采样场景下的总切负荷量为8 249 MW，在其他断开不同输电线路的计算场景中最低。断开线路10-11时，系统切负荷概率和最优潮流不收敛次数有所增加，但系统的平均切负荷量出现了下降。通过对系统拓扑结构的优化，改善了线路潮流分布，在降低阻塞发生的同时减少了系统的平均切负荷量。随着开断线路数量的增加，系统的切负荷概率出现了大幅增长。因此，输电网结构优化虽然有助于降低系统的阻塞成本，但是开断线路不宜过多，否则会极大地降低系统的可靠性水平。

对比表3、4、10可以看出，不考虑N-1约束时，断开线路11-14能够更有效地降低系统阻塞，使得发电机费用下降了14%。但在对可靠性的计算中，与考虑N-1约束相比，其切负荷概率提高了2倍。因此，根据以上计算结果可以看出，考虑N-1约束与否对系统的拓扑优化具有很重要的影响。

4 结论

随着智能电网的发展，未来输电网将变得更加开放，其网络拓扑结构也就会以更加灵活的方法参与到系统的运行中。为了研究输电网拓扑结构不变化对降低系统阻塞的作用,本文建立了考虑N-1安全网络约束的输电网结构优化模型，采用多场景技术考虑了负荷波动以及风电出力不确定性对输电网拓扑优化的影响。通过对算例的分析，得到如下结论。

a. 对于有输电阻塞的系统，可以通过断开部分线路以减轻系统阻塞、降低运行成本，但过多断开线路并不能更有效地降低阻塞，反而会使得系统的可靠性水平下降。

b. 是否考虑N-1安全网络约束会影响输电网结构优化的结果。不考虑N-1约束时，断开一条输电线路能够更有效地降低系统的阻塞，但是系统可靠性水平下降较明显。

c. 风电场出力虽然具有一定的波动性和随机性，但风电具有一定的置信度，能够代替一部分常规电源，降低系统的运行费用。但在本文算例中，风电场容量的变化对输电网结构优化影响较小，仅在断线数量达到4条时才会出现不同。

输电网结构优化对系统的影响体现在多方面，未来对输电网结构优化的研究还将集中在降低系统短路电流，考虑多重故障的场景削减技术，以及对系统经济调度、输电线路及发电机组检修等的影响。

参考文献：

[ 1 ] 程浩忠. 电力系统规划[M]. 北京：中国电力出版社,2014:5-33.

[ 2 ] 吉兴全,刘琪,于永进. 基于功率矩和邻域搜索的有源配电网两层重构算法[J]. 电力自动化设备,2017,37(1):28-34.

JI Xingquan,LIU Qi,YU Yongjin. Two-level reconfiguration algorithm based on power moment and neighbourhood searching for distribution network[J]. Electric Power Automation Equipment,2017,37(1):28-34.

[ 3 ] 王薪苹,卫志农,孙国强,等. 计及分布式电源和负荷不确定性的多目标配网重构[J]. 电力自动化设备,2016,36(6):116-121.

WANG Xinping,WEI Zhinong,SUN Guoqiang,et al. Multi-objective distribution network reconfiguration considering uncertainties of distributed generation and load[J]. Electric Power Automation Equipment,2016,36(6):116-121.

[ 4 ] 李春燕,杨强,魏蔚,等. 计及风速与负荷相关性的配电网重构方法[J]. 电力自动化设备,2016,36(2):148-153.

LI Chunyan,YANG Qiang,WEI Wei,et al. Distribution network reconfiguration considering correlation between wind-speed and load[J]. Electric Power Automation Equipment,2016,36(2):148-153.

[ 5 ] BAHADOORSINGH S,MILANOVIC J V,ZHANG Y,et al. Minimization of voltage sag costs by optimal reconfiguration of distribution network using genetic algorithms[J]. IEEE Transactions on Power Delivery,2007,22(4):2271-2278.

[ 6 ] MENDES A,BOLAND N,GUINEY P,et al. Switch and tap-changer reconfiguration of distribution networks using evolutionary algorithms[J]. IEEE Transactions on Power Systems,2013,28(1):85-92.

[ 7 ] ROLIM J G,MACHADO L J B. A study of the use of corrective switching in transmission systems[J]. IEEE Transactions on Power Systems,1999,14(1):336-341.

[ 8 ] 杨知方,钟海旺,夏清,等. 输电网结构优化问题研究综述和展望[J]. 中国电机工程学报,2016,36(2):426-434.

YANG Zhifang,ZHONG Haiwang,XIA Qing,et al. Review and prospect of transmission topology optimization[J]. Proceedings of the CSEE,2016,36(2):426-434.

[ 9 ] FISHER E B,NEILL R P O,FERRIS M C. Optimal transmission switching[J]. IEEE Transactions on Power Systems,2008,23(3):1346-1355.

[10] YANG Z,ZHONG H,XIA Q，et al. Optimal transmission switching with short-circuit current limitation constraints[J]. IEEE Transactions on Power Systems,2016,31(2):1278-1288.

[11] MAZI A A,WOLLENBERG B F,HESSE M H. Corrective control of power system flows by line and bus-bar switching[J]. IEEE Tran-sactions on Power Systems,1986,1(3):258-264.

[12] DEHGHAN S，AMJADY N. Robust Transmission and energy storage expansion planning in wind farm-integrated power systems conside-ring transmission switching[J]. IEEE Transactions on Sustainable Energy,2016,7(2):765-774.

[13] VILLUMSENJ C,BRØNMO G，PHILPOTT A B. Line capacity expansion and transmission switching in power systems with large-scale wind power[J]. IEEE Transactions on Power Systems,2013,28(2):731-739.

[14] HEDMANK W,FERRIS M C,O’NEILL R P,et al. Co-optimization of generation unit commitment and transmission switching withN-1 reliability[J]. IEEE Transactions on Power Systems,2010,25(2):1052-1063.

[15] KHODAEI A,SHAHIDEHPOUR M. Transmission switching in security-constrained unit commitment[J]. IEEE Transactions on Power Systems,2010,25(4):1937-1945.

[16] BAI Y,ZHONG H,XIA Q，et al. A conic programming approach to optimal transmission switching considering reactive power and voltage security[C]∥2015 IEEE Power & Energy Society General Meeting. Denver,CO,USA：[s.n.]，2015：1-5.

[17] SOROUSH M，FULLER J D. Accuracies of optimal transmission switching heuristics based on DCOPF and ACOPF[J]. IEEE Transactions on Power Systems,2014,29(2): 924-932.

[18] FREY B J,DUECK D. Clustering by passing messages between data points[J]. Science,2007,315(5814):972-976.

[19] 周琼,贠志皓,丰颖,等. 风电接入下基于AP聚类的无功功率-电压控制分区方法[J]. 电力系统自动化,2016,40(13):19-27.

ZHOU Qiong,YUN Zhihao,FENG Ying,et al. Reactive power-vol-tage control partitioning of wind power integration system based on affinity propagation clustering[J]. Automation of Electric Power Systems,2016,40(13):19-27.

[20] GRIGG C. The IEEE Reliability Test System-1996. A report prepared by the reliability test system task force of the application of probability methods subcommittee[J]. IEEE Transactions on Power Systems,1999,14(3):1010-1020.

[21] HENNEAUX P，KIRSCHEN D S. Probabilistic security analysis of optimal transmission switching[J]. IEEE Transactions on Power Systems,2016,31(1):508-517.

[22] ORFANOSG A,GEORGILAKIS P S，HATZIARGYRIOU N D. Transmission expansion planning of systems with increasing wind power integration[J]. IEEE Transactions on Power Systems,2013,28(2):1355-1362.

[23] LOFBERG J. YALMIP: a toolbox for modeling and optimization in MATLAB[C]∥IEEE International Symposium on Computer Aided Control Systems Design. Taiwan,China：[s.n.]，2004:284-289.

[24] Gurobi Optimization,Inc. Gurobi optimizer reference manual[EB/OL].[2016-11-15]. http:∥www.gurobi.com.