计及噪声的动态谐波准同步采样分析方法

朱 亮，温 和，戴慧芳，赵震宇，张春强

(1. 国网江西省电力有限公司电力科学研究院，江西 南昌 330096；2. 湖南大学 电气与信息工程学院，湖南 长沙 410082)

0 引言

电力系统谐波的准确测量为电能计量、电能质量分析、故障诊断以及电力谐波抑制与补偿等提供科学依据[1-3]。通过对谐波的检测，可以计算各次谐波含量以及谐波电压与电流的频率、相位、幅值参数[4]。由于谐波具有非线性、随机性、分布性、非平稳性等特征，难以对谐波进行准确测量[5]。

现有的动态谐波测量算法中，主要有基于傅里叶变换的谐波测量方法、基于瞬时无功功率的谐波测量方法、基于小波变换的谐波测量方法、基于现代谱估计的谐波测量方法[6-10]。虽然这些方法已经在实际设备中得到应用，但都存在一些不足。

基于傅里叶变换的谐波测量方法是当今应用最广泛的一种方法。该算法的可靠性、稳定性较高，并有快速傅里叶变换(FFT)算法可以提高信号检测的实时性，测量精度高，实现简单，且被IEC61000-4-7标准采用。该算法的缺点是需要一定时间的采样值，且需要进行2次变换，计算量大；而且当测量周期不等于信号周期的整数倍或对信号进行截断时，FFT算法会产生频谱泄漏和栅栏效应，引起较大的误差。在减少频谱泄漏方面，对FFT加窗是应用比较广泛的方法[11-13]。加窗FFT算法分析谐波遇到的主要问题是同步偏差及初始相位敏感性，即源于非整数周期采样和采样初始时刻的随机性。而实际应用中，无法严格做到同步采样[14-15]。选用旁瓣峰值电平高于-58 dB的窗函数分析电网谐波时，取5个基波周期作为时域分析长度，就可以忽略初始相位敏感性。

基于瞬时无功功率的谐波测量方法的核心在于经过不含零序分量的Park变换得到三相电流。当电网电压对称且无畸变时，各电流分量的测量电路比较简单并且延时小。但该算法需要2次坐标变换，计算量较大，且目前常采用IIR滤波器，跟随性能不好。通过采用高阶滤波器或提高截止频率可提高暂态响应速度，但谐波检测准确度会相应降低。基于小波变换的谐波测量方法以周期信号模型为基础，通过频率分析进行频率测量。该算法计算精度高，能分析稳态信号，也能分析暂态时变信号，但是小波变换频带划分不绝对，可能产生频带重叠，同时由于能量不集中，易产生频谱泄漏，导致谐波分析准确度降低[16-18]。基于现代谱估计的谐波测量方法通过建立模拟实际过程的模型，利用测量数据来估计该模型的参数，最后利用有限的数据对信号模型的参数进行估计。但当信号模型中含有噪声时，分辨率就会降低，同时构造样本函数计算量偏大，实现也较复杂。实际测量中，一方面根据微小误差准则，算法可能引入的随机误差和系统误差，影响谐波测量精度；另一方面弱幅值的谐波往往容易被邻近的强频率成分干扰，这也对算法的精度提出了更高要求。因此，研究高精度的谐波分析算法对动态谐波测量具有重要的意义。

20世纪80年代，东南大学的戴先中教授提出准同步采样算法QSSA(Quasi-Synchronous Sampling Algorithm)[19-20]。该算法的提出使非同步采样情况下的频率测量精度得到了明显改善，这正是由于QSSA不要求满足严格的同步采样条件，即允许存在一定的采样同步偏差。QSSA在电力系统频率测量和谐波分析中得到了广泛的应用。实际应用中，谐波分析准确度往往受到噪声影响，而噪声影响下的准同步采样谐波分析的准确度问题还有待深入研究。

本文提出一种基于QSSA的动态谐波分析算法，分析噪声对谐波频率测量的影响，建立了谐波频率测量方差理论式。仿真与实际应用结果表明基于QSSA的动态谐波算法能克服频率波动及噪声影响，实现较高精度的动态谐波测量。

1 动态谐波的准同步采样分析算法

QSSA不要求采样周期与信号周期严格同步，对采样起点没有要求。

根据文献[21]和[22]，含谐波的信号的模型可设为：

(1)

其中，T为信号周期；f0为基波频率，第h次谐波的频率为fh=hf0；Ah为第h次谐波的幅值；φh为第h次谐波的初相角；H为最高谐波次数。

设x(t)为被积函数，[a，b]为积分区间，则利用复化梯形公式获得的数值积分结果为：

(2)

其中，N为序列长度；d=(b-a)/N为归一化积分步长；ti=a+id(i=0，1，…，N)为积分点；x(a)与x(b)为所求区间两端处的函数值。复化梯形积分的权值如表1所示，表中ρ为由数值积分公式和N所确定的权系数。

表1 复化梯形积分的权值Table 1 Weight of complex trapezoidal integral

以采样频率fs=1/Ts对x(t)进行采样，从采样序列中提取长度为LN+1的采样序列x(n)(n∈[1，LN+1])，其中Ts为采样周期，L为迭代次数。

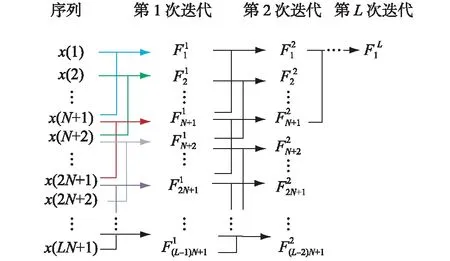
图1 准同步采样的L次迭代Fig.1 Lth iteration process based on QSSA

准同步采样的L次迭代的原理如图1所示。运用式(2)对采样序列x(n)数值积分公式作图1所示的递推运算，得到递推运算结果为：

(3)

其中，i=1，2，…，(l-1)N+1为在运用式(3)计算平均值过程中各子区间序号；ρn(n=i，i+1，…，i+N)为由数值积分公式和N所确定的权系数；l=1，2，…，L为迭代次数。根据离散傅里叶变换的定义，x(m)的离散频谱的实部和虚部可以按照式(3)分别进行L次迭代。

如图2所示，从准同步采样序列中提取长度为LN+1的序列x1(m)，即(x1(m0)，x1(m0+1)，…，x1(m0+LN))，其起始时刻为t0=m0/fs，m0为对应起始时刻的正整数值。对于第h次谐波，序列x1(m)的初始相角为ϑt0=2πfhm0/fs+φ。

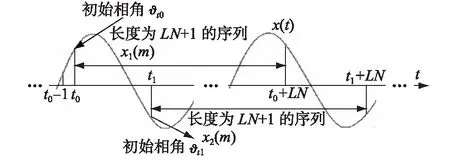
图2 序列选取示意图Fig.2 Schematic diagram of sequence selection

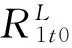
(4)

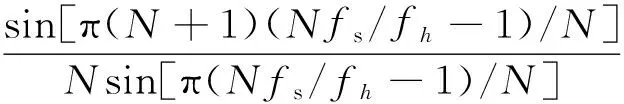
(5)

其中，γmm为迭代因子。

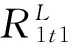
(6)

用ϑt0减去ϑt1，即可计算第h次谐波的频率为：

(7)

根据式(4)，第h次谐波的幅值与初始相角分别为：

(8)

(9)

2 噪声对动态谐波频率测量的影响分析

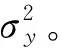
(10)

(11)

其中，ϑm0和ϑm1分别为第m0和m1采样点对应的初始相角。

同理，由式(6)可得ϑm0减去ϑm1的方差理论计算式分别为：

(12)

(13)

其中，k=fhN/fs。将式(11)和(12)代入式(10)，可得：

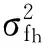
(14)

其中，2σy2/A2即为信噪比SNR的倒数。

式(14)表明，谐波频率测量的方差与信噪比成反比，即信号越弱(对应的噪声越强)，频率测量方差越大。此外，式(14)还可以用于确定频率测量过程中的各项参数。如果给定了频率测量误差的限值，对于已经完成采样的信号序列，可以通过式(14)计算出采用QSSA所需的最小序列长度N和迭代次数L。比如，给定频率测量的极限误差为0.002(按2倍标准差分析)，则频率测量方差限值为10-6，设采样频率为6 400 Hz，测量通道信噪比为10 dB，代入式(14)可计算得到：当N取256时，L至少取值为4。在实际测量中，可以运用式(14)确定频率测量过程中的采样频率fs、序列长度N和迭代次数L，以满足预设的频率测量误差限值。

3 动态谐波仿真分析

对于提出的基于QSSA的动态谐波分析方法，通过MATLAB仿真实验来验证该分析方法的可行性和有效性。

3.1 含基波和2～21次谐波信号仿真实验

设包含基波和2～21次谐波的信号表达式为：

(15)

其中，基波频率f0为50.1 Hz；采样频率为6 400 Hz。Ah和φh具体取值见表2。基于QSSA的动态谐波分析 方法以及基于4项3阶Nuttall窗插值FFT、Hanning窗插值FFT和Hamming窗插值FFT对基波频率、2～21次谐波频率测量的绝对误差分布图如图3(a)所示。所有算法均使用1 024个采样点。

由图3(a)可知，基于QSSA的动态谐波分析算法对基波及各次谐波的频率测量绝对误差均小于10-10Hz，且频率绝对误差的准确度远远高于基于4项3阶Nuttall窗插值FFT、Hanning窗插值FFT和Hamming窗插值FFT，准确度比加窗插值FFT算法高6～7个数量级。基于QSSA的动态谐波分析方法和基于4项3阶Nuttall窗插值FFT、Hanning窗插值FFT和Hamming窗插值FFT相角测量绝度误差和幅值测量相对误差的分布曲线分别如图3(b)、(c)所示。

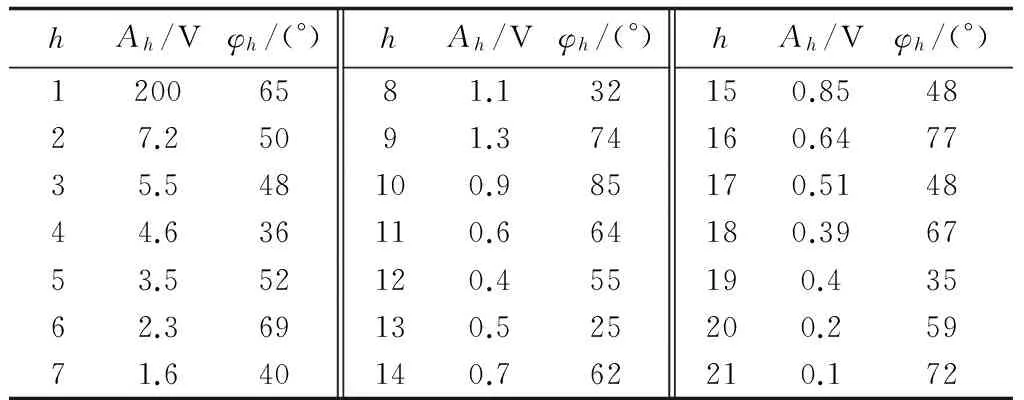
表2 基波及谐波参数Table 2 Parameters of fundamental and harmonic waves

图3 基波和谐波测量误差Fig.3 Measurement errors of fundamental and harmonic waves

由图3(b)、(c)可知，基于QSSA的动态谐波分析算法的相角测量和幅值测量的准确度远远高于基于4项3阶Nuttall窗插值FFT、Hanning窗插值FFT和Hamming窗插值FFT，准确度分别比WIFFT算法高6～7和7～8个数量级。完全满足国标相角偏差小于±5°的要求。

3.2 不含白噪声时频率波动仿真实验

基波频率波动时，将引起信号各频率分量之间的频谱泄漏量发生变化，影响各参数检测的准确度。为了分析信号频率波动对基波及各次谐波的幅值和相角的影响，基波频率f0分别在49.5～50.5 Hz内取值，步长为0.1 Hz。在此条件下，对式(15)所示信号进行仿真分析。图4为基波频率波动时，基于QSSA的动态谐波分析算法频率测量绝对误差、相角测量绝对误差和幅值测量相对误差的分布曲线图。

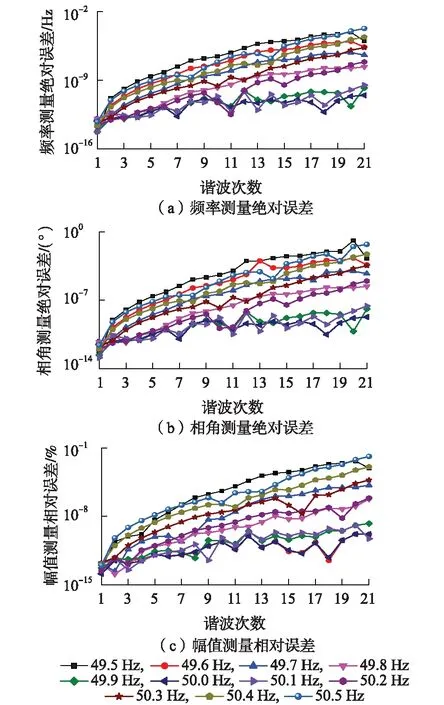
图4 基波频率波动时基波和谐波测量误差Fig.4 Measurement errors of fundamental and harmonic waves when fundamental wave frequency fluctuates

由图4(a)可知，基波频率f0=49.5 Hz时，基于QSSA的动态谐波分析算法准确度最低，但基波及各次谐波频率测量绝对误差仍小于10-3Hz。当频率越靠近50 Hz，基波及各次谐波的误差越小。实行严格的同步采样，当f0=50 Hz时，基波及2～21次谐波频率测量绝对误差非常小，频率测量绝对误差可以达到10-14～10-11Hz。

由图4(b)可知，实行严格的同步采样，当f0=50 Hz时，基波及2～21次谐波相角测量绝对误差非常小，相角测量绝对误差可以达到10-12°～10-9°。当基波频率f0在49.5～49.9 Hz和50.1～50.5 Hz范围内波动时，相角测量绝对误差波动比较大，但均小于0.1°。

由图4(c)可知，实行严格的同步采样，当f0=50 Hz时，基波及2～21次谐波幅值测量相对误差非常小，谐波测量幅值相对误差可以达到10-14%～10-10%。当基波频率越远离50 Hz时，幅值相对误差越来越大。当基波频率f0在49.5～49.9 Hz和50.1～50.5 Hz范围内波动时，幅值测量相对误差在10-6%～10-3%范围内波动。

3.3 白噪声影响下谐波仿真实验

在实际测量中，不可避免地会受到外界噪声的干扰(主要是电磁干扰)，因此对式(15)所示的信号添加高斯白噪声，高斯白噪声的信噪比为50 dB。通过仿真对添加高斯白噪声时基于QSSA的动态谐波分析算法与加窗插值FFT算法对谐波测量的结果进行对比分析，在同一信噪比下计算500次频率、相角和幅值，其余仿真参数不变。图5给出了信号添加白噪声时频率、相角和幅值测量方差。

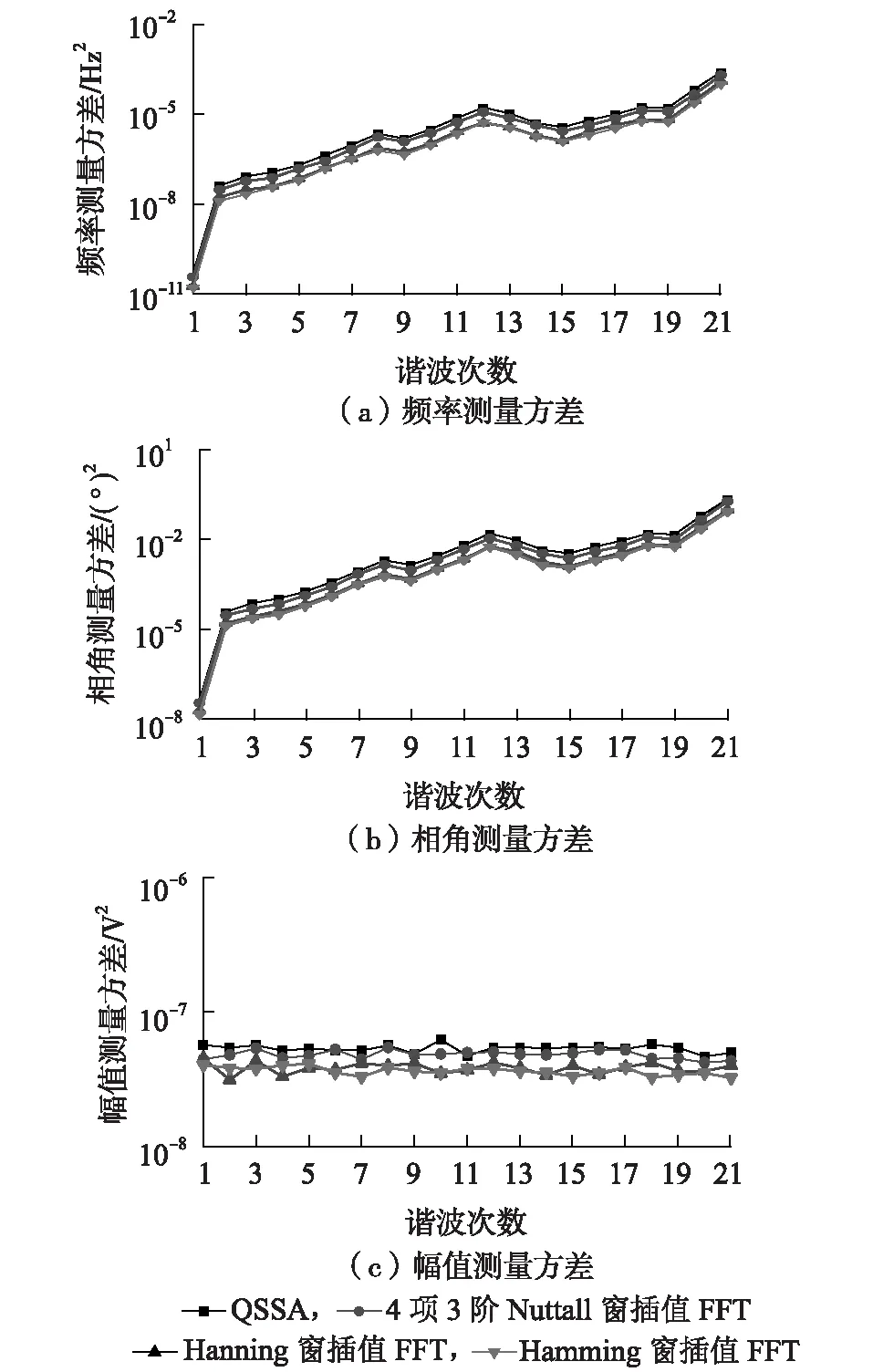
图5 50 dB白噪声时基波和谐波测量方差Fig.5 Measurement variance of fundamental and harmonic waves in 50 dB white noise

由图5可知，基于QSSA的动态谐波分析算法的频率方差、相角方差和幅值方差与加窗插值FFT算法在同一等级，且方差都比较小，幅值方差的波动均在10-8～10-7范围内。因此，基于QSSA的动态谐波分析算法可有效克服噪声的影响，能准确测量基波及各次谐波的幅值。

根据算法实现流程，长度为N的QSSA所需的加法和乘法次数分别为L2N和LN/2+LN2/2+L+1，而加窗插值FFT算法所需要的加法和乘法次数分别为3(LN+1)log2(LN+1)和2(LN+1)log2(LN+1)。可见，QSSA的运算量略大于加窗插值FFT算法。图5的仿真结果表明：QSSA与加窗插值FFT算法具有相同数量级的谐波测量方差。但值得注意的是，如图3所示，前者的谐波测量绝对误差优于后者约6～7个数量级。

4 应用与讨论

为了验证基于QSSA的动态谐波分析方法在实际应用中的可靠性，本文开展了动态谐波测量实验。实验平台由三相标准源HBS1030、数据采集卡NI-ELVIS(Ⅱ)、电压预处理电路板(目的是为了降压)以及上位机LenovoY460组成。三相标准源HBS1030的最高输出谐波频率为6 kHz，输出频率稳定度为5×10-5；数据采集卡NI-ELVIS(Ⅱ)的ADC分辨率为16位，最大采样频率为1.25 MHz，电压输入范围为0～10 V。

三项标准源通电后，首先通过标准源的前面板设置输出信号的频率、幅值、谐波次数与谐波含有率等，其中，基波频率设为50.5 Hz，基波和谐波的幅值设置如表2所示，基波和谐波的初相角均设为0；然后将标准源设置完成的电信号送至电压预处理电路模块，将电压幅值降至5 V左右；之后将降压之后的电信号送入数据采集卡NI-ELVIS(Ⅱ)的信号输入端口，NI-ELVIS(Ⅱ)的电压输入范围为0～10 V，NI-ELVIS(Ⅱ)的采样频率可以通过上位机设置，在本实验中，采样频率设置为fs=6.4 kHz；最后，将采集到的数据送入上位机LenovoY460进行波形及数据的存储。

在实际测量实验中，存在很多因素导致测量结果出现随机偏差。比如，标准信号源输出的不稳定性、互感器受到的电磁干扰、预处理和采样电路的电子热噪声、模数转换器的量化误差、计算过程中的截断误差等，这些因素都会导致谐波测量结果无规则地偏离真实值，均可以视为一定水平的白噪声影响。因此，在本文的实际测量实验中，未对标准源产生的信号添加额外的白噪声。

图6为实际测量实验的基波和谐波频率、幅值和初相角的绝对误差和方差。实际测量结果表明，本文所提出的算法在基波频率、幅值和初相角测量时具有很高的精度，但当谐波次数较高时，误差有所增加。特别值得注意的是，图6中，谐波幅值的绝对误差小于10-4V，方差小于10-6V2，完全满足国标GB/T 17626.7—2008《供电系统及所连设备谐波、谐间波的测量和测量仪器导则》中A类测量准确度的要求。

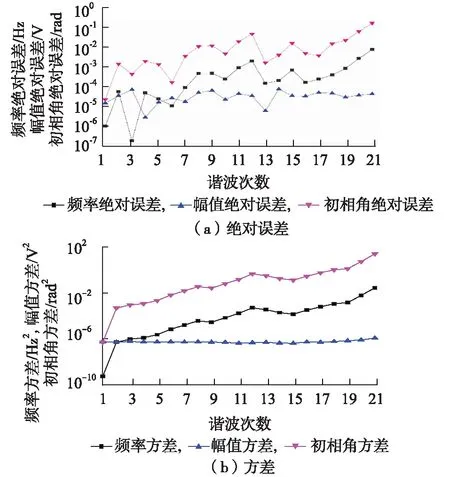
图6 实际测量实验基波和谐波的绝对误差和方差Fig.6 Absolute errors and variances of fundamental and harmonic waves in practical measurement experiment

5 结论

本文提出了基于QSSA的动态谐波分析算法，分析了噪声对谐波频率测量的影响，建立了谐波频率测量方差理论式。研究结果表明，谐波频率测量的方差与信噪比成反比，即信号越弱(对应的噪声越强)，频率测量方差越大。此外，式(14)中，频率测量方差受到采样频率fs、序列长度N和迭代次数L等影响，为合理选择上述参数达到合理的谐波频率测量方差水平提供了理论依据。基波频率波动、白噪声等情况下的仿真和实际测量实验验证了本文所提算法的准确度。

参考文献：

[ 1 ] 李宁，左培丽，王新刚，等. 基于改进DFT和时域准同步的间谐波检测算法[J]. 电力自动化设备,2017,37(4):170-178.

LI Ning，ZUO Peili，WANG Xingang，et al. Inter-harmonic detection based on improved DFT and time-domain quasi-synchronization[J]. Electric Power Automation Equipment，2017,37(4):170-178.

[ 2 ] 柳永妍，乐健，李琼林，等. 电容式电压互感器谐波测量误差研究[J]. 电力自动化设备,2017,37(3):167-174.

LIU Yongyan，LE Jian，LI Qionglin，et al. Research on harmonic measurement error of CVT[J]. Electric Power Automation Equipment,2017,37(3):167-174.

[ 3 ] 方志聪. 基于FFT变换的电网谐波分析及其仿真研究[J]. 电气应用,2014,33(4):68-71.

FANG Zhicong. Grid harmonic analysis and simulation based on the FFT[J]. Electrotechnical Application,2014,33(4):68-71.

[ 4 ] 吴超凡，陈隆道. 基于分段插值同步化算法的谐波测量[J]. 电力系统保护与控制，2016,44(9):1-6.

WU Chaofan,CHEN Longdao. Harmonic measurement based on piecewise interpolation synchronization algorithm[J]. Power System Protection and Control,2016,44(9):1-6.

[ 5 ] BARROS J，DIEGO R I，DE APRAIZ M. Applications of wavelet transform for analysis of harmonic distortion in power systems:a review[J]. IEEE Transactions on Instrumentation and Measurement，2012，61(10):2604-2611.

[ 6 ] JAIN S K，SINGH S N. Low-order dominant harmonic estimation using adaptive wavelet neural network[J]. IEEE Transactions on Industrial Electronics，2014，61(1):428-435.

[ 7 ] 陈静，符玲，臧天磊，等. 考虑系统谐波阻抗改变的谐波责任定量划分方法[J]. 电力自动化设备,2016,36(6):215-222.

CHEN Jing，FU Ling，ZANG Tianlei，et al. Harmonic contribution determination considering system harmonic impedance change[J]. Electric Power Automation Equipment，2016，36(6):215-222.

[ 8 ] 李亚琼，周胜军，王同勋，等. 基于优选带宽核密度估计的谐波概率潮流分析方法[J]. 电力自动化设备,2017,37(8):131-136.

LI Yaqiong，ZHOU Shengjun，WANG Tongxun，et al. Harmonic pro-babilistic power-flow analysis based on kernel density estimation with optimized bandwidth design[J]. Electric Power Automation Equipment，2017，37(8):131-136.

[ 9 ] TIWARI V K，JAIN S K. Hardware implementation of polyphase-decomposition-based wavelet filters for power system harmonics estimation[J]. IEEE Transactions on Instrumentation and Measurement，2016，65(7):1585-1595.

[10] 汪飞，毛华龙，许德志，等. 多变电网条件下的对称序列与谐波检测[J]. 电工技术学报，2014，29(12)：158-165.

WANG Fei，MAO Hualong，XU Dezhi，et al. Symmetrical sequence and harmo-nic detection in varied grid conditions[J]. Transactions of China Electrotechnical Society，2014，29(12):158-165.

[11] 蔡涛，段善旭，刘方锐. 基于实值MUSIC算法的电力谐波分析方法[J]. 电工技术学报，2009，24(12):149-155.

CAI Tao，DUAN Shanxu，LIU Fangrui. Power harmonic analysis based on real-valued spectral MUSIC algorithm[J]. Transactions of China Electrotechnical Society，2009，24(12):149-155.

[12] 潘文，钱俞寿，周鹗. 基于加窗插值FFT的电力谐波测量理论(Ⅱ)双插值FFT理论[J]. 电工技术学报，1994，9(2)：53-56.

PAN Wen，QIAN Yushou，ZHOU E. Power harmonies measurement based on windows and interpolated FFT(Ⅱ) dual interpolated FFT algorithms[J]. Transactions of China Electrotechnical Society，1994，9(2)：53-56.

[13] 温和,滕召胜,王永,等. 改进加窗插值FFT动态谐波分析算法及应用[J]. 电工技术学报,2012,27(12)：270-277.

WEN He，TENG Zhaosheng，WANG Yong，et al. Improved windowed interpolation FFT algorithm and application for power harmonic ana-lysis[J]. Transactions of China Electrotechnical Society，2012,27(12)：270-277.

[14] 曾博,滕召胜,周毅波. 改进FFT非稳态电力谐波分析及应用[J]. 电工技术学报,2012,27(11):256-262.

ZENG Bo，TENG Zhaosheng，ZHOU Yibo. Power system harmonic analysis under nonstationary situations and its application based on improved FFT method[J]. Transactions of China Electrotechnical Society，2012,27(11):256-262.

[15] WEN H，ZHANG J，MENG Z，et al. Harmonic estimation using symmetrical interpolation FFT based on triangular self-convolution window[J]. IEEE Transactions on Industrial Informatics，2015，11(1):16-26.

[16] TARASIUK T. Hybrid wavelet & ndash;Fourier method for harmo-nics and harmonic subgroups measurement & mdash;case study[J]. IEEE Transactions on Power Delivery，2007，22(1):4-17.

[17] PAK L F，DINAVAHI V，CHANG G，et al. Real-time digital time-varying harmonic modeling and simulation techniques IEEE task force on harmonics modeling and simulation[J]. IEEE Transactions on Power Delivery，2007，22(2):1218-1227.

[18] EREN L，UNAL M，DEVANEY M J. Harmonic analysis via wavelet packet decomposition using special elliptic half-band filters[J]. IEEE Transactions on Instrumentation and Measurement，2007，56(6):2289-2293.

[19] 沈国峰，王祁，张世平，等. 电力交流参数测量中非均匀采样问题的误差分析[J]. 仪器仪表学报，2003，24(4)：512-514.

SHEN Guofeng，WANG Qi，ZHANG Shiping，et al. Error analysis on non-uniformly sampling of power system AC parameter measurement[J]. Chinese Journal of Scientific Instrument，2003，24(4)：512-514.

[20] 张介秋，陈砚圃，梁昌洪，等. 交流电电气参量高精度测量的加权算法[J]. 仪器仪表学报，2005，26(2):172-176.

ZHANG Jieqiu，CHEN Yanpu，LIANG Changhong，et al. Weighted algorithm for high-accuracy measurement of AC electrical parameters[J]. Chinese Journal of Scientific Instrument，2005，26(2):172-176.

[21] 戴先中. 准同步采样及其在非正弦功率测量中的应用[J]. 仪器仪表学报，1984，5(4)：390-396.

DAI Xianzhong. Quasi-synchronous sampling and its application in non-sinusoidal power measurements[J]. Chinese Journal of Scientific Instrument，1984，5(4)：390-396.

[22] 戴先中. 准同步采样应用中的若干问题[J]. 电测与仪表，1988，5(2)：2-7.

DAI Xianzhong. A number of issues in quasi-synchronous sampling applications[J]. Electrical Measurement & Instrumentation，1988，5(2):2-7.