改进 Fuzzy-PID 控制在空调冷却水系统中的应用

龚嫒雯 赵龙章 吴扬 墨蒙

南京工业大学电气工程与控制科学学院

空调冷却水系统是一个滞后的、 时变的非线性系统， 不易建立精确的系统数学模型。 PID控制器结构简单、 稳定性能好、 调节精度高、 鲁棒性且易操作， 但超调量大、 快速性不理想且需要精确的数学模型。模糊控制适用于这种非线性的控制， 会存在延迟、 精度低等问题。Smith预估补偿只依赖于控制对象 [1] ， 对其他控制器不产生影响。因此， 本文将模糊控制与 PID 控制相结合， 并引入了Smith算法， 以改善系统的大滞后性问题。

1 冷却水控制系统分析

整个控制系统由传感器与变送器，调节对象， 调节器， 执行器， 比较器等组成。被调参数冷却水温度表示成t r； 设定值通常被表示成t g。实际值和设定值之间存在不一致应表示成e，e=tg-tr； 干扰表示成f。则如图1所示。

图1 冷却水系统控制图

中央空调系统的控制对象一般是高阶系统， 由于高阶模型计算困难、 较复杂， 因此， 本文采用低阶的方式近似控制对象， 二阶模型足以满足系统的精度要求。

二阶模型传递函数为：

2 Fuzzy-PID 控制分析

由于PID 控制器的线性特征， 使得控制性能在离工作点越近控制效果越好。而模糊控制虽然对控制的动态性能的改进和工作点的距离无关，鲁棒性强， 但稳态精度差， 在工作点附近振荡较大。因此， 本文在误差范围小时采用 PID 控制，在误差范围大时换成Fuzzy控制， 两者结合以达到更好的控制效果。

2.1 模糊控制原理介绍

模糊控制器在进行信号输入时， 要经过三步才可输出控制信号。1）将输入的模拟量转换成为电量， 由模数转换器将电量转换成数字量， 再转换成模糊集合的隶属函数。2） 根据专家的经验制定出规则， 通过模糊规则推理， 得出模糊输出集合。3） 根据模糊隶属函数， 计算出精确的输出值。

2.1.1 精确量的模糊化

控制器根据实际输出值和已设定的期望值之间的偏差值来决定如何对系统进行调整控制。通常把散的区间映射到输入量范围， 输入量的分辨率决定了区间数。隶属函数可以采用多种形状， 本文采用三角形的隶属函数。

据 Mamdani 的方法， 把[-6,+6]设定为偏差e(t)的变化范围。 如果输入量的范围不在[-6,+6]之间， 则假设其范围为[a,b]， 可以通过式 （2） 进行变换：

将其变换到[-6,+6]内， 在[-6,+6]之间进行分区间，每个区间则作为一个模糊子集，且对应一个隶属函数。一般分为如下5个区间：

“正大” （PB）： 可取+3～+6，

“正中” （PM）： 可取0～+6，

“零” （ZO）： 可取-3～+3，

“负中” （NM）： 可取-6～0，

“负大” （NB）： 可取-6～-3，

精确量的模糊化是将输入量转换为[-6,+6]之间的值， 由该值对前面已划分的隶属函数取得隶属度。

2.1.2 模糊规则的形成和推理

由专家的经验制定出模糊规则， 然后对原本用语言描述的模糊规则进行形式化处理， 模糊规则可以归纳表示成下面的形式：

A：if A then B

B：if A and B then C

C：if A then B else C

A：系统的设定值和受控对象的实际测量值之间的偏差e(t)；B ：偏 差的变化率de(t)/t。e(t)和de(t)/t按照精确量的模糊化方法，定 义不同的隶属函数，从 而得到模糊量。

2.1.3 模糊输出控制量的解模糊判决

模糊控制器经过模糊推理得到控制输出隶属函数，隶 属函数是不同取值的组合，表 示控制系统的模糊性。实际的工程中[2]， 要 控制一个受控系统，必 须保证随时都有一个明确的输出控制量，并 在输出的隶属函数中找到模糊控制的精确量，这 个过程就是模糊输出量的解模糊判决。

2.2 模糊PID控制系统的结构研究

模糊 PID 参数自整定控制系统是运用模糊推理的方式实现实现在线 PID 参数Kp，Ki和Kd的自整定，对控制过程中的参数改变、外 界干扰、不 确定的条件和延迟等因素进行检测和分析。既保留了常规PID控制的原理简单、鲁 棒性较强、使 用方便等特点，又 具有更大的适应性，灵 活性和精确性等特性[3]。

如图2 所示，模 糊控制部分对 PID 控制的控制参数Ki，Kp，Kd进行监督和自整定，此 系统的模糊控制器和PID 控制器协调工作，共 同控制系统。模糊控制器作为上层监督控制器，通 过监督系统的状态，对 底层控制器参数进行实时整定调整，PID 控制器作为底层控制环节，直接负责对象的控制。偏差和偏差变化率作为控制器模糊系统的输入，PID 参数值的变化作为输出，根 据已确定的模糊控制规则进行模糊推理在线改变 PID 参数值，以 实现 PID 的参数自整定，使 被控对象的动、静 态特性有良好的保障[4]。

图2 PID参数模糊自整定控制器结构

2.3 Fuzzy-PID控制器的设计

为提高系统的准确性和稳定性， 实现无差控制， 采用PID控制算法， 得到以下PID控制器输出控制量：

式中：Ti是积分时间；u(t)是 PID 控制器输出；TD是微分时间；Kd=Kp Td是微分系数；Kp是比例系数；Ki=Kp/Ti是积分系数。

模糊控制器用 2个输入 1个输出的控制方式，以温度偏差（e）和 误差变化率（ec） 作 为输入变量，以u作为输出变量。模 糊子集为E=EC=U={负大，负 中，负 小，零，正小，正中，正大}={NB，N M，N S，Z O，PS，PM，PB}。将3 个语言变量的量化等级分为 11 级，取{-5,-4,-3,-2,-1,0,1,2,3,4,5}，其 中偏差变化率（ec） 的 论域为[-100，100]，偏 差（e）的 论域为[-20,20]，控 制器输出u的论域为 [-18,18]。e，ec和u的量化因子分别为Ke，Kec，Ku，则Ku=3/20，Kec=3/100，Ku=18/3。

3 基于Smith预估控制算法的控制研究

系统的滞后环节使得系统相位出现滞后， 伴随滞后的时间增加， 相位滞后也增加， 并降低系统的稳定性， 使控制质量下降[5]。Smith 算法通过估计对象的动态特征， 用预估模型进行补偿， 使得反馈到控制器的被调节量没有时滞。为提高系统的稳定性，Smith预估器在调节器的两端并联反馈补偿网络。则结果如图 3所示：

图3 Smith预估器结构图

图3 中，τm为对象模型的纯滞后估计值；GC(s)为辅控制器的传递函数；Gm(S)是预估器；GCO(s)为主控制器的传递函数；GO(S)e-τs为控制对象的传递函数；是模型。如图3有：

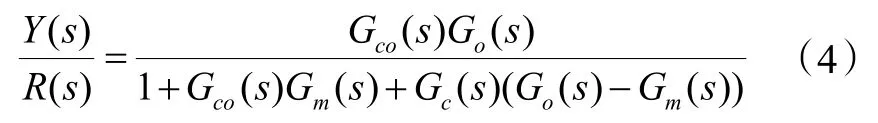
假设模型精确，Gm(S)=GO(S)， 则上式可简化为：

将上述反馈通道的传递函数视作一阶惯性环节，则调节器的积分时间常数与模型的时间常数相等[5]，则Gf(s)可以简化为:

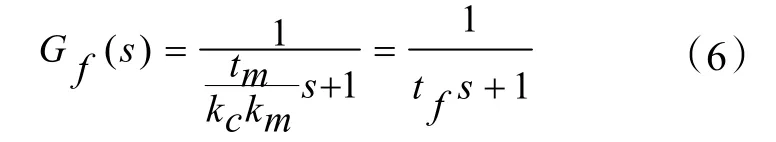
式中：kC为GC(s)的增益；tm为预估时间常数；t f=tm/kC km为滤波时间常数；km为Smith的预估器增益。

因此， 可简化为图4：

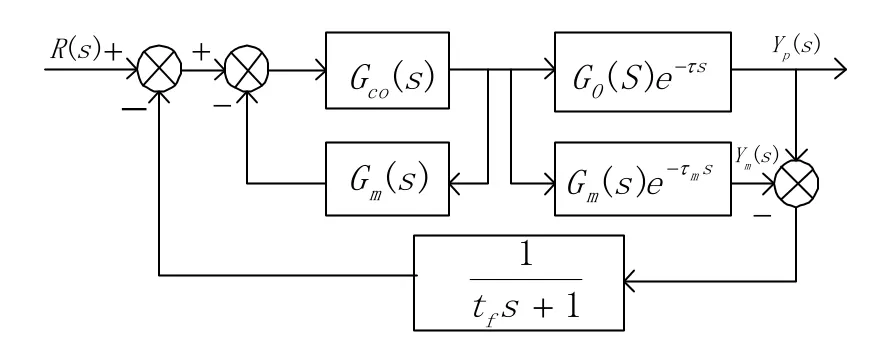
图4 Smith预估器简化图

由图4得到闭环系统的传递函数为：

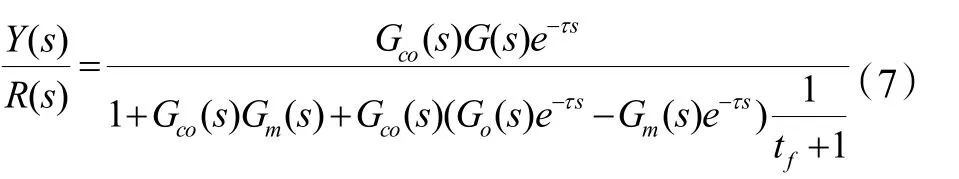
在全补偿的情况下， 有：

此时传递函数为：

用 Smith 预估补偿算法对空调系统进行控制,通过整定控制器GCO(s)， 使系统有很好的动态特性。1+GCO(s)Gm(s)=0为特征方程， 以消去原系统的特征方程中的滞后项e-τs，相当于将时滞因子移到了系统闭环之外，避免了滞后性对系统稳定性的影响。 因此,在对此控制器进行设计时,难度降低， 如同对无滞后环节的系统设计一样。

传递函数分母多了一个 1/(tf+1)因子， 当预估器出现误差时， 通过调整tf改善闭环系统特征方程的根， 从而提高控制系统的性能。

如图4所示，在主反馈通道中引入一个作用相当于低通滤波器的一阶惯性环节 1/(tf+1)， 预估器的输出Ym(s)和被控对象的输出Ys(s)之间的偏差经一阶惯性环节的滤波处理， 反馈到控制器， 使模型不匹配对系统的影响减弱， 同时模型误差对系统的干扰速度下降， 提高系统的稳定性。

4 仿真分析

根据已确定的冷却水控制系统的数学模型, 假设控制系统的被测温度初始值为 40 ℃，温度设定值为25 ℃，利用MATLAB的Simulink工具对控制系统的三种控制方式进行仿真分析， 仿真结果如图5所示。

由图5 可以看出， 传统的PID 仿真曲线有超调量大， 响应时间长和稳态误差大的缺点。而模糊控制只能在大范围内对系统进行控制，精度非常低。基于Smith自适应算法的Fuzzy-PID 控制响应时间快， 调整时间短， 振荡时间少， 控制精确， 超调量也得到较大的改善， 该控制方式使系统具有较强的自适应能力和鲁棒性， 使冷却水系统的控制得到很好的改善， 使系统温度趋于设定值25℃。

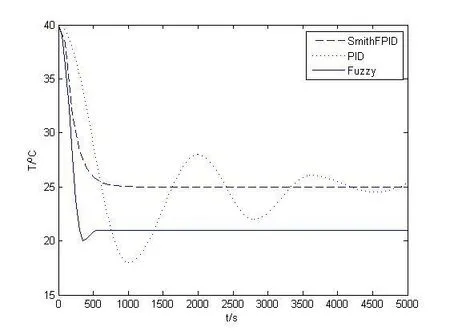
图5 三种控制响应曲线

5 总结

本文根据空调冷却水系统的时变性、非线性、 大时滞特点， 利用模糊控制具有不依赖被控对象精确模型的特点， 由模糊控制在线整定 PID 控制器参数。本文为改善空调冷却水系统的时滞性问题，引入了Smith预估控制算法，时滞性对系统动态性能的干扰降低。通过仿真分析发现算法存在的不足和问题并有针对性的提出改进，使 Smith 预估器对 Fuzzy-PID 控制进行改进，最终使系统达到理想的动态响应。文章最后将传统PID， 模糊控制及Smith-Fuzzy-PID 控制进行了仿真对比分析， 由仿真结果可知 Smith-Fuzzy-PID控制要优于另外两种， 为系统稳定高效的运行提供了保障。

参考文献

[1] 司轶芳,孙曼利,王楠.模糊自适应控制在中央空调系统中的节能研究[J].装备制造,2009,(8):140-192

[2] 王斌, 郭翠爱, 温曙光.钢球磨煤机的模糊控制[J].热力发电,2004,33(11):51-53

[3] 杨晓亚.微流量传感器及其在压电泵闭环控制中应用[D].哈尔滨: 哈尔滨工业大学,2009

[4] 华山.基于虚拟仪器技术的微反应器控制系统设计与实现[D].上海:上海交通大学,2009

[5] 崔颖. 基于 Smith预估器的模糊 PID控制方法研究[D].大连:大连理工大学,2015