南海东沙环礁附近第二模态内孤立波生成过程的数值模拟

陈同庆 ，张庆河

(1. 天津大学水利工程仿真与安全国家重点实验室，天津 300072；2. 大连理工大学海岸和近海工程国家重点实验室，大连 116024)

南海东北部海域是内孤立波出现较多的海域，内孤立波对该海域的生态环境、油气资源开发、水下潜航器安全等具有重要的影响[1-3]，其生成、传播、演变机制的研究受到广泛关注.该海域早期现场观测所发现的内孤立波多为第一模态，即水平流速在垂向上呈上层与下层相反的两层结构，很少发现第二模态(水平流速在垂向上呈三层结构，上层与下层相同，并与中间层相反)内孤立波[4-6].近年，在东沙环礁附近的陆坡陆架区域进行的现场观测多次发现第二模态内孤立波，如在亚洲海国际声学实验(ASIAEX)1999年先期实验和2001年正式实验期间，Yang等[4]和Duda等[7]分别从东沙环礁附近海域观测数据中各发现一个第二模态内孤立波.在 2005年 4月—7月和2005年11月—2006年2月的长期观测中，Yang等[5]在该海域陆架坡折处附近测点数据中发现了多个第二模态内孤立波.

目前，关于南海东北部东沙环礁附近陆坡陆架区域第二模态内孤立波生成过程的研究仍比较少.第二模态内孤立波是一种相对不稳定的结构，不能如第一模态内孤立波一样传播很长的距离，Yang等[4]在观测中所发现的第二模态内孤立波出现位置距离吕宋海峡较远，因此，Yang等[4]认为其由吕宋海峡处生成进而传播至东沙环礁附近海域的可能性较小，可能为陆坡陆架区域局地生成.Yang等[5]从 2005年夏季陆架坡折处附近测点数据中发现，第二模态内孤立波常出现于第一模态内孤立波经过该测点一定时间之后，而深水区测点所观测的内孤立波主要是第一模态内孤立波，并未发现第二模态内孤立波，因此，Yang等[5]认为陆坡陆架区域观测到的第二模态内孤立波可能与第一模态内孤立波的浅水变形过程有关.Liu等[8]对观测资料的理论分析也认为第二模态内孤立波源于第一模态内孤立波.Guo与 Chen[9]在理想地形的情况下，将第二模态内孤立波作为入射波，利用二维非静压模型模拟分析了陆坡陆架区域第二模态内孤立波的演变过程，但未讨论第二模态内孤立波的生成过程.Chen等[10]利用二维非静压模型在理想海脊地形条件下对层化条件对第一模态与第二模态内孤立波的影响进行了讨论.Qian等[11]利用二维非静压模型在简化后的地形上对内孤立波在陆坡陆架区域的演变进行了模拟，认为第二模态内孤立波源于第一模态内孤立波与底部地形的相互作用.

目前结合东沙环礁附近海域实际地形条件阐明第二模态内孤立波生成过程的文献鲜有报道.因此，本文根据南海的实际地形条件，建立内孤立波三维非静压数值模型，针对第二模态内孤立波的生成过程进行模拟，根据模拟结果分析其生成机制.

1 数学模型

1.1 控制方程

南海东北部海域内孤立波数值模型基于 Fringer等[12]的海洋模型 SUNTANS建立.该模型采用非静水压力假定，通过压力泊松方程求解压力.模型在Boussinesq近似条件下的主要控制方程为

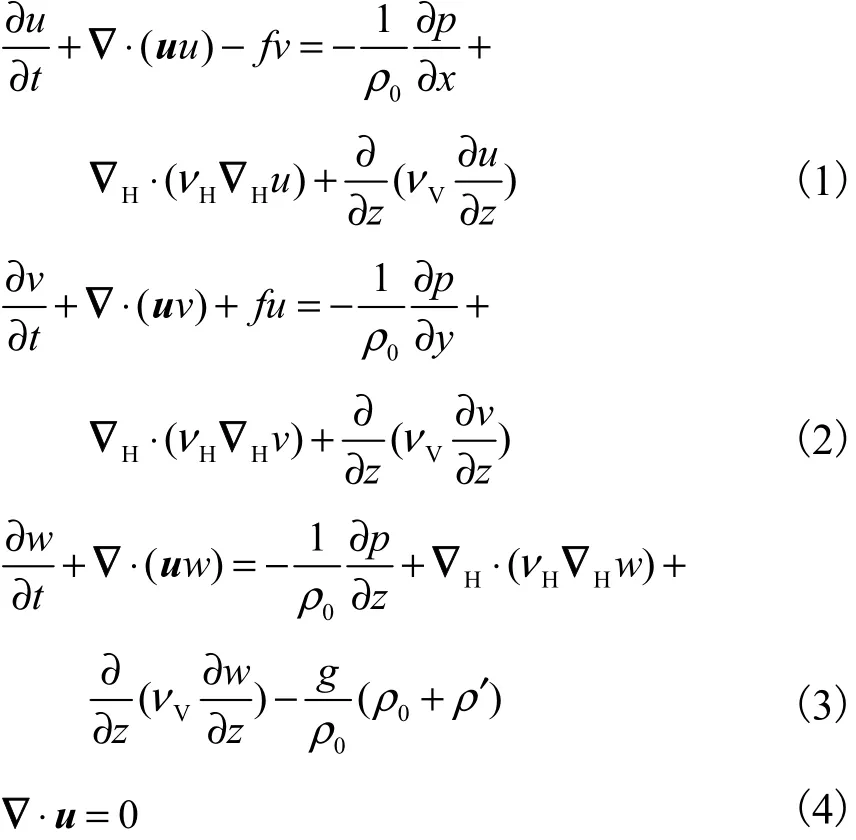
式中：u为速度矢量，其在 x、y、z方向的分量分别为u、v、w；t为时间变量；f为科氏力参量；ρ0为参考密度；ρ′为密度扰动量；νH和νV分别为水平向和垂向涡黏系数；p为总压力，p = ps+ ph+q，其中 ps为表面气压，ph为静水压力，q为非静水压力；水平梯度算子为

总密度ρ=ρ0+ρ′可由以下状态方程计算

水体的温度 T和盐度 s可由如下对流扩散方程进行求解

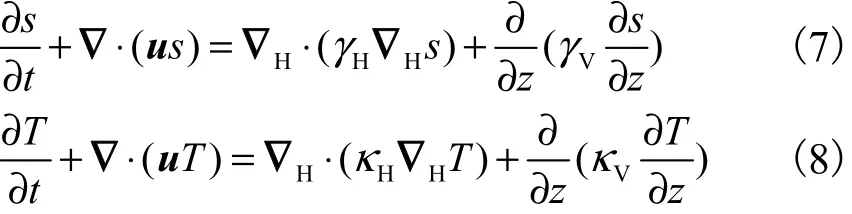
式中：Hγ和Hκ分别为水平向的质量扩散系数和热扩散系数；Vγ和Vκ分别为垂向的质量扩散系数和热扩散系数.

SUNTANS模型已经在南海东北部海域内孤立波生成与传播演变的模拟中得到应用[13-14].原始SUNTANS模型水平涡黏系数采用常数，陈同庆等[14]将 Smagorinsky模式引入 SUNTANS模型计算水平涡黏系数，本文计算中将采用该模式进行计算.

1.2 模型设置

模型计算范围如图1所示，模型所采用的水深数据取自Ⅰ空间精度的 ETOPO1数据[15]，岛屿边界根据中国人民解放军海军司令部航海保证部海图确定.开边界处以流速驱动，边界上的正压潮(表面潮)流速从OTIS潮流模型[16]China Seas 1/30°数据中提取. 水平方向网格采用三角形网格，网格尺寸约为500～4,000,m，岛屿边界处较细，而开边界处较粗.垂向分层进行求解，分为 100层，表层网格高约为10,m，向下逐渐增大.模型时间步长取为 15,s，计算时间为2005年6月17日0时—7月1日0时. 水平向和垂向涡黏系数分别采用 Smagorinsky模式和Mellor-Yamada 2.5阶湍流模型进行计算，背景的垂向涡黏系数取为 10-4,m2/s.初始流速为零，初始温度、盐度垂向分布根据 Zhang等[13]给出的实测数据进行设置.温盐控制方程的求解采用二阶 TVD格式.为消除开边界处内波反射对内场的影响，利用 Zhang等[13]的方法进行阻尼消波.

Zhang等[13]与陈同庆等[14]分别利用 SUNTANS模型建立了南海东部海域的内孤立波数值模型，利用实测资料对模拟结果进行了验证，说明了模拟结果的合理性，本文所用模型与主要参数与上述工作相同，限于篇幅，不再对模型验证进行赘述.

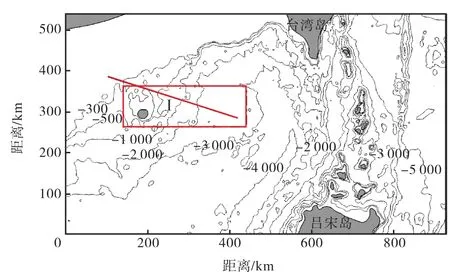
图1 模型计算范围及水深Fig.1 Computational domain and bathymetry

2 模拟结果与讨论

2.1 生成过程

在数值模拟中，内孤立波不是在边界上输入的，而是在模型中模拟了南海东北部海域内孤立波的生成，其主要源于吕宋海峡及其附近海域表面潮(正压潮)与底部地形的相互作用[13]，生成的内孤立波主要是第一模态，关于该海域第一模态内孤立波的生成过程，Zhang等[13]进行了详细的讨论，本文主要目的是分析讨论内孤立波传播至陆坡区域后第二模态内孤立波的生成，不再对第一模态内孤立波的生成过程进行详细讨论.

取图1中虚线框范围内的温度场，如图2所示，从图中可见内孤立波传播至陆坡区域与底部地形发生相互作用，图2范围内模拟结果在南北向出现一定的变化，有明显的三维性，与垂向二维模型结果有所不同.取图 1中所示代表剖面Ⅰ处的温度场计算结果(见图 3)，对东沙环礁附近海域第二模态内孤立波的生成过程进行分析.

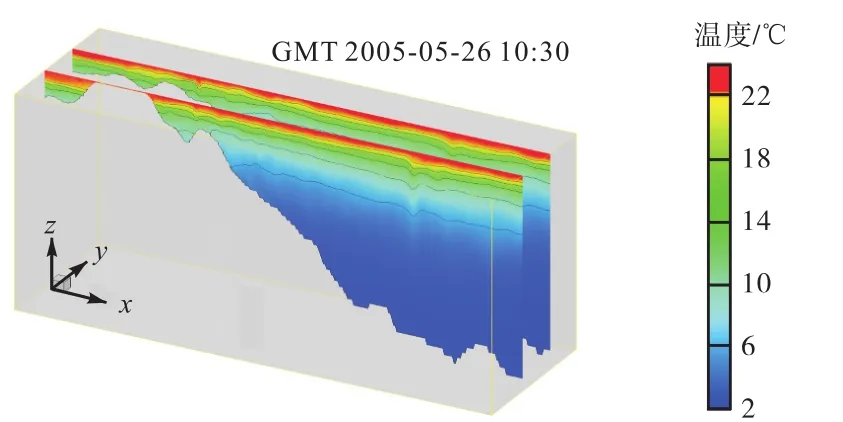
图2 陆坡附近内孤立波模拟结果Fig.2 Simulated results of internal solitary waves near the continental slope

如图 3(a)所示，从吕宋海峡附近海域生成的下陷型第一模态内孤立波a0传播至陆坡上部，波a0为波列中的第一个波，其后为波幅相对小一些的内孤立波 c0.关于南海东北部第一模态内孤立波的生成过程，详见 Zhang等[13]的讨论.各波继续向西传播，由于与底部地形的相互作用，在波 a0后裂变出波幅较小的波动，同时，如图 3(b)～(d)所示，波 a0所在波列中的波c0也发生了变形，波c0在上层水体中的波后坡在传播过程中逐渐变陡，而在下层水体中形成等温线向上凸的结构.

在上层水体中，波 c0后坡逐渐变陡的过程与第一模态内孤立波向陆架区域传播过程中的浅水变形(shoaling)有关，Shen等[17]对内孤立波的浅水变形进行了模拟分析，下陷型第一模态内孤立波传播至浅水区域，由于与底部地形的相互作用，波的后坡会逐渐变陡.

波c0在下层水体中的变化过程主要受陆坡上部内潮散射作用的影响.Klymak等[18]基于实测资料对内潮传播至南海东北部陆坡上部的散射进行了分析，其结果表明由于散射作用内潮在陆坡上部坡度变化处会形成斜向的内潮射线结构.将图 3(b)对应时刻流速计算结果减去垂向平均流速得到斜压流速.东西向斜压流速结果见图 4，图 4中虚线框为图 5范围，图 5为剖面Ⅰ斜压流速计算结果(流速垂向尺度进行了放大).由图 4中可见陆坡上部存在较明显的内潮射线.由于内潮射线的影响，陆坡上部靠近底部处形成如图5所示的斜向上的流动，受此斜向流动的作用，底部水体向上隆起，见图 3(b)，由此在下层水体中逐渐形成等温线向上凸的结构.至图 3(d)所示时刻，波 c0形成上层向下而下层向上的第二模态内波形式，Duda等[7]在其现场观测中也发现了图 3(d)中波 c0形式的第二模态内波，并将其称为内涌(bore).继续向西传播，如图 3(e)所示，波c0形成凸起型第二模态内孤立波，即上层向上凸起而下层向下凹，且c0其后形成另一第二模态内波.

图3 剖面Ⅰ处第二模态内孤立波生成过程模拟结果Fig.3 Simulated results of the generation process of the second mode internal solitary wave along the sectionⅠ

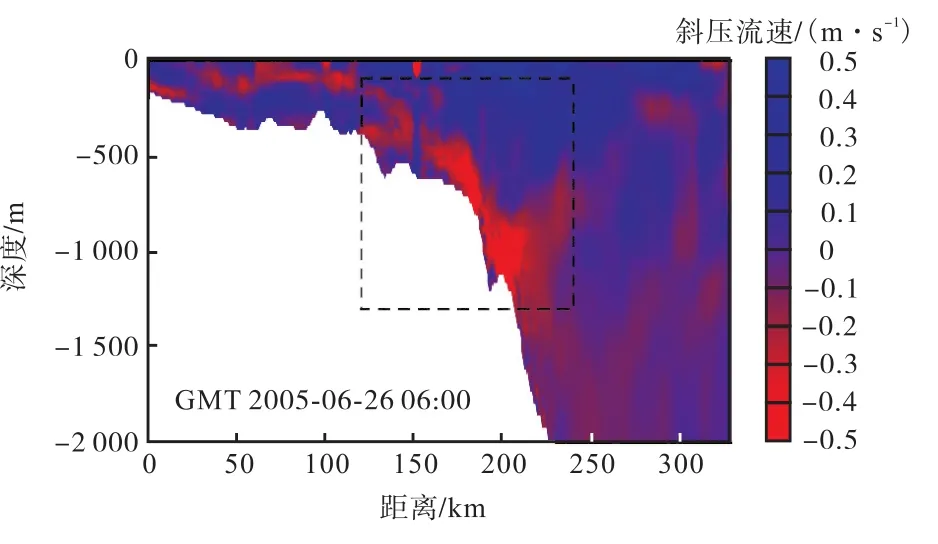
图4 剖面Ⅰ东西向斜压流速计算结果Fig.4 Simulated results of zonal baroclinic velocities along the sectionⅠ

综合以上分析可见，模拟结果在陆坡上部出现的第二模态内孤立波的生成机制主要包括2方面：①第一模态内孤立波与底部地形的相互作用；②内潮射线的影响.另外，模拟结果中第二模态内孤立波 c0出现在第一模态内孤立波 a0后面一定距离处，这与Yang等[5]从夏季观测资料中发现的规律是一致的.

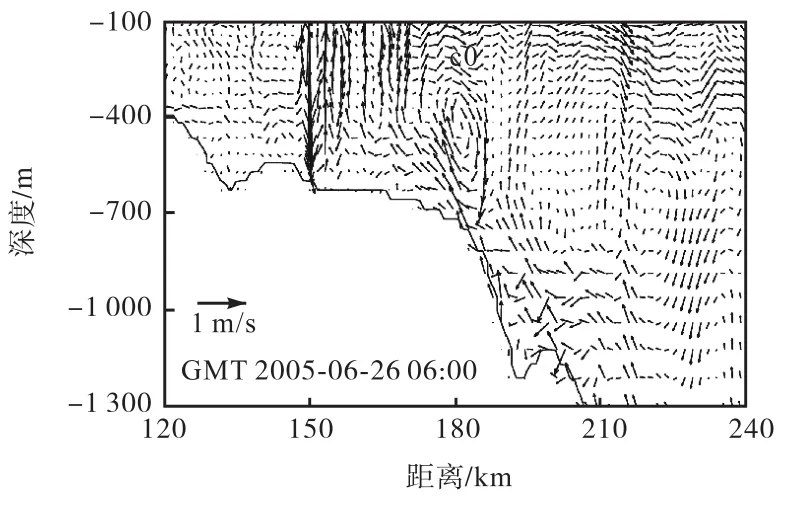
图5 剖面Ⅰ斜压流速计算结果(流速垂向尺度进行了放大)Fig.5 Simulated results of baroclinic velocities along the sectionⅠ(the vertical scale of velocities is amplified)

2.2 流速结构

图 6(a)～(c)分别给出了内孤立波 a0、b1、c0导致的水体斜压流速垂向结构，各子图时刻分别与图3(b)、3(e)、3(d)时刻相对应.图中所示内孤立波 a0与 b1流速具有第一模态内孤立波的两层流速结构，即上层水体与下层水体水平向流速相反[8]，而内孤立波 c0具有第二模态内孤立波的三层流速结构，即上层水体与下层水体水平向流速相同，并与中间层相反[8].从流速结构看，模拟结果中的内孤立波c0具备第二模态内孤立波的特征.

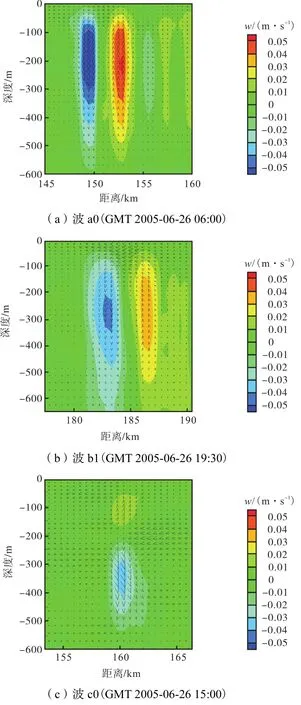
图6 内孤立波流速垂向结构(流速垂向尺度进行了放大)Fig.6 Vertical structure of velocities for solitary waves(the vertical scale of velocities is amplified)

2.3 传播速度

根据图 3(a)～(b)陆坡上部第一模态内孤立波a0在不同时刻的位置，计算得到第一模态内孤立波在此处的传播速度约为 1.97,m/s.根据图 3(c)～(e)陆坡上部内孤立波 c0在不同时刻的位置，计算得到内孤立波 c0在此处的传播速度约为 0.87,m/s，其值约为第一模态内孤立波波速的1/2.

理论上内波的波速可由本征方程式(9)求出[19]

式中：W为内波垂向特征函数；c为波速；N为浮性频率，N =[-(gdρ) /(ρdz)]，可根据模拟得到的水体密度垂向分布求出，见图7.利用数值方法对式(9)进行求解可得各模态对应的波速，第一模态波速为1.96,m/s，第二模态波速为 0.99,m/s，理论值与数值模拟结果吻合较好.从波速角度看，数值模拟结果是合理的，模拟结果中的内孤立波 c0具备第二模态内波波速的特征.

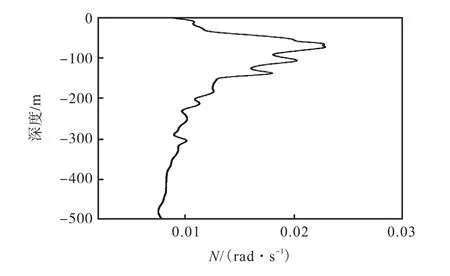
图7 浮性频率垂向分布Fig.7 Vertical distribution of buoyancy frequency

3 结 论

(1) 利用三维非静压海洋模型 SUNTANS，在南海实际地形条件下建立了南海东北部海域内孤立波数值模型，对东沙环礁附近海域第二模态内孤立波的生成过程进行了模拟与分析.

(2) 在东沙环礁附近的陆坡陆架区域，利用所建立的数值模型模拟出了第二模态内孤立波，其出现在第一模态内孤立波后面一定距离.与第一模态上、下层水体水平向流速相反的两层结构不同，第二模态内孤立波流速在垂向上呈三层结构，即上层水体与下层水体水平向流速相同，并与中间层相反.

(3) 根据内孤立波不同时刻的位置计算结果，第一模态与第二模态内孤立波的传播速度分别约为1.97,m/s和 0.87,m/s.第二模态内孤立波的传播速度计算结果约为第一模态的 1/2，波速计算结果与理论分析一致.

(4) 生成过程的分析表明，东沙环礁附近海域的第二模态内孤立波可能源于第一模态内孤立波和底部地形相互作用与内潮的联合影响.

：

［1］ 蔡树群，何建玲，谢皆烁. 近 10年来南海孤立内波的研究进展[J]. 地球科学进展，2011，26(7)：703-710.Cai Shuqun，He Jianling，Xie Jieshuo. Recent decadal progress of the study on internal solitons in the South China Sea[J].Advances in Earth Science，2011，26(7)：703-710(in Chinese).

［2］ 宋志军，勾 莹，滕 斌，等. 内孤立波作用下 Spar平台的运动响应[J]. 海洋学报，2010，32(2)：12-19.Song Zhijun，Gou Ying，Teng Bin，et al. The motion responses of a Spar platform under internal solitary wave[J].Acta Oceanologica Sinica，2010，32(2)：12-19(in Chinese).

［3］ 尤云祥，李 巍，时忠民，等. 海洋内孤立波中张力腿平台的水动力特性[J]. 上海交通大学学报，2010，44(1)：56-61.You Yunxiang，Li Wei，Shi Zhongmin，et al. Hydrodynamic characteristics of tension leg platforms in ocean internal solitary waves[J].Journal of Shanghai Jiaotong University，2010，44(1)：56-61(in Chinese).

［4］ Yang Y J，Tang T Y，Chang M H，et al. Solitons northeast of Tung-Sha Island during the ASIAEX pilot studies[J].IEEE Journal of Oceanic Engineering，2004，29(4)：1182-1199.

［5］ Yang Y J，Fang Y C，Chang M H，et al. Observations of second baroclinic mode internal solitary waves on the continental slope of the northern South China Sea[J].Journal of Geophysical Research，2009，114：C10003.

［6］ Ramp S R，Yang Y J，Bahr F L. Characterizing the nonlinear internal wave climate in the northeastern South China Sea[J].Nonlinear Processes in Geophysics，2010，17(5)：481-498.

［7］ Duda T F，Lynch J F，Irish J D，et al. Internal tide and nonlinear internal wave behavior at the continental slope in the northern South China Sea[J].IEEE Journal of Oceanic Engineering，2004，29(4)：1105-1130.

［8］ Liu A K，Su F C，Hsu M K，et al. Generation and evolution of mode-two internal waves in the South China Sea[J].Continental Shelf Research，2013，59：18-27.

［9］ Guo C，Chen X. Numerical investigation of large amplitude second mode internal solitary waves over a slopeshelf topography[J].Ocean Modelling，2012，42：80-91.

［10］ Chen Z，Xie J，Wang D，et al. Density stratification influences on generation of different modes internal solitary waves[J].Journal of Geophysical Research，2014，119(10)：7029-7046.

［11］ Qian H B，Huang X D，Tian J W，et al. Shoaling of the internal solitary waves over the continental shelf of the northern South China Sea[J].Acta Oceanologica Sinica，2015，34(9)：35-42.

［12］ Fringer O B，Gerritsen M，Street R L. An unstructuredgrid，finite-volume，nonhydrostatic，parallel coastal ocean simulator[J].Ocean Modelling，2006，14(3/4)：139-173.

［13］ Zhang Z， Fringer O B， Ramp S R. Threedimensional，nonhydrostatic numerical simulation of nonlinear internal wave generation and propagation in the South China Sea[J].Journal of Geophysical Research，2011，116：C05022.

［14］ 陈同庆，张庆河. 不同 TVD 格式对内孤立波数值模拟结果影响研究[J]. 海洋科学，2013，37(6)：102-107.Chen Tongqing，Zhang Qinghe. Effects of TVD schemes on the numerical simulation of the internal solitary wave[J].Marine Sciences，2013，37(6)：102-107(in Chinese).

［15］ Amante C，Eakins B W. ETOPO1 1 Arc-Minute Global Relief Model：Procedures，Data Sources and Analysis[R]. National Geophysical Data Center，NOAA，USA，2008.

［16］ Egbert G D，Erofeeva S Y. Efficient inverse modeling of barotropic ocean tides[J].Journal of Atmospheric and Oceanic Technology，2002，19(2)：183-204.

［17］ Shen C Y，Evans T E，Oba R M，et al. Threedimensional hindcast simulation of internal soliton propagation in the Asian Seas international acoustics experiment area[J].Journal of Geophysical Research，2009，114：C01014.

［18］ Klymak J M，Alford M H，Pinkel R，et al. The breaking and scattering of the internal tide on a continental slope[J].Journal of Physical Oceanography，2011，41(5)：926-945.

［19］ Cai S，Long X，Gan Z. A method to estimate the forces exerted by internal solitons on cylindrical piles[J].Ocean Engineering，2003，30(5)：673-689.