螺旋槽干气密封运行特性的预测模型及试验研究

刘正先，田广胜，刘艳梅

(1. 天津大学机械工程学院，天津 300350；2. 天津大学化工学院，天津 300350；3. 尼特流体动力科技(天津)有限公司，天津 300382)

干气密封，即干运转气体润滑非接触式机械密封，是一种较为先进的旋转轴动密封形式[1-2]，具有泄漏量小、端面磨损小、能耗低和被密封介质不受污染等优势，正逐渐取代传统机械密封，广泛应用在石油、化工和冶金等领域[3-5].螺旋槽干气密封是目前应用最为广泛且技术较成熟的密封.端面开启力、泄漏量和气膜刚度等运行特性参数被证明是干气密封设计和运行时的关键性能参数[6-7].因此，通过对密封间隙流场分析进行密封性能预测具有重要的理论和实际意义.

目前螺旋槽密封运转特性的研究方法主要有 2个：一是以 Whipple[8]和 Muijderman[9]的“无限槽窄槽理论”为基础进行的理论简解法[10-12]，该方法通过对模型和方程做一定简化达到求解目的；另一个是基于 CFD方法实施的流场数值模拟求解方法，具有可计算条件广、准确度较高等特点，目前已逐渐成为干气密封性能分析中被广为接受的研究方法[13]，如采用有限元分析法对密封间隙流动规律和压力分布进行研究[14-16].刘正先等[17]、徐洁等[18]和冯向忠等[19]对密封间隙流场进行 CFD数值模拟，并对密封性能参数进行数值分析.丁雪兴等[20-21]引入滑移边界条件，对广义雷诺方程进行修正，计算微尺度效应下密封的运行特性.彭旭东等[22-23]基于气体润滑理论，建立了等温可压缩流二维雷诺方程，采用数值分析方法研究结构参数对运行特性的影响.上述数值方法可以获得准确的运行特性参数，但干气密封在多种工况下运行时，气膜厚度是在不断变化的，预测运转特性参数需要频繁调用数值求解器，计算量大且耗时.

为快速准确获得螺旋槽干气密封运转时的特性参数，本文基于 CFD数值模拟结果，采用函数拟合和二次耦合给出了螺旋槽干气密封端面开启力和泄漏量的预测模型，分别采用该预测模型和“窄槽理论”求解了试验各工况下的泄漏量、开启力等特性参数，并将两种结果与试验测量值进行了对比分析，验证预测模型的有效性和可靠性.

1 计算模型与方法

根据螺旋槽密封原理，密封端面的气膜厚度为微米量级，依据可压缩性流体在小间隙中流动的特点，在进行理论分析时做如下物理假设：工作介质符合牛顿黏性定律；沿气膜厚度方向气体压力和密度不变；气体黏度不变；忽略系统扰动对气膜流场的影响[24].

本文采用层流模型计算，控制方程为可压缩稳态下气膜动态参数方程，其极坐标形式[24]为

式中：p为压力，Pa；h为气膜厚度，m；r为半径，m；μ为气体动力黏度，Pa⋅ s；ρ为密度，3kg/m ；ω 为角速度，rad/s.

式(1)为非线性偏微分方程，难以解析求解，采用CFD数值模拟方法求解.

2 基于CFD的数值拟合求解方法

2.1 几何结构参数

图 1为螺旋槽干气密封端面示意.其中：ro为密封端面外半径；ri为端面内半径；rg为螺旋槽槽根半径；α为螺旋角，定义为过螺旋槽型线上任意一点所做的切线与该点处线速度(ωr)的夹角；螺旋线方程为，θ为极坐标角度，rad.

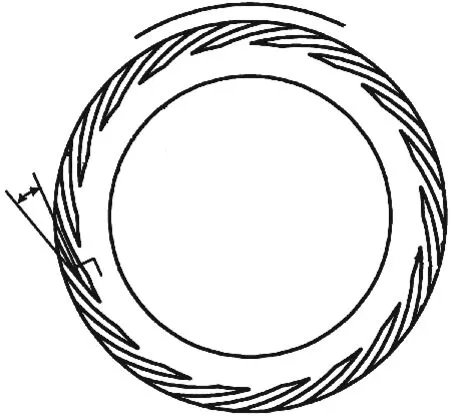
图1 螺旋槽几何模型Fig.1 Geometrical model of spiral grooves

以某螺旋槽干气密封产品为研究对象，结构参数如表1所示，运行参数包括入口压力po、出口压力pi及转速ω.

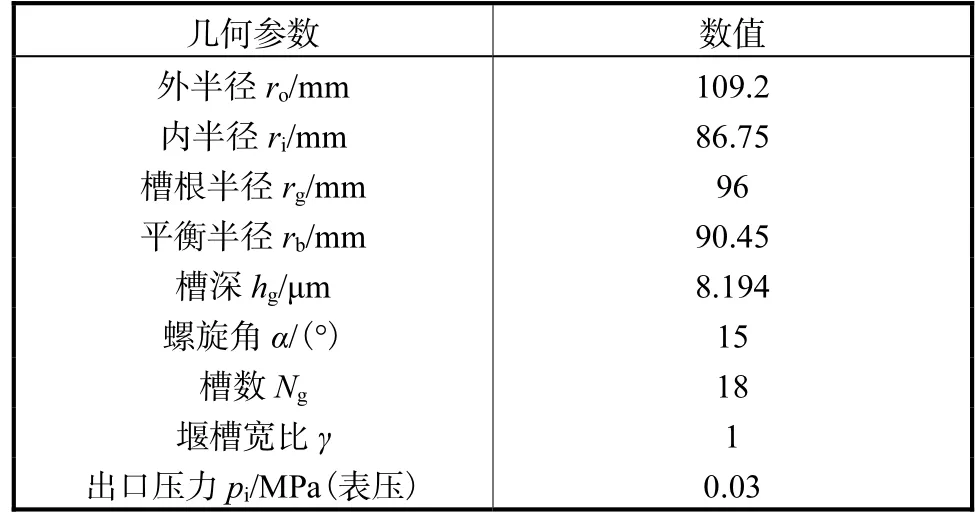
表1 结构及运行参数Tab.1 Geometry and operating parameters

2.2 CFD数值模拟

选取单通道螺旋槽结构作为计算模型，为便于观察，将计算区域厚度方向放大 1,000倍，如图 2所示.采用SIMPLE算法实施可压缩离散方程的计算，直至收敛(收敛标准 10-6).求解离散方程时，方程的扩散项采用中心差分格式，对流项采用 2阶迎风格式.旋转的动环流场采用旋转坐标系，转速为干气密封运行转速；计算域的进、出口分别设置为压力进口和压力出口条件；周期性边界条件如图 2所示，介质选择空气.

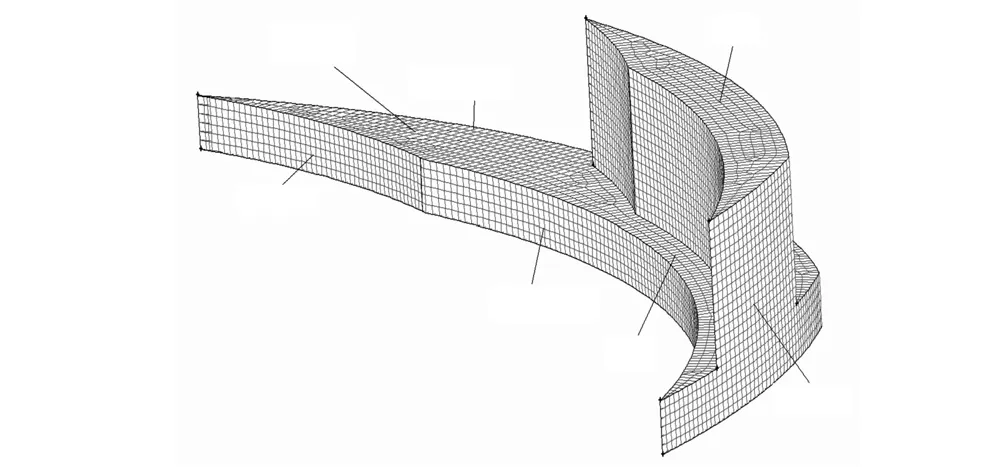
图2 计算模型及网格Fig.2 Computational model and mesh

由于相对流动方向的大尺度，气膜厚度方向尺度在 2～6,µm 之间，两者比值相差在 4,000倍以上，考虑到理论和数值模拟都确定流动参数在气膜厚度方向不变化，厚度方向网格只是为了计算泄漏量需要，因此虽然网格比值很大，但不会影响流场的计算精度.所以，网格生成时，长宽方向网格步长定为约0.1,mm，气膜厚度方向网格步长定为 0.5,µm，采用Cooper方法，生成六面体网格.流场网格如图 2所示，网格总数随气膜厚度不同，为(148～245)×104.

在 CFD求解获得气膜端面压力分布后，对整个端面数值积分得到开启力值；数值计算结果验证了压力在膜厚方向压力分布不变，数值的变化可以忽略；在沿径向方向，由入口到槽根处压力逐渐增大，并在槽根处达到最大值；由槽根处到出口处，端面的压力逐渐减小.

螺旋槽内气体速度是由于端面旋转引起的，因此在旋转面坐标系上，会产生周向和径向分速度，其变化根据能量伯努利方程与压力变化紧密相关.在气膜厚度方向，因既无压力差也无外力驱动，故可认为无速度分量.所以，泄漏量取出口截面的质量流量，并转换为“标准立方米/小时(Nm3/h)”单位.

2.3 数值拟合方法

研究过程中发现，在螺旋槽结构参数给定条件下，工作气膜厚度下的气膜开启力和泄漏量与入口压力和转速之间存在着耦合关系；运行工况一定时，气膜开启力和泄漏量又可以表示为气膜厚度的某种函数关系.

根据第 2.2节变参数下的数值计算结果，分别以压力、转速和气膜厚度为自变量，对开启力和泄漏量进行单变量多项式拟合，给定单变量拟合函数形式如下.

工作气膜厚度下，有

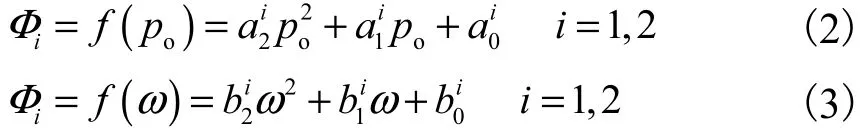
固定运行工况下，有

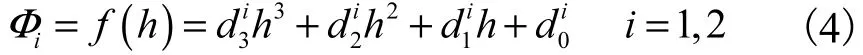
式中：i＝1 时，Φi为开启力；i＝2 时，Φi为泄漏量；ai与bi为拟合系数.

以上为单变量的拟合结果，笔者进一步发现，不同单变量关系式之间也可能存在耦合关系，因此采用函数二次耦合方法确定了以入口压力、转速和气膜厚度为自变量的运转特性参数的具有统一表达式的预测模型，利用该模型可以预测变入口压力或变转速条件下的气动特性参数.实施过程如下所述.

(1)根据单变量拟合函数，给定运转特性参数的多变量初始拟合函数形式为

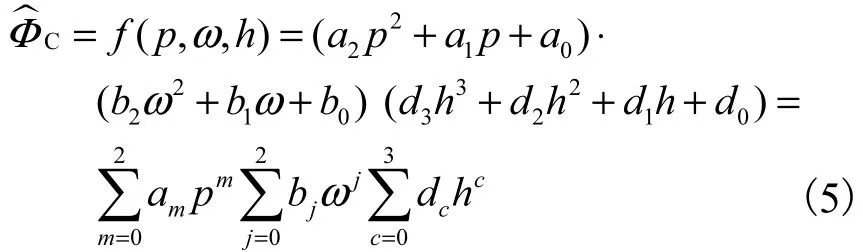
将式(5)因式项相乘展开，令；其中4j+c.对各展开项进行替换，式(5)可以写成多元线性回归方程

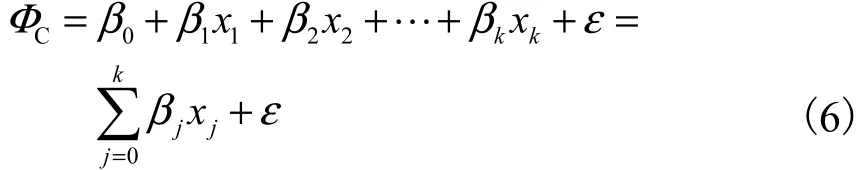
式中ε为计算偏差.

采用最小二乘法估算式(6)中的各系数值，方法如下.

假定运行特性参数Φ(开启力和泄漏量)与k个因子 x1, x2,…,xk相关，在变量计算空间内，经 DOE试验设计生成 n个计算样本，利用 CFD计算样本的运行特性参数，可得到表2中数据.表示模型中自变量的个数)，可将表 2中因子值和计算数据写成拟合函数形式，即

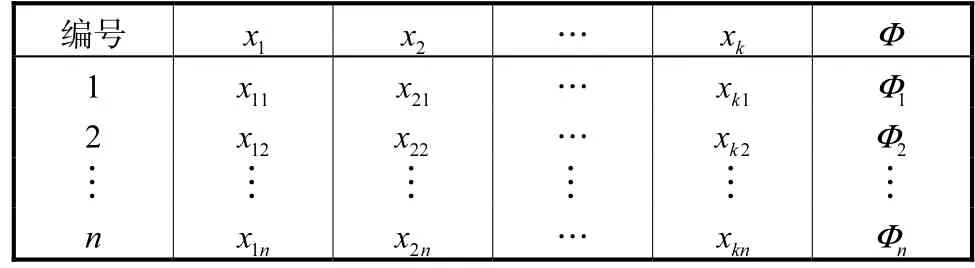
表2 多元线性回归的数据Tab.2 Data for multiple linear regression

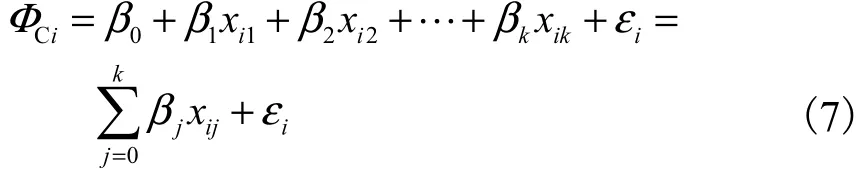
当满足矩阵形式为

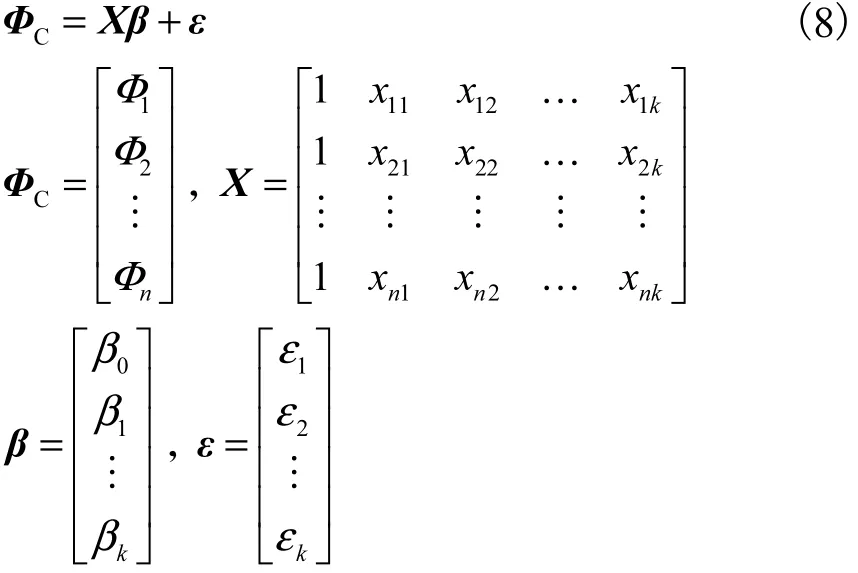
当式(8)的偏差平方和Tε ε达到最小，可得到

式中 b为 β的最小二乘估计，即为式(8)的最小二乘法解.

上述系数确定以后，初始预测模型可表示为

采用式(11)和式(12)的拟合优度指标来评价模型的拟合精度，其中相对均方根误差 RMSE代表模型的精度；确定系数2R度量模型预测值与真值之间差异程度，在 0～1取值，其值越接近1，说明误差的影响越小，模型拟合精度越高，可信度越高；对于多元回归选用修正后确定系数，剔除变量个数对拟合优度的影响[25].

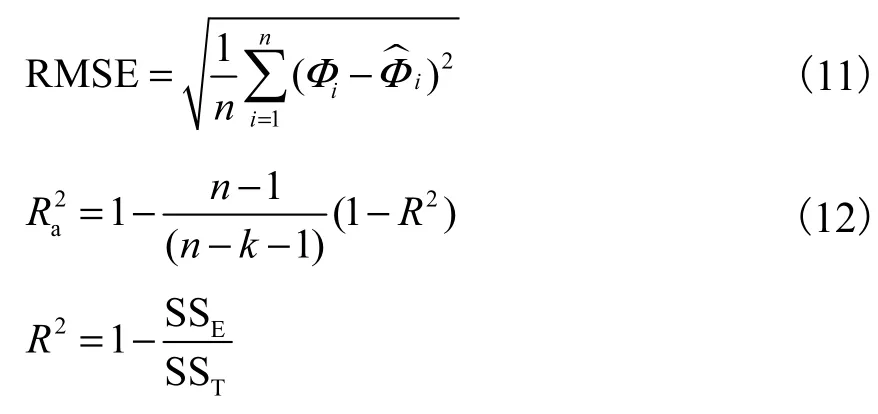
式中：表示模型预测值；SS= ΦTΦ-bTXTΦ ，表示

E和方差，即拟合数据和原始数据对应点的误差平方和；，表示总平方和，即原始数据和均值之差的平方和.

(2)对初始预测模型进行关键项取舍.选择各因式项(bjxij)对模型的平均贡献率N作为取舍标准，选取对模型贡献率高的关键项，舍去贡献率低的干扰项.

j N 计算方法为

j

式中，表示第i行各因式项贡献率.

将计算的值从大到小排序，选取贡献率高的16个因式项，构造二次拟合函数；采用步骤(1)中最小二乘法确定的各系数值.

(3)在函数二次拟合计算的基础上，利用式(13)计算各因式项的贡献率，并将其值从大到小排序，选择贡献率高的8个因式项，并在剩下8个因式中随机选取2个因式，构造三次拟合函数︿FΦ；计算每一种组合下函数的拟合优度指标并比较，选取相对均方根误差 RMSE最小的函数，作为最终确定的运转特性参数的预测模型.

(4)上述确定的预测模型，验证其拟合确定系数＞ 0.96，则模型具有可信度，可采用预测模型替代数值模拟计算；如不满足，则需要增加更多的样本数据.

计算流程如图3所示.，若满足

图3 数值拟合计算流程Fig.3 Fitting process based on CFD calculation

2.4 数值拟合结果分析

表 3为运行工况和气膜厚度参数的计算空间.选择入口压力、转速和气膜厚度作为输入变量，采用DOE试验设计中的拉丁超立方样本[26]选取方法建立36个样本点，保证了样本点在计算空间的均匀分布以及预测模型在整个计算空间的近似精度[27-28].

表3 变量计算空间Tab.3 Variables calculation space

选取运转特性参数(端面开启力和泄漏量)作为输出变量，采用 CFD数值计算，获取样本点的运转特性参数.采用第2.3节中数值拟合方法对上述数值结果实施拟合，确定运行特性参数的预测模型为

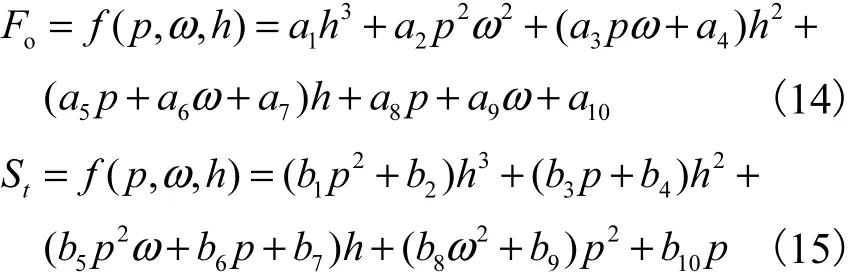
确定式(14)和(15)中的各系数值，如表4所示.

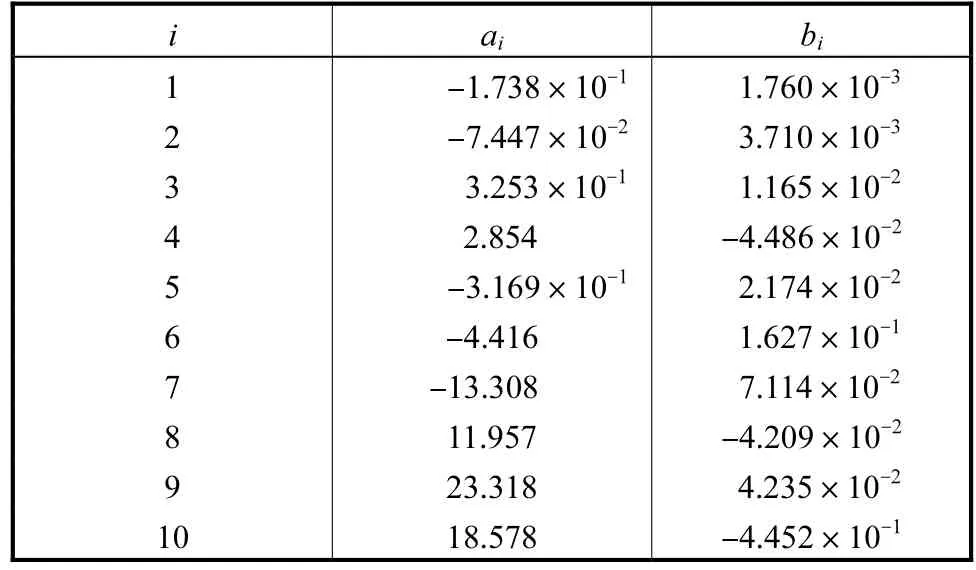
表4 拟合系数值Tab.4 Fitting coefficient values

计算式(14)和(15)的拟合优度参数的 RMSE和值，如表5所示.

由表 5可以看出接近于 1，RESM＜0.01，表明模型对于计算数据有较高的拟合精度和可信度.

每单位气膜厚度变化引起的开启力的变化称为刚度，可由式(14)导出气膜刚度(kN/μm)函数式，即

气膜刚度越大，表明密封稳定性就越高，越能抵制压力及其他机械扰动的变化.

3 数值预测与试验的对比

3.1 试验装置

为了验证预测模型的可靠性，在某公司的整机试验台上(图 4所示)对表 1中密封进行了相关试验测试.试验装置如图 5所示.该试验装置包括气源、试验台架、测控系统三部分.气源部分包括一台25,MPa的高压气泵、缓冲罐、过滤器、调压阀和管路.试验台主体由 20,000,r/min的高速变频电机、联轴器、轴承箱、主轴和试验腔体组成.

图4 干气密封试验台Fig.4 Test-bed of dry gas seal

图5 干气密封试验装置示意Fig.5 Schematic diagram of dry gas seal test device

根据试验台主轴尺寸和表 1密封件尺寸做了过渡轴套、试验腔体和试验端盖.在腔体表面用水进行冷却，模拟密封实际运转过程的受热情况.图 6为装配后干气密封的试验装置，安装于图 5中的红虚线区域.

各级密封的泄漏量采用 KRONE(克罗尼)H250/RR1/M9/ESK/EX/AIR型金属转子流量器测量，读数为换算到标况状态下的瞬时体积流量(Nm3/h)，精度为0.1,Nm3/h.考虑到实际运转中，2级密封进出口压差( Δp = 0.03MPa)很小，运转过程产生的泄漏量很小，约为 0～0.1,Nm3/h，用现有的流量器测不准，所以试验过程中将2级密封泄漏口堵住，因此试验测得的泄漏量可视为 1级密封泄漏.密封腔内气体温度的测量采用 WZP-236热电阻传感器，通过将热电阻传感器插入腔体内，使其与腔体气体接触，测出腔内气体的温度.

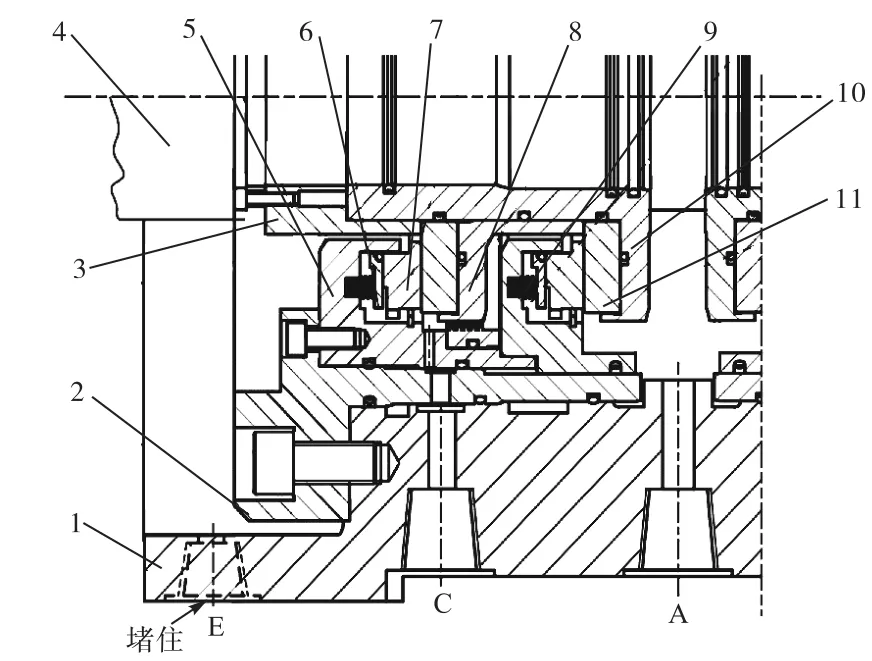
图6 试验装配示意Fig.6 Schematic diagram of test assembly drawing

3.2 试验内容

试验介质采用经过滤的空气，进气温度为室温；试验最大工作转速为 9,080,r/min，最大试验压力为5.20,MPa(表压)，1级密封的 pi＝0.03,MPa(表压)，静环所受的弹簧压力为 psp= 0.980 7 MPa .

考虑到工作人员巡视时现场检查参数，设计了节点显示模块，通过显示接口连接到节点。当工作人员现场巡视时需要某节点参数时，将显示模块连接到节点显示接口即可，这样可以避免每个节点都有显示模块导致成本增加，而且可以减少节点电能消耗。

在最大试验压力下稳定 0.5,h后进行动态测量，设置压力递增试验，压力由 1.0、2.5、4.0、5.0,MPa(表压)逐渐增大.初始压力设为 1.0,MPa，保持压力不变，初始转速设定为 4,000,r/min，试验每隔 5,min将转速增加 1,000,r/min，直至增到 9,000,r/min，然后降转速到 4,000,r/min，再将压力增加到下一值，依此循环直到压力为 5.0,MPa、转速 9,000,r/min，试验结束.每次改变工况后，待密封运转 1,min后，开始每隔 1,min记录一次试验数据，包括入口压力、转速、泄漏量和腔内气体温度等数据，最后取4次记录值的平均值作为最终试验数据.

3.3 试验各工况下泄漏量求解

3.3.1 泄漏量求解方法

对干气密封运转状态下的密封进行受力分析，如图 7所示.其中：Fc为端面闭合力，该力由静环后面密封介质压力po、pi引起的压力和弹簧压力psp组成；Fo为端面开启力，该力由作用在密封端面上受压缩的流体产生.图中虚线表示了不旋转时端面受到的气体力，实线表示旋转时密封端面受到的开启力.

在干气密封正常运转时，密封端面闭合力 Fc与开启力 Fo达到平衡，使动环与静环间维持一定间隙厚度稳定运转，此时通过气膜间隙的气体泄漏量等即为该工况下泄漏量；试验状态下测量的泄漏量也是密封受力平衡稳定运转下的泄漏量.

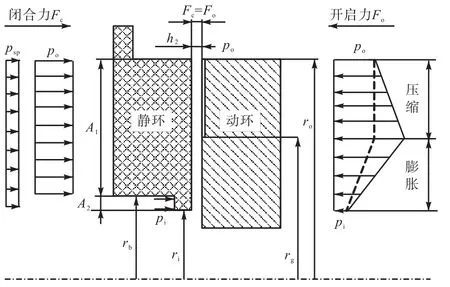
图7 干气密封运转时受力分析Fig.7 Force analysis of dry gas seal in operation

图 7中密封端面的闭合力 Fc和开启力 Fo分别为

式中：为平衡直径；p( r)为干气密封间隙沿半径的压力分布.当入口压力po、出口压力pi和支撑端面的弹簧压力都已知，闭合力Fc就可以由式(17)确定.

本文采用“窄槽理论”[9]和第2.4节预测模型计算出端面开启力；然后根据开启力与闭合力平衡的条件，确定出某工况运转下干气密封的端面气膜厚度，进而求出该工况下的泄漏量等特性参数.

基于 Whiple[8]和 Muijderman[9]的“无限槽数窄槽理论”基础上的平行槽模型端面压力分布结果，建立在某半径 r微环上的可压缩流体气膜的压力控制方程.

对于密封坝区(ri≤r ≤rg)，有压力分布

对于螺旋槽区(rg＜ r≤ro)，有

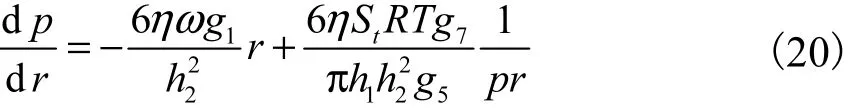
式中：h2为非槽区气膜厚度；h1为槽区气膜厚度，h1= h2+hg；hg为槽深；η为黏性系数；St为气体通过密封端面的质量流量，即泄漏量；T为气体温度；g1、g5、g7为螺旋槽系数.

采用龙格-库塔法[25]求解密封端面的气膜压力分布值，文献[12]已对给定工作气膜厚度条件下特性参数求解，而试验工况下密封运转过程是等闭合力条件，所以本文在原有基础上加入开启力与闭合力是否相等的判断；若相等，输出泄漏量等运转参数，否则重新迭代，直至满足条件.

3.4 试验验证

分别采用第 3.3节中螺旋槽窄槽理论简解法和第 2.4节中确定的预测模型关系式(14)、(15)计算与试验相同运行工况的泄漏量，做出两种方法计算的泄漏量与试验测量值随转速变化曲线，如图8所示.

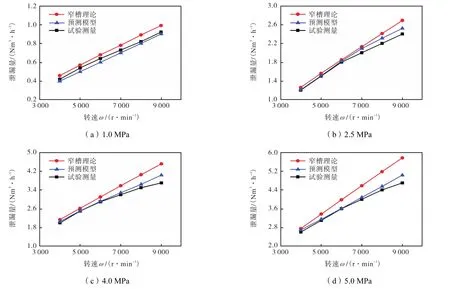
图8 试验与数值结果对比Fig.8 Comparison of experimental and numerical results

窄槽理论计算值St,th、预测模型预测值St,pr与试验测量值St,exp的相对误差分别为δth、δpr，其计算方法为

得到其相对误差如表6所示.

可以看出，两种方法的计算结果与试验结果保持了良好的分布趋势，泄漏量均随着转速的升高而增大.由表 6可以看出，“窄槽理论”的计算值在低压和高转速工况下相对误差较大，最大达到 22.7%,.而在各试验工况下预测模型计算值均小于“窄槽理论”计算值，与试验测量值符合更好，相对误差最大只有8.92%,，计算准确性明显提高.

分析泄漏量随转速变化的曲线可以看出，数值求解的泄漏量都略大于试验值；由数值计算得到的泄漏量随转速的升高基本呈线性增加，但是试验所得的泄漏量随转速增加而升高却较为缓慢，两者偏差也相应变大.产生误差的原因分析为：在 CFD计算中首先考虑了由气体的可压缩性对螺旋槽气动性能产生的温度影响，但忽略了温度升高对动、静环材料的热效应，即当气体温度较高时引起的动、静环的变形，可能会影响气膜开启力和泄漏量；由此当温度升高幅值较大时会造成计算和试验间的误差增大.由图 9试验测量的一级密封腔体气体温度可以看出，实际运转过程中，气体受到黏性力作用必然伴随着温度升高.黏度会随温度升高而增大，从而使气体的泄漏量变小，高转速下尤为明显.在后期工作中将进一步对此进行修正.

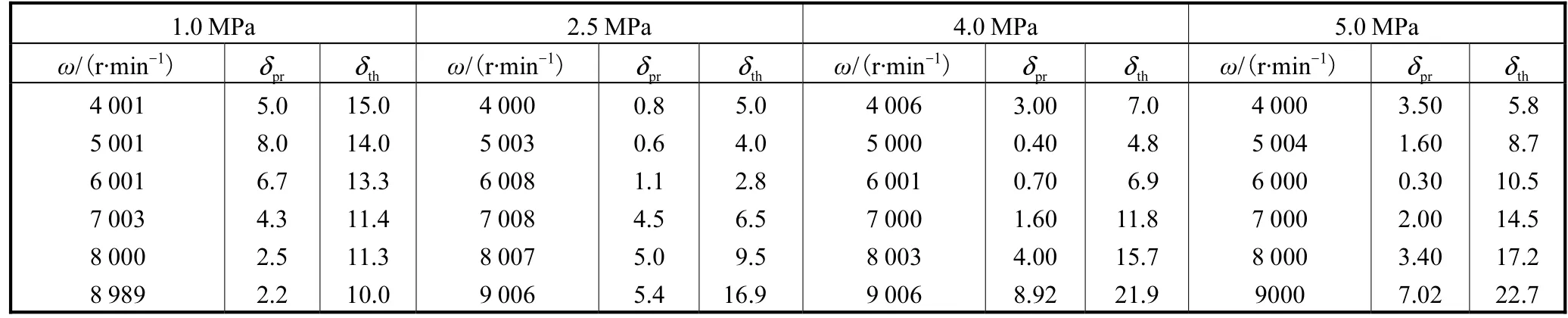
表6 计算值相对误差Tab.6 Relative error of calculation

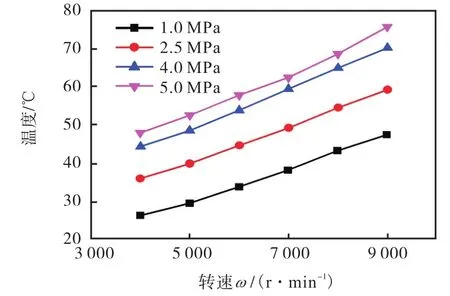
图9 试验测量的1级密封腔内气体温度Fig.9 Experimental results of gas temperature in the primary seal chamber

4 结 语

根据通用的干气密封螺旋槽几何参数，基于数值结果，通过单变量拟合和拟合函数的二次耦合，建立了以入口压力、转速和气膜厚度为自变量的端面特性参数(开启力、泄漏量和气膜刚度)预测模型.

分别采用“窄槽理论”和预测模型求解了与试验相同运行工况的泄漏量、开启力等运转特性，并将理论和数值两种结果与试验测量值进行了对比分析，可以看出：预测模型求解值与试验测量值符合更好，计算准确性明显提高.验证了本文基于数值结果的函数拟合与耦合方法的有效性.

本文预测模型可为干气密封螺旋槽的结构设计提供快速准确的气动和运行特性参数计算工具，避免了多次 CFD重复计算需要的大工作量，提高了设计效率.另外.预测模型为进一步明确气膜内在的动态规律和运行特性参数间的关联性提供了便利工具.

：

［1］ Fischbach M. Dry seal applications in centrifugal compressors[J].Hydrocarbon Processing，1989，68(10)：47-51.

［2］ 柳季君. 干气密封的工作原理及其典型结构[J]. 化学工业及工程技术，2002，23(4)：38-39.Liu Jijun. Working mechanism and typical structure of dry gas seal[J].Journal of Chemical Industry & Engineering，2002，23(4)：38-39(in Chinese).

［3］ 杨惠霞，王玉明. 泵用干气密封技术及应用研究[J].流体机械，2005，33(2)：1-4.Yang Huixia，Wang Yuming. Technology and industrial application of dry gas seals for centrifugal pump[J].Fluid Machinery，2005，33(2)：1-4(in Chinese).

［4］ Tournerie B，Danos J C，Frêne J. Three-dimensional modeling of THD lubrication in face seals[J].Journal of Tribology，2001，123(1)：196-204.

［5］ Saxena M N. Dry gas seals and support systems：Benefits and options[J].Hydrocarbon Processing，2003，82(11)：37-41.

［6］ 彭 建，左孝桐，顾永泉. 螺旋槽干气密封的优化设计[J]. 流体机械，1995，23(3)：24-27.Peng Jian，Zuo Xiaotong，Gu Yongquan. Optimum design of spiral groove dry gas seal[J].Fluid Machinery，1995，23(3)：24-27(in Chinese).

［7］ 蒋小文，顾伯勤. 螺旋槽干气密封端面间气膜特性[J]. 化工学报，2005，56(8)：1419-1425.Jiang Xiaowen，Gu Boqin. Characteristic of gas film between spiral groove dry gas seal faces[J].Journal of Chemical Industry and Engineering，2005，56(8)：1419-1425(in Chinese).

［8］ Whipple R T P.Theory of the Spiral Grooved Thrust Bearing with Liquid or Gas Lubricant[M]. Berks：Great Britain Atomic Energy Research Establishment，1951.

［9］ Muijderman E A.Spiral Groove Bearings[M]. New York：Philips Technical Library Springer-Verlag，1966.

［10］ 宋鹏云，陈匡民，董宗玉. 径向直线槽液体机械密封端面间压力分布的数值计算[J]. 四川大学学报：工程科学版，1999，3(2)：122-128.Song Pengyun，Chen Kuangmin，Dong Zongyu. Numerical analysis of the pressure on the face of a radial groove mechanical seal for liquid[J].Journal of Sichuan University：Engineering Science Edition，1999，3(2)：122-128(in Chinese).

［11］ Constantinescu V N，Galetuse S. On extending the narrow sprial groove theory to configurations of interest in seals [J].ASME Journal of Tribology，1992，114(3)：563-566.

［12］ Liu Zhengxian，Wang Musu，Zhou Yue，et al. Dynamic coupling correlation of gas film in dry gas seal with spiral groove[J].Chinese Journal of Mechanical Engineering，2014，27(4)：853-859.

［13］ 黄伟峰，高 志，黎安伟，等. 基于Reynolds方程和基 N-S方程的干气密封性能分析对比[J]. 清华大学学报：自然科学版，2010，50(11)：1820-1824.Huang Weifeng，Gao Zhi，Li Anwei，et al. Comparison between Reynolds equation and Navier-Stokes equa-tion on spiral-groove dry gas seals[J].Journal of Tsinghua University：Science and Technology，2010，50(11)：1820-1824(in Chinese).

［14］ Faria M T C. An efficient finite element procedure for analysis of high-speed spiral groove gas face seals[J].Journal of Tribology，2000，123(1)：205-210.

［15］ Huitric J，Tournerie B. Finite element analysis of grooved gas thrust bearings and grooved gas face seals[J].Journal of Tribology，1993，115(3)：348-354.

［16］ Ruan B. Finite element analysis of the spiral groove gas face seal at the slow speed and the low pressure conditions—slip flow consideration[J].Tribology Transactions，2000，43(3)：411-418.

［17］ 刘正先，周 越. 双向干气密封气膜运行特性的数值分析[J]. 工程热物理学报，2013，34(8)：1466-1469.Liu Zhengxian，Zhou Yue. Numerical analysis of gas seal dynamic characteristics in bi-direction dry gas seal[J].Journal of Engineering Thermophysics，2013，34(8)：1466-1469(in Chinese).

［18］ 徐 洁，谷传纲，王 彤，等. 干气密封三维微间隙流场数值模拟[J]. 工程热物理学报，2007，28(1)：55-57.Xu Jie，Gu Chuangang，Wang Tong，et al. Numerical simulation of 3D flow in spiral groove gas seal[J].Journal of Engineering Thermophysics，2007，28(1)：55-57(in Chinese).

［19］ 冯向忠，彭旭东. 螺旋槽干式气体端面密封的刚度和泄漏量研究[J]. 石油大学学报：自然科学版，2005，29(2)：83-85.Feng Xiangzhong，Peng Xudong. Study of stiffness and leakage rat e of spiral groove dry gas face seals[J].Journal of the University of Petroleum，China，2005，29(2)：83-85(in Chinese).

［20］ 丁雪兴，蒲军军，韩明君，等. 基于二阶滑移边界的螺旋槽干气密封气膜刚度计算与分析[J]. 机械工程学报，2011，47(23)：119-124.Ding Xuexing，Pu Junjun，Han Mingjun，et al. Calculation and analysis of gas film stiffness in the spiral groove gas seal based on the second order slip boundary[J].Journal of Mechanical Engineering，2011，47(23)：119-124(in Chinese).

［21］ 丁雪兴，刘 勇，张伟政，等. 螺旋槽干气密封微尺度气膜的温度场计算[J]. 化工学报，2014，65(4)：1353-1358.Ding Xuexing，Liu Yong，Zhang Weizheng，et al.Calculation of temperature field of micro-scale gas film in spiral groove dry gas seal[J].Journal of Chemical Industry and Engineering，2014，65(4)：1353-1358(in Chinese).

［22］ 彭旭东，谭丽丽，盛颂恩，等. 带内环槽的螺旋槽干式气体端面密封的静压性能[J]. 摩擦学学报，2008，28(6)：507-511.Peng Xudong，Tan Lili，Sheng Song’en，et al. Static analysis of a spiral groove dry gas seal with an inner annular groove[J].Tribology，2008，28(6)：507-511(in Chinese).

［23］ 彭旭东，黄 莉，白少先，等. 雁型槽干式气体端面密封性能的数值分析[J]. 化工学报，2010，61(12)：3193-3199.Peng Xudong，Huang Li，Bai Shaoxian，et al. Numerical analysis of sealing performance of dry gas seal with goose-grooves[J].Journal of Chemical Industry and Engineering，2010，61(12)：3193-3199(in Chinese).

［24］ 周 恒，刘延柱. 气体动压轴承的原理及计算[M].北京：国防工业出版社，1981.Zhou Heng，Liu Yanzhu.The Principle and Calculation of Gas Dynamic Pressure Bearing[M]. Beijing：National Defense Industry Press，1981(in Chinese).

［25］ 曾绍标，熊洪允，毛云英. 应用数学基础[M]. 天津：天津大学出版社，2004.Zeng Shaobiao，Xiong Hongyun，Mao Yunying.Fundamental of the Applied Mathematics[M]. Tianjin：Tianjin University Press，2004(in Chinese).

［26］ Liao X，Yan X，Xia W，et al. A fast optimal Latin hypercube design for Gaussian process regression modeling[C]//Third International Workshop on Advanced Computational Intelligence. Suzhou，China，2010：474-479.

［27］ Park J S. Optimal Latin-hypercube designs for computer experiments[J].Journal of Statistical Planning & Inference，1994，39(1)：95-111.

［28］ Jin R，Chen W，Sudjianto A. An efficient algorithm for constructing optimal design of computer experiments[J].Journal of Statistical Planning and Inference，2005，134(1)：268-287.