一种面向多点定位的协同定位算法
沈家庆,姜维
(中国民航飞行学院航空工程学院,广汉 618307)
0 引言
随着中国经济的增长,航空运输业也得到了快速的发展,为保证航空运输的安全,工业界和学术界对新型监控技术的研究力度也在不断加深。多点定位技术[1]是通过在地面上布置多个地面基站来同时接收同一目标发出的信号,利用不同地面站接收到信号的时间差(TDOA)和接收角度(AOA)来对目标进行精确定位。根据目标到达两个地面站的时间差可绘制一条以两个地面站为焦点的双曲线,目标位置就在这条双曲线上。当有三个地面站时,就能绘制另外两条双曲线来确定目标在平面上的唯一位置。从理论上讲,只要有四个地面站,就可以在空间上确定一点,在实际中就可以投入应用。但在一般的实际应用中都会布置四个以上的地方站以此来减少定位误差,提高对监控目标定位的精确度。多点定位系统具有成本低、精度高、易维护等一系列优点,在国内外已经得到了广泛的应用。因此,对多点定位技术特别是对其定位算法的研究具有极其深刻的意义。
现有关于多点定位所运用的算法有很多且大多数都是基于TDOA的[2],Taylor级数展开法[3]是最经典的一种通过迭代来解决关于TDOA代数非线性问题的方法,迭代过程中每一步都是沿着当前点函数值下降方向。这种方法需要一个初始的预测值,然后通过求解局部线性最小二乘解来一步步的提高估计值的准确性。由于初始值的存在,这种方法也存在着一定的局限性,如果初始值与真实值距离过大,在操作中就不能保证迭代的收敛性,甚至可能会发散导致得不到所要求的结果。因为展开式每一步都要通过最小二乘法来求解,在实际计算过程中的计算量也是非常巨大的。而另外一种经典的Chan算法[4]的计算量就要小很多,是较优的求解双曲线递归方程的方法。Chan算法只需要两步迭代就可以得到最终结果,但如果其定位基站位置和TDOA定位精度存在较大误差的情况下,其定位能力会受到较大影响。针对这个问题,本文利用误差上限,利用文献[5,6]提到的方法,解伪线性方程组,得到定位点的几何位置以及它的斜距,再利用位置斜距的相关性,在定位点几何位置的二范数、斜距相等的条件下,从而获得一个相对误差最小的定位解。再将此定位解作为初值代入Taylor级数展开,可得到一个精确度较高且稳定的结果。
1 误差上限法和Taylor级数展开法介绍
1.1 误差上限法
假设估计目标物体的所在位置m=[x,y,z]T,地面接收站位置,i=1,2,3,4…,N(N≥6),地面接收站i与目标距离为ri,ri=‖ni-m ‖,地面接收站i与地面站1距离为为TDOA 的测量值,c为光速,由空间定位可得:

即:
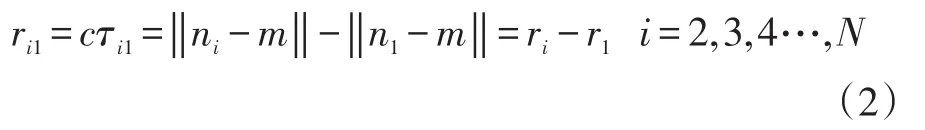
又因为:
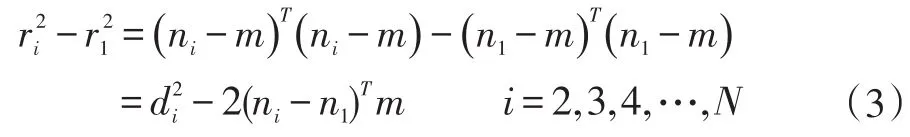
由式(2)式(3)可以得到:

将(4)改成矩阵形式:

其中:
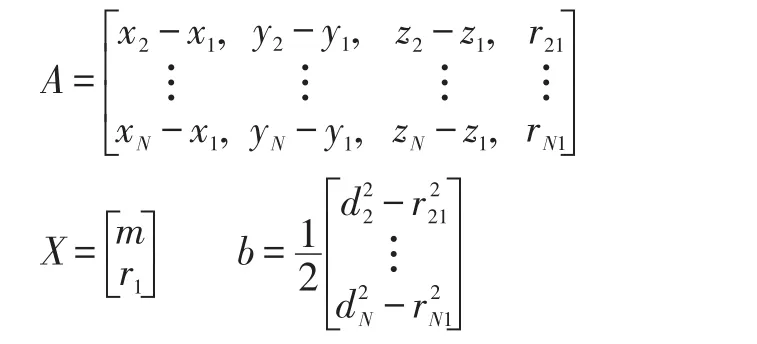
A,b中都含有噪声,在TDOA测量误差或布站误差(布站误差是指第i个基站相对于原点的距离偏差)较大的情况下,以往定位方法的定位精度都有待提高。可以根据布站情况估计其布站误差上限εA和测量误差上限εb,令:
A0=A+δA,b0=b+δb
其中 A,b为测量值,δA,δb为误差,A0,b0为真实值,我们可以得到
(‖x‖2为x的二范数)。
为了求出以上条件的解,首先需要求解:

根据文献[5-6],将(6)转化为:

令A的SVD分解为:

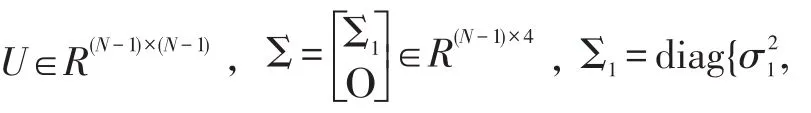

求出定位解:

其中为方程的正根。
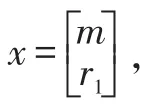
由于噪声的存在,上述等式没有严格成立。可以选择在噪声干扰最小的条件下求得最精确的定位解。可得下式:

由于α为加权系数,可以利用拉格朗日算子来进行计算(10)。
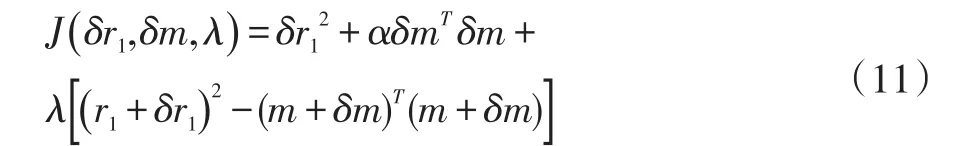
结果为:

其中,α不等于-1。
最终定位。
1.2 Taylor级数展开法
利用Taylor级数展开法计算,首先猜测目标位置为(xv,yv,zv) ,有 x=xv+ δx,y=yv+δy,z=zv+δz。 δx,δy,δz为估计误差。用 Taylor级数令 fi等于(12)
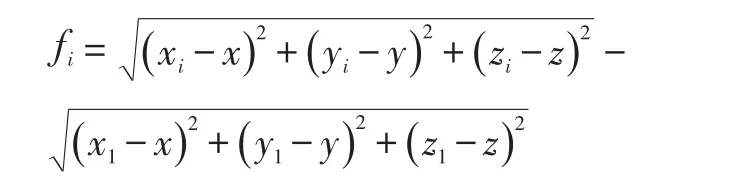
在猜测位置( )xv,yv,zv线性化,得到:

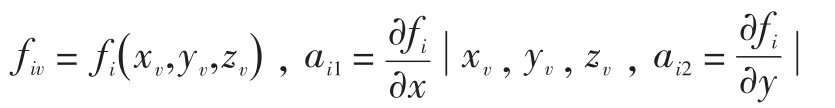
再定义矩阵 M,δ,Z,e:
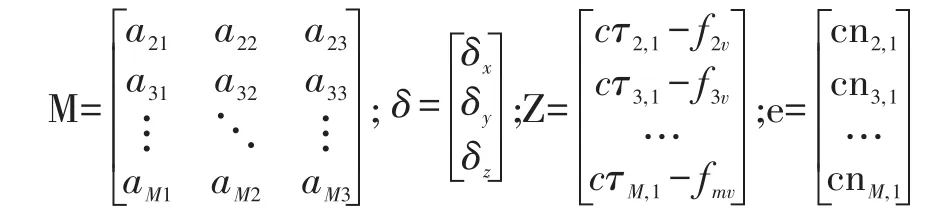
其中M为猜测误差的权,δ为猜测误差,Z为猜测位置观测函数值与实际值的误差,e为测量误差。
则公式可近似表达为Mδ≅Z-e,该公式的转变主要是将对初始位置猜测的误差值并入了测量误差之中,目标位置未知,由此猜测xv,yv,zv,M,Z可以估算,δ,e无法估算 。因为有 x=xv+δx,y=yv+δy,z=zv+δz,设定一个阈值ε,当丨δx丨+丨δy丨+丨δz丨<ε时,可近似认为猜测位置为目标的真实位置。
2 协同算法
虽然Taylor算法的迭代求解计算量相对较小,但由于其计算初始值的存在,如果估测值与真实值误差过大会导致整个算法发散从而得不到结果。本文提出一种新的协同算法能有效地规避这种情况,提高最终定位结果的精确度。首先根据式:

计算求得误差上限法得到的初始定位点,然后将作为Taylor算法所需要的初始值代入式:
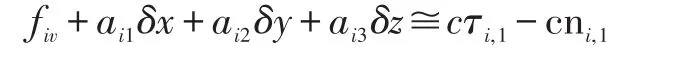
进行展开,通过Taylor算法迭代计算出最终的计算结果。图1为本文提出的协同算法的计算流程图。

图1 协同算法计算流程图
3 仿真分析
为了比较协同算法与其他算法的计算精度,假设六个站的地址为(0km,0km,0km),(9.08km,7.02km,3km),(-9.08km,7.02km,3km),(12.18km,16.06km,3km),(12,18km,-16.06km,3km),(10km,5km,10km)。测量目标的位置为(3km,6km,9km)。在使用MATLAB对协同算法进行仿真后,3种算法在标准相对误差情况下定位精度误差情况比较如图2所示,从图中可以看出,泰勒级数展开法的精度是相比较最低的,协同定位算法的精度比泰勒级数展开法和误差上限法的精度都有了明显的提高。

图2 算法定位精度仿真图
4 结语
以往的定位算法为了能够简单快速地计算出结果而忽略了许多误差的存在,所以导致了最后计算出来的结果与真实值之间存在较大的误差,本文提出的协同定位算法,在计算中引入了测量误差和选址误差并通过利用误差上限对误差大小的控制,减小了计算结果与真实值之间的差距,在通过与Taylor算法的优劣互补,相互协同计算工作,从结果上看进一步提高其定位精度,具有一定的应用价值。但文中方法的缺点也比较明显,由于引进了两项误差并融合了Taylor算法协同计算,用到了矩阵的分解和代数计算,导致计算量相对巨大,在以后的应用中可根据实际要求选择所适合的算法进行计算研究。
参考文献:
[1]Multilateration(MLAT)Concept of use[R].Bangkok:Internatonal Civil Aviation Organization Asia And Pacific Office,2007.
[2]郭华.TDOA定位技术的基本原理和算法[J].西安邮电学院学报,2007(1):19-24.
[3]Foy W H.Position Location Solutions by Taylor Seriesestimation[J].IEEE Trans.on Aerospace and Electronic Systems,1976,12(2):187-194.
[4]Chan,Y.T.Ho,K.C.A Simple and Efficient Estimator for Hyperbolic Location.Signal Processing,IEEE Transactions on,1994,42(8):1905-1915.
[5]Chandrasekaran S,Golub G H,Gu M,Sayed A H.Parameterestimation in the Presence of Bounded Modeling Errors.IEEE Signal Processing,1997,4(7):195-197.
[6]S.Chandrasekaran.Parameter Estimation in the Presence of Bounded Data Uncertainties.Siam Journal on Matrix Analysis&Applications,1998,19(1):235-252.
[7]马广亮.一种用于多点定位系统的实时高精度位置解算方法.科技资讯,2016,14(20):121-124.
[8]王洪,刘昌忠,汪学刚,吴宏刚.一种多点定位的目标位置精确解算方法.航空学报,2011,32(7):1269-1274.
[9]宫峰勋.终端区及场面多点定位中TSOA与TDOA算法性能分析.南京航空航天大学学报,2015;47(6):818-826.
[10]刘刚,赵国庆.时差定位与两种测时差方法[J].电子对抗,2006,20(1):21-25.
[11]汪波,薛磊.基于遗传算法的TDOA定位系统的最优布站算法[J].系统工程与电子技术,2009,31(9):2125-2128.
[12]朱厚庆.到达时间差(TDOA)测向定位研究[J].电讯技术,2007(1):53-56.
[13]毛永毅,李明远,张宝军.基于RBF神经网络的TDOA/AOA定位算法[J].计算机工程,2008,34(2):52-55.
[14]邓平,李莉,范平志.一种TDOA/AOA混合定位算法及其性能分析[J].电波科学学报,2002,17(6):633-636.
[15]俞丽娜,曾连荪,金志华.基于DTOA的无线定位算法研究及精度分析[J].计算机测量与控制,2006(9):1247-1249.

