基于柱面变换的图像拼接技术

杨镇豪

（四川大学计算机学院，成都 610065）

0 引言

伴随着时代的进步和相关计算机技术的发展，现在的人越来越希望用更加便捷、生动的方式与计算机进行交互。虚拟现实技术（Virtual Reality，VR）由于其强大的沉浸感和自然的交互性逐渐成为计算机领域中一个新兴的热点[1]。图像拼接技术是生成虚拟现实全景图的一种关键技术和重要手段，其一般步骤是：将存在一定比例或一定重叠区域的一组或多个图像在空间中进行匹配对准，再多次利用图像融合算法形成全景图。本文着重研究了全景图拼接技术中的投影变换和图像拼接融合等关键技术，分析对比了几种全景图投影变换方法，采用柱面投影算法，解决了全景图像拼接后的视觉一致性的问题，接着使用SIFT特征[2]对图像进行匹配，进行稳定的图像匹配，最后使用利用渐入渐出加权平滑算法图像进行拼接融合，有效地解决了常规加权平均算法中的图像模糊和重影，去除了拼接过程可能产生的拼接痕迹，实现图像的无缝拼接。

1 柱面投影变换

由于摄像机采集的多幅不同视角的图像序列一般不在同一投影平面上，若直接对图像的重叠区域进行拼接融合，会导致融合后的图像场景失去视觉一致性。所以应该先对图像序列进行投影变换之后再进行拼接融合。一般，较为常见的图像投影模型有平面投影、柱面投影、球面投影以及立方体投影等。

平面投影是最简单的投影模型，投影过程中，以图像序列中一幅图像为基准，将其余的图像都投影变换到此坐标系下，由此可以拼接得到平面全景图。但平面全景图的缺点是不能反映空间中的任意方向的场景。球面投影[3]是通过模拟人类视觉特性，将图像序列数据投影到类似眼球的球体上，进而拼接成球面全景图，它可以反映空间中的任意方向的场景，如图1（a）所示。立方体投影[4]与球面投影类似，但它解决了球面投影过程中数据存储困难的问题，图1（b）所示。柱面投影[5]是指建立一个以摄像机焦距为半径的柱面，将图像序列数据投影变换到在此柱面上，然后再经过图像融合过程生成柱面全景图。柱面全景图去除了上方和下方两部分，在水平360度方向为用户提供环形视觉，因此柱面投影相比立方体和球面投影来说容易，又能满足用户的要求，所以被广泛运用。

基于柱面投影变换的图像拼接技术，首先将拍摄得到的原始图像序列映射到一个统一的柱面坐标空间上，即图像的柱面投影变换，然后对图像序列进行图像匹配，计算出两幅图像之间的单应矩阵H，最后根据单应矩阵H和相应的图像融合算法拼接得到全景图。

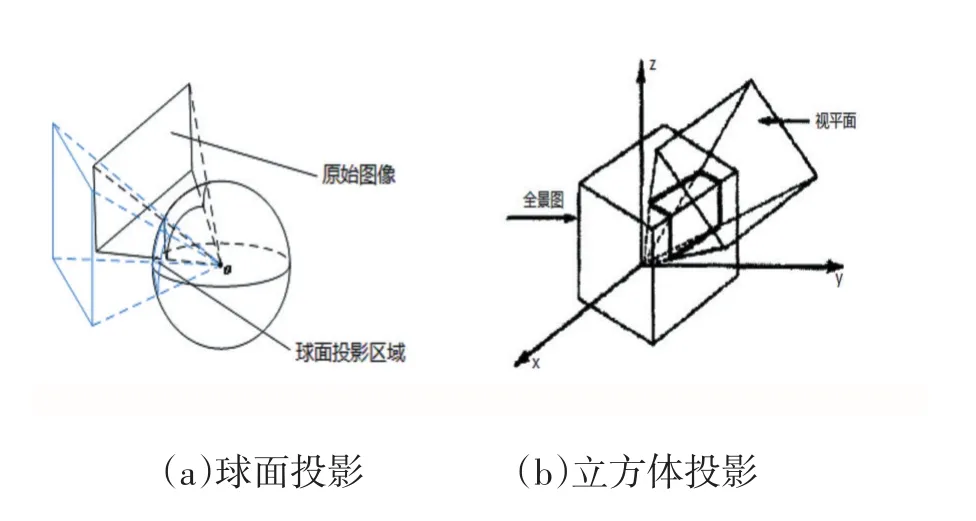
图1 立方体投影与球面投影

投影变换公式是柱面投影变换中最核心的部分，如图2（a）所示，其中原始图像平面用I表示，柱面投影图像使用J表示，K表示柱面投影空间，圆柱中心即投影中心作为坐标原点。如果在x-z平面中进行相机运动，并且光轴和图像平面的交点是图像中心点，现在我们要对原始图像I进行投影变换，得到以O点为观测原点的图像I在投影空间K上的投影J。假设r表示柱面的半径，θ表示投影角，W表示图像宽度，H表示图像的高度，那么可以得到柱面图像宽度为2*r*sin（θ/2）。图像上的像素位置用像素坐标来定义，其中原点为最左上角的像素位置[5]。

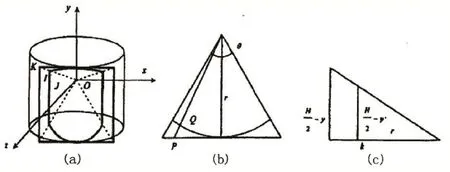
图2 柱面投影变换示意图

假设P为图像I上的随机一点，其坐标为（x,y），现在我们要计算出该点在柱面图像J上所对应的点Q。如果Q点坐标为（x',y'），那么点P对应于y-z平面和x-z平面的横截面分别如图 2（c）和 2（b）所示，这个时候的柱面投影的变化公式为：

那么对于柱面全景图中的任何一个像素点，该点在视线方向θ的反投影图像中的对应点的函数关系可以由正投影方法公式得到，该函数关系如下所示：

2 图像的拼接融合

2.1 平均值融合算法

平均值融合算法是一种简单的线性图像融合算法，它直接把两幅图像的重叠区域按照固定的比例线性累加，而其余不重叠区域不变。设需要融合的参考图像、待配准图像和融合后的图像分别用I1（x,y）、I2（x,y）和I3（x,y）表示，那么实现平均值融合法如下：生成全景图中的一个重要步骤之一就是图像的拼接与融合。图像的拼接是要以两幅图像之间有一定重叠区域为条件的。因为有重叠区域的时候我们才能利用算法去配准这两幅图像。另外，两幅图像之间是需要拥有视觉一致性的。这也是之前我们所说的要进行柱面投影或者运用其他投影模型的原因。目前，比较常用的图像拼接融合算法主要有：平均值融合法、加权平均融合算法与渐入渐出融合算法，下面就分别对这三种算法进行简要的介绍。

其中，R2为参考图像和待配准图像中的重叠区域，R1与R3为各自图像中不重叠的区域。该算法使用的前提是两幅待融合的图像亮度变化不大，然后在图像重叠区域应用不变的权值1/2来合并图像像素值，使参考图像能平滑过渡到待配准图像。平均值融合算法原理简单且易于实现，算法运行效率高；但算法融合效果不稳定且局限性很大，容易受到图像亮度的影响，并且可以很清楚地看到融合后图像的拼接缝隙。

2.2 加权平均融合算法

加权平均融合算法解决了平均值融合算法的缺点，在图像重叠区域使用可变的加权函数来合并图像像素值，使图像的重叠区域融合更加平滑，可以实现像素的逐渐过渡。设待融合图像的重叠区域为{x1，x2}，加权函数为W1（x）和W2（x），它们之间的关系如下：

其中，i的值域为{0，W}，W=x2-x1，因此融合后的图像像素值为：

加权平均融合算法基本上消除了拼接时的模糊和鬼影现象，可以完成重叠区域内像素值之间的平滑过渡。该算法快速简单，是一种比较常用的图像融合算法。根据所使用加权函数的不同，我们可以将加权平均融合算法分为多种不同类别的算法，如帽子函数加权融合算法、渐入渐出融合法等。其中，帽子函数加权融合算法主要考虑了图像中像素距离与权值之间的关系。该算法认为图像像素点距离图像中心越近，其贡献程度越大，即它所对应的权重大，边缘区域占较小的权重。权值函数中width和height两个参数分别表示融合图像的宽和高。在三维空间中，权值函数的函数图类似帽子形状，这也是叫帽子函数加权融合算法的原因。如（6）、（7）式所示:

2.3 渐入渐出融合算法

渐入渐出融合算法[6]是由Szeliski所提出来的，图像重叠区域的权值d是根据该像素点到重叠边界的距离计算出来的，它与像素点位置与边界距离呈现线性关系，由此可以实现图像重叠区域内的平滑过渡。算法的计算公式如（8）、（9）式所示，其中 j为像素点所在的列数，L、R为重叠区域的左、右边界。

3 基于柱面变换的图像拼接算法实现步骤

（1）对原始图像序列进行图像预处理和畸变矫正

在对图像进行拼接之前，需要对原始图像序列进行预处理操作，去除图像中的高频噪声，如椒盐噪声、白噪声、高斯噪声等，一般采用各种类型的图像滤波处理。而畸变是指由于摄像机镜头制造工艺、安装、装配等各种原因导致的图像畸变效果，为了能够提高摄像机拼接的效果和精度，需要对所有图像序列进行畸变校正步骤。

（2）对原始图像序列进行柱面投影变换

在经过图像预处理和畸变矫正步骤后，接下来一步是对需要拼接的图像序列进行柱面投影变换。正如第1节所讨论的，柱面投影变换的目的是为了保持图像重叠区域内景物的视觉一致特性。

（3）对图像序列进行图像匹配，计算两幅图像之间的单应矩阵H

由于SIFT[2,7]（Scale Invariant Feature Transform）特征具有良好的尺度不变性、旋转不变性和亮度不变性，对环境适应性极佳，同时其生成的特征描述符能保证相当高的匹配正确率。因此本文采用SIFT匹配算法得到待拼接图像的匹配对，然后再根据得到的匹配对利用DLT（Direct Linear Transformation，直接线性变换）计算出图像之间的单应矩阵H。

（4）最后根据H矩阵信息利用相应的图像融合算法对图像进行拼接，生成全景图像。

4 实验结果

根据上述算法思路，用MATLAB进行实验仿真，通过摄像机采集的多幅图像，对其进行图像拼接对比实验。下面是其中一组图像，首先图3、4展现了投影角度取为45°的柱面投影图。

图3 原图1及其柱面投影图

图4 原图2及其柱面投影图

接下来展示下平均值融合算法和渐入渐出算法的实验效果，并且进行对比，如图5、6所示。（用来拼接的图像分别已经在上述的图像投影变换中已经展示，都是进行过畸变校正后再进行柱面变换投影的图像）

图5 平均值融合算法示例图

图6 渐入渐出融合算法示例图

我们从上面两幅图中可以明显得看出平均值融合算法和渐入渐出融合算法的效果。我们可以看到图5虽然图像进行了融合，但均存在比较明显的过渡带，而且图5中间融合的效果十分不好，非常模糊。再来观察图6，经过渐入渐出融合算法后，拼接的结果自然，图像重叠区域过渡平滑，基本实现了无缝拼接。

5 结语

针对虚拟现实领域中生成全景图的需求，本文利用柱面投影变换得到图像序列的柱面投影图，然后根据SIFT匹配算法得到待拼接图像之间的匹配关系，采用渐入渐出融合算法对图像进行拼接，得到了图像拼接后的全景图。经过实验仿真证明，该算法能快速、鲁棒的对图像无缝拼接。

参考文献：

[1]苏建明，张续红，胡庆夕.展望虚拟现实技术[J].计算机仿真，2004，21（1）：18-21.

[2]DG Lowe.Distinctive Image Features from Scale-Invariant Keypoints.International Journal of Computer Vision,2004,60（2）:91-110.

[3]杨燕，王雪瑞，戴青，付江柳.球面全景图像生成技术的研究[J].计算机应用与软件，2007，24(10）：164-165.

[4]韦群,高丽,龚雪晶.基于立方体全景图的虚拟场景浏览技术研究及实现[J].中国图象图形学报,2003,8（9):1061-1066.

[5]杨艳伟，郭宝龙.柱面全景图像自动拼接算法[J].计算机工程与应用，2009,45(9):171-173.

[6]卢斌，宋夫华.基于改进SIFT算法的视频图像序列自动拼接[J].测绘科学,2013,38(1):23-25.

[7]Szeliski R.Image Mosaicing for Telereality Applications.IEEE Computer Graphics and Applications，1994.